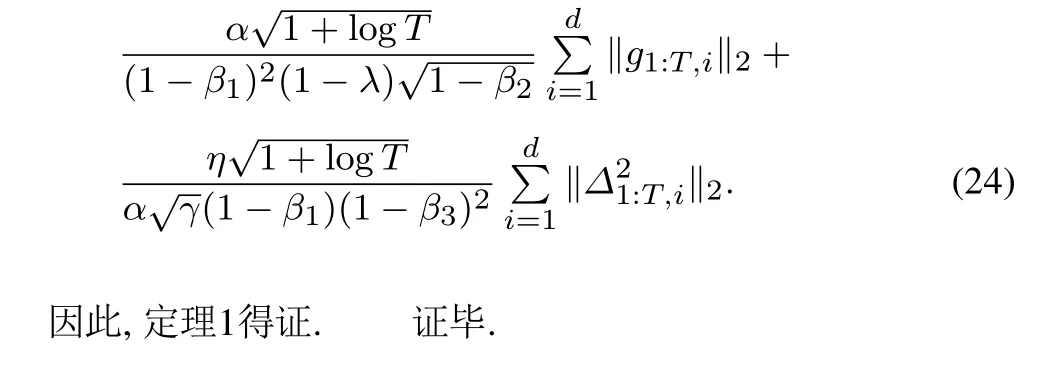带有微分项改进的自适应梯度下降优化算法
2022-05-21葛泉波张建朝杨秦敏
葛泉波 ,张建朝 ,杨秦敏 ,李 宏
(1.南京信息工程大学自动化学院,江苏南京,210044;2.杭州电子科技大学自动化学院,浙江杭州 310018;3.浙江大学控制科学与工程学院,浙江杭州 310063;4.中国飞行试验研究院,陕西西安 710089)
1 引言
BP(back propagation)神经网络,其计算过程由正向和反向过程组成,广泛应用于如图像分类[1-2]、目标检测[3]和人脸识别[4]等领域,其能否成功的关键因素为网络的泛化能力.虽然BP神经网络在人工智能领域取得了巨大的成功,但是面对越来越庞大的数据集,进行深度网络的训练需要消耗巨大的计算成本,即使使用高配置的GPU服务器也需花费较长的训练时间.因此,在不牺牲甚至提高准确率的基础上,尽可能地加快深度网络模型的训练速度尤为重要.这样不仅可以节省训练时间,也可以节约硬件设备的成本[5].BP神经网络的性能主要取决于其网络结构与优化算法.对于一个神经网络结构,其全部信息主要体现在网络连接权重的分布上,网络权重直接影响了BP神经网络的收敛速度与精度.优化学习算法作为修正权重的关键,决定着BP神经网络性能优劣.
目前,大多数的优化算法是基于迭代的方法,该类方法通过迭代优化辅助目标函数,向着最优解决方案寻找一组参数(即权重)[6-8],主要使用的算法是基于随机梯度下降(stochastic gradient descent,SGD)的改进算法.SGD动量策略是同时考虑过去和现在的梯度来更新网络参数,但该方法存在超调问题,即权值超过最优解而不改变更新方向的现象[9].这种超调问题阻碍了SGD动量的收敛,耗费了更多的训练时间和资源.在自动控制文献[10-11]中,梯度优化算法与传统控制有相似之处.在反馈控制系统中比例积分微分(proportional integral derivative,PID)控制器[12-13]由于其简单、功能和广泛的适用性,是最常用的反馈控制机制.其控制的基本思想是控制动作应与当前误差(系统输出与期望输出之差)、过去误差(积分)、未来误差(导数)成正比.文献[14]指出,自适应机制通过利用移动平均梯度和移动平均平方梯度来计算自适应指数衰减速率,实现自适应学习率,这种自适应调整方式有很大优势,并且有望产生更好的深层模型学习结果.
学习率是训练深度神经网络(deep neural networks,DNN)最重要的超参数之一,其选择的合适与否直接影响网络优化的好坏.根据学习率的设置,深度学习优化器可以分为两类:手动调整的学习率优化器,如SGD[15]、SGD动量和Nesterovs动量[16],以及自适应学习率优化器,比如AdaGrad[17]、RMSProp[18]和Adam[19]等.目前优化算法的主要思想是根据神经网络特性修改学习率,从而改进学习率太小而导致缓慢的收敛速度,而学习率太大影响收敛速度.因此优化学习的稳定性取决于超参数的选择,而且配置学习算法的超参数的方法是层出不穷的,需要手动调整敏感的超参数,通过调优阶段以获得预期的理想性能.然而这种调优需要非常昂贵的人力和时间资源,每个超参数的设置通常需要在多个阶段进行多次测试[20].
为了解决该问题,首先结合传统PID原理,对SGD进行重整合,通过分析得出梯度的累积类似于PI控制,而积分环节使得梯度更新受到历史梯度影响,因此出现较大超调量.通过结合传统控制理论的微分环节校正思想,在迭代过程引入微分项,从而有效提高算法对于瞬时梯度改变的灵敏度,有效改善了权重更新滞后于实际梯度改变的缺点.在此基础上,通过引入指数衰减的历史平方梯度及历史梯度的指数衰减值来实现学习率自适应改变,有效地解决了固定学习率导致算法收敛速率过慢的问题.最后结合指数加权移动平均法,进一步克服了迭代初始阶段较大误差的问题.
2 背景和研究动机
2.1 卷积神经网络
卷积神经网络(convolutional neural networks,CNN)是基于前馈神经网络的深层神经网[2,9-10,21].CNN的三大特性,即局部感知、权值共享及降采样显著减少了网络的参数,大大降低了训练网络的计算复杂度,这也决定了CNN的在数据处理的优越性,使得CNN在手写体识别、图像分类等深度学习领域得到广泛应用,成为计算机视觉系统的核心技术.
卷积运算实际上是对图像的矩阵运算,通过卷积核与输入数据一部分进行卷积运算,提取出该部分的特征.卷积公式如下[21]:

从图1可以看出,在神经网络训练模型中,反向传播类似于控制系统的反馈环节,梯度相当于误差,实际标签值相当于理想值,控制系统的目标是连续测量输出系统的状态,并通过控制单元将其更新到所需的状态.而神经网络模型是学习一个能够描述输出输入关系的近似函数,两者具有相似性.
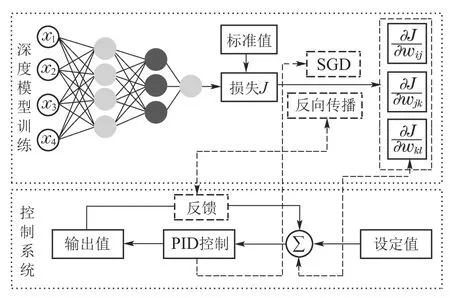
图1 神经网络训练模型与控制系统联系[9]Fig.1 The connection between neural network training model and control system[9]
2.2 梯度优化算法
在卷积神经网络中,为了得到最优的权值,需对模型创建代价损失函数,然后选择合适的优化算法使损失函数值最小,其形式化描述如下[22]:
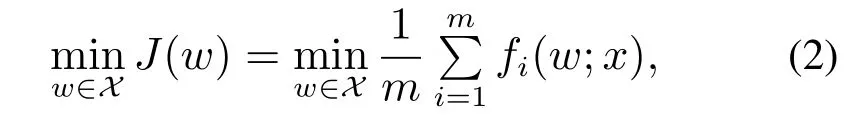
其中:m表示样本数,fi(w;x)表示单个样本i的损失函数,X表示约束集.在卷积神经网络的训练问题中,损失函数fi(w;x)可定义为[14]
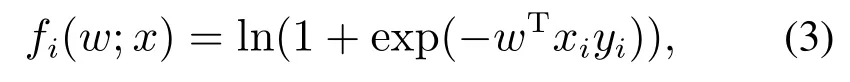
其中:(xi,yi)是训练样本序列,x为单个样本xi的集合.为了求解问题(2),随机梯度下降法是最常用的方法,它的更新规则如下[19]:
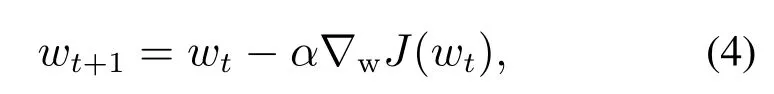
其中:α表示学习率,∇wJ(wt)为函数J(w)在wt上的梯度值.上面算法与PID控制输入输出公式对比,可以看出都是利用了当前信息更新,相当于比例环节.如果更新的权重如果要改变下降的方向,由于历史梯度累积的存在,权重将不会及时改变[11],这一现象通常被称作超调.
2.3 研究动机
目前,在神经网络训练中常用的优化算法主要是SGD算法及其改进,在实际应用中也取得了比较不错的成绩.然而,这种基于迭代的优化方法在实际应用中也存在许多的问题[9-10].
1) 传统基于SGD的优化算法中出现过大的超调量将导致收敛过程频繁震荡,影响算法收敛速率.该类方法主要考虑利用过去和现在的梯度来更新网络参数,历史梯度值的累积过程容易造成权重的值超过其目标值的现象,并且可能不会改变更新方向,因此阻碍算法收敛,耗费巨大的训练时间.
2) 在稀疏特征处理过程中,固定学习率的机制将严重影响优化算法的收敛速率.学习率作为BP网络重要参数,其适合与否直接决定网络优劣,而目前主要以手动调节为主,该方式在大型网络操作难度较大且固定学习率对于网络适应性较差,即当权重参数远离最优点,希望调大学习率以加快训练,而当离最优点较近时则希望调小学习率以提高精度.
因此,在研究如何有效克服迭代过程出现超调量问题的基础上,进一步有效应用自适应学习率对于进一步提高优化算法的收敛速率有很大必要性.对此,本文提出的解决方案如下:
1) 结合传统控制系统原理,引入微分环节来解决随机梯度下降算法存在超调问题.微分环节通过有效利用当前时刻梯度的瞬时变化率校正梯度更新,从而保证梯度随着迭代进行而单调收敛到最优值.
2) 针对学习率的不适应性导致的收敛率差和收敛速率慢等问题,提出一种基于二阶矩的自适应学习率机制.该机制主要通过将过去平方梯度(二阶矩)的平均值和过去梯度的指数衰减平均值添加到学习率调节过程中,以此来增强学习率的自适应性并提高相应的收敛速率,同时给出了相应的悔界证明.
结合上述问题分析,本文所提出的带微分项的自适应梯度下降法流程如下图所示.
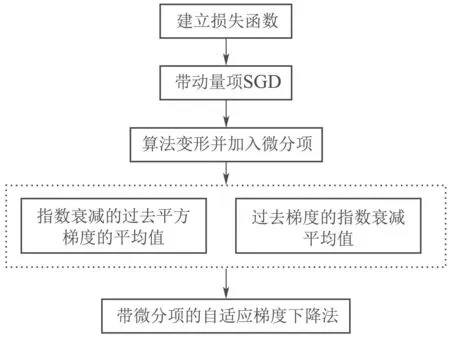
图2 算法框图Fig.2 Algorithm block diagram
3 问题描述与算法设计
3.1 问题描述
在完全信息反馈设置中,在线优化问题是一个分析迭代优化方法的灵活框架.在线问题可描述如下:在每一轮t,优化算法选择一个动作wt ∈X,其中X⊂Rd,则遭受的损失为J(wt).因此,经过T轮之后,算法的悔函数可定义为[22]

3.2 算法设计
为了快速训练深度神经网络模型,本文结合自适应梯度算法和PID原理的优势,提出一个带微分项的自适应梯度优化算法(adaptive stochastic gradient descent with differential,AdaSGD-D),具体描述如下:在每一轮t ∈{1,···,T}[19],

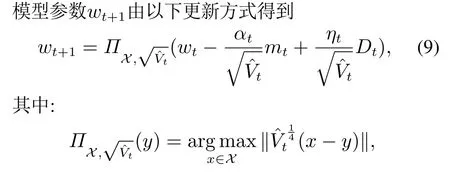
αt为学习率,ηt表示微分步长.与文献[19,22]中的更新规则相比,式(9)给出的模型参数更新规则增加了跟Dt相关的一项,它能有效地提高模型的训练速度.
本文提出的AdaSGD-D算法流程参见算法1.
算法1带微分项的自适应梯度下降法(AdaSGD-D).

4 性能分析
对AdaSGD-D算法的悔界分析,是一个非常重要的工作,它能从理论上保证新算法的收敛性和收敛速度,以提高算法的工程可用性.为了完成本文算法的悔界分析,需要如下标准假设[22]:


超参数β1t是影响算法收敛性能的一个重要参数.从式(10)右边第2项可以看出,β1t需要满足一定的衰减条件,比如β1t是时间t的一个递减函数[22].因此,获得β1t=β1µt−1条件下定理1的一种具体形式更能够直观地表达悔界结果的内涵,从而可在工程应用过程中超参数取值方面起到良好的指导作用.
与文献[9]相比,本文分析了收敛速率,从理论上保证所提算法是收敛的.文献[9]基于PID原理进行更新,没有采用自适应步长.在悔界的理论分析中,动量的上界与梯度的上界都是G∞,而常步长不影响结论的推导,其分析过程与在线梯度下降算法相似,因此理论上的悔界与在线梯度下降算法的悔界相似,即[25].但是所提算法的悔界可达到O(Tκ)(0 ≤.尤其当梯度是稀疏时(在实际应用中,梯度通常是稀疏的),所提算法的收敛速度比文献[9]更快.由此可知,新算法中引入了自适应学习机制,可利用训练数据的稀疏特征来显著提高深度神经网络的训练速度.与文献[22]的工作相比,新算法采用了基于PID原理的微分环节校正思想,从而可有效改善文献[20]中权重更新滞后于实际梯度改变的缺陷不足.虽然新算法的理论结果在框架上与文献[22]类似,但由于新方法在文献[22]的模型更新基础上增加了一个有效的微分项,从而可起到改善算法收敛性能的作用.同时该微分项的影响也在悔界结果表达式中显示体现.实验结果表明AdaSGD-D的训练性能优于文献[22].目前本文得到的上界可能比较宽松,在未来的工作中将试着推导一个更紧的上界.
5 仿真实验
在本文的仿真实验里,首先在MNIST手写体分类数据集中分别使用所提出的带微分项的自适应梯度优化算法(AdaSGD-D)及传统的带动量的随机梯度下降法(stochastic gradient descent with momentum,SGD-M)[16]、Adam[19]训练了一个简单的多层感知网络,以证明AdaSGD-D的优势;然后在CIFAR-10图像数据集上训练了一个基于卷积神经网络的分类模型,通过结果来证明所提AdaSGD-D算法精度及收敛速率都得到提升及所做工作的必要性.
5.1 数据集
MNIST数据集[13]:MNIST数据集包含60,000手写体的训练样本和10,000个测试样本从0到9的数字.图像为28×28像素,并且以灰度格式显示.如图3所示.

图3 MNIST数据集部分图像Fig.3 Partial images of MNIST dataset
CIFAR-10数据集[22]:包含6万张RGB彩色图像,其形状为32×32.共有10类,每类包括60,000张图像.为了进行训练和测试,将数据集按照5:1的比例进行划分,即训练集使用50,000张,测试集10,000张图像.如图4所示.

图4 CIFAR-10数据集部分图像Fig.4 Partial images of CIFAR-10 dataset
5.2 MNIST数据集下仿真结果
在本小节基于MNIST手写体分类数据集中,分别使用所提出的带微分项的自适应梯度优化算法(Ada-SGD-D)及常规带动量的随机梯度下降法(SGD-M)、Adam训练了一个简单的多层感知网络.多层感知网络使用ReLU非线性激活函数,隐藏层1000个节点,softmax输出层.每批次128张图片,共100轮数.3种优化算法训练统计如下图5-8所示.
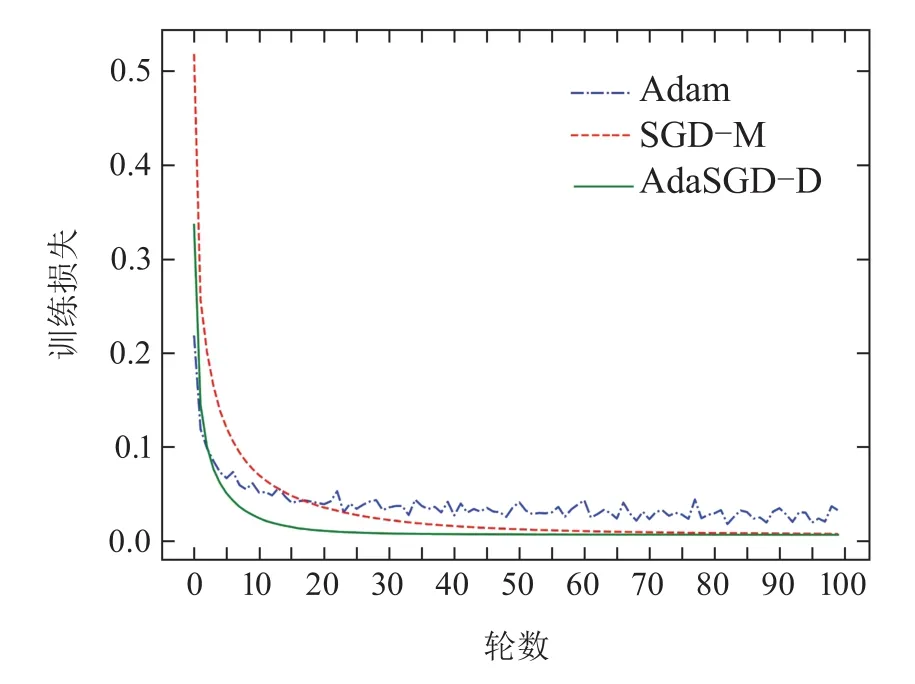
图5 训练损失曲线Fig.5 Training loss curve
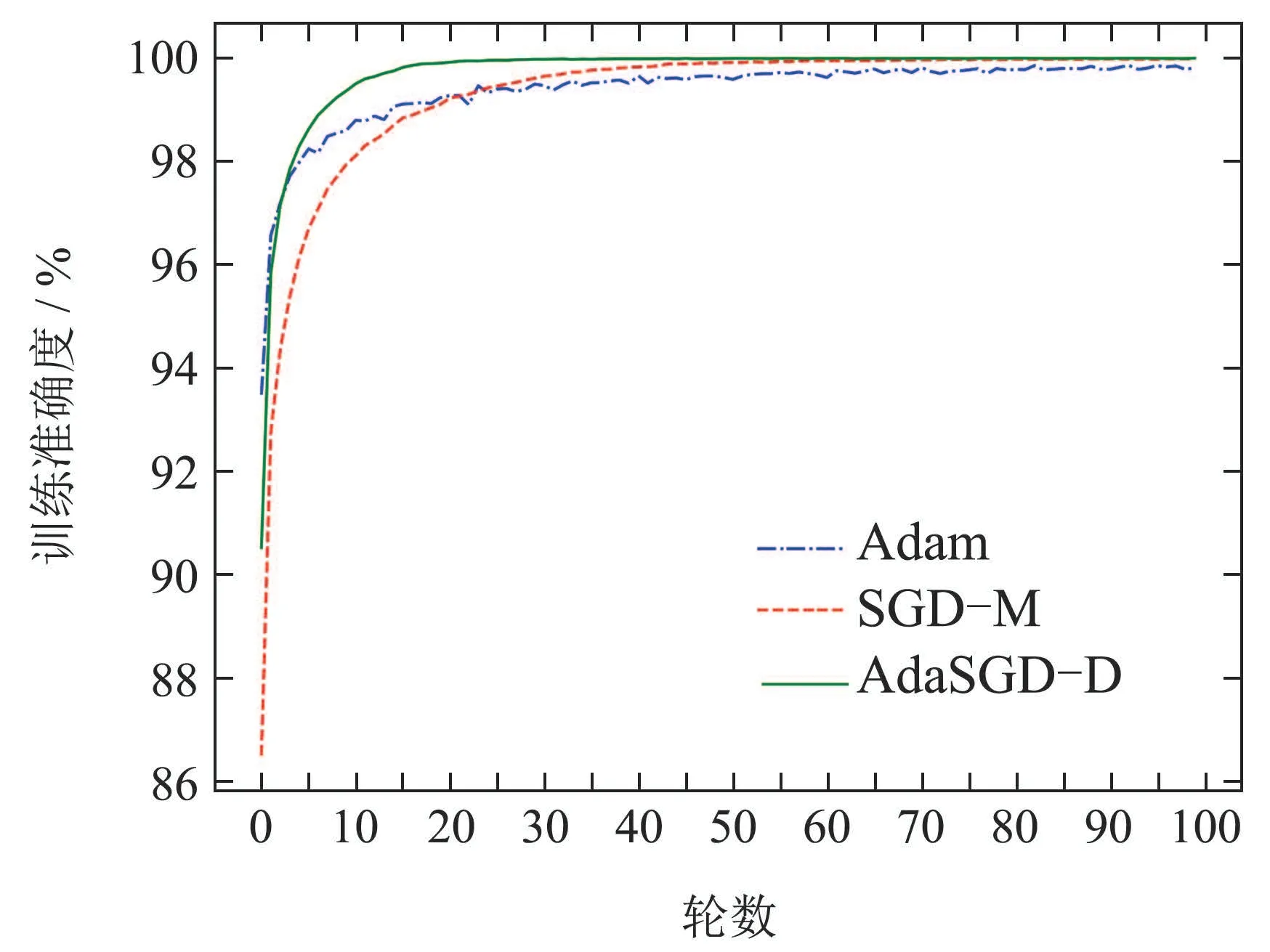
图6 训练准确度曲线Fig.6 Training accuracy curve
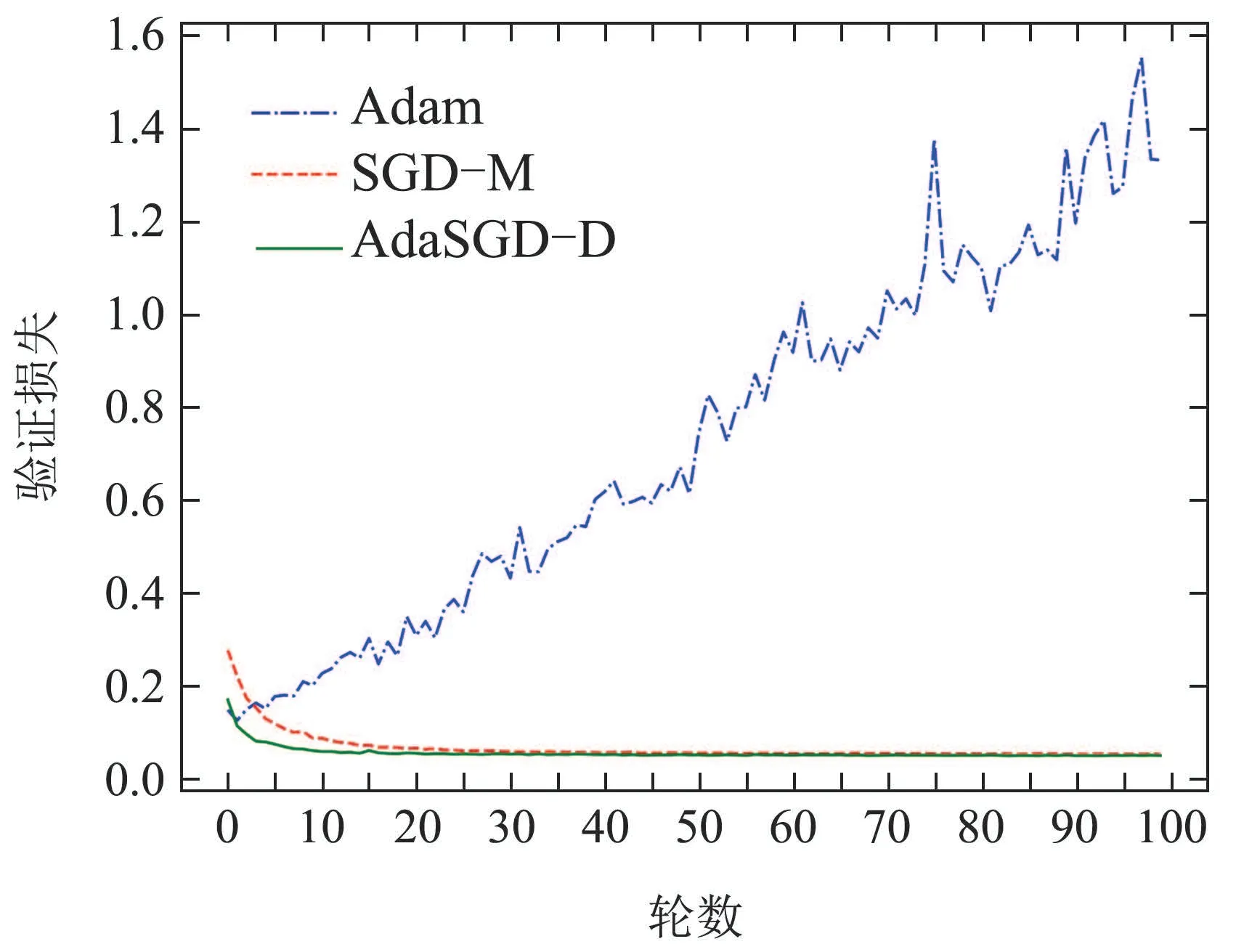
图7 验证损失曲线Fig.7 Verification loss curve
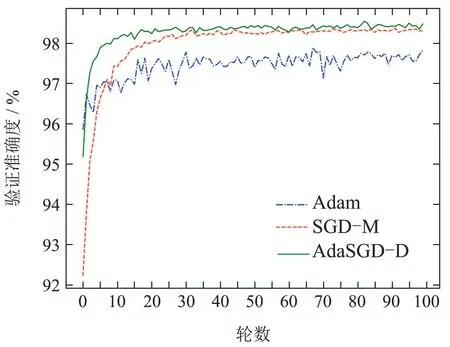
图8 验证准确度曲线Fig.8 Verification accuracy curve
从图5-8中可以得出如下结论:
1) AdaSGD-D算法的训练准确度(在训练集中预测正确的次数与所有预测次数的比值)高于SGD-M和Adam算法.由于AdaSGD-D算法引入了微分项和自适应学习机制,不仅利用了梯度的历史信息,同时也利用梯度的未来信息和当前信息,有效改善了模型训练的速度.在训练MNIST数据集上训练100轮次后进行观察,从第5轮次到第35轮次,AdaSGD-D算法的训练精度可达99.85%,其他两种方法精度大约为97.5%.随着训练轮次的增加,在第50轮次后,AdaSGD-D和SGD-M算法的训练准确度均可达到100%,而Adam算法的训练精度为99.8%.因此,AdaSGD-D算法在模型训练过程初始阶段的训练速度要快于SGD-M和Adam算法;在模型训练过程末尾阶段,训练准确度能达到100%,高于Adam算法.
2) AdaSGD-D算法的验证准确度(在测试集中预测正确的次数与所有预测次数的比值)高于SGD-M和Adam算法.新算法引入了微分项,可利用梯度的未来信息,使得算法的收敛速度加快.自适应学习机制针对测试数据的稀疏特征,自适应调整学习速率以提高测试准确度.在测数据集上测试100轮次后进行观察,AdaSGD-D算法的收敛速度最快,在第15轮次时就可稳定收敛,验证准确度可达98.45%.SGD-M算法的收敛速度次之,在第35轮次时才逐渐收敛,验证准确度为98.28%.Adam算法收敛速度最慢,在第40轮次左右才逐渐收敛,验证准确度为97.65%.因此,AdaSGD-D算法在模型验证过程中的验证准确度都优于SGD-M和Adam算法,而且AdaSGD-D的验证准确度比Adam算法高出近1%.
5.3 CIFAR-10数据集下仿真结果
在本小节中,利用CIFAR-10图像数据集中的数据训练了一个基于ResNet18[23]的图像分类器,其中梯度优化算法分别使用了所提出的基于带微分项的自适应梯度优化算法(AdaSGD-D)及传统带动量的随机梯度下降法(SGD-M)和Adam自适应梯度优化算法,3种优化算法的性能如图9-12所示.
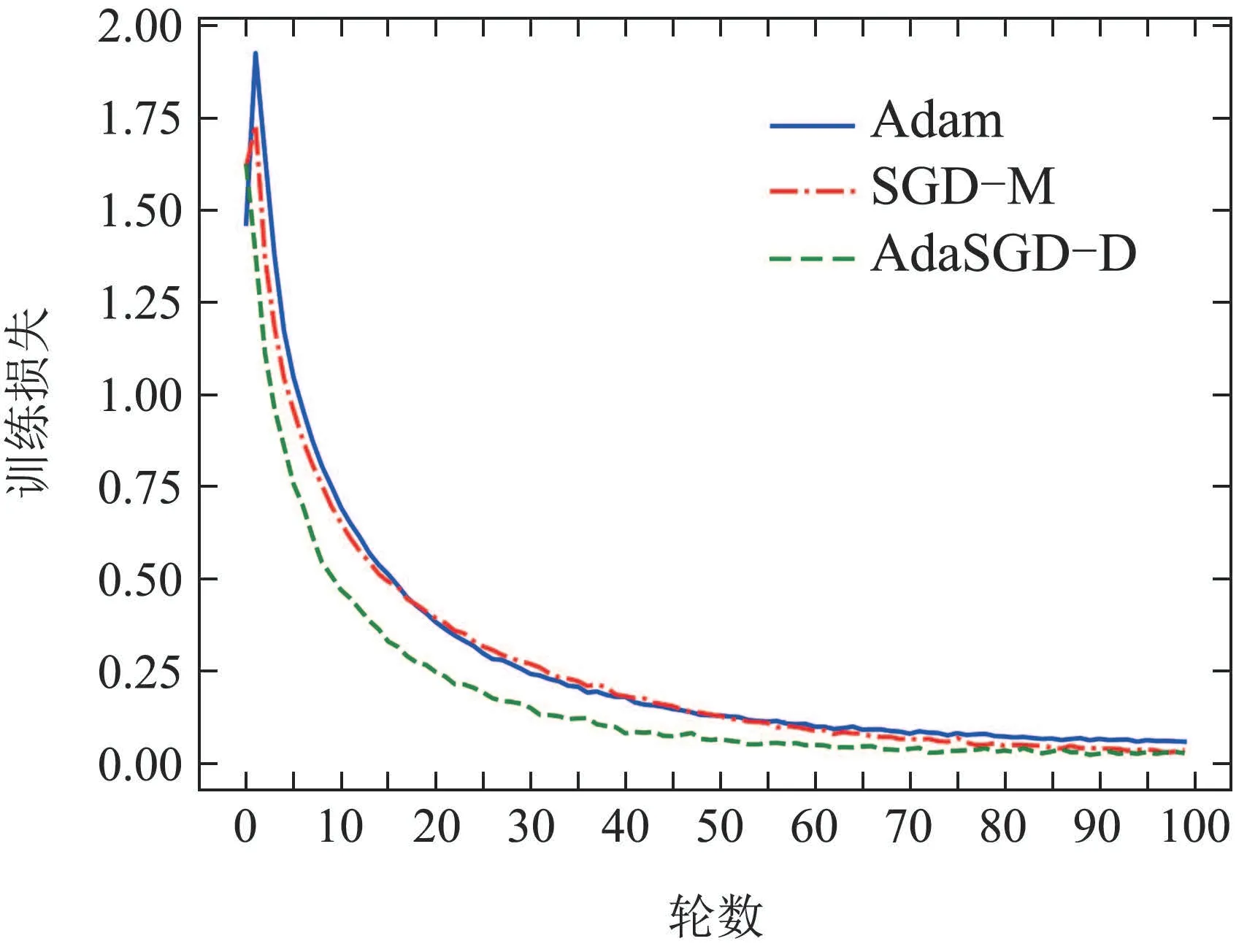
图9 训练损失曲线Fig.9 Training loss curve
从图9-12中可以得出如下结论:
1) AdaSGD-D算法的训练准确度高于SGD-M和Adam算法.由于微分项和自适应学习机制的引入,AdaSGD-D算法同时利用了梯度的历史信息,当前信息和未来信息,有效改善了模型训练的速度.在训练数据集上训练100轮次后进行观察,AdaSGD-D算法的收敛速度最快,在第55轮左右训练的精度可达99.13%,而Adam和SGD-M算法在80轮之后才达到稳定收敛,此时SGD-M的训练精度为99%,Adam的训练精度大约在98.63%.随着训练轮次的增加,在第85轮次后,所有方法的训练准确度均可达到100%.因此,新算法在模型训练过程初始阶段的速度快于SGD-M和Adam算法;在模型训练过程末尾阶段,训练准确度也优于SGD-M和Adam算法.
2) AdaSGD-D算法的验证准确度高于SGD-M和Adam算法.AdaSGD-D算法引入了微分项,可利用梯度的未来信息,加快算法的收敛速度.同时采用了自适应学习机制,针对测试数据的稀疏性,自适应调整学习速率来提高测试准确度.在测试数据集上,测试100轮次后进行观察,AdaSGD-D,SGD-M和Adam算法均在第50轮次后达到稳定收敛,AdaSGD-D的测试准确度最高,可达到91.52%,SGD-M算法次之,其测试准确度可达到88.96%,Adam算法的测试准确度最低,为88.47%.因此,AdaSGD-D算法在模型验证过程中的准确度都优于SGD-M和Adam算法,而且在模型验证的末尾阶段,AdaSGD-D算法的验证准确度比SGD-M算法高出2.56%,比Adam算法高出3.05%.
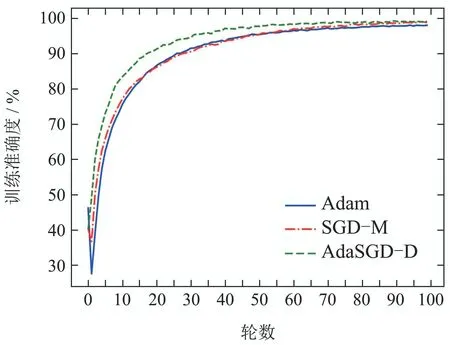
图10 训练准确度曲线Fig.10 Training accuracy curve
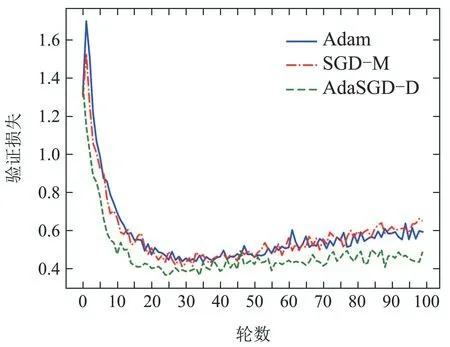
图11 验证损失曲线Fig.11 Verification loss curve
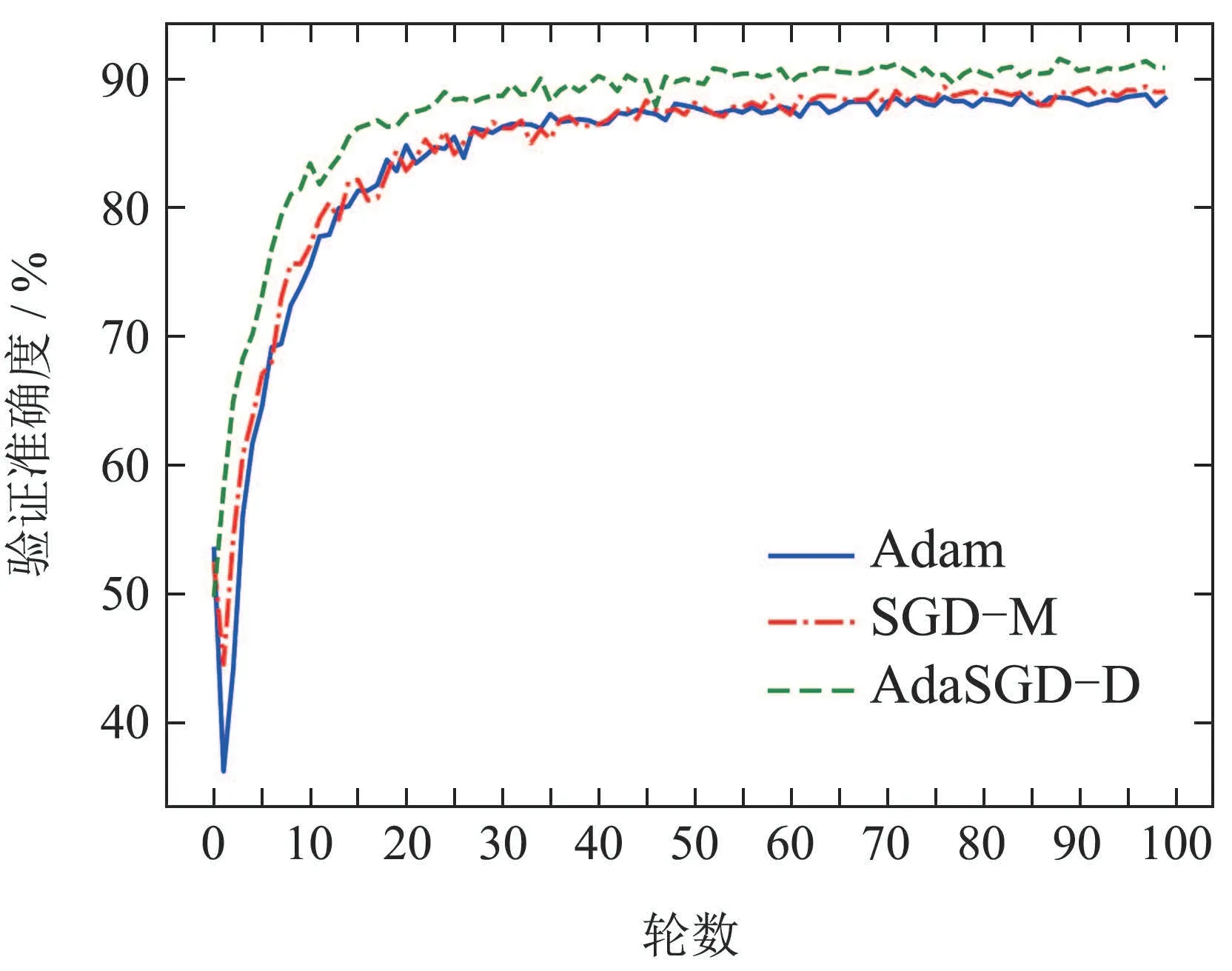
图12 验证准确度曲线Fig.12 Verification accuracy curve
6 结论
针对大规模神经网络优化收敛速率慢、权重更新滞后于实际梯度改变及固定学习率无法适应训练过程的问题,本文提出了一种带微分项的自适应梯度优化算法.首先,重新整合了传统的随机梯度下降算法,并结合传统控制论思想,引入微分项,有效解决权重更新滞后于实际梯度问题;其次,本论文加入了自适应调节机制,通过引入过去平方梯度值,对学习率进行自适应调整;然后利用过去梯度的指数衰减平均值并引入偏差校正,有效地实现了动态调节学习率,进一步提高了神经网络的训练速率.
附录
定理1的证明:参照文献[22]的证明思路.根据wt+1的更新规则有