非完整约束多智能体系统基于屏障控制函数的分布式协同控制
2022-05-21娜茜泰夏元清
娜茜泰 ,高 飞 ,翁 智 ,夏元清
(1.内蒙古大学电子信息工程学院,内蒙古呼和浩特 010021;2.北京理工大学自动化学院,北京 100081)
1 引言
多智能体系统是分布式人工智能的一个重要分支.随着人工智能、机器人技术、计算机科学、集成技术等多学科多领域的交叉融合与发展,多智能体技术的研究与应用也达到了前所未有的高度.2019年爆发了新型冠状病毒引起的肺炎疫情,促使无人系统往各个民用领域快速渗透,例如无接触货运物流系统、无接触物资分发系统等,都更大程度的开始依赖无人系统来解决[1-2].这些刻不容缓的需求和任务,极大地反映了当前无人化产业所面临的考验和迫切需要解决的问题.这些无人化系统,也就是常说的机器人、智能体,必须具备独立的感知、决策、通信,以及执行能力,才能可靠地实现相应的任务和需求.例如智能物流分拣车,需要多车配合完成物资的分发,其中就涉及到任务的分配和计算.再比如日常的巡逻作业,需要多车之间的队形保持和相互之间的通信保持.上述内容都是多智能体系统非常重要的研究分支.
本文主要研究内容集中在多智能体协同控制的编队和连通性保持方面.在现有很多连通性保持协同控制算法中,代数图论是多智能体一致性、编队和连通性问题的应用最广泛的研究方法之一.通过将通信关系建模为有向图或无向图,将智能体与其邻居之间的相对信息作为控制变量,分析通信拓扑图拉普拉斯矩阵的特征根来判断能否达到期望的稳定队形[3].或者利用集中式或分布式优化方法,使拓扑图的代数连通度始终为正,便可有效实现系统的拓扑连通性保持.这类方法非常适合线性系统基于图论的队形稳定性和连通性的控制器设计.而对于非线性系统,往往采用基于李雅普诺夫函数的方法.
不同于利用拓扑图的代数连通度来控制连通性的方法,本文采用基于屏障控制函数(control barrier function,CBF或栅栏函数[4])的控制器设计方法.早期,Sontag等[5]针对屏障函数(barrier function,BF) 和李雅普诺夫函数的相关性进行了研究,后来逐渐被引入到有反馈的控制系统中,演化出屏障控制函数的概念[6].屏障控制函数可解决有系统约束或状态约束的问题,将系统输入与状态约束转化为屏障控制函数,并对其导数引入不等式约束,通过保证约束集合的正不变性,可达到控制目标[7-8],同时避免计算系统的正可达集[9].Ames等[10]针对二次规划问题,定义了两类特殊的屏障控制函数:倒数屏障函数(reciprocal barrier function,RBF)与调零屏障控制函数(zeroing barrier function,ZBF),权衡了跟踪控制目标和系统安全约束之间的冲突.Panagou等[11]采用屏障控制函数实现了多智能体系统的定点静态编队和避障.Wang等利用屏障控制函数实现了有加速度约束的异构多智能体系统的无碰撞运动[12].文献[13]引入一类新的类李雅普诺夫屏障函数,基于势垒函数和最大逼近函数构建了一种多智能体系统的多目标控制框架.Han等[14]利用类李雅普诺夫屏障函数设计了基于梯度的分布式控制器,解决了通信受不确定参数干扰的多智能体鲁棒编队控制问题.文献[15]中,Han等学者进一步讨论了通信和测量受不确定参数干扰的多智能体的鲁棒多目标编队控制问题,用线性矩阵不等式判断具有不确定性影响的通信拓扑,并提出了一种新型的类李雅普诺夫参数化屏障函数.文献[16]中,对存在部分通信失效的非完整约束多智能体系统,将智能体进行分类并通过建立二维解析向量场,实现智能体的无碰撞和全局收敛协调控制.
本文提出了一种基于屏障控制函数的分布式算法,实现了在领航者-跟随者框架下非完整约束多智能体系统的动态编队和连通性保持控制.首先,对跟随者智能体定义了连通性屏障函数与相关约束集,并证明了连通性屏障函数是一种调零屏障函数,同时给出了调零屏障控制函数的相关性质;其次,对调零屏障控制函数构建了相应的子李雅普诺夫函数,通过分析证明了总李雅普诺夫函数在期望队形处一致取值为零,使编队轨迹全局渐进收敛;然后,对跟随者智能体设计了基于屏障控制函数的协同控制算法,其中线速度控制器保证跟随者速度的跟踪与队形的跟踪,而梯度型角速度控制器实现跟随者角度的矫正;最后,数值仿真结果验证了该算法的有效性.本文提出的协同控制算法的特点包括:1)该方法利用通信范围内的局部信息,在保证初始时刻与领航者的连通条件时,跟随者将始终与领航者保持连通,同时编队误差均能渐进收敛;2)本文设计的基于屏障函数的控制算法对文献[16]中的屏障控制函数算法仅能在领航者为静态时的编队情况进行改进,可实现领航者有常数线速度和角速度的编队情况;3) 该方法实现了队形控制主目标和连通性次级目标,通过增加新的约束屏障函数,可进一步增加次级控制目标数量,具有较强的灵活性与适用性.
2 问题描述
2.1 系统描述
非完整约束系统没有孤立的平衡点,因而没有局部渐近稳定平衡点,只存在包含原点的平衡流形.由于其运动过程中不可积分的非完整约束影响,导致系统的状态变量维数大于控制变量维数,使得非完整约束移动机器人系统的前行方向受到限制.本文研究的具有非完整约束的智能体i由如下运动学方程表示:

其中:pi ∈R3为智能体i的状态向量,由智能体质心的二维坐标ri=[xi yi]T和相对于给定坐标系x轴的方向角θi组成.ui=[vi wi]为控制输入,vi为线速度,wi为角速度.不失一般性,将智能体等效为空间圆柱形结构.
智能体上装备有距离测量传感器,在通信范围内可进行距离测量和信息交换.文中采用连通性半径Rc表示智能体连通范围半径,以便统一测量范围半径和通信范围半径,如图1 所示.需要指出的是,采用连通性半径的概念并不影响后续控制器设计的普适性.当测量范围和通信范围不一致时,可选取其中较小的一项作为连通性半径.
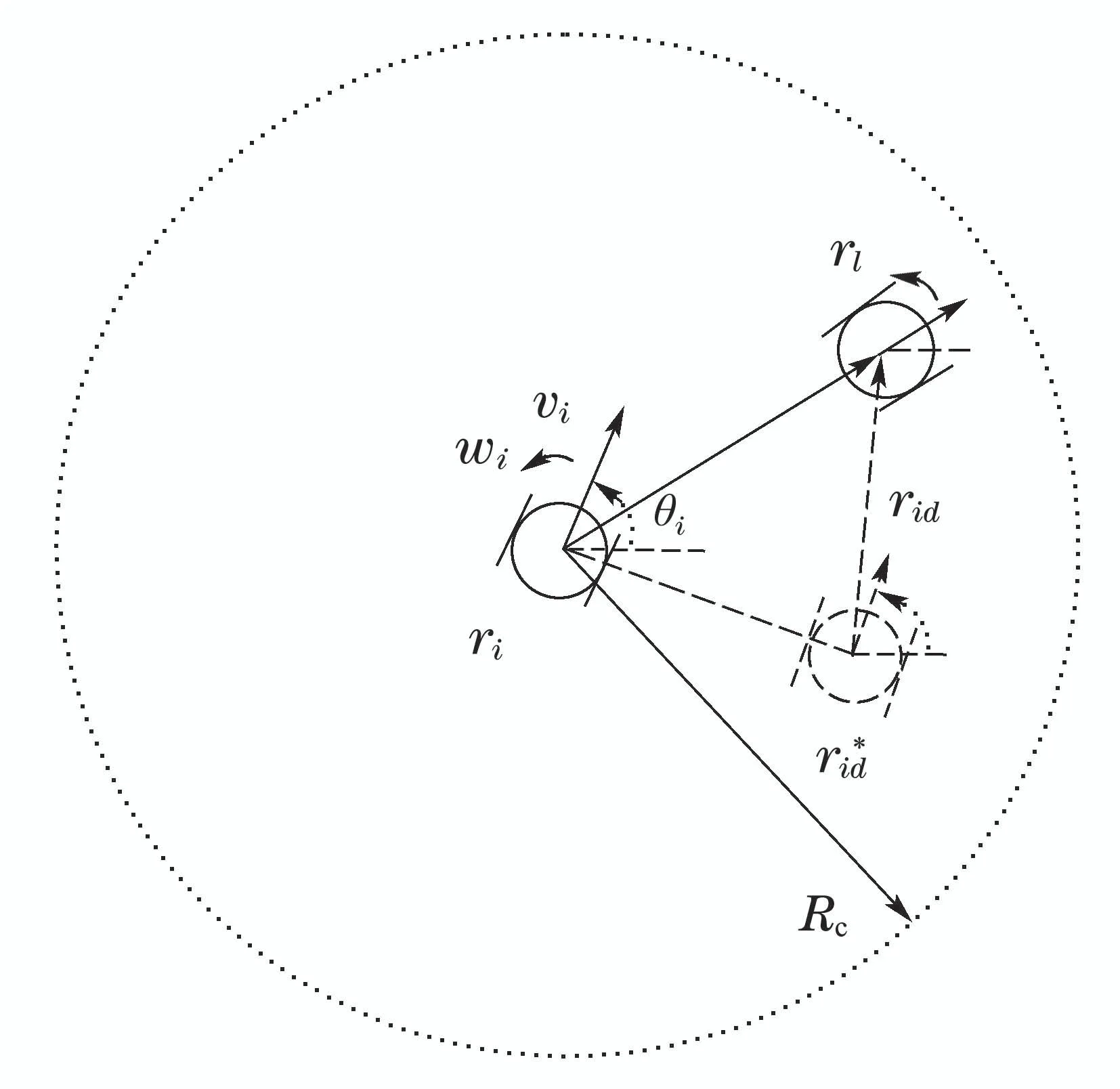
图1 非完整约束智能体与环境建模示意图Fig.1 Contraction of nonholonomic agent and environment
2.2 控制目标
本文的控制目标为:
1) 控制跟随者智能体i实现与领航者l之间的编队.期望队形为向量形式的固定距离rid ∈R2,定义为智能体i在队形内的相对其领航者l之间的期望位置,如图2所示.给定不同的期望动态目标点rid,则可以完成不同的上层主要任务,例如轨迹跟踪、围捕、护航等等.定义智能体i在x-y二维平面内的位置为实际期望位置,由如下表达式给出:

图2 连通性与圆形队形控制效果仿真结果Fig.2 Simulation results under circle formation

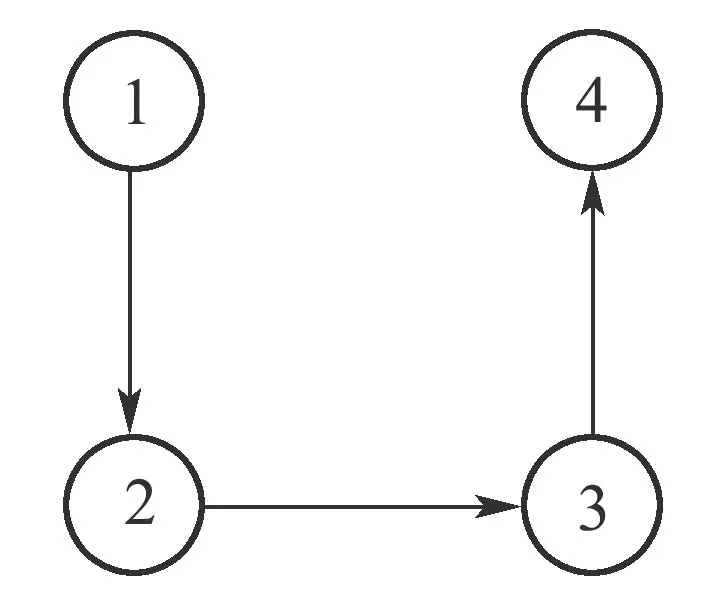
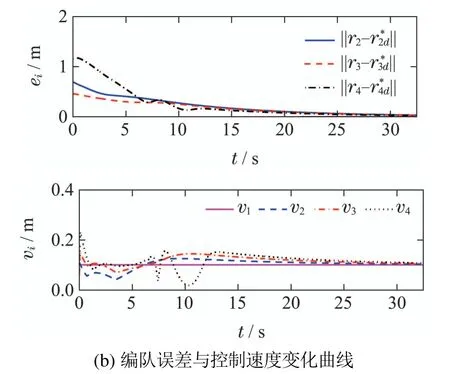
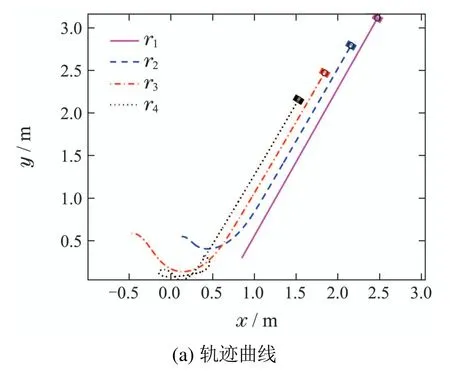
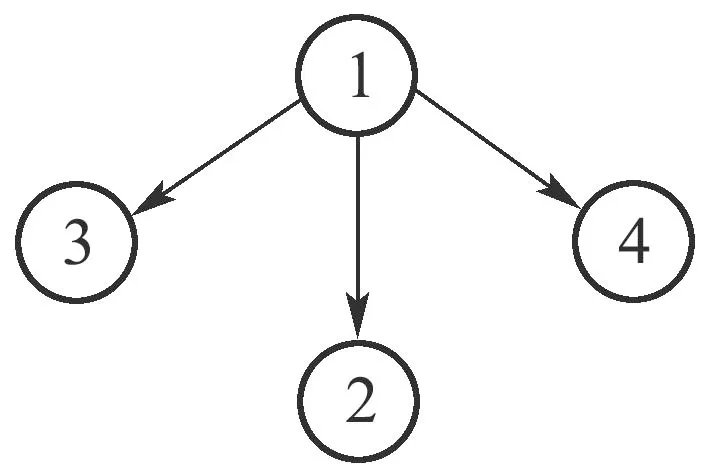
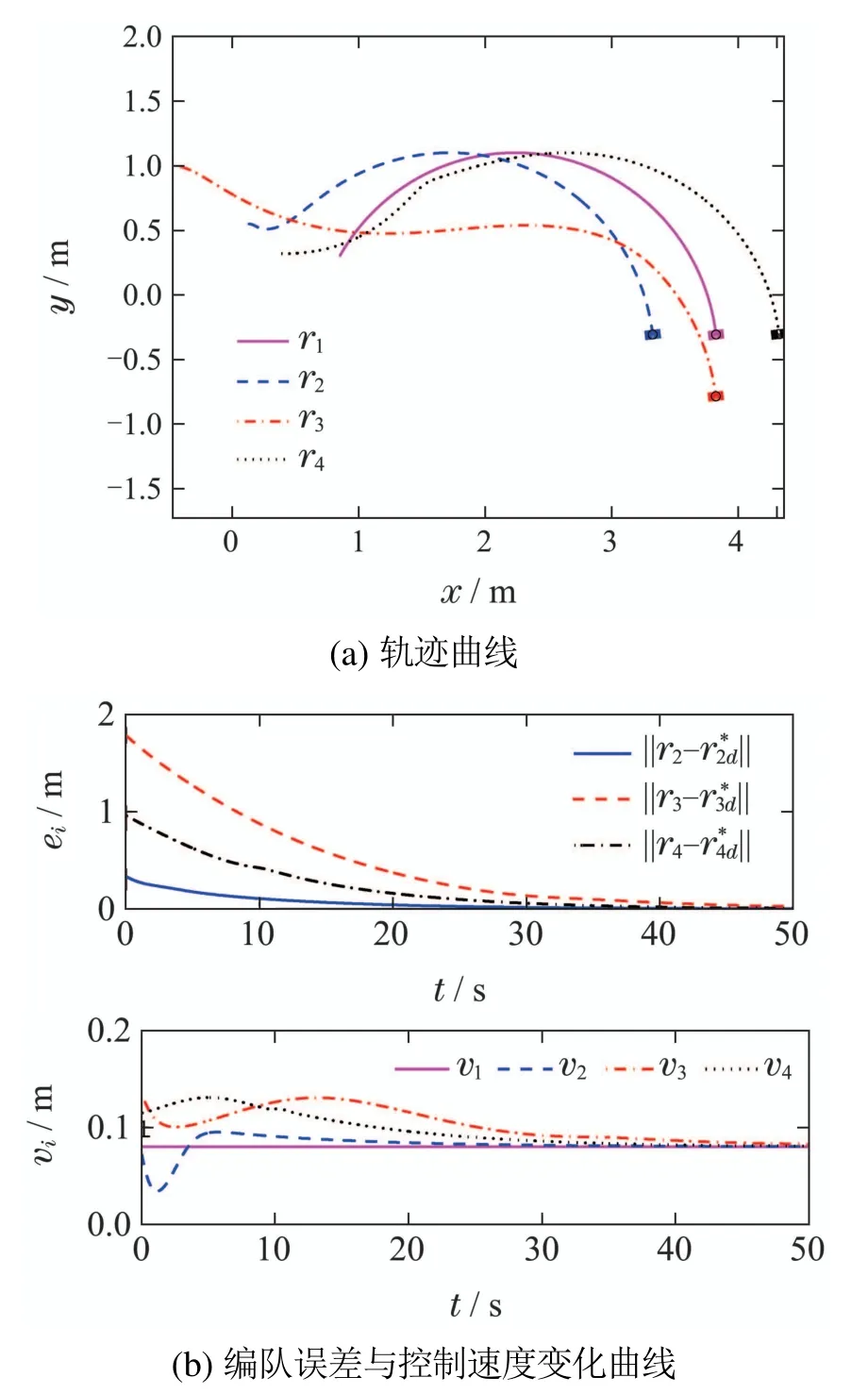
对于期望队形,应满足‖rid‖ 2) 保证领航者l始终位于智能体i的连通性区域内(以智能体i的质心为圆心,以Rc为半径的圆形区域).需要说明的是,对于轨迹跟踪、围捕、护航等上层任务,智能体形成特定队形的期望坐标点不再是固定点.考虑到每个智能体的实际期望位置是与领航者相关且时变的,因此可将每个智能体的期望坐标视作动态目标点,从而很容易扩展到轨迹跟踪问题. 为了保证智能体与其领航者之间能进行有效可靠的数据交换,与领航者之间的距离‖ri-rl‖小于等于连通性半径Rc.考虑到编队的动态性质,不同于文献[13]中的距离约束,本章中定义智能体i与领航者智能体l之间的连通性约束有如下形式: 上述约束不等式成立时,智能体i与领航者之间的连通性得以保证.定义每个智能体的连通性约束集为 接下来,设计合适的连通性屏障控制函数,如果能使其在期望位置点取值为零,在连通性约束集边界上趋于无穷,则该函数可作为约束条件(3)的惩罚函数.因此,给出如下对数形式连通性屏障控制函数: 对应屏障控制函数构建其子李雅普诺夫函数,且子李雅普诺夫函数需要在定义域内所有点处均取值非负,则定义 接下来,给出第2.2节中控制目标的总李雅普诺夫函数,使其在目标位置点一致取值为零,而在连通性约束边界处趋于无穷,有如下形式: 设计如下的分布式控制算法: 假设通过合理的设计控制器,可以对原系统进行时间尺度分离,将原系统分解为边界层系统(快变系统)和降阶系统(慢变系统).边界层系统描述方向角θi(t)的变化规律,降阶系统描述平面位置的ri(t)的变化轨迹.此时,相对于位置控制量xi(t)和yi(t),智能体的方向角θi(t)能更快速地控制到期望的角度.这类假设广泛应用于诸多文献中,例如文献[19-21].此时角度控制算法(23)可看作是比例微分控制器,且边界层系统θi(t)的平衡点为θi=φi.那么,在边界层系统的平衡点θi=φi处,李雅普诺夫函数沿降阶系统的导数如下式所示: 由定义可知,在约束集边界∂Cio内部,控制输入vi如式(22)中所设计;而在∂Cio外部,vi为零.此外,由式(23)中设计的角速度控制器可知,wi指向约束集Cio内部.因此,在约束集边界上∂Cio的点不会穿过边界,而始终保持在连通性边界上.相似地,对于无碰撞情况下多目标协同控制情况,广义Clarke梯度的导数由下式给出 由于在初始时刻t=0,由假设已知领航者在连通性约束集Cio内部,则‖ri(0)-rl(0)‖ 综上所述,除去初始时刻领航者l位于约束集边界∂Ci上,被控系统轨迹ri最终渐近收敛到动态目标点,并始终在连通性半径Rc范围内. 首先,由2个非完整约束智能体组成的领航-跟随者系统,初始状态为p1=[0.8 0]T,p2=[0 1.2 0]T,连通性半径Rc=1.5,领航者p1的初始速度为u1=[v1w1]T=[0.045 0.05]T,2号跟随者智能体相对于领航者的期望队形为rid=[0.4 0.4]T,i=2.协同控制算法(22)-(23)控制算法的参数为ki=0.01,λi=1(i=2). 由图2(a)中初始位置可知,领航者非常接近2号智能体的连通性区域的边界.图2(b)中分别展示了编队误差向量ei=ri-在x和y方向上分量的变化曲线、智能体之间相对距离dij的变化曲线,以及智能体的控制速度变化.由图2(a)可看出,2号智能体与其领航者之间的距离始终小于Rc. 其次,考虑由4个智能体组成的系统,其通信拓扑示意图如图3所示.跟随者智能体相对于各自领航者的期望队形均选取为rid=[0.3 0.3]T的排列队形.初始时刻p1=,p2=[0.13 0.55 0]T,p3=[-0.47 0.59 0]T,p4=[0.39 0.32 0]T.控制器参数ki=0.1,λi=1(i=2,···,4),领航者初始速度u1=[0.1 0]T.仿真结果图4(a)中给出采用本文控制算法(22)-(23)时,4个智能体平面轨迹变化曲线.图4(b)给出了本文控制法下跟随者智能体的编队误差向量ei=ri-,i=2,···,4的范数和控制速度vi的变化曲线. 图3 多智能体系统的通信拓扑示意图1Fig.3 Communication topology diagram 1 图4 排列队形编队仿真结果Fig.4 Simulation results under platoon formation 最后,不失一般性地考虑一对多(一个领航者对多个跟随者)时的编队与连通性保持情况,其拓扑结构如图5所示.初始时刻p1=[0.85 0.3]T,p2=[0.13 0.55 0]T,p3=[-0.47 1 0]T,p4=[0.39 0.32 0]T.跟随者智能体相对于领航者1 号的期望队形均选为r2d=[0.5 0]T,r3d=[0 0.5]T,r4d=[-0.5 0]T的三角队形.领航者的初始速度为u1=[0.1-0.05]T,控制器参数同上.最终仿真结果由图6给出. 图5 多智能体系统的通信拓扑示意图2Fig.5 Communication topology diagram 2 图6 三角队形编队仿真结果Fig.6 Simulation results under triangle formation 本文采用基于屏障控制函数理论,在领航-跟随者框架下对非完整约束多智能体系统设计了一种分布式协同控制算法.该方法中将队形控制、与领航者的连通性保持目标建模为系统的约束,再对该约束构建一个子李雅普诺夫函数,并与智能体角速度之间建立了联系.利用调零屏障函数不变集原理证明了该控制算法可实现上述两个协同控制目标.最终数值仿真验证了非完整约束智能体在不同队形下的连通性保持和编队效果,进一步证明了算法的正确性和有效性.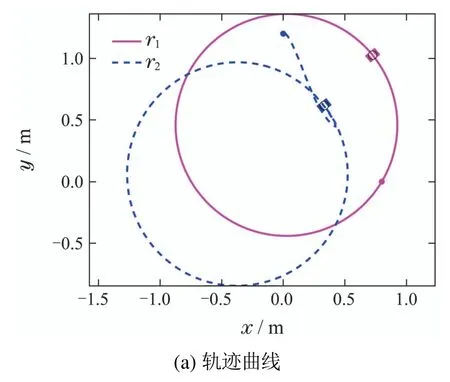
3 屏障控制函数
3.1 连通性屏障控制函数

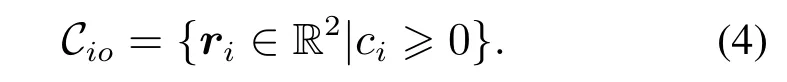


3.2 屏障控制函数的李雅普诺夫分析




4 基于屏障控制函数的分布式协同控制
4.1 基于屏障控制函数的分布式控制算法

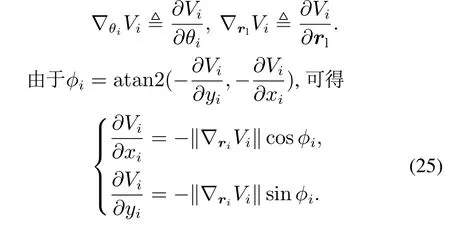




4.2 数值仿真
5 结语
