有限转角钢带的传动特性及预紧张力对输出特性的影响

鲁强,高志峰,钟小兵,戴军,黄秋,胡绍云

(西南技术物理研究所,四川 成都 610200)

0 引言

在伺服稳定平台或光瞄反射镜稳定系统中,为了实现稳定平台角度的准确传动和对目标的稳定跟踪,系统往往采用有限转角钢带传动的方式。即用紧固件将钢带固定于两个摩擦轮上,摩擦轮和钢带在一定角度范围内传动,实现稳定平台方位或俯仰角度姿态的改变。有限转角钢带传动系统具有转动范围有限、传递精度高、钢带厚度小、大变形且高度非线性等特点。

钢带传动在机械系统特别是精密机械传动中运用普遍,Zhu等讨论了传动带传动的疲劳寿命估算和失效分析,对能量或功率损失、皮带张力、皮带变形、皮带和皮带轮内部的应力和应变分布、接触摩擦力等进行了综述。Chen等建立了长距离钢带摩擦传动的动力学模型,仿真分析了预紧力与载荷、应力与应变的关系,得到了较好的传动精度。Zhu等提出在一定的运行条件下,由于共振条件或拍振现象,一定带跨内会产生较大的振动幅值。张杰等提出了一种采用钢带传动技术来提高稳定平台中轴系精度的设计方法。郑大宇等考虑带惯性力的影响,提高了带传动和分析模型的准确性。于方德等分析了钢带回弹的现象,发现带轮直径过小导致的钢带局部塑性变形是导致轴系回弹的根本原因。王旭东等研究发现传动带紧边和松边的拉力差是带传动产生弹性滑动的根本原因。王浩楠等通过推导不同传动位置钢带的应力计算公式,定性分析了不同位置钢带的应力大小。崔广军使用ANSYS和ADAMS软件联合对龙带进行了动力学仿真分析,得出了动态过程中龙带张力的应力变化图。张海峰等通过对输送钢带进行力学特性分析,得出了初始拉力、钢带厚度和滚筒直径是影响钢带应力变化的主要原因。潘炳财等针对反射镜稳定方式下的某型惯性稳定平台,用MATLAB/Simulink软件进行机电联合仿真,重点分析了钢带在不同刚度下对稳定精度的影响。徐珂对上反射镜稳定精度影响因素进行探讨,分析了2∶1传动机构对稳定的影响和作用。结合当前的工程实际应用可知,高端光电稳定及上反伺服机构的性能传动精度为0.006°左右,低速平稳性在0.006°/s到0.03°/s,稳定带宽为几十赫兹。因此,对于高精度反射镜稳像系统,钢带的传动特性对系统性能的影响显得非常灵敏和突出。

国内外学者研究的钢带传动系统多为长距离传输且负载较大,钢带做连续传动,而在精密稳定平台中有限转角钢带传动的研究则较少。现有文献在分析钢带传动打滑时,主要考虑钢带松边和紧边受到的力不同所导致的,没有从机理上建立蠕滑率和传动比数学模型。在分析预紧张力对钢带传动特性影响时,现有文献主要研究其对钢带应力、拉力的影响,很少建立钢带预紧张力的计算模型以及对输出特性的相关影响分析。由于有限转角钢带为高度弹性柔性体以及钢带预紧张力的影响,特别是系统受到电机驱动等内外动态扰动下,钢带在传动过程中会出现弹性滑动,导致传动比不精确、传动效率下降,严重影响钢带系统的输出特性。

本文为研究有限转角钢带传动产生弹性滑动的机理及相关传动特性,建立有限转角钢带系统弹性变形的运动学和动力学模型,用RecurDyn多体动力学仿真软件进行钢带系统刚柔耦合动力学仿真,建立有限转角钢带预紧张力的计算模型,并对预紧张力对钢带系统输出特性的影响进行仿真实验和物理样机实验。

1 钢带传动分析

钢带系统传动时的坐标系如图1所示。图1中,钢带传动的坐标系以摩擦轮的回转中心为原点,为主动摩擦轮坐标系,为从动摩擦轮处钢带上质点变化前的参考坐标系,为从动摩擦轮处钢带上质点变化后的参考坐标系,M点为钢带上质点变化前位置,N点为质点变化后位置,v为钢带传动速度,φ为钢带质点倾覆角,φ为翻滚角,ω为摇摆角。钢带系统在Oxy平面中传动,x和x、y和y、z和z坐标轴分别表示钢带与从动轮接触的某质点变化前后沿从动轮圆周运动切向方向、从动轮圆周运动径向方向以及从动轮回转轴方向。

1.1 有限转角钢带的传动状态分析

由于有限转角钢带为高度弹性柔体,在摩擦轮的不圆顺、定位轴承跳动、轴系装配间隙以及驱动电机动态扰动等因素特别是大量级振动冲击等外界扰动条件下,钢带在传动过程中会出现以下3种情况。

1)倾覆运动。钢带初始坐标系的Oz轴转动到Oz轴,转动角度为φ。倾覆角φ与两个摩擦轮上钢带的安装高度差、轴承轴向跳动等因素有关。

2)摇摆运动。钢带传动过程中,钢带初始坐标系的Ox轴转动到Ox轴,转动角度为ω。钢带摇摆角ω主要是由钢带弹性滑移和轴系间隙等因素造成的,摇摆运动若不加以控制,则会使钢带变形严重,甚至出现失稳现象。

3)翻滚运动。钢带传动过程中,钢带初始坐标系的坐标轴Oy轴转动到Oy轴,转动角度为φ。

4)横向运动。钢带沿摩擦轮半径方向Oy轴有一定的横移量δ。横向运动主要影响因素为定位轴系的安装间隙以及钢带的弹性变形。

图1所示为钢带传动过程中钢带上某质点的运动状态变化图。由于有限转角钢带为高度柔性体传动,除钢带与摩擦轮接触斑上相接触的质点对之间存在相对刚性运动外,钢带上与摩擦轮接触的质点位置也会发生明显改变。这种接触质点的相对刚性运动和位置改变严重影响钢带系统的传动精度和平稳性,是引起钢带磨耗、接触疲劳和破坏的重要原因。

质点在变化前后的参考坐标系中有如下转换关系:

式中:B为转换矩阵,根据坐标系的旋转特点可以求出转换矩阵如下:

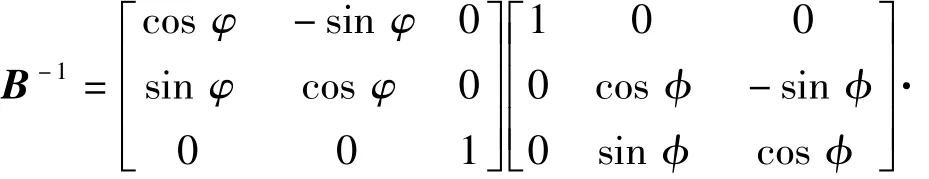
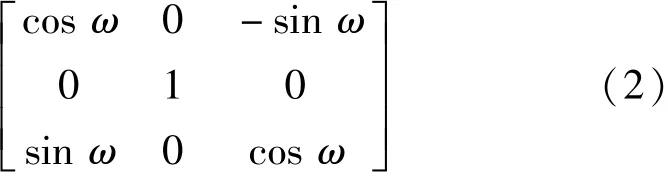
进一步计算,得

根据(1)式可以求出钢带上接触点在相对于变化前坐标系Oxyz中的位置,将变化前的坐标系定义为原始坐标系,原始坐标系中钢带上接触质点的坐标为(0,R,0),R为摩擦轮半径,当钢带出现以上4种变化时,钢带上质点在原始坐标系中的坐标向量为

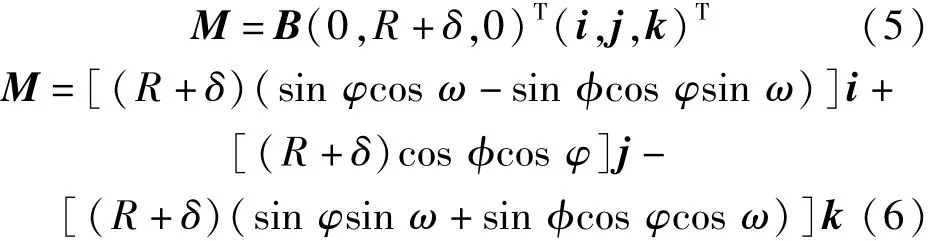
式中:δ为钢带横移量;i、j、k分别表示原始坐标系中x轴、y轴、z轴方向的单位向量。

为了求得钢带上质点的绝对速度,将钢带上与摩擦轮接触点始终保持重合的空间点视为牵连点,该点的速度即为钢带上接触点处的牵连速度。牵连速度等于质点在空间位置变化量对时间的导数,设牵连速度为v,则有

将钢带接触点相对速度表示在原始坐标系:

式中:γ为主动轮的转速。由速度的合成定理,可以求得钢带上接触点的绝对速度为

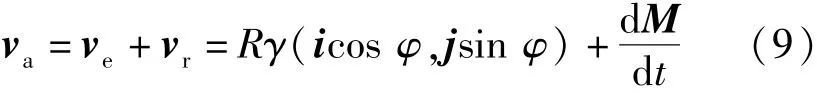
(7)式和(8)式代入(9)式,得到钢带上接触点沿x轴、y轴、z轴方向的速度分量分别为

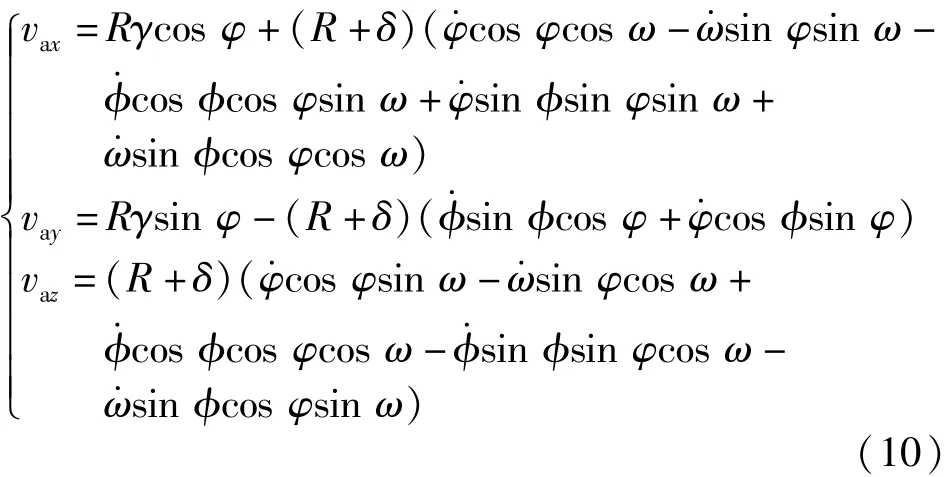
1.2 有限转角钢带的传动比分析与计算

在钢带运动状态分析的基础上,需要进一步求得有限转角钢带传动的蠕滑率和传动比,以获得蠕滑率和传动比与钢带相关参数之间的关系。

蠕滑率计算公式:

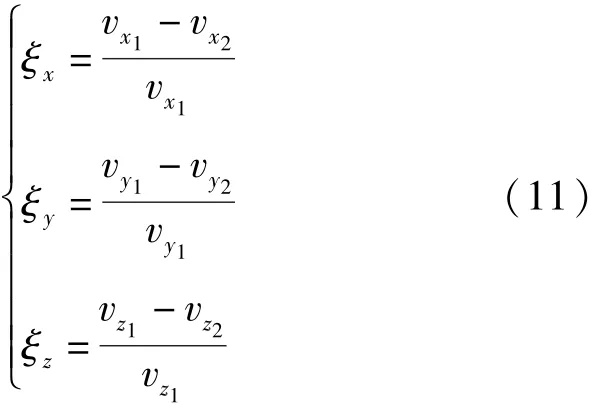
式中:ξ、ξ、ξ分别为钢带沿轴、轴、轴方向的蠕滑率分量;v和v为钢带在摩擦轮接触点水平切线方向和垂向的初始速度;v、v为钢带滑动后沿摩擦轮切线和垂向方向的速度;v、v分别为钢带在摩擦轮接触点滑动前和滑动后沿摩擦轮轴向的速度。

钢带与摩擦轮接触传动时,取宽度为的单位长度钢带,其形状为矩形,如图2所示。图2中,、为钢带紧边和松边的张力,为摩擦轮回转中心,从中心分别连接、、、4个点,矩形为钢带某一单位截面积,线段与分别与线段相交于点和点,为钢带外缘传动角度,为钢带内缘传动角度,Δ为内外缘传动角度差。由于钢带有一定厚度,在相同时间内钢带内缘和外缘在摩擦轮上滚过的角度不等,带与轮之间会出现自身打滑现象。

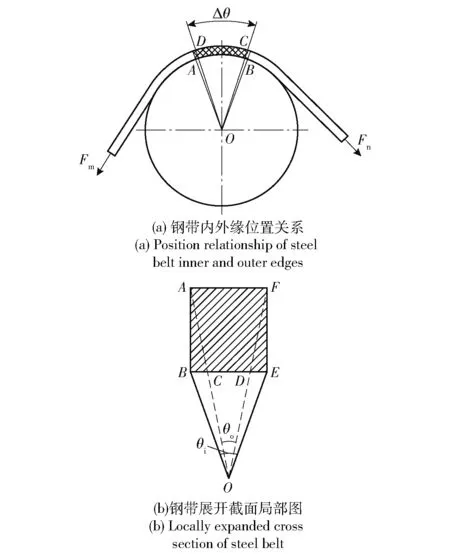
图2 钢带与摩擦轮的接触关系图Fig.2 Contact relation between steel belt and friction wheel

令==,==,摩擦轮半径=,钢带外边缘到的距离==+,钢带内边缘到的距离==,则外边缘和内边缘之间的轨迹差值和即为产生滑动的原因。

首先根据如下公式计算+的长度:

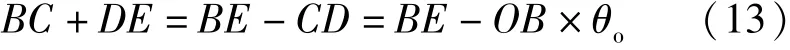
(12)式代入(13)式,有

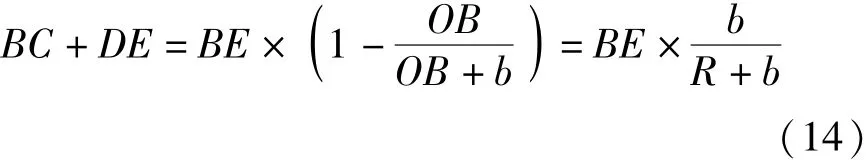
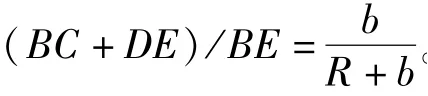
在从动摩擦轮上,钢带从松边到紧边的拉力逐渐增大,带速大于摩擦轮的线速度。钢带在传动过程中,由于内外缘的运动弧长不同,会使钢带产生一定的滑动。由(11)式和(14)式,钢带内外缘产生的纵向蠕滑率为

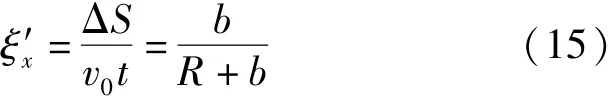
式中:Δ为单位长度上的滑移位移;为钢带初始速度;为单位时间。由此可得钢带传动过程中的蠕滑率为

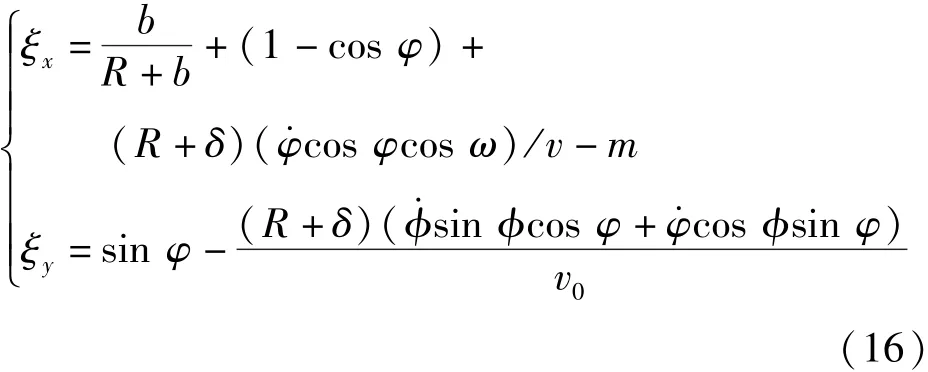
从(16)式中可以看出,钢带的蠕滑率主要是横向蠕滑率ξ,省略其高阶小量,则有

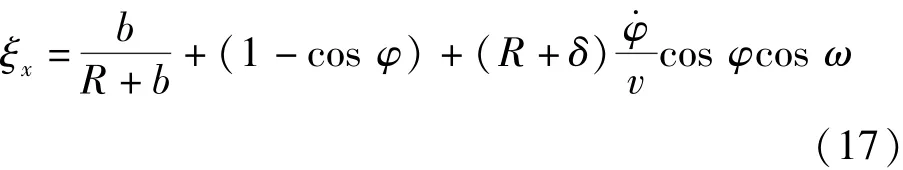
进而可得传动比与蠕滑率ξ的关系为

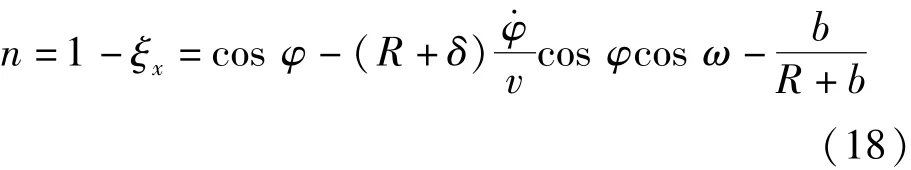
由此可见,钢带系统的传动比主要影响因素包括摩擦轮半径、钢带厚度、钢带翻滚角度、翻滚角速度与钢带传动速度比以及钢带横向位移等。

以上研究结果表明:摩擦轮半径越小、钢带厚度越大、翻滚角速度与钢带传动速度比越大,则钢带打滑就越严重,对钢带传动比影响越明显。钢带翻滚角速度与钢带传动速度比的影响因素主要包括钢带的刚性、钢带长度、驱动电机动态扰动以及振动冲击外界力学条件等。

2 钢带系统刚柔耦合动力学分析

纯刚性体与刚性体仿真研究时,输出结果过于理想,不能反映真实的工况;刚性体和柔性体的耦合既可以得到与实际工况相符合的精度要求,又具有较高的仿真计算效率,采用多柔性体动力学软件RecurDyn对伺服平台钢带系统进行刚柔耦合动力学分析。

2.1 Recur Dyn多柔体动力学建模

RecurDyn多柔性体动力学结合了对刚体运动仿真的多体动力学和对柔性体应力和变形仿真的有限元法,以有限元方法描述多体系统中一个或多个柔性体机构的行为,能够很好地考虑和保障系统在运行过程中的几何变形、弹塑性变形、颤动等特征。另外,对于非线性接触问题,RecurDyn软件提供的算法考虑并保障了柔性体与刚体、柔性体与柔性体的挤压、摩擦以及碰撞等特征。

RecurDyn多柔性体动力学仿真可以较好地反映钢带传动过程中的大变形、大幅颤动等特征,从而更加准确地反映钢带传动过程中传动比和传动精度的变化情况。

2.2 有限转角钢带系统刚柔耦合模型

伺服平台中,钢带传动系统作为稳定平台角度和速度的传递环节,直接关系到位置姿态和跟踪状态的准确性。钢带与摩擦轮在传动过程中,接触类型为大柔性体接触;将钢带看作柔性体,摩擦轮视为刚性体,能够尽可能地保证带与轮接触类型的真实性,同时简化计算模型,便于仿真计算。

图3所示为钢带与摩擦轮的刚柔耦合模型。首先用UG软件建立钢带系统模型,在ANSYS APDL软件中建立钢带刚性区域和约束点,并生成柔性体文件。然后将钢带传动模型导入RecurDyn动力学软件中,将钢带替换成上述生成的柔性体文件,通过柔性体中的约束点分别将钢带与两摩擦轮固定连接,使仿真模型与真实样机的连接情况一样,保证传动形式一样。最后完成钢带传动系统刚柔耦合模型的建立。

图3 钢带传动刚柔耦合模型Fig.3 Rigid-flexible coupling model of steel belt system

2.3 刚柔耦合的接触模型

接触力的计算方法有两种,一种是基于回归的接触算法,通过惩罚参数和回归系数来计算接触力。其中惩罚参数施加了单位约束,回归系数决定接触时的能量损失。另一种是基于碰撞函数的接触算法,刚柔接触采用基于碰撞函数的接触算法时,运用函数库中IMPACK函数来计算接触力。根据IMPACK函数来计算两构件之间的接触力时,接触力由两部分组成:一是两构件之间相互切入产生的弹性力;一是由于相对速度产生的阻尼力。接触碰撞模型如图4所示。图4中,为法向接触刚度系数,为阻尼系数。

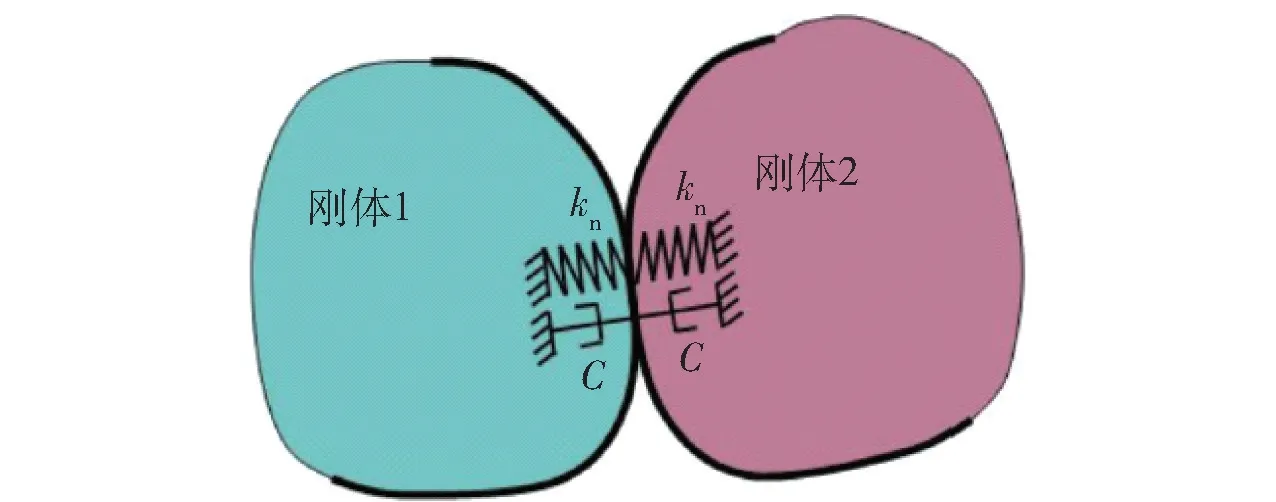
图4 接触碰撞模型示意图Fig.4 Sketch of contact collision model

RecurDyn软件计算接触力是基于Hertz接触理论,并在此基础上做了改进,计算接触产生的法向接触力的公式为

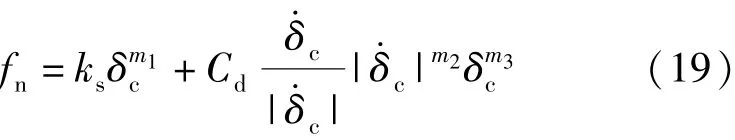
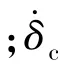
2.4 钢带预紧力计算模型

钢带传动时钢带保持一定的预紧力,是保证钢带有效传动的必须条件,预紧力过小,摩擦力不足,容易发生打滑;预紧力过大,会降低钢带的寿命,同时加大回转轴系轴承的磨损。因此,合适的钢带预紧力十分重要,但钢带预紧力往往不易直接准确测量,特别是在受限空间内,有限转角钢带系统中钢带预紧张力更不易测量。

为了求得钢带的预紧张力,需要先计算出钢带与摩擦轮装配后钢带的伸长量。再通过拉伸实验得到钢带张力和伸长量的关系曲线,根据曲线关系,可以得到对应钢带伸长量的钢带预紧力大小。

下面推导垫片宽度、厚度与钢带张力之间的关系。

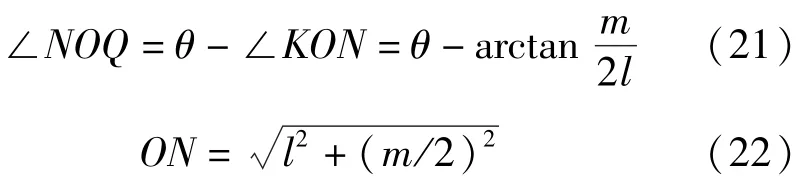
由余弦定理,有

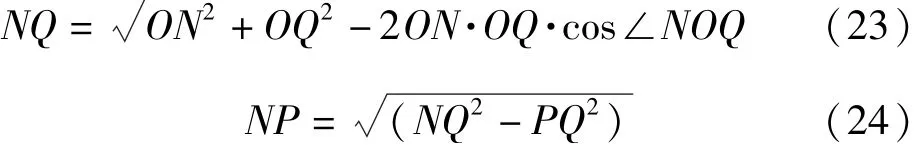
由弧长计算公式,有

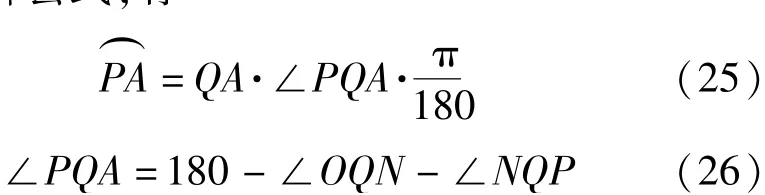
由余弦定理,有

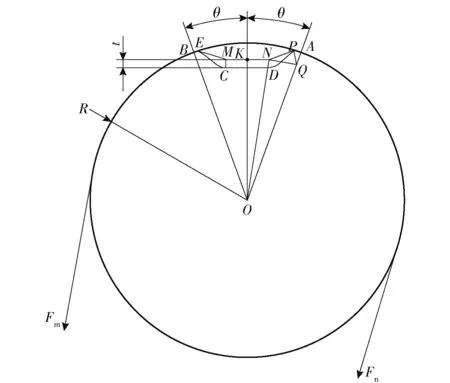
图5 钢带伸长量计算几何模型Fig.5 Geometric model for length variation of steel belt

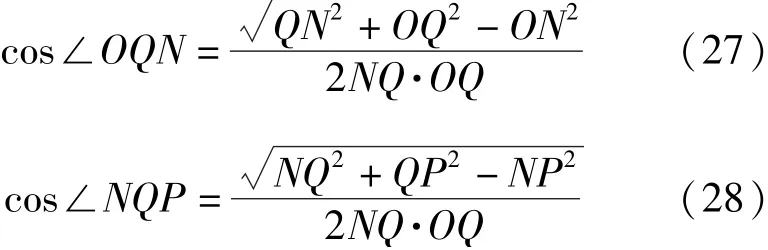
(24)式～(30)式代入(20)式,可计算钢带的伸长量。

设为钢带弹性模量,为钢带横截面积,根据应力的计算公式:

可求得钢带张力=。结合一般的胡克定律=,则有

2.5 钢带张力与伸长量的关系分析

对于钢带,其张力与伸长量之间的关系并不是一般情况下的胡克定律,而是符合修正后的胡克定律,需要对钢带进行拉伸实验以得到其张力与伸长量的关系。

在钢带拉伸实验中,钢带材料选用06Cr19Ni10,钢带厚度0.08 mm,宽度4.5 mm,长度180 mm,钢带拉伸实验装置如图6所示。

图6 钢带拉伸实验设备和装配关系Fig.6 Tensile test of steel belt

钢带在拉力测试机上的装配关系为:先用拉力机的上下夹紧器分别把钢带两端夹紧,再把两个引伸计分别与钢带中间的两位置接触,接着钢带在拉力机的作用下不断拉伸,直到被拉断,得到钢带张力与伸长量之间的关系曲线,如图7所示。

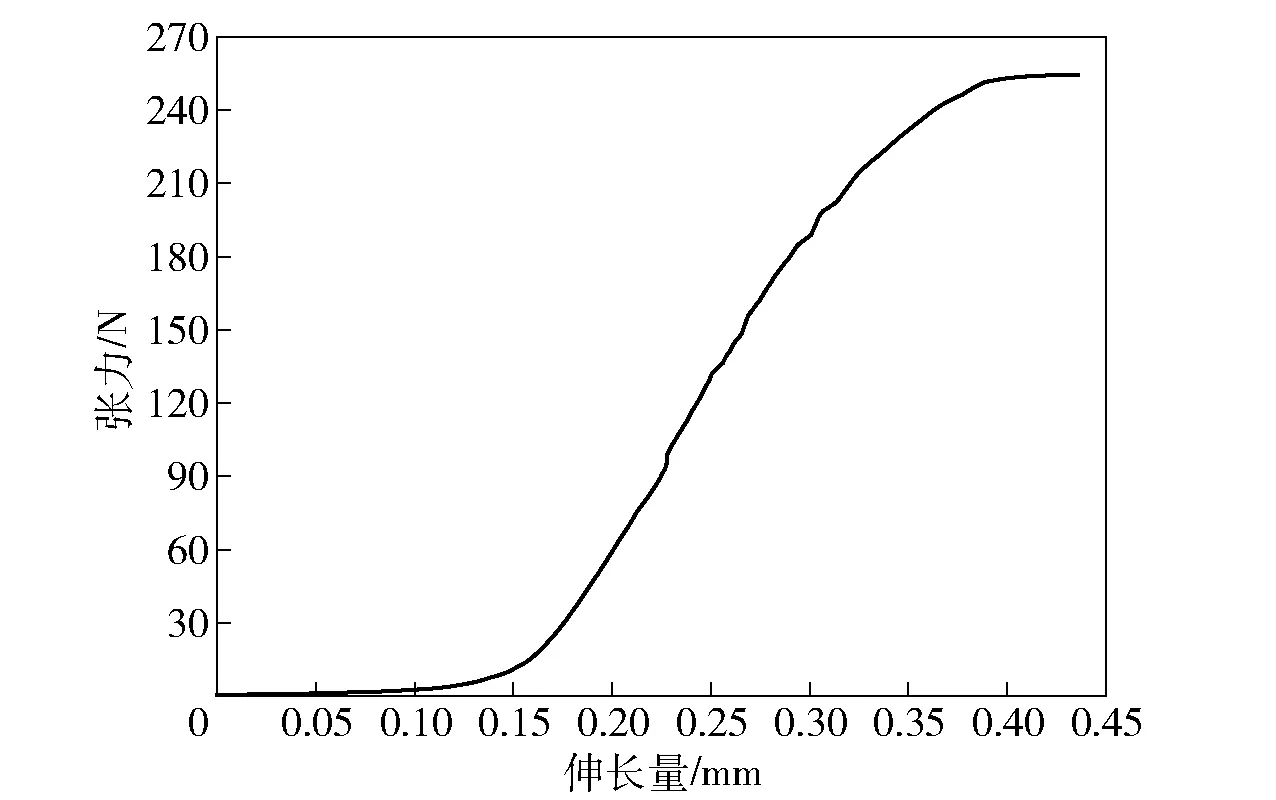
图7 钢带张力与伸长量的关系图Fig.7 Relation between tension and elongation of steel belt

根据图7,将钢带的拉伸过程分为3个阶段,分别是:拉伸量为0～0.10 mm的弹性阶段1,拉伸量为0.10～0.15 mm的阶段2,以及拉伸量为0.15～0.40 mm的阶段3。这3个阶段的张力与伸长量关系,可以通过线性拟合满足下面公式:

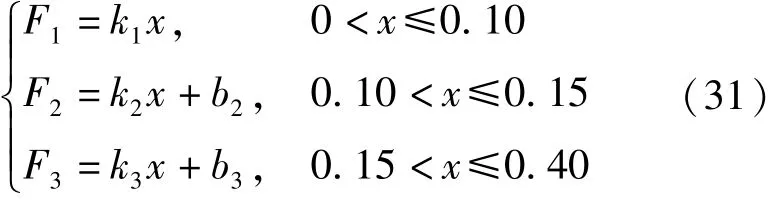
式中:、、分别表示对应阶段的张力;、、分别表示钢带弹性阶段1、阶段2和阶段3的刚度系数;、分别表示阶段2和阶段3的截距系数;为钢带伸长量。

采用最小二乘法进行线性拟合,得到如下一元线性回归方程:

联立(20)式和(32)式,可以计算出钢带的预紧力大小。

由于实际操作中是通过调节调整垫片的厚度,间接达到调节钢带预紧力的目的,工程应用中可根据从动轮的力矩关系计算出所需的预紧力大小:

式中:为等效张力;为轴系摩擦阻力力矩;为负载转动惯量;为角加速度。设为预紧张力,由(33)式并结合紧边和松边的受力关系

以及柔性体摩擦的欧拉公式

可以计算出平台需要的钢带预紧张力,然后根据(32)式逆向计算出钢带的伸长量,即可计算出调整垫片所需的厚度。

钢带调整垫片的厚度直接影响到钢带预紧张力的大小,钢带预紧力过小,将导致钢带轮与钢带之间出现严重的蠕滑现象,影响传动效率,因此在实际钢带传动中,需要选择合适厚度的调整垫片,以获取较好的预紧力。

3 预紧张力对钢带系统传动特性的影响

钢带预紧张力的大小直接关系到钢带系统的输出精度和传动平稳性,需要对钢带预紧力与系统输出特性的关系进行研究。钢带传动系统中的参数如表1所示。

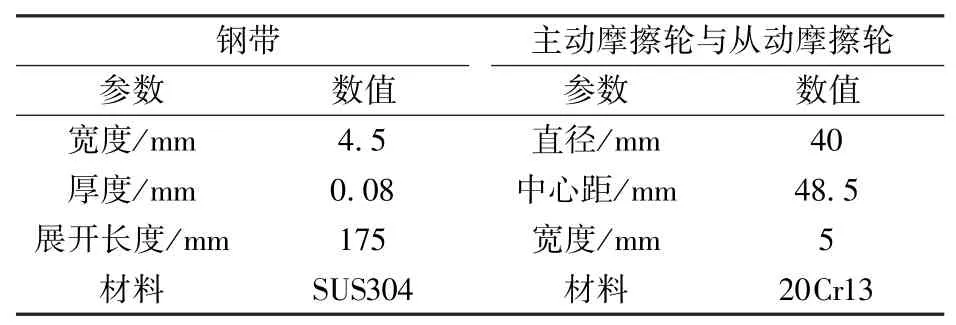
表1 钢带传动系统相关参数Tab.1 Parameters of steel belt transmission system

3.1 多体动力学仿真实验

在钢带传动系统刚柔耦合模型基础上,给摩擦轮赋予摩擦力和转动惯量,并合理设置钢带刚度和刚柔接触。本文伺服平台系统中钢带传动的负载=1.6 kg,转动惯量J=4×10kg·m,考虑轴系摩擦阻尼和线扭矩影响,摩擦轮转动时动摩擦因素=0.1。实验中选取钢带拉伸量的调整垫片厚度分别为0 mm、0.4 mm、0.8 mm,根据(22)式可计算出钢带的拉伸量分别为0.40 mm、0.22 mm、0.15 mm。

根据钢带张力与伸长量的关系,可以求出垫片厚度分别为0.8 mm、0.4 mm、0 mm,以及对应钢带拉伸量分别为0.15 mm、0.22 mm和0.40 mm时的预紧张力大小,如表2所示。

表2 不同垫片厚度及对应钢带拉伸量下钢带的预紧张力Tab.2 Pre-tension force of steel belt for different thickness of gasket

预紧张力对钢带系统输出转角和角速度的影响如图8和图9所示。

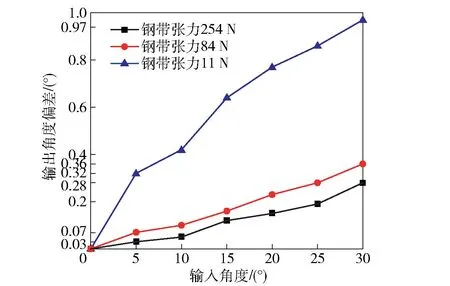
图8 预紧张力对钢带系统输出角度影响(仿真结果)Fig.8 Effect of pre-tension force on output angle of steel belt transmission system(simulation results)

从图8中可知:在相同输入角度下,预紧张力越大,钢带系统的输出转角偏差越小;在同一钢带预紧张力下,随着输入转角的增加,钢带系统输出转角的偏差增大;当输入转角为5°时,输出转角偏差分别为0.32°、0.07°、0.03°;当输入转角为30°时,输出转角偏差分别增大为0.97°、0.36°、0.28°。

从图9中可知:随着钢带预紧张力增大,钢带系统输出角速度的超调量先变小后变大;预紧张力越大,输出角速度的波动性和误差较小;当预紧张力为11 N时,传动系统的角速度超调量达到40%以上,且在1 s后趋于稳定,波动时间较长;当预紧力增加到84 N时,系统输出的角速度超调量为1%,系统0.2 s后稳定,系统平稳性好;当预紧力增加到254 N时,系统输出的角速度超调量为7%,系统0.3 s后稳定,系统平稳性相对变差。

图9 预紧张力对钢带系统输出角速度影响(仿真结果)Fig.9 Effect of pre-tension force on output angular velocity of steel belt transmission system(simulation results)

3.2 物理样机实验

钢带传动系统物理样机如图10所示,其工作原理为:电机回转轴与主动摩擦轮连接,钢带分别与主动摩擦轮和从动摩擦轮通过螺钉连接固定,且钢带与从动摩擦轮连接处有张力调整垫片。钢带传动系统安装在平台外框上,电机驱动主动摩擦轮转动,通过钢带将传动传递给从动摩擦轮,从而带动整个回转平台转动。陀螺速率测量装置安装在回转负载平台上,编码器或电位器测角装置安装在从动摩擦轮回转轴上。

图10 稳定平台中钢带传动系统Fig.10 Steel belt transmission system on stabilized platform

图11所示为稳定平台控制系统和输出采集系统,钢带传动速度通过挠性陀螺测量,角度通过电位器测量。通过操纵计算机输出相关指令,控制传动系统。

针对钢带预紧张力对钢带系统的影响,物理样机实验中负载、钢带预紧张力等参数与仿真实验相同。预紧张力对钢带系统输出转角和转速影响的实物实验结果如图12和图13所示。

从图12中可知,相同输入转角下,钢带张力增加,钢带系统输出角度偏差较小。由于钢带系统刚柔耦合动力学仿真时,将钢带进行有限元柔性体处理,且充分考虑钢带张力、负载惯量以及摩擦力等因素,实物实验中张力对钢带系统输出特性的影响与仿真实验大致相同。

从图13中可知:相同输入角速度下,钢带张力越大,系统输出的角速度偏差越小,可见增大钢带张力可以提高钢带系统输出转速的稳定性;相同张力条件下,输入角速度越大,钢带系统的输出角速度偏差越大;实物实验与仿真实验结果相吻合。

此外,影响钢带传动的因素还包括钢带中心跨距、负载转动惯量、轴系摩擦及装配精度、钢带厚度等因素。钢带的中心跨距越大,钢带传动过程中易发生弯曲变形,钢带传动的平稳性越差;负载惯量越大、轴系摩擦越大,系统响应变慢且平稳性越差;为了获得更高的传动精度,主动轮轴系和从动轮轴系的平行度以及稳定反射镜回转轴系的同轴度都需要更高要求;钢带厚度越厚,系统输出误差越大。因此,在实际选型和设计中,要充分考虑钢带系统的相关参数和布局,以获得更好的输出特性。

4 结论

本文对稳定平台中有限转角钢带系统的传动特性进行了分析,重点分析了有限转角钢带传动系统的蠕滑率和传动比数学模型;建立了钢带预紧张力的数学模型和刚柔耦合的动力学模型,在此基础上研究了钢带预紧张力对钢带系统输出特性的影响,相关结果能很好地反映有限转角钢带系统的传动特性。实际工程应用中,由于加工误差、装配误差以及线的扭矩等综合因素影响,物理样机的实验结果与仿真结果的差别会偏大。得出主要结论如下:

1)钢带厚度、翻滚角、翻滚角速度与钢带传动速度比、横向位移以及摩擦轮半径是钢带蠕滑率和传动比的主要影响因素。有限转角钢带蠕滑率与钢带厚度、翻滚角、翻滚角速度与钢带传动速度比、横向位移为正相关关系,与摩擦轮半径为负相关关系。工程中要根据实际情况,选择合适的钢带参数。

2)随着钢带预紧张力的增大,钢带传动系统输出转速的超调量减小,系统输出精度越高且传动越平稳;但预紧力过大,输出转速的超调量也会变大;因此实际应用中应该选取合适的预紧力,过大或者过小的预紧力都会使得输出转速的超调量变大,且预紧力过大易造成钢带疲劳损坏。本文系统中,当预紧力为11 N时,系统超调量为40%,输出角度误差为6.4%;当预紧力增加到84 N时,超调量减小到1%,输出响应时间减小为原来的20%,且输出角度误差减小到1.4%。

3)钢带蠕滑率、传动比和预紧张力的数学模型,可为相关研究提供理论基础和有效参考。