复合地基黏性土路堤土拱效应分析

刘吉福，余 烈

（1. 广东省交通规划设计研究院股份有限公司，广东 广州 510507；2. 东莞理工学院 生态环境与建筑工程学院，广东 东莞 523015）

0 引 言

我国沿海地区河网密布，一方面高速公路被交道路和河道多，导致路堤普遍较高；另一方面，对高速公路的建设工期、质量要求不断提高。上述两方面的因素导致越来越多的高速公路软基路堤采用复合地基。随着砂石料价格不断上涨，除复合地基褥垫层可能采用砂石料等无黏性土外，路堤其余部分基本上均填筑黏性土，部分路基甚至取消了无黏性土褥垫层。路堤下复合地基桩间土沉降大于桩顶沉降，导致桩（帽）顶面以上的路堤中形成土拱。土拱效应分析对复合地基沉降计算、稳定分析等均非常重要[1-4]。目前对土拱效应的研究常用方法有模型试验、现场测试、数值分析、理论分析[5-13]等。BS 8006—2010采用计算涵洞应力的MARSTON公式和HEWLETT公式[14]。我国公路规范采用陈云敏公式[15]。MARSTON公式计算的桩土应力比、桩（帽）承担荷载与单桩负责面积内桩（帽）顶面以上路堤荷载的比例（简称桩荷载率）与填料性质无关，路堤高度较大时桩土应力比、桩荷载率偏小[14]。HEWLETT等[5]、陈云敏等[6]、强小俊等[7]对土拱效应进行理论分析时均假设土拱为球形。HEWLETT等[5]、陈云敏等[6]假设拱顶、拱脚均为无黏性土。HEWLETT等[5]分别计算拱顶、拱脚屈服对应的桩帽荷载率并取其中的小者。陈云敏等[6]认为路堤较低时拱脚、拱顶都未进入极限状态，按极限状态得出的桩顶荷载与桩间土荷载之和大于路堤重力；当路堤较高时由极限状态算出的桩顶荷载与桩间土荷载之和小于路堤重力；只有当路堤高度为某一特定值时才能满足荷载平衡条件。因此假设拱顶、拱脚屈服程度相同，对被动土压力系数乘以不大于1的屈服系数，通过试算计算桩帽荷载率和桩土应力比。强小俊等[7]采用文献[6]的思路推导了黏性土路堤的土拱效应公式，需要试算计算桩土应力比，且路堤高度较小时计算的桩间荷载集度、桩土应力比为负值，明显不合理。

工程实践中，刚性桩复合地基通常采用桩帽复合地基，也有专家认为桩梁复合地基更有利，导致设计人员非常纠结。

为使土拱效应分析更加符合工程实际情况，推导了可以考虑填料黏聚力的土拱效应公式。针对桩帽复合地基与桩梁复合地基优劣的争议，推导了桩顶设置连梁时的土拱效应公式，并通过计算分析了桩梁复合地基和桩帽复合地基的优劣。

1 桩帽复合地基

根据 HEWLETT等[5]的假设，对于正方形布置的刚性桩，4根桩之间的土拱可近似地拆分为两部分，一部分是两端直接作用于桩帽顶部的4个三棱形平面土拱，另一部分是作用于4个三棱平面土拱上的球形土拱。

1.1 拱顶屈服控制的桩土荷载

取球形土拱拱顶土单元进行受力分析，根据图1中土单元径向受力平衡条件可得：

图1 拱顶土单元受力Fig. 1 Stress of soil element of vault

当球形土拱拱顶屈服时，其径向和切向应力之间的关系为：

式中：c1为拱顶土的黏聚力；Kp1为拱顶土的被动土压力系数。

1.2 拱脚屈服控制的桩土荷载

取三棱形平面土拱拱脚土单元进行受力分析，根据图2中土单元径向受力平衡条件可得：

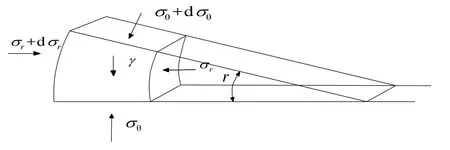
图2 拱脚土单元受力Fig. 2 Stress of soil element of arch foot

当三棱形平面土拱拱脚土单元屈服时，径向应力和切向应力之间的关系为：

1.3 基于土拱应力分析确定的桩土荷载

当拱顶屈服对应的桩帽间荷载集度大于拱脚屈服对应的桩帽间荷载集度时，如果采用拱脚屈服对应的桩帽间荷载集度，则会导致式（2）不成立。因此，此时拱脚不屈服，应采用拱顶屈服对应的桩帽间荷载集度，即采用式（8）计算桩帽间荷载集度。

当拱顶屈服对应的桩帽间荷载集度小于拱脚屈服对应的桩帽间荷载集度时，如果采用拱顶屈服对应的桩帽间荷载集度，则会导致式（12）不成立。因此，此时拱顶不屈服，应采用拱脚屈服对应的桩帽间荷载集度，即采用式（19）计算桩帽间荷载集度。

因此，桩土荷载、桩土应力比应根据土拱实际屈服位置的受力分析确定，即桩帽间荷载集度应取拱顶屈服、拱脚屈服对应的桩帽间荷载集度中的大者，桩帽荷载应取拱顶屈服、拱脚屈服对应的桩帽荷载中的小者，桩土应力比应取拱顶屈服、拱脚屈服对应的桩土应力比中的小者。

2 桩梁复合地基

桩顶框架梁的作用与桩帽的作用相同，其中横向连梁同时可以减少刚性桩的水平位移，因此只分析桩顶设置横向连梁的情况，设连梁宽度为，此时仅有垂直连梁的平面土拱。

2.1 拱顶屈服控制的桩土荷载

取平面土拱拱顶土单元进行受力分析，根据土单元径向受力平衡条件可得：

2.2 拱脚屈服控制的桩土荷载

进而由式（29）求得桩土应力比。

2.3 基于土拱应力分析确定的桩土荷载

与1.3节同样道理，连梁间荷载集度取拱顶屈服、拱脚屈服对应的连梁间荷载集度中的大者，连梁荷载取拱顶屈服、拱脚屈服对应的连梁荷载中的小者，桩土应力比取拱顶屈服、拱脚屈服对应的桩土应力比中的小者。

3 工程验证与方法对比

3.1 工程验证

（1）案例1

文献[8]中广东佛山一环城市快速路乐从试验段F区右幅管桩正方形布置，间距2.4 m，桩长12 m，以穿透第一层软土进入硬土层2 m。桩帽边长1 m。桩帽顶面铺设一层钢塑土工格栅，格栅以上填筑细砂，细砂厚度为 3.2 m，格栅以上桩土应力比实测值为 9.35。由于细砂经过碾压，内摩擦角取 30°，黏聚力取0 kPa，重度取18 kN/m3。按照各种方法得到的桩土应力比见表 1。由于管桩未穿透第二层软土，MARSTON方法按照摩擦桩计算。可见，本文方法计算的桩土应力比更接近实测值。

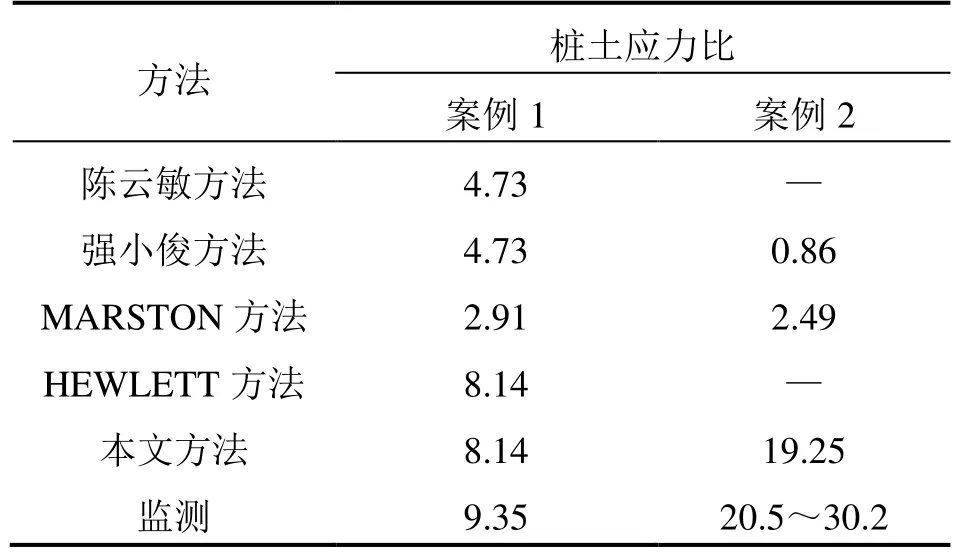
表1 各种方法得到的桩土应力比Table 1 Pile-soil stress ratio obtained by various methods

（2）案例2

文献[16]中广州西二环南段高速公路 K32+065附近路堤高6 m，采用CFG桩正方形布置，桩间距为2.2 m。CFG桩桩顶设置一直径70 cm的圆形盖板，褥垫层采用0.5 m厚的中粗砂，褥垫层顶部铺设一层TGSG20-20型双向拉伸格栅，延伸率不大于11%，抗拉强度不小于20 kN/m。褥垫层以上填筑黏性土。实测桩土沉降差、荷载集度、桩帽顶面处桩土应力比见图3。

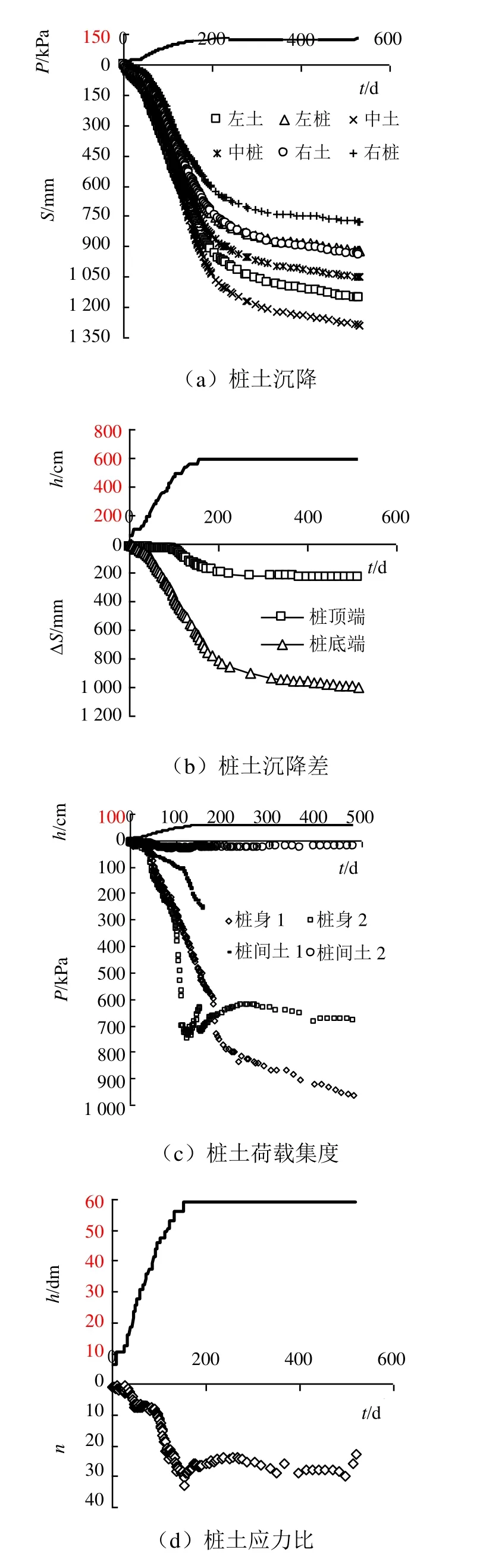
图3 监测结果Fig. 3 Monitoring results

根据桩土沉降差可得到土工格栅向桩帽转移约10.2 kN，剔除其影响后，填土高5.8 m时桩帽顶面处桩土应力比为 20.5～30.2。中粗砂内摩擦角取35°，黏聚力取0 kPa。虽然本工程沉降达到1.25 m，但是拱顶仍位于地下水位以上，因此黏性土内摩擦角取20°，黏聚力取25 kPa。中粗砂和黏性土的重度均取20 kN/m3。采用各种方法得到的桩土应力比见表 1。由于桩底端桩土沉降差较大，MARSTON方法按照摩擦桩计算。本工程拱顶为黏性土，陈云敏方法、HEWLETT方法不适用。可见，本文方法计算的桩土应力比更接近实测值。

3.2 计算方法对比

（1）利用工程实例对比

由3.1节工程实例可知，MARSTON方法计算结果严重偏低，强小俊方法计算结果不合理，HEWLETT方法只适用无黏性土路堤，本文方法适用范围广、且计算结果更接近工程实测值。

（2）利用工程算例对比

由于陈云敏方法已列入公路行业规范[15]，下面主要对陈云敏方法与本文方法进行对比。

刚性桩正方形布置，桩间距取 2.4 m，桩帽边长为1.2 m，路堤土重度为20 kN/m3。路堤填料采用内摩擦角为 35°的无黏性土。本文方法和陈云敏方法的计算结果见图4。图4（b）中分别计算了内摩擦角为30°、35°时的桩土应力比。

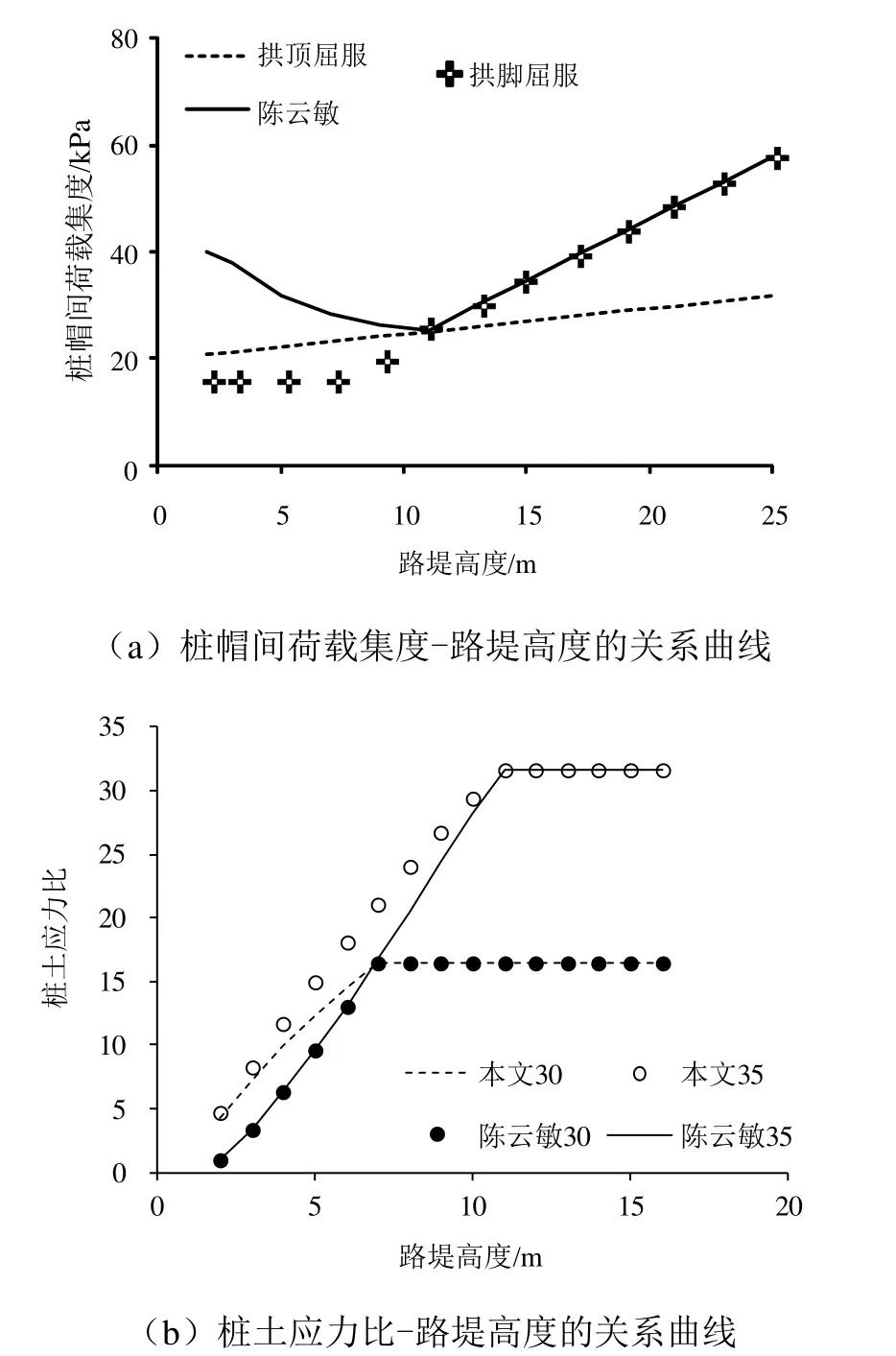
图4 不同方法计算结果对比Fig. 4 Comparison of calculation results of different methods

由图4（a）可知，路堤高度小于10.86 m时拱顶屈服，路堤高度大于10.86 m时拱脚屈服。当拱脚屈服时，本文方法与陈云敏方法计算桩间土荷载集度相同。当拱顶屈服时（路堤高度小于10.86 m），本文方法计算的桩间荷载集度随路堤高度增大而增大，陈云敏方法计算的桩间荷载集度随路堤高度增大而减小。大量工程实测结果表明桩间荷载集度随填土高度增大而增大[8-13]。因此，陈云敏方法计算的桩间荷载集度与实测结果不符。

由图4（b）可知，路堤高度小于6.94 m时，按照陈云敏方法计算的桩土应力比不随内摩擦角变化，违反了抗剪强度随内摩角增大的常识。按本文方法，拱顶屈服时桩土应力比随内摩擦角增大而增大，与付海平等[17]、杨庆年等[18]的研究结论相同。路堤高度为2 m时，陈云敏方法计算的桩土应力比为1.0，明显不合理。

（3）理论

对拱顶为无黏性土的路堤，由于无黏性土等黏聚力等于零，当桩间土沉降导致拱下土体对拱顶反力为零时，拱顶在切向力作用下必然屈服，因此低路堤土拱也会屈服，不存在文献[6]认为的土拱不屈服的情况。桩顶荷载根据拱顶或拱脚屈服对应的桩帽间荷载集度按照复合地基顶面竖向荷载平衡条件计算得到，不存在文献[6]认为复合地基顶面竖向荷载不平衡的问题。另外，拱顶、拱脚只有某个特定路堤高度下才同时屈服，大部分情况下只有拱顶或拱脚屈服，文献[6]关于拱顶、拱脚屈服程度相同的假设不合理。

综上所述，采用本文方法更合理、适用范围更广，且不需要试算。

4 影响因素分析

本节通过算例分析拱脚填料、拱顶填料、桩帽和连梁对桩土应力比、桩荷载率的影响。

路堤填料重度为20 kN/m3，抗剪强度指标见表2。

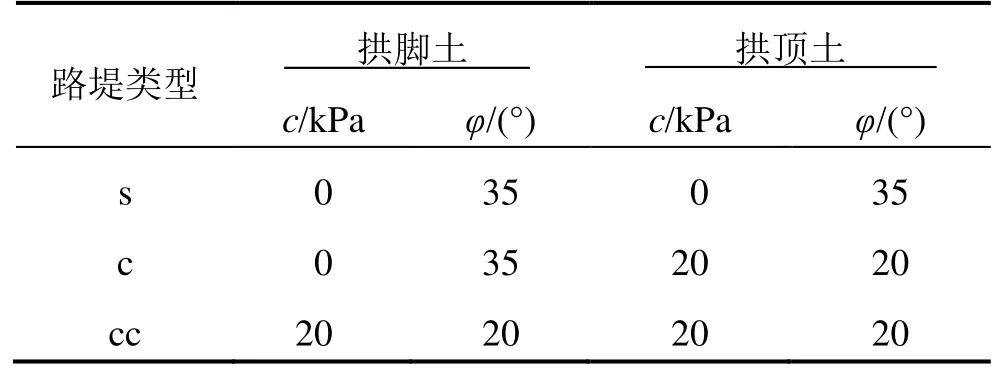
表2 路堤类型与抗剪强度指标Table 2 Embankment types and shear strength indexes

刚性桩正方形布置，桩间距取 2.4 m，桩帽边长为 1.2 m，连梁面积与桩帽面积相等。桩帽（连梁）间荷载集度、桩土应力比、桩荷载率与路堤高度的关系见图5～8。

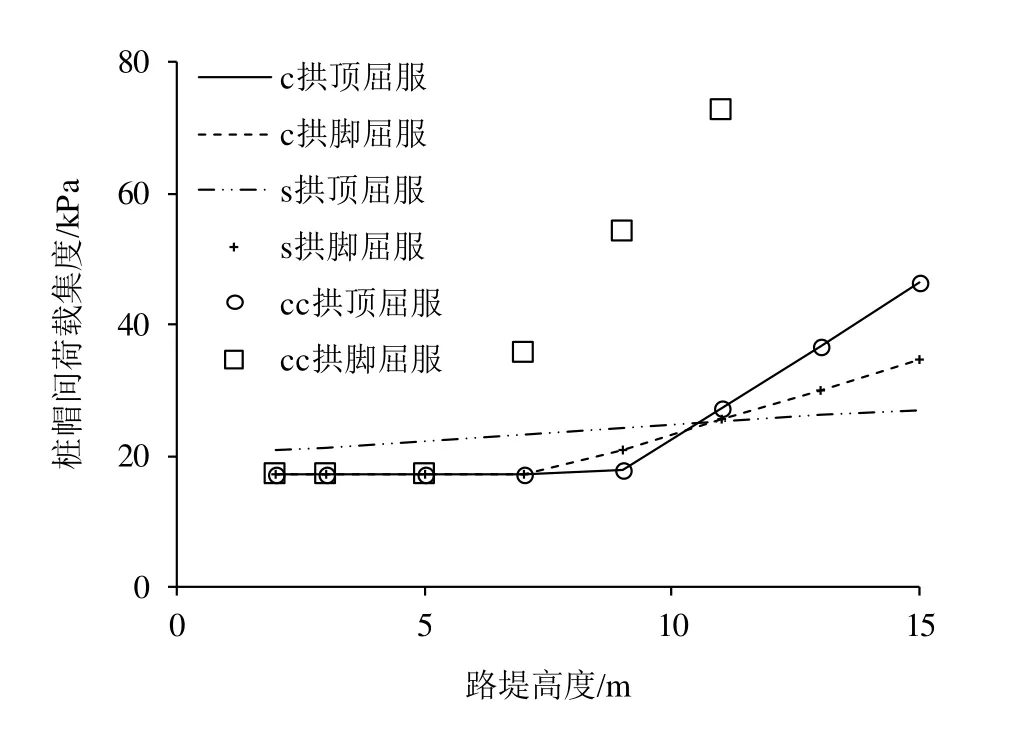
图5 桩帽间荷载集度-高度关系曲线Fig. 5 Relationship curves of load concentration between pile caps and embankment height

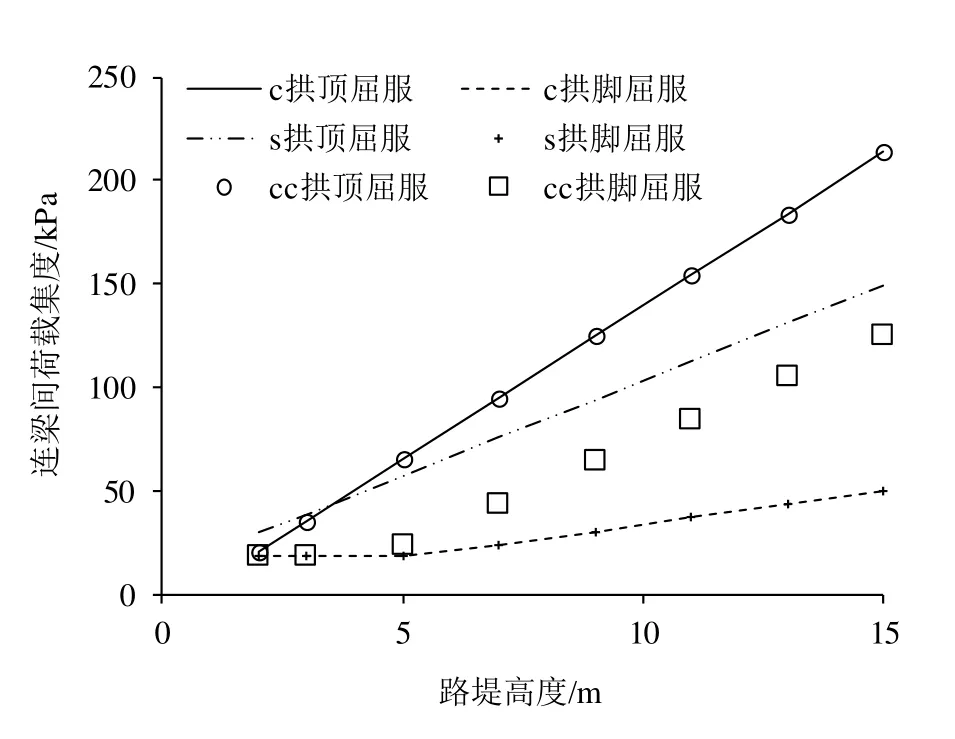
图6 连梁间荷载集度-高度关系曲线Fig. 6 Relationship curves of load concentration between coupling beams and embankment height

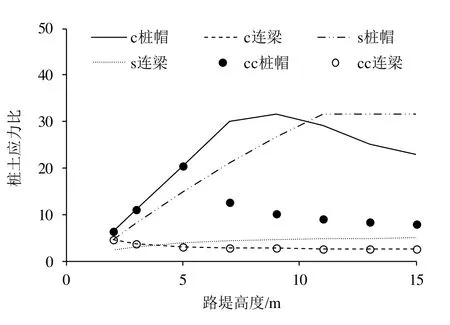
图7 桩土应力比-高度关系曲线Fig. 7 Relationship curves between pile-soil stress ratio and embankment height

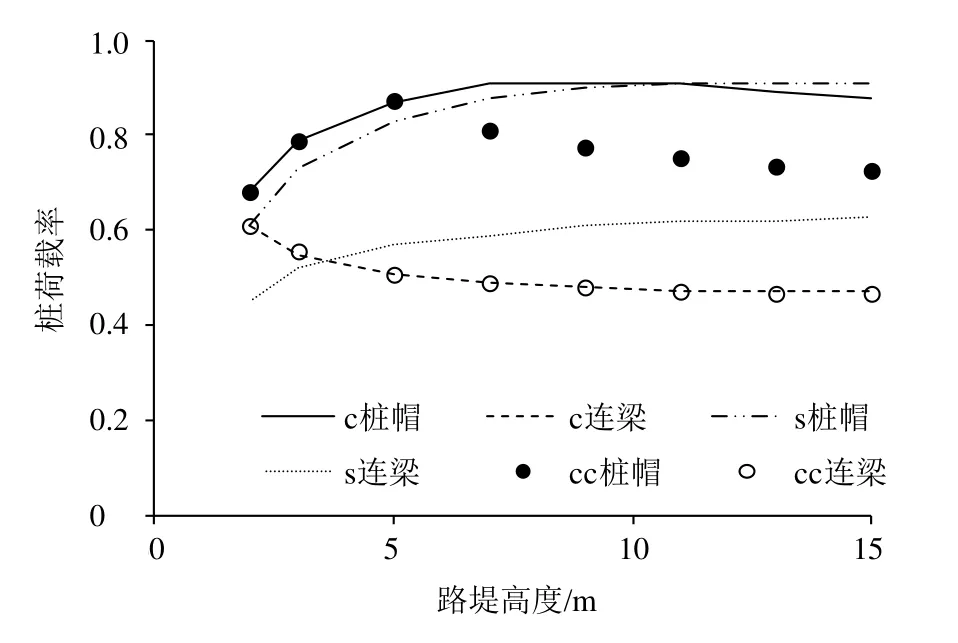
图8 桩荷载率-高度关系曲线Fig. 8 Relationship curves between pile load rate and embankment height

由图5～8可知：

（1）对桩帽复合地基

a）对s型路堤，桩帽上路堤高度小于7 m时，拱脚屈服对应的桩帽间荷载集度不随路堤高度变化，说明拱顶脱空时拱脚也不屈服。桩帽上路堤高度小于10.86 m时，拱顶屈服对应的桩帽间荷载集度大于拱脚屈服对应的桩帽间荷载集度，拱顶屈服，桩土应力比随桩帽上路堤高度增大而近似线性增大，桩荷载率随桩帽上路堤高度增大而增大。桩帽上路堤高度等于10.86 m时，拱顶屈服对应的桩帽间荷载集度等于拱脚屈服对应的桩帽间荷载集度，拱顶、拱脚同时屈服。桩帽上路堤高度大于10.86 m时，拱顶屈服对应的桩帽间荷载集度小于拱脚屈服对应的桩帽间荷载集度，拱脚屈服，桩土应力比、桩荷载率不随路堤高度变化。

b）对c型路堤，桩帽上路堤高度小于7.38 m时，拱脚屈服、拱顶屈服对应的桩帽间荷载集度均不随路堤高度变化，土拱不屈服，桩土应力比随桩帽上路堤高度增大而线性增大，桩荷载率随桩帽上路堤高度增大而增大。路堤高度介于7.38～10.20 m时，拱脚屈服对应的桩帽间荷载集度大于拱顶屈服对应的桩帽间荷载集度，拱脚屈服，桩土应力比、桩荷载率随桩帽上路堤高度增大而增大。桩帽上路堤高度等于10.20 m时，拱脚屈服对应的桩帽间荷载集度等于拱顶屈服对应的桩帽间荷载集度，拱顶、拱脚同时屈服。路堤高度大于10.20 m时，拱顶屈服对应的桩帽间荷载集度大于拱脚屈服对应的桩帽间荷载集度，拱顶屈服，桩土应力比、桩荷载率随桩帽上路堤高度增大而减小。

c）对cc型路堤，桩帽上路堤高度小于4.99 m时，拱脚屈服、拱顶屈服对应的桩帽间荷载集度均不随路堤高度变化，土拱不屈服，桩土应力比随桩帽上路堤高度增大而线性增大，桩荷载率随桩帽上路堤高度增大而增大。路堤高度大于4.99 m时，拱顶屈服对应的桩帽间荷载集度小于拱脚屈服对应的桩帽间荷载集度，拱脚屈服，桩土应力比、桩荷载率随桩帽上路堤高度增大而减小。

d）路堤较小时，拱顶为黏性土的路堤桩土应力比大于拱顶为无黏性土的路堤桩土应力比。

（2）桩梁复合地基

a）对3种类型路堤，拱顶屈服对应的桩帽间荷载集度均大于拱脚屈服对应的桩帽间荷载集度，即均是拱顶屈服。

b）s型路堤的桩土应力比、桩荷载率随连梁上路堤高度增大而增大，且增速逐渐减小。

c）c型路堤与 cc型路堤的桩土应力比、桩荷载率相等。桩土应力比、桩荷载率随连梁上路堤高度增大而减小，且减速逐渐减小。

（3）对相同填料的路堤，采用桩帽复合地基的桩土应力比、桩荷载率均远大于桩梁复合地基的桩土应力比、桩荷载率，性价比更高。

5 结 论

本文推导了可以考虑填料黏聚力的桩土应力比计算模式，研究表明本文方法适用各种填料的路堤，计算结果与工程实测结果接近。分析比对和案例验证表明：

（1）拱顶、拱脚填料种类对桩土应力比均有影响，不同填料的路堤桩土应力比大小及其变化规律不同。

（2）桩土应力比根据土拱屈服位置的受力分析确定，不需要试算。对无黏性路堤宜采用HEWLETT公式。

（3）复合地基刚性桩桩顶设置桩帽的性价比高于桩顶设置连梁。