土工击实试验数据处理的解决方案
2022-05-20许小健
许小健
(芜湖市勘察测绘设计研究院有限责任公司,安徽 芜湖 241001)
0 引 言
土木工程中的建筑地基处理、基槽回填、公路路基修筑、试验检测等,常遇到填土压实问题,而击实试验用规范标准化的方法模拟了工程现场夯实原理,实现了对土的含水率与干密度关系的确定,从而为设计和施工提供依据[1]。因此,如何快速、便捷地确定击实试验成果,具有重要实际工程意义。
目前,《土工试验方法标准》(GB/T 50123—2019)和《公路土工试验规程》(JTG 3430—2020)中均采用图解法确定击实试验成果。众所周知,图解法的优点是工程技术人员可以在图上直观了解试验数据情况,是“规范”规定的方法,容易被工程技术人员所接受;缺点是作图过程具有任意性,不同的人员绘制曲线和利用关系曲线图读取最大干密度和最优含水率的结果受人为影响而具有不确定性。因此,寻求一种方便快捷、客观可靠的试验数据处理方法是非常必要的。当前,除作图法外,广大学者与工程技术人员对击实试验数据处理方法的研究主要有两类,一是拟合法[2-4],二是数值分析法[5-8]。前者的研究实质是以多项式为基础利用拟合原理提供拟合解;后者是利用不同插值函数如Lagrange、Hermite、样条曲线插值等数值分析方法处理试验成果。在数据处理的实现手段上,主要采用了Excel[9]、Mathcad[4]、Matlab[10]、Origin[11]、SPSS[12]等商业软件进行数据处理。以上方法不同程度地使得试验数据处理过程得到了改善。为提供一种新的解决方案,本文给出了一种利用VBA(Visual Basic for Applications,简称VBA)结合Excel内部函数和规划求解工具快速自动化处理击实试验数据的解决方案,该解决方案方便、快捷、准确,且能实现绘图成果可视化。
1 基于多项式的拟合模型及求解方案
《土工试验方法标准》(GB/T 50123—2019)和《公路土工试验规程》(JTG 3430—2020)中规定标准击实试验采用作图法,即以干密度为纵坐标,含水率为横坐标,绘制干密度与含水率的关系曲线,再获得曲线上峰值点的纵、横坐标分别为最大干密度ρdmax和最优含水率ωop。
为避免人工处理试验数据,这里将上述规范作图法转换为数学求解问题。一般情况下,对于每组试验的m=5个土样的含水率和干密度击实试验数据(ωi, ρi)(i=1, 2, …, m),可用n次(n=2, 3, 4)多项式曲线模型进行描述,也即:
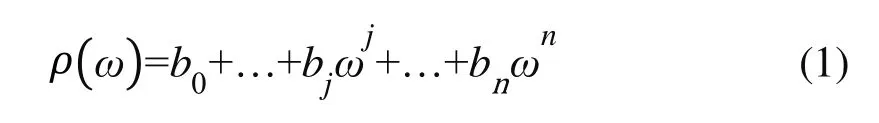
式中:j=1, 2, …, n。为确定多项式曲线模型,需要对多项式系数进行求解,常用的方法是采用最小二乘原理[6-7],即当残差平方和:
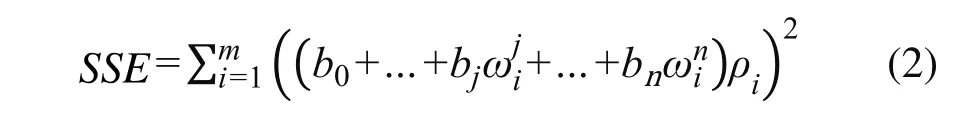
达到最小值时,bj值即为所求多项式系数值。根据求极值方法,此时由式(2)分别对bj求偏导数并令其等于0,然后得到关于bj的线性方程组(也称为法方程),再进行线性方程组求解,从而求得多项式系数bj的值。
“法方程”的求解是确定多项式模型的关键,其求解也稍复杂,可以通过自行编程实现法方程的求解,但对于非计算机专业的工程技术人员来说,用C、C++、Fortran等语言进行编程将面临较大的困难,开发不易。文献[13]虽然采用了VBA编程,但其通过采用矩阵计算求解“法方程”,本质上其编程与采用其他编程语言实现难度无异。鉴于Excel为用户提供了丰富的工作表函数,为简化编程,本文采用Excel内部工作表函数LinEst函数直接实现多项式曲线模型系数的提取,这样可以避免对最小二乘法线性方程组编程求解,从而最大限度地减轻编程的复杂度。LinEst工作表函数通过使用最小二乘法计算与现有数据实现最佳拟合,并返回描述拟合问题的数组,其函数调用语法为LinEst ([yValues],[xValues], [const], [stats]),其调用参数为:(1)yValues为必需参数,xValues为可选参数,对于击实试验来说,分别相当于干密度和含水率的集合;(2)const和stats为可选参数。其中stats用于指定是否返回拟合回归统计值,如判定系数r2、残差平方和SSE等。具体的使用方法可通过参阅Excel帮助文档,也可参考本文后续编程实现部分。
对于多项式拟合模型,一旦其系数确定后,其模型也就确定,但为获得最大干密度ρdmax和最优含水率ωop的值,还需要对模型进行进一步求解。由于多项式模型为高次非线性方程,求解不易,而Excel为非线性问题的求解提供了规划求解工具Solver,使得用户较易获得问题解。非线性规划求解工具Solver采用“Generalized Reduced Gradient (GRG2)”代码,该代码由Leon Lasdon(德克萨斯大学奥斯汀分校)和Alan Waren(克利夫兰州立大学)开发,并由Frontline Systems公司封装后提供。用户无需关心具体的代码,只需编写少量的VBA程序进行简单的调用即可在Excel中实现复杂问题的求解。
综上所述,本文提出的解决方案是通过在Excel中运行VBA程序,先利用Excel内置工作表函数LinEst函数直接提取多项式拟合模型的系数,再调用Excel规划求解工具Solver实现多项式拟合模型的极值求解,从而确定最大干密度和最优含水率。
2 基于Excel VBA的解决方案实现
VBA是一种具有简单易用特点的编程语言,其编程系统中加入了面向对象的机制,把Windows编程的复杂性程序进行了封装,并提供了一种可视界面的设计方法。同时,VBA程序赖以运行的应用程序开发工具VBE(Visual Basic Editor,简称VBE)寄生于Office环境。由于Office软件的安装与使用较为普遍,故VBA的运行和存放也无需特殊的环境设置,这进一步降低了编程开发的门槛。
为方便使用,本文基于Excel设计了程序用户界面,如图1所示,该界面保留了与Excel界面的风格统一和美观。Excel运行时,程序会在Excel的菜单栏形成一个“土工击实试验”菜单项,该菜单项包含相应功能选项。

图1 程序用户界面Fig. 1 Application user interface
上述菜单项的各功能响应均通过VBA程序实现。
3 应用算例
为展示本文解决方案的便捷性和有效性,现以表1中击实试验数据组举例说明。其中test1试验数据来源于文献[7],test2和test3试验数据来源于文献[10],test4试验数据来源于文献[4],test5来源于文献[15]。
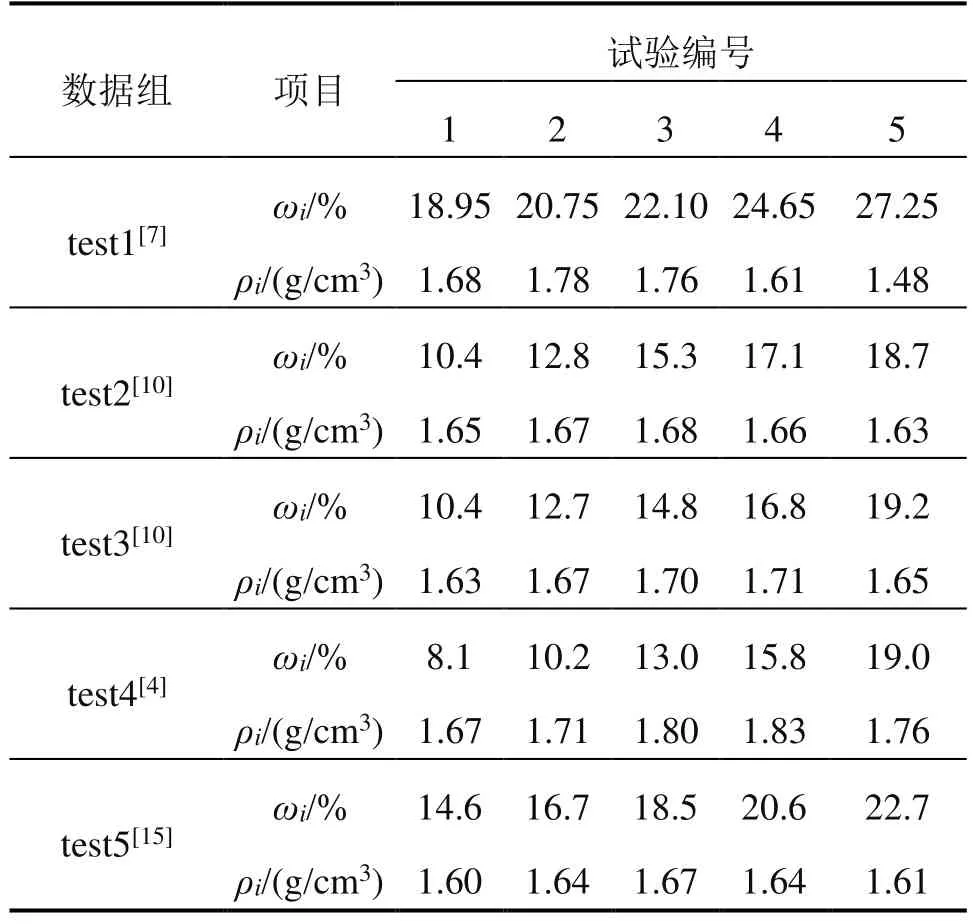
表1 各数据组原始试验数据Table 1 Original test data of each data group set
启动Excel后,默认自动打开图1所示“土工击实试验数据处理”选项卡。以表1中test1为例,在Excel表格的B2:B6单元格内依次输入含水率试验数据ωi,在C2:C6单元格内依次输入干密实试验数据ρi;输入完成后,点击“模型拟合计算与极值求解”,程序会自动批量依次完成n=2、n=3、n=4阶多项式曲线模型的拟合与极值求解工作,并显示结果如表2所示。表2中,Excel表格F~J列中自动填充多项式系数结果;在K和L列分别显示多项式拟合附加回归统计值r2和SSE;在M和N列分别显示最优含水率ωop和最大干密度ρdmax。经过比对,本文处理test1试验数据的结果与文献[7]的4次多项式曲线拟合模型结果完全一致,且与ωop=20.98%,ρdmax=1.781 g/cm3也完全相同。但文献[7]的做法需要在Matlab软件的命令窗口中根据软件反馈信息不断与软件交互输入,便捷性稍差,而本文则实现了在Excel环境中通过一次简单点击操作就能立即显示数据自动化处理结果,操作简单便捷。
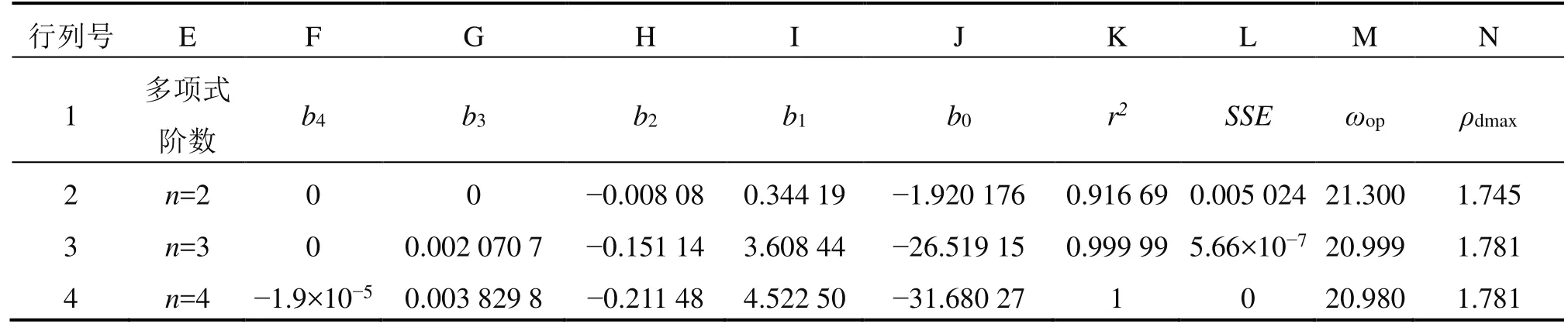
表2 test1数据组的计算结果Table 2 Calculation results of data group set test1
以test2、test3试验组数据为例,为便于讨论,提供求解最大干密度与最优含水率结果见表3。限于篇幅,本文所求各阶多项式曲线模型系数不再展示,后同。由表3可见,本文所得结果与文献 [10]利用Matlab商业软件处理结果相比,也几乎一致,仅test2数据组在多项式阶数较高(n=3、n=4)时所求得含水率精度上略有差异,但最大误差也不超过0.15%,可以忽略不计,其原因是在计算过程中对数据精度的设置差异所致。

表3 各方法所得结果的比较(test2、test3数据组)Table 3 Comparison of results obtained by different methods (data set test2, test3)
再以test4数据组为例,文献[4]中提供了多项式阶数n=3的求解情况,如表4所示。可见,本文处理test4试验数据的结果(n=3阶)与文献[4]采用Mathcad商业软件所得结果完全一致,与《公路土工试验规程》(JTJ 051—93)图解法结果也较为接近。由此可见,本文解决方案便捷、有效。

表4 各方法所得结果的比较(test4数据组)Table 4 Comparison of results obtained by different methods (data set test4)
最后以test5数据组为例,在多项式阶数n=2时,各方法所得结果均较为一致。在多项式阶数n=3、n=4时,文献[15]的Newton迭代计算拟合法所求结果与本文所得结果差异较大,如表5所示。不难发现,对于多项式阶数n=3时,文献[15]中拟合法和数解插值法所求最大干密度1.63 g/cm3和1.59 g/cm3,明显小于击实试验实测数据的1.67 g/cm3,较为不合理。对于多项式阶数n=4时,文献[15]求得最优含水率为14.2%,明显低于其图解法结果18.6%和本文所求结果18.63%,也不合理。为便于观察,利用设计的“导出击实试验成果图”功能模块,绘制n=4时的含水率与干密度关系曲线图如图2中(a)所示,可见文献[15]的ωop=14.2%不符合关系曲线趋势,同样可以得出其不合理的结论。此外,从判定系数r2值来看,本文所求拟合模型效果更好。

表5 各方法求得结果的比较(test5数据组)Table 5 Comparison of results obtained by different methods (data set test5)
为避免产生上述test5所得试验结果偏差较大的情况发生,利用程序可以自动批量绘制、导出含水率与干密度关系曲线图的功能,可以起到辅助用户直观掌握最大干密度和最优含水率情况,同时也可以起到横向验证数据处理结果与成果图所得图解结果一致性的作用。绘图过程无需人工进行调整,保留了图解法的直观。
值得说明的是,本文所提解决方案在处理test4和test5试验数据时,发现当n=4时,Excel规划求解工具Solver容易陷入局部解,所求最大干密度偏低,最优含水率结果易产生变动;而在n=2、n=3时,均未发现此现象。经过多次试验求解发现,这与规划求解工具Solver求解迭代计算的初始值有关。而软件缺乏解决实际问题对初始值的选择,这是软件所采用的计算方法所致。上述文献[15]中所求test5试验组所得不合理结果亦应属此原因所致。为解决这一问题,考虑到含水率的取值要存在合理的实际意义,所以其初值的选择也并非难事,只要将自变量迭代初始调整为试验组含水率数据的平均值即能较好地解决该问题,通过在“模型拟合计算与极值求解”源程序调用规划求解工具Solver时添加cells(4,"M").Formula= "=AVERAGE(B2:B6)"语句即可解决。当然,也可以选择试验数据组已经获取的最大干密度所对应的含水率作为自变量迭代初始值,这也是一种可选择的方案。
此外,值得一提的是,由文中5组试验组数据情况发现,在多数情况下,当多项式阶数为n=2时,拟合效果稍差,如图2(b)中所示含水率与干密度关系图曲线峰值点,其拟合计算所得最大干密度较实测数据偏低。当n=3、n=4时,所求最大干密度与最优含水率的结果更为符合原始数据规律,但n=4时,含水率与干密度趋势曲线的两侧尾部易产生“翘曲”,图2(a)中曲线尾部两端和如图2(c)中曲线左侧尾部所示,n=3时,则容易取得数据成果和所绘制曲线趋势特征的“均衡”,如图2(d)所示。
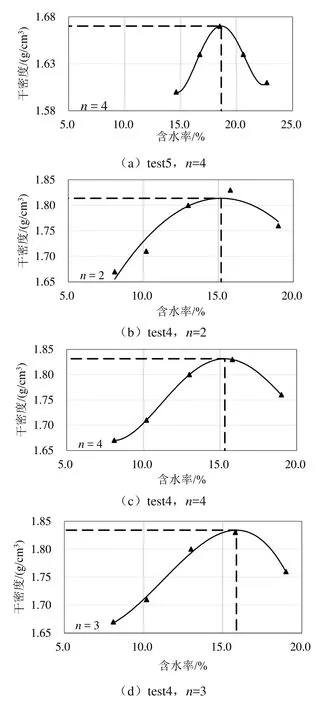
图2 含水率与干密度关系曲线图Fig. 2 Relation curve between moisture content and dry density
4 结 论
(1)基于多项式曲线拟合原理,将图解法转换为数学求解问题,再利用Excel规划求解功能获得击实试验成果的解决方案,克服了人为因素的影响,避免了人工图解法处理试验数据较为繁琐和具有任意性的劣势。
(2)实现了与Excel风格统一的可视化程序界面,程序界面美观、便捷、高效,实现了通过简单点击操作就能进行数据自动化处理和成果图绘制工作。
(3)基于Excel VBA的土工击实试验数据处理解决方案是一种精确、高效、直观的数据处理和图表可视化制解决方案,对于提高试验和工程技术人员的工作严谨性、准确性和效率都有较好的作用;VBA编程门槛较低,值得工程技术人员掌握和学习使用。
