连续梁桥的抗倾覆稳定性设计方法

刘书画

（中国公路工程咨询集团有限公司，北京 100000）

1 引言

连续梁桥因具有良好的受力性能，被广泛应用于基础交通建设中。现有桥梁设计中主要考虑桥梁的强度，而对其抗倾覆稳定性的规定较少。但在汽车超载情况下容易因抗倾覆稳定性不足而导致交通事故的发生。因此，本文针对连续梁桥抗倾覆破坏进行研究。

2 荷载工况

2.1 永久作用

永久作用考虑的要素较多，此处对较为关键的几项展开分析：（1）箱梁自重：根据断面展开计算，以混凝土为例，此类工程材料的重度为25 kN/m3；（2）支座沉降：单个墩台最大沉降量取5 mm；（3）铺装层及护栏的荷载：前者层重47.8 kN/m，后者单侧重6.2 kN/m；（4）收缩徐变：考虑10 a的收缩徐变。

2.2 可变作用

可变作用的关键要素因素有3项，具体做如下分析：（1）移动荷载。根据JTGB 01—2014《公路工程技术标准》中公路-Ⅰ级车道荷载验算，同时需要考虑到计算荷载的冲击系数，以保证参数的合理性。（2）整体升降温荷载。结构的温度存在变化，其中，整体升温、降温幅度均一致，取18.5℃。（3）温度梯度荷载。对于此项指标的选择，主要参照JTG4 D60—2015《公路桥涵设计通用规范》第4.3.12条。

2.3 荷载组合

在桥梁工程中，荷载组合需要成为荷载工况分析中的重点考虑对象，主要参照JTG D60—2015《公路桥涵设计通用规范》第4.1.5条，具体涉及两方面，即基本组合和标准组合。

3 连续梁桥抗倾覆稳定性分析

3.1 抗倾覆轴线

连续梁桥易在汽车荷载和偏载等作用下出现倾覆。在反倾覆设计时，首先需确定倾覆轴，具体至连续梁桥中，则围绕两部分做针对性的考虑：直线段，倾覆轴以桥梁中线最外层的支座线为宜；曲线段，其倾覆轴较为复杂，假想倾覆轴如图1所示。

图1 假想倾覆轴

3.2 工况的确定

立足于桥梁的实际运营模式，确定4种荷载模式或称4种工况：（1）工况1为公路-I级汽车荷载，模拟标准设计荷载；工况2为1.3倍公路-I级荷载，模拟一般汽车超载；工况3为55 t重车（10 m间距），模拟重车车队；工况4为3倍公路-I级荷载，模拟严重超载。

3.3 各工况的支座反力分析

相比于直线段，连续梁桥曲线段的受力体系更为复杂，无论荷载作用形式发生何种变化，均有不同程度的弯矩-偶合作用。部分曲线段采用的是单支座的支承方式，受支座结构方面的限制，其平衡效果远不及双支座，若存在较大的反力差，则会伴有负反力以及脱空的情况，随之作用于桥梁整体结构，偏载的出现使连续梁桥发生倾覆。在荷载持续增加的情况下，迫使桥梁内、外侧受力状况显现出明显的差异（内侧反力降低，外侧支座反力有持续增加的变化）。若以成倍的方式快速增加外荷载，支座反力将加大，内侧支座反力受到偏载的影响而有下降的变化。

对比分析各部分结构的反力可知，中墩支座和桥梁外侧支座的该值处于较大的水平[1]。基于支座反力法展开抗倾覆稳定性分析，认为在前述所提的4种工况下，桥梁内侧支座均无负反力，也不会出现脱空的情况，由此进一步推测，该连续梁桥不存在倾覆破坏的可能。

3.4 抗倾覆稳定性

仅采用支座反力法难以准确地判断连续梁桥的抗倾覆稳定状态，为规避该方法的局限性，此处引入抗倾覆稳定系数，通过该指标的应用，围绕抗倾覆稳定性展开分析。

各荷载模式下的抗倾覆稳定系数如图2所示。随着荷载作用的增加，内部支座有明显的收缩变形，除此之外无其他异常状况（未见脱空）。受超载和偏载的影响，桥梁的抗倾覆能力减弱[2]。较之于前述所提的支座反力法，抗倾覆稳定系数的引入具有更为突出的参考价值，可作为判断桥梁横向稳定性的关键依据。

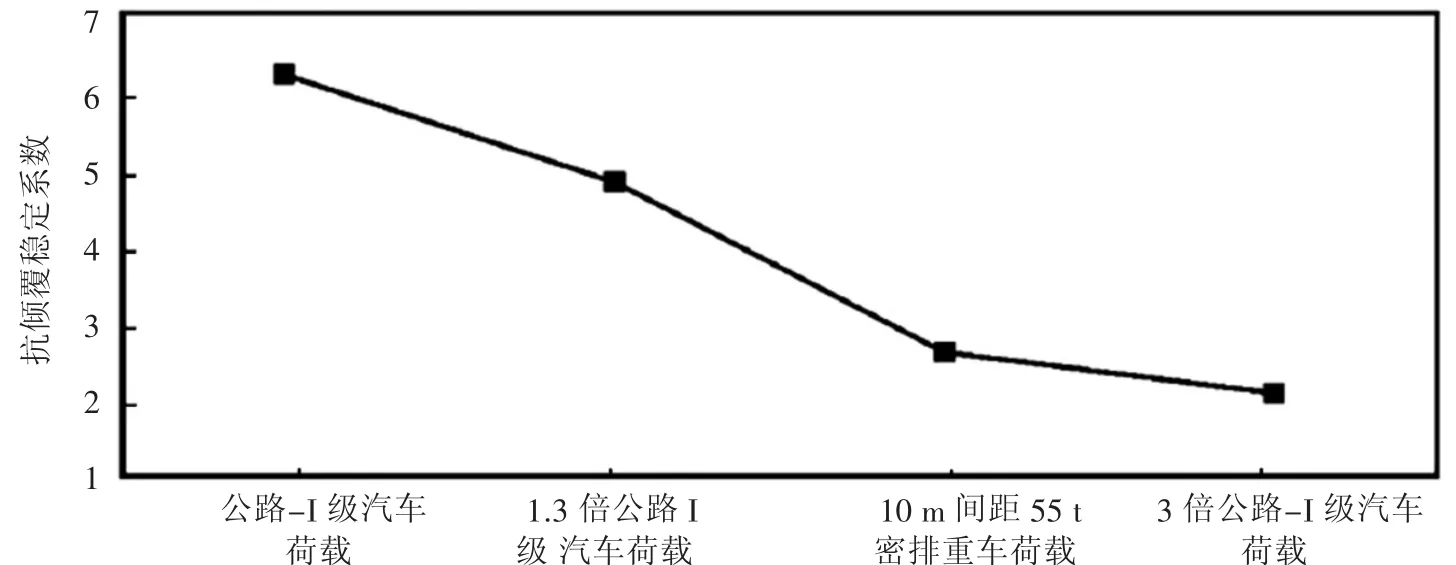
图2 各荷载模式下的抗倾覆稳定系数

桥梁发生倾覆失稳的原因较多，其中，因荷载作用而产生的不平衡力矩为主导因素。根据作用关系，稳定力矩与上倾覆力矩的比值在很大程度上影响了桥梁的横向稳定性，通常该比值需在2.5以上，此时有利于维持桥梁的横向稳定性。在所提的各类工况中，公路-Ⅰ级荷载所对应的倾覆稳定系数最大，达到6.1，远超过2.5。各桥梁支座均保持工作状态，在正常荷载作用条件下，其均能稳定使用，抗倾覆稳定性得到保证。

考虑桥梁运营时的超载条件，围绕工况4进行模拟分析，发现此时的抗倾覆稳定系数较小，仅为2.1，并未达到2.5的下限值要求，尽管其在超载时无强度破坏问题，但就横向抗倾覆稳定性而言达不到要求，安全性与可靠性相对较差。对于工况2而言，抗倾覆稳定系数约与工况3的抗倾覆稳定系数相同，但从工况3的分析结果来看，桥梁具有抗倾覆稳定性，且并无统一的荷载验算标准，因此，易在设计中趋于保守，出现桥梁稳定可靠但其经济效益优势受到抑制的局面（材料投入较多等）。综合考虑前述所提的情况，提出抗倾覆稳定性荷载验算的工作思路，即应用可靠度理论，并紧扣桥梁的实际交通状况，展开更为客观的分析。

3.5 支座预偏心对抗倾覆稳定性的影响

在弯扭-偶合作用下，连续梁桥曲线段的受力条件更为复杂，且尤为特殊的是独柱墩支撑体系，其支座容易因多重力的作用（包含压力、扭矩）而处于异常使用的状态。为切实改善桥梁的受力状况，应当有效布置支座，充分发挥该装置在抗倾覆稳定性领域的作用。并且，支座的布置位置还会对桥梁的倾覆轴带来影响。支座预偏心的出现会随之导致抗倾覆稳定性发生变化，为明确具体的作用关系，此处采用参数控制法加以分析。以连续梁桥曲线段的独柱墩为主要考虑对象，调整支座预偏心的值，构建有限元模型，探寻预偏心与结构抗倾覆稳定性所具备的关联，抗倾覆稳定系数与偏心距的关系如图3所示。

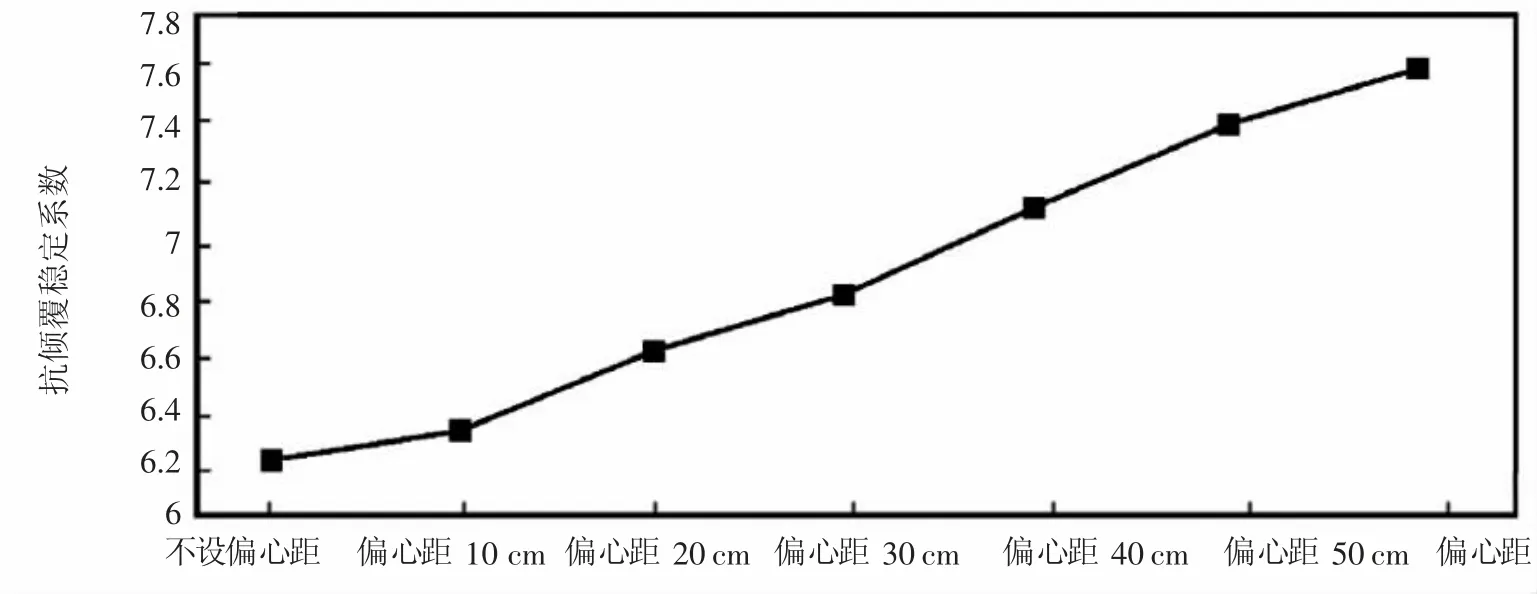
图3 抗倾覆稳定性系数与偏心距的关系

偏心距发生变化后，桥梁支座均不存在空隙，达到要求。各类支座在偏心距发生变化时所受到的影响不尽相同，内侧支座则对偏心距的变化较为敏感，其反作用力在偏心距增加时也同步加大[3]。由此看来，支座的受力状态与偏心距有密切关联，而为了优化支座的受力条件，可对偏心距做合理调整。从抗倾覆稳定性的角度来看，因偏心距的增加，此方面的性能得以增强。根据前述分析结果，认为在独柱墩处设置偏心距较为合适，其在改善内外侧支座的受力条件方面具有积极意义，而支座受力状态的稳定性又会带来抗倾覆稳定性能的提升，综合效果较佳。

4 连续梁桥设计阶段的抗倾覆措施

曲率半径、桥面宽度等是影响抗倾覆能力的关键因素，在设计阶段需要做充分的考虑：

1）设计中控制好支承间距，适当增加支承与箱梁下缘的距离，但必须保证支承边与箱梁下缘的最小距离达到要求。通过对支承间距的有效控制，减小支座脱离受压状态的影响，提高箱梁的抗倾覆性能，使结构具有更为突出的稳定性优势。

2）合理设计桥梁线形，特殊地段设缓和曲线，在此前提下，进一步考虑微弯桥的抗倾覆性能，由于该类桥梁结构缺乏足够的抗倾覆性能，因此，必须以合理的方式规避。例如，优先选择曲率较小的桥型，此时对于保证桥梁的抗倾覆稳定性具有重要作用。

3）独柱墩设计中，适当设置偏心距，发挥偏心距在优化结构受力方面的作用，提升桥梁的抗倾覆稳定性。

4）对于支座支承的箱梁桥，在设计时应当考虑到独柱墩单支座支承的数量，正常情况下每2跨设1个双支座支承，具体根据实际情况而定，但不宜连续设置3个或更多的独柱墩单支座支承，否则反而会影响结构的抗倾覆性能。

5）桥梁越窄，其抗倾覆稳定性越高，根据此规律可知，在宽桥的设计中宜采用双柱墩支承，该类型的结构具有较突出的抗倾覆能力。

6）设计中，还需有效避免单向受压支座脱离受压状态的情况，而为了达到此方面的要求，可从支座的结构形式以及受力特性出发，配套稳定可靠的传递拉力装置。

5 结语

随着荷载的增加，桥梁支座无脱空现象，但内侧支座反力表现异常，有逐渐脱空的变化特点；在各类工况中，工况4时桥梁的抗倾覆稳定性能不达标，因此，就此方面做深入考虑，紧密结合桥梁的实际运营情况，组织桥梁抗倾覆荷载验算工作；偏心距的合理性是保证桥梁抗倾覆稳定性的关键前提之一，在设计中应着重考虑偏心距的控制，以30 cm的偏心距为宜，此时桥梁内外侧的支座可达到相对均衡与稳定的状态。