植被指数最佳地理轴线研究

2022-05-20姜欣彤周祖昊严子奇

人民黄河 2022年5期

姜欣彤，周祖昊，黎曙，庞亮，严子奇

（1.中水珠江规划勘测设计有限公司，广东广州 510610；2.中国海洋大学工程学院，山东青岛 266100；3.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；4.黄河水利委员会西宁水文水资源勘测局，青海西宁 810008）

1 引言

在地形复杂、高程差异显著的高原山区，植被的空间分布格局具有明显的特点。有学者发现高原山区的植被分布受高程影响，植被指数（NDVI）空间分布具有明显的垂向条带性特征。如陈菁［1］对植被垂直分布空间格局进行研究，并以位于四川省西南部的邛崃市为例探究植被与高程带之间的关系，结果表明不同高程带内植被分布具有差异性；Li等［2］针对喜马拉雅山东部雅鲁藏布江流域内NDVI沿海拔梯度的分布模式进行分析，发现NDVI在海拔3 000 m附近区域内达到最大；刘晓婉等［3］对雅鲁藏布江流域NDVI的空间分布特征进行分析，发现该流域内NDVI与高程具有相依性，总体呈现随高程提高而减小的趋势。另有学者研究发现高原山区的植被分布除受高程影响外，地理要素也是其变化的影响因子，NDVI空间分布具有明显的水平地带性特征。如赵建军［4］将阿帕拉契亚山NDVI分别与高程和地理因子的相关关系进行分析，研究表明高程和经纬度均影响NDVI空间分布，该区域内高程每升高100 m，其NDVI下降0.006 2个单位，纬度每向北移动1°NDVI下降0.01个单位；张文江等［5］在对青藏高原中东部NDVI空间分布格局进行分析时发现，青藏高原呈现独特的三维地带性特征，在3 500 m高程以下NDVI与纬度相关关系较强，而3 500 m以上NDVI与经度相关关系更强；赵健赟等［6］对青海高原植被空间分布特征进行研究发现，研究区内NDVI与经度有明显的正相关关系，与纬度有明显的负相关关系，NDVI分布有明显的水平地带性特征。

纵观前人针对高原山区植被空间分布特征的研究，大都聚焦于NDVI与高程、经度和纬度的相关关系上，以此说明NDVI具有垂向条带性和经纬向地带性。但是，在地形条件复杂的高原山区，植被指数并非严格按照经度或纬度的方向呈现条带性变化趋势，或许是沿着某一方向表现出显著的条带性分布特征，因此单用高程或经纬度作为指标难以定量描述。笔者在前人研究的基础上，将经纬度作为组合因子，提出植被指数空间变化最佳地理轴线的概念，即在此方向上，植被指数的空间分布具有最显著的条带性特征，以此深入探究高原山区的植被指数空间分布条带性变化规律。

位于黄河干流唐乃亥水文断面以上的黄河源区，集水面积仅占黄河流域面积的16.2%，但径流量却占黄河流域总径流量的三分之一，故有黄河的“水塔”之称［7］。黄河源区位于青藏高原东北部，因特殊的地理位置和气候特征，其生态环境质量对下游地区的生态环境有重要的影响，因此对黄河源区植被空间分布规律进行研究具有重要意义。幅员辽阔、地形复杂的黄河源区植被空间分布格局遵循怎样的规律？地理因子如何影响黄河源区植被空间分布格局？造成黄河源区植被空间分布格局的机制是什么？本文将从最佳地理轴线的角度出发，揭示黄河源区植被指数的空间分布条带性变化规律，并对其形成如此空间格局的原因作出合理解释。

2 研究区概况及数据

黄河源区地理坐标范围为北纬32°09′—36°34′、东经95°54′—103°24′，总面积约为13万km2。总体地形特点主要为起伏和缓的丘状高原，区域内地势西北高、东南低。其中分布有峡谷、高山、盆地、冰川等地貌，西部和中部地势高，最高处位于阿尼玛卿山，最低处位于龙羊峡，海拔在2 409～6 254 m之间（见图1）［8］。源区内自然环境类型多样，高寒植被分布广泛，约占源区面积的3／4。主要的植被生态类型包括高寒草甸、高寒草原、高寒沼泽、高寒灌丛、常绿针阔叶林等［9］。

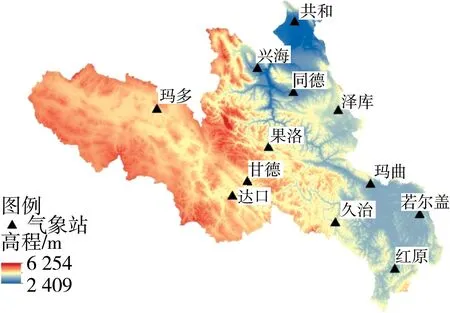
图1 黄河源区高程及气象站

本研究采用的数据如下：①美国NASA航天中心发布的MOD13Q1归一化植被指数，时间分辨率为16 d，空间分辨率为1 km，数据选用年份为2003—2017年；②中科院地理空间数据云网站下载的数字高程（DEM）数据，空间分辨率为30 m；③基于研究区内12个气象站通过反距离权重法空间插值后再进行高程修正的气温、降水量逐月数据，将2003—2017年每年逐月降水量求和作为年降水量，逐月气温求平均作为年气温。

结合MRT技术、ArcGIS及MVC法对MOD13Q1遥感数据产品进行处理，得到NDVI值。通过MRT技术可以对遥感影像进行拼接和重投影处理，并提取NDVI波段。利用ArcGIS掩膜工具提取研究区范围，利用栅格计算工具将原始NDVI资料从-10 000～10 000的浮点数转化为-1～1之间的标准NDVI值。本文在计算时只考虑有植被的区域，因此将栅格中河流、湖泊、岩石和裸土等NDVI值小于0的非植被区域像元设置为空值以剔除。MVC法是目前国际上通用的最大化合成法［10］，即将每月内的NDVI数据取最大值进行像元合成，以此消除云、大气和太阳高度角的部分干扰［11］。将通过MVC法进行像元合成后的NDVI作为月NDVI值。植被生长季为4—10月，本文将每年4—10月NDVI值计算平均值作为该年植被生长季NDVI，得到研究区2003—2017年15幅生长季NDVI空间分布图，再计算15 a植被生长季NDVI多年平均值，以此为数据基础研究黄河源区植被指数空间分布规律（见图2）。采用ArcGIS工具在研究区内等间距选取1 990个样本点，提取样本点位置所在经纬度和15 a植被生长季平均NDVI值。

图2 黄河源区植被指数空间分布规律

3 最佳地理轴线计算方法及原理

本文提出最佳地理轴线的概念，即将经度和纬度作为组合因子，定义一种新的坐标系，定义方法为：从地理平面上选定一个原点，从原点向不同角度作极轴，计算样本点xi在轴线上的投影距离Di。对于每一角度的轴线，可建立样本点NDVI值与样本点在此轴线上投影距离D的回归关系并计算决定系数R2，R2最大值对应的轴线即为“最佳地理轴线”，沿着此轴线方向，植被指数空间分布呈现显著的条带性变化趋势。

将经线、纬线分别作为横纵坐标，单位为度。以横坐标大于所有样本点经度最大值、纵坐标小于所有样本点纬度值为原则选取一个原点。从原点向研究区内做不同角度射线，作为地理轴线，将经线记作K1，纬线记作K2，穿过研究区内部的轴线记作Ki。将研究区内所有样本点NDVI值与样本点在轴线Ki上的投影距离D建立回归关系，并计算决定系数R2。

决定系数R2也称为拟合优度，它表征回归方程在多大程度上解释了因变量的变化，即表征因变量NDVI的变异中有多少可由控制的自变量投影距离D来解释。其计算公式为

式中：SSE为残差平方和；SST为总离差平方和；y为样本点观测值；ˉy为样本点均值；＾y为根据拟合回归关系得到的样本点拟合值。

R2的取值范围为0～1，R2越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比越高，观察点在回归直线附近越密集。对于样本点NDVI值与投影距离D的回归关系，R2越高，表明对于同一投影距离D，NDVI分布越密集。过原点做半径为D的圆，过不同角度的轴线（Ki）与圆的交点做切线（ti）。由于该切线上所有样本点在轴线上的投影距离都为D，因此若此条切线上NDVI分布较散乱、大小不一，拟合NDVI值与样本点NDVI值残差平方和就会大，导致回归模型决定系数R2变小；若此条切线上样本点NDVI值分布较集中，样本点NDVI值在回归线附近密集，则决定系数R2就大。选择R2最大值对应角度的轴线作为最佳地理轴线，表明在此轴线的垂线方向上NDVI分布范围较为集中，沿此轴线NDVI空间分布具有明显条带性变化规律。

4 分析与讨论

以黄河源区NDVI为例，计算其最佳地理轴线，如图3所示。把研究区NDVI值划分为＜0.2（蓝）、0.2～0.4（红）、0.4～0.6（绿）和＞0.6（紫）4个区间，将样本点所在经纬度和NDVI值做气泡图。由图3可知，研究区NDVI值从东南向西北方向递减。以（103.5°，31.5°）为原点，从该原点出发分别把斜率k在tan 90°～tan 180°范围内的每一度轴线作为地理轴线，建立样本点NDVI值与每条轴线上投影距离D的回归关系并计算决定系数R2和均方误差MSE，并对决定系数的显著性进行F检验。

图3 黄河源区植被指数最佳地理轴线计算

不同角度轴线样本点NDVI值与轴线上投影距离D回归关系如图4所示。R2、F统计值和回归模型的均方误差MSE随角度变化规律如图5所示。

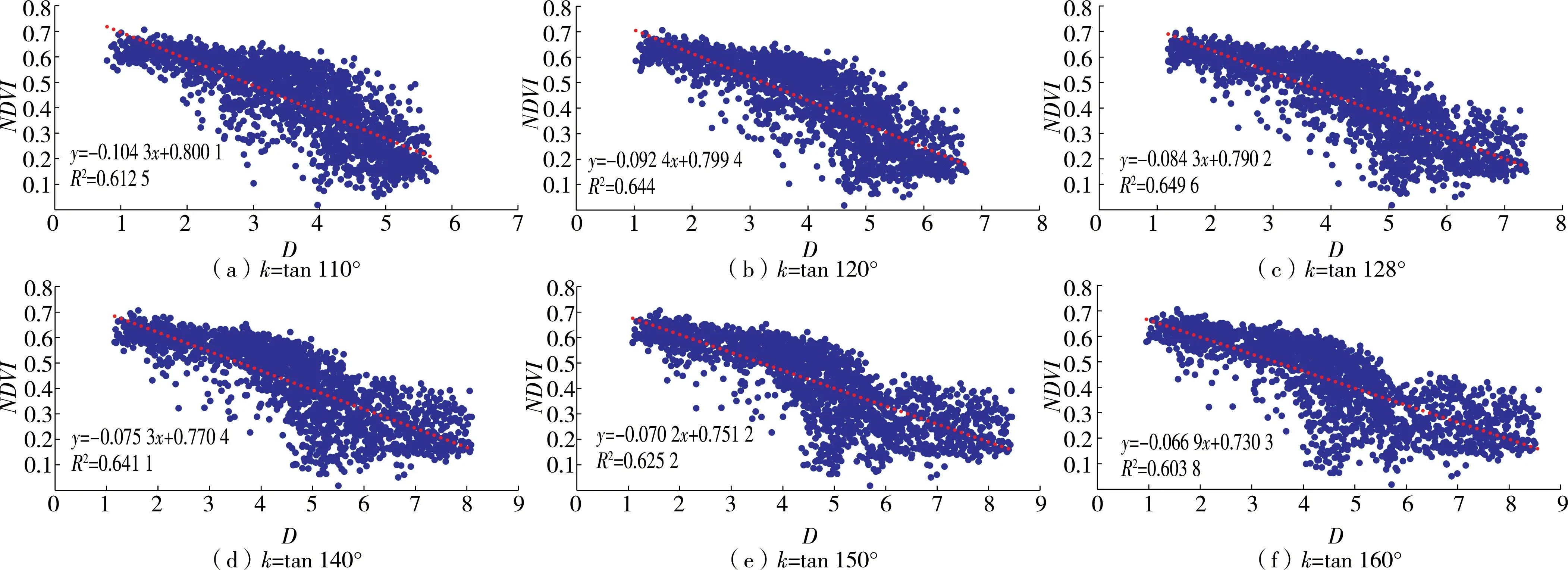
图4 不同角度轴线样本点NDVI值与投影距离D回归关系

从与x轴正方向夹角90°（经线）到夹角180°（纬线）内的每一度轴线，NDVI与投影距离的回归模型均通过了0.05显著性水平F检验，这说明地理因子对黄河源区NDVI确实有显著影响。由图5可知，当轴线与x轴正方向夹角为128°，即西偏北52°时，NDVI与此轴线上的投影距离回归关系最佳，R2达到0.649 6，此时回归模型的F统计值最大，MSE最小，在此方向上，NDVI在拟合回归线附近分布较密集，同一投影距离上NDVI分布较为集中，即在此方向上NDVI具有明显的条带性，因此西偏北52°为研究区NDVI空间分布的最佳地理轴线。

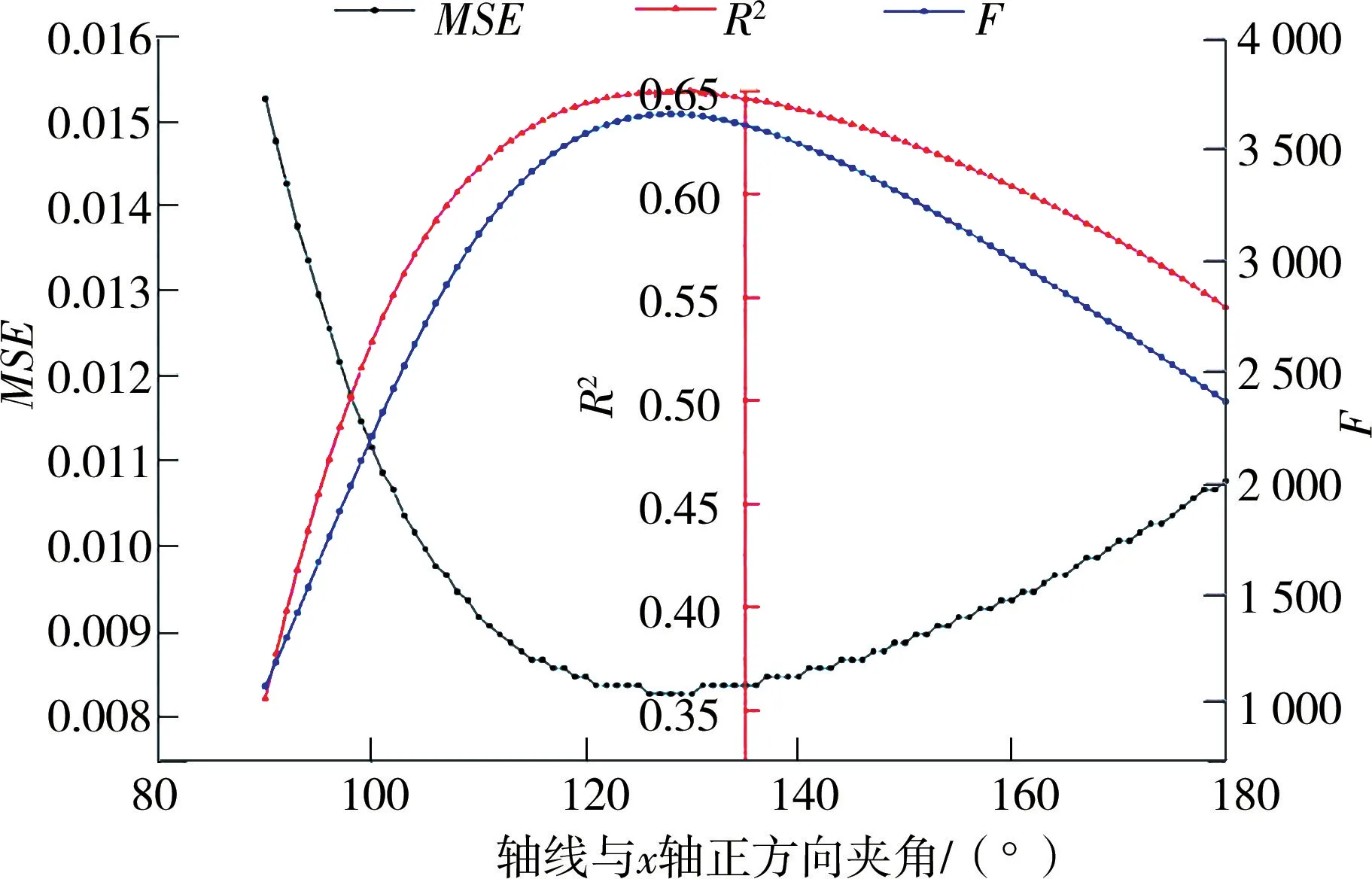
图5 NDVI与投影距离回归模型统计指标随轴线角度变化

为深入探究NDVI空间分布格局形成的原因，分析影响NDVI的气象因子（降水量和气温）与NDVI的相关关系。对样本点多年平均NDVI值分别与多年平均降水量和多年平均气温进行皮尔逊相关分析，得到降水量与NDVI的相关系数为0.72，气温与NDVI的相关系数为0.40。结果表明，降水量与NDVI有强相关性。鉴于此，用最佳地理轴线计算方法对NDVI主要影响因子降水量进行分析，以探析研究区内降水的空间分布格局是否具有同样的显著条带性分布规律。提取研究区内1 990个样本点的15 a平均降水量，将其与在不同轴线上的投影距离分别建立回归关系，R2、F统计值和回归模型的均方误差MSE随轴线角度变化规律如图6所示。对于降水量，每一条轴线对应的回归模型也均通过了0.05显著性水平F检验，说明降水也受地理因子影响。由图6可知，降水的最佳地理轴线角度为西偏北53°，此时回归模型F统计值最大，MSE最小，R2最大为0.791 4。

图6 降水量与投影距离回归模型统计指标随轴线角度变化

对比图5和图6可以看出，随着轴线角度在经线和纬线之间转移，NDVI与投影距离回归模型和降水与投影距离回归模型基本展现出了较为一致的变化规律，均能找到R2最大、F统计值最大、均方误差MSE最小的一个角度，且NDVI的最佳地理轴线为西偏北52°，降水的最佳地理轴线为西偏北53°，二者仅偏差1°。同时也可看出，在最佳地理轴线附近一定区域内的角度，其R2与最佳地理轴线对应的R2相差不大，为量化最佳地理轴线与其他角度上的R2差异，根据斜率计算公式做出R2变化斜率图（见图7），由图7可知，无论是降水量还是NDVI，最佳地理轴线附近的轴线R2变化平缓，距离最佳地理轴线远的轴线R2变化相对明显，角度偏向纬线方向的轴线比角度偏向经线方向的轴线R2变化平缓。若以斜率的绝对值0.001作为阈值，则可以确定一个最佳地理轴线范围，即对于NDVI，123°～137°是其具有显著条带变化的方向，对于降水量，123°～133°是其具有显著条带变化的方向。

图7 R2变化斜率随轴线角度变化

通过对黄河源区植被指数空间分布最佳地理轴线角度的计算，以及影响植被指数主要气象因子降水量的空间分布最佳地理轴线角度计算发现，研究区内NDVI的最佳地理轴线角度为西偏北52°，降水的最佳地理轴线角度为西偏北53°，且NDVI与降水量均在最佳地理轴线附近一定区域内，呈现出较为显著的条带性分布特征，二者的最佳地理轴线角度仅偏差1°，这也很好地解释了为何研究区内NDVI与降水量强相关。由此可见，在空间分布上，黄河源区降水量与NDVI的条带变化规律具有较高的一致性，但存在微小差异，这是因为植被分布同时还受气温、土壤等因素影响。综上所述，黄河源区的植被空间分布受地理因子影响，但地理因子只是影响植被分布的间接因子，造成黄河源区植被空间分布格局的机制主要是降水的分布规律。