NAM降雨径流模型的参数全局敏感性分析
2022-05-20赵然杭王兴菊顾士升
赵然杭,伍 谋,王兴菊,齐 真,周 璐,顾士升
(1.山东大学 土建与水利学院,山东 济南 250061;2.山东省防汛抗旱物资储备中心,山东 济南 250013)
NAM模型由丹麦学者Nielsen和Hansen于1973年首次提出[1],后经丹麦水力研究所逐步完善,是用于模拟流域范围内由降雨产生的径流过程的集总式概念性水文模型[2]。由于NAM模型结构简单、模型参数较少,因此在我国的流域降雨径流模拟中得到较为广泛的应用[3]。NAM模型不仅可以单独用于流域降雨径流模拟,也可以与MIKE11水动力模型耦合进行河道洪水过程模拟[4]。
模型概化使得模型与实际的物理过程差异较大,且NAM模型中很多参数难以通过实测方式获取,需要通过模型率定获得,导致参数值存在一定的不确定性,从而影响模拟预测结果[5-6]。参数敏感性分析是水文模型构建与应用的关键环节,其目的在于定性或定量评估模型参数对模拟结果的影响,确定参数的重要程度,从而识别敏感参数,以提高模型参数率定的效率,降低参数值的不确定性影响[7],避免出现异参同果现象[8]。参数敏感性分析方法可根据作用范围分为局部敏感性分析方法和全局敏感性分析方法,局部敏感性分析方法只分析单个参数对模型输出结果的影响程度,而全局敏感性分析方法检验多个参数及参数间相互作用对模型输出结果产生的影响[9]。常见的全局敏感性分析方法有偏相关法[10]、Sobol法[11]、FAST法[12]等。
近年来,国内外学者对水文模型的敏感性进行了相关研究。刘松等[13]联合运用Morris和Sobol法对三水源新安江模型进行了全局输出结果分析,研究了参数间的相关性对模型参数敏感性的影响;温娅惠等[14]基于单目标与多目标GLUE方法研究了新安江模型参数的不确定性和敏感性,表明多目标函数条件下的模型参数不确定性范围较大;于永强等[15]基于LH-OAT敏感性分析方法分析了MIKE11模型参数的全局敏感性,表明降雨强度、雨型和评价目标不同会影响模型参数的敏感性;Werkhoven等[16]对SAC-SMA模型参数进行全局敏感性分析,优先考虑敏感参数,降低了模型维数。Liu等[17]通过耦合Morris分析方法与NSDE算法对MIKE/NAM降雨径流模型进行参数敏感性分析与率定,筛选了模型敏感参数,提高了模型率定的效率;Zaghloul等[18]利用人工神经网络研究了SWMM模型参数的全局敏感性,并与重复试验结果进行对比分析。目前对NAM模型的参数敏感性分析较少且主要针对其中部分参数的局部敏感性,如李磊等[19]利用扰动分析法,分析了NAM模型中5个不同参数的局部敏感性;王振亚等[20]基于灰色系统关联度分析方法研究了NAM模型中地表蓄水层最大含水量、浅层蓄水层最大含水量、地表径流系数、壤中流系数、汇流时间常数对径流深、洪峰流量和峰现时间模拟结果的影响;解恒燕等[21]基于扰动分析法分析了NAM模型中9个主要参数的敏感性。以上研究表明,水文模型参数在高维空间通常会表现出较强的相关性[7],针对NAM模型部分参数的局部敏感性分析,忽略了模型参数之间的相互作用对模拟结果的影响,因此有必要利用全局敏感性分析方法对NAM模型参数进行敏感性分析。
笔者以小清河黄台桥断面以上321 km2为研究区域,采取拉丁超立方抽样方法随机抽取1 000组初始模型参数,利用互信息法和偏秩相关法对NAM模型参数进行全局敏感性分析,研究NAM模型参数对模拟结果中的洪峰流量、峰现时间、径流总量的影响,以进一步提高模型模拟精度和减少建模工作量。
1 模型与方法
1.1 NAM模型
NAM模型是一个用于模拟自然流域降雨径流过程的集总式概念性水文模型[22]。模型中影响流域水循环的土壤状态被描述为一系列简化的数学语言形式,并将流域产汇流分为融雪蓄水层、地表蓄水层、浅层蓄水层、地下蓄水层4个相互关联的蓄水层进行模拟计算,每一层代表流域内不同的物理元素。
NAM模型的参数及输入量是定义在整个流域上的,即为流域的平均值[23]。模型要求的输入数据有限,主要包括降雨量数据、蒸发量数据和模型参数。NAM模型的主要参数及其一般取值范围见表1。

表1 NAM模型主要参数及其取值范围
1.2 互信息法
互信息是指两个及两个以上变量之间共享的信息量[24],用于度量随机变量间的相互影响程度,即变量间的相关性大小,互信息越大,相关性越强。互信息法分析得出的R统计量可识别NAM模型参数与输出的径流总量、峰现时间、洪峰流量之间的非线性相关关系,用于NAM模型参数的全局敏感性分析。但R统计量只能识别参数敏感性的大小,无法识别NAM模型参数与输出的径流总量、峰现时间、洪峰流量之间的正负相关关系[25]。
两随机变量X与Y之间的互信息定义为
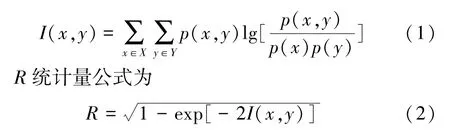
式中:p(x)为离散型随机变量X取值x的概率;p(y)为离散型随机变量Y取值y的概率;p(x,y)为X取值x、Y取值y同时发生的概率。
1.3 偏秩相关法
偏秩相关分析是一种非参数统计分析方法,在等级位差的基础上,通过控制其他因变量对输出结果的影响来分析两个变量之间的相关关系[26],可准确地反映自变量与因变量之间的线性关系,用于分析参数的全局敏感性。其P值(偏秩相关系数)的绝对值大小与计算值正负可分别识别参数敏感性的大小及输入参数与输出结果间线性关系的正负。
令输出结果为Y,输入参数为X1,X2,…,Xn,设这n+1个变量之间的Spearman秩相关系数r组成的矩阵为T,求矩阵T的逆矩阵得矩阵C。

第i个输入参数Xi与输出结果Y之间的偏秩相关系数PXi为
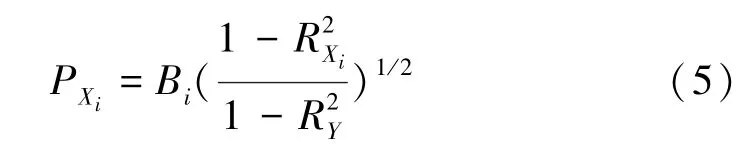
2 研究区域与模型构建
选取小清河黄台桥断面以上321 km2为研究区域,该研究区域位于山东省济南市,包括整个济南市主城区和南部山区及部分西北郊区,属温带季风气候区,降水主要集中于6—9月,多年平均降水量为671.1 mm。研究区域内设有黄台桥、东红庙、燕子山、刘家庄、吴家铺、绍而和兴隆7个雨量站。
通过对研究区域内7个雨量站2009—2013年的实测降雨资料及流量资料进行分析研究,选用20120708、20130709和20130723场次暴雨洪水过程进行参数率定,并以20110702、20120818和20130719场次暴雨为基准进行验证。根据率定期内3场暴雨洪水过程得出流域率定参数,见表2,模拟计算结果见表3和图1。
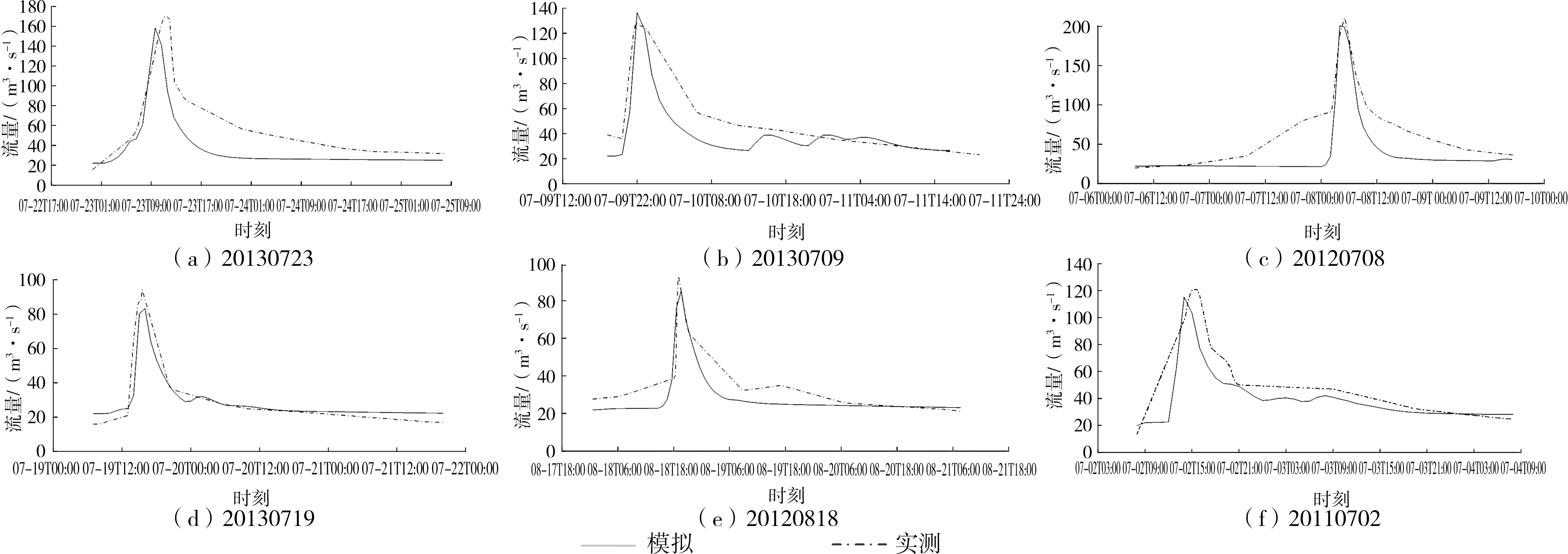
图1 率定期与验证期洪水过程模拟结果

表2 NAM模型模拟参数率定结果
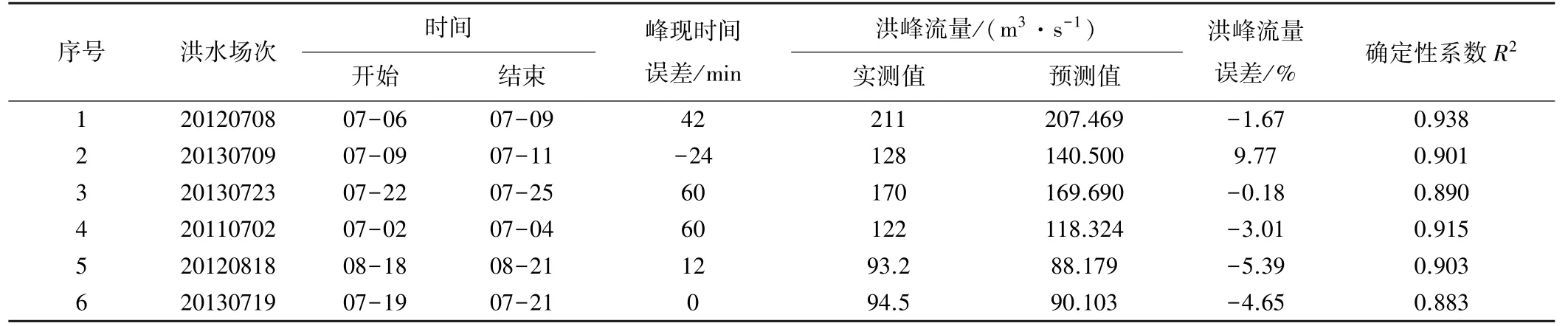
表3 各场次降雨洪水模拟结果
在3场率定洪水场次中,确定性系数R2分别为0.938、0.901和0.890,洪峰流量误差分别为-1.67%、9.77%和-0.18%,峰现时间误差分别为42、-24、60 min。在3场验证洪水场次中,确定性系数R2分别为0.915、0.903和0.883,洪峰流量误差分别为-3.01%、-5.39%、-4.65%,峰现时间误差分别为60、12、0 min。综上,本模型对率定期和验证期共6场次暴雨洪水模拟计算的确定性系数均大于0.85,洪峰流量相对误差均小于20%,峰现时间误差均小于180 min,根据《水文情报预报规范》可知,本模型的模拟精度达到良好水平,可以反映该流域流量的变化规律。说明NAM模型在研究区域内有较好的适用性,可用于模型参数的全局敏感性分析。
3 结果与分析
利用拉丁超立方抽样方法在9个参数值各自取值范围内随机抽取1 000组初始模型参数,通过MATLAB编写脚本写入NAM模型的输入文件中,将1 000个输入文件依次代入模型进行模拟计算得到相应的洪峰流量、峰现时间和径流总量,再将参数值、模拟结果组成3个10×1 000的矩阵,利用互信息法和偏秩相关法对NAM模型进行全局敏感性分析,敏感次序排第一和第二的参数即为敏感参数。
3.1 互信息分析
互信息分析方法得到的各参数对洪峰流量、峰现时间和径流总量的敏感性分析结果见表4。

表4 互信息分析结果
根据表4中的R统计值可以判断参数和输出结果之间非线性关系的强弱,即参数敏感性的大小。
对于洪峰流量,9个参数的R统计值处于0.162~0.379之间,说明各参数与洪峰流量的非线性关系较弱。其中,参数CK12的R统计值最大,为0.379,说明与其他参数相比,CK12的参数敏感性较强。对于峰现时间,C K12的R统计值最大,为0.683,说明CK12为最敏感参数,与峰现时间的非线性关系强于其他参数;第二敏感参数是TOF,R统计值为0.310。对于径流总量,敏感参数分别为TOF和CK12,R统计值分别为0.434和0.426。
3.2 偏秩相关分析
偏秩相关法得到的洪峰流量、峰现时间和径流总量对各参数的敏感性分析结果见表5。

表5 偏秩相关分析结果
由表5中P值的绝对值大小可以得出参数和输出结果之间线性相关关系的强弱,即参数的敏感性大小。P值正负可以反映参数和输出结果之间线性相关关系是呈正相关还是负相关。
对于洪峰流量,最敏感的参数是TOF,P值为-0.598;第二敏感参数是CK12,P值为-0.418,说明参数TOF和C K12与洪峰流量的线性相关关系强于其他参数,均为负相关关系。
对于峰现时间,参数CK12的P值最大,为0.817,说明CK12为最敏感参数,与峰现时间的线性相关关系强于其他参数,呈正相关,在率定过程中可优先率定参数C K12。
对于径流总量,最敏感的参数是TOF,P值为-0.594;第二敏感参数是CK12,P值为-0.434,说明TOF和CK12与径流总量的线性关系强于其他参数,均为负相关关系。
3.3 结果对比分析
将偏秩相关分析的结果和互信息分析的结果进行对比发现,对于洪峰流量,两种方法求得的敏感参数都为TOF和CK12。在互信息分析结果中,参数CK12的R统计值为0.379,TOF的R统计值为0.282,说明参数CK12的敏感性强于TOF;在偏秩相关分析结果中,参数CK12的P值为-0.418,TOF的P值为-0.598,说明参数CK12的敏感性弱于TOF。
对于峰现时间,两种方法求得的最敏感参数都是CK12,互信息法求得的R统计值为0.683,偏秩相关法求得的P值为0.817,说明C K12与峰现时间的线性关系更为显著。
对于径流总量,两种方法求得的最敏感参数都是TOF,互信息法求得的R统计值为0.434,偏秩相关法求得的P值为-0.594,说明TOF与径流总量的线性关系更为显著。
3.4 讨 论
对于洪峰流量,两种方法求得的敏感参数均为CK12和TOF,但两个参数的敏感次序不同,考虑到互信息法和偏秩相关法分别基于非线性和线性来识别敏感性参数,因此参数的敏感次序排列有所不同是不可避免的。对比其他学者对NAM模型参数敏感性分析结果,李磊等[19]的研究结果表明参数CK12对洪峰流量影响较大,与本文的结论一致。
对于峰现时间和径流总量,互信息法和偏秩相关法求得的最敏感参数结果一致,峰现时间的最敏感参数均为CK12,R值为0.683,P值为0.817,说明与峰现时间的线性关系较为显著,呈正相关;径流总量的最敏感参数均为TOF,R值为0.434,P值为-0.594,说明与径流总量的线性关系较为显著,呈负相关。两种方法的共同使用,避免了只使用单一方法的局限性,可全面地识别敏感参数。
对比其他学者对NAM模型参数敏感性分析结果,王振亚等[20]的研究表明参数CK12与峰现时间的关联度最大,C QOF次之,本文中CQOF的敏感次序为3,其原因为前者未考虑参数TOF对峰现时间的影响;解恒燕等[21]的研究表明参数Lmax和Umax对径流总量的影响较为明显,但其研究区域Fisher小流域地势较为平坦且多为自然地貌,而本文研究区域小清河黄台桥断面以上321 km2流域,地势南高北低且多为城市地形,说明在不同下垫面情况的流域,对径流总量影响最大的参数不同。
4 结 论
针对NAM模型参数,利用拉丁超立方抽样方法抽取模型输入样本,使用互信息法和偏秩相关法进行NAM模型参数全局敏感性分析,得到以下结论。
(1)通过拉丁超立方抽样方法抽取了1 000组模型输入样本,保证了NAM模型参数值数据的代表性和均匀性。互信息法通过分析参数与模拟结果间的非线性关系识别敏感参数,偏秩相关法通过分析参数与模拟结果间的线性关系识别敏感参数,且两者均为全局敏感性分析方法,两种方法共同使用可避免只使用单一方法存在的局限性,全面准确地识别敏感参数,保证结论的合理性及可靠性。
(2)在两种不同敏感性分析方法结果中,参数TG、TIF、CKIF、Umax和Lmax的R统计值和P值均较小,说明这些参数为不敏感参数,在模型率定时可以根据经验取固定值以提高率定效率。TOF和CK12是对洪峰流量敏感性最大的参数,且与洪峰流量呈负相关;CK12是对峰现时间敏感性最大的参数,随着CK12增大,峰现时间会相应延长;TOF是对径流总量最为敏感的参数,呈负相关,随着TOF增大,径流总量会相应减小。
(3)通过全局敏感性分析,识别了NAM模型的敏感参数,为后续模型率定及耦合提供参考和指导,减少建模的工作量,提高模型率定的效率。
