磁流变阻尼器悬架系统非线性振动行为分析

韩刚,刘瑞,吕鹤

(齐齐哈尔大学 机电工程学院,黑龙江齐齐哈尔 161006)

悬架系统是车辆重要组成部分,影响车辆的行驶平顺性和操纵稳定性。国内外学者分别采用理论研究方法和实验研究方法,对悬架系统振动问题进行了大量的研究工作。张俊红等[1]以半车四自由度悬架振动系统为研究对象,分析了悬架弹簧非线性刚度、减振器非线性阻尼对汽车平顺性的影响。侯彦羽[2]对汽车悬架系统进行了数值仿真研究,发现了周期运动、倍周期分岔等复杂动力学行为,得出了选择适当的系统参数组合,可以避免系统在运行过程中出现混沌现象并能改善系统运行品质的结论。王增才等[3]在SimMechanics下建立七自由度车辆模型并进行了仿真,验证了半主动空气悬架能够有效提高车辆倾翻阈值,改善车辆抗侧翻的能力。李徐东[4]运用平均法对汽车悬架系统的非线性振动微分方程求解并分析了振动特性,揭示了汽车悬架的非线性振动机理。常一帆[5]建立路面随机激励作用下汽车悬架系统单自由度模型,使用同伦分析法研究汽车非线性振动特性并证明了该方法的有效性。Chen等[6]通过四分之一车辆模型利用李雅普诺夫指数来识别混沌运动的起始点,并采用状态反馈控制来防止混沌运动,研究了非线性悬架系统的动力学控制问题。陈晓建等[7]以2-DOF非线性悬架动力学模型为例,利用增量谐波平衡法分析了在不同激励比和非线性刚度系数作用下对振动系统各谐波响应的影响,得出了多种非线性特性。Jayachandran等[8]通过优化被动悬架系统的刚度和阻尼系数来提高乘用车的平顺性,引入了一种采用“空钩”控制方法的半主动控制系统。成洁[9]建立了四分之一车辆悬架系统非线性模型,分析了非线性弹簧恢复力对悬架振动时域响应的影响。宋作军[10]进行了双质量块形式的悬架模型稳定性分析,得到了簧载质量和非簧载质量的时域响应及相图,为半主动悬架系统的设计及控制提供了数据支持。

采用SolidWorks与SimMechanics联合仿真分析方法,综合分析整车悬架系统的几何和阻尼非线性因素对车身振动行为的影响规律,为汽车悬架系统的优化设计提供理论参考。

1 简化的整车振动系统SolidWorks三维实体建模

SimMechanics动力学软件包具有强大的动力学仿真功能,但是仿真模型建立过程中几何位置和惯性参数获取困难。SolidWorks建立三维实体模型具有直观性和高效性的优点,并且SolidWorks与SimMechanics所建立的模型间有着良好的接口转化能力,因此联合二者进行仿真模型搭建可以自动转化几何位置和惯性参数,提高建模的速度和准确性。

汽车的振动行为十分复杂,本文只分析对整车安全和乘坐舒适性影响较大的铅垂方向的车身非线性振动行为。因此,为了提高仿真分析效率,忽略了对整车该方向振动行为影响甚小的悬架附属结构,如简化汽车底盘,忽略转向系统、传动系统、控制系统,忽略各运动副内的摩擦力等。振动源只考虑路面的简谐激励,使问题的研究既简便又不失一般性[11-12]。表1是通过查阅相关资料获得的建模所需要的几何和动力学特性参数。

表1 几何与动力学特性参数

依据以上主要参数,使用SolidWorks软件对试验台、车轮、悬架系统(前悬架为麦弗逊独立悬架,后悬架为多连杆独立悬架)和车身4个子系统分别进行三维模型的建立,然后根据各部分的连接关系装配成整车模型,如图1所示。

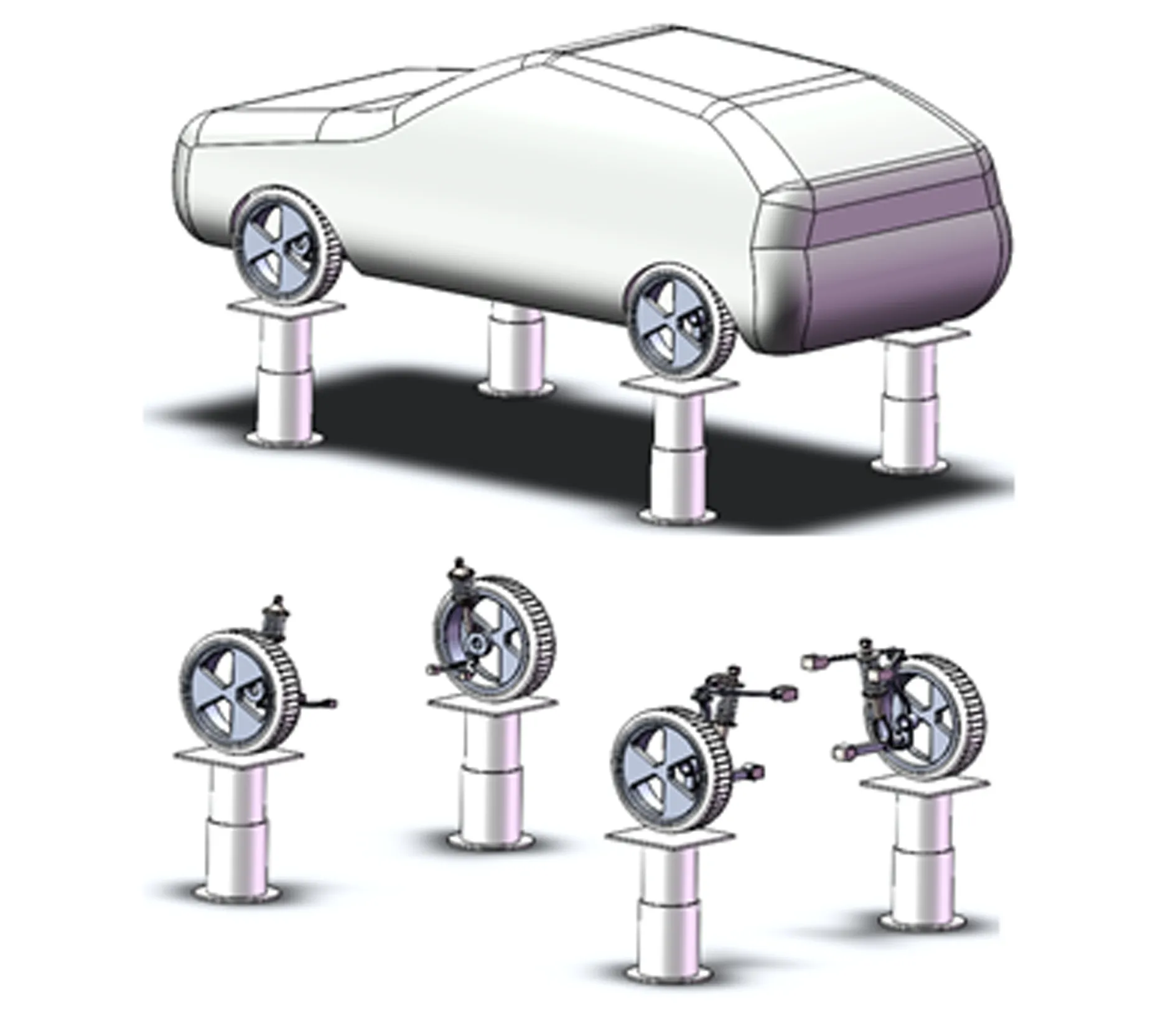
图1 前麦弗逊与后多连杆悬架模型

2 SolidWorks实体模型向SimMechanics仿真模型的转化

SolidWorks三维实体模型转化为SimMechanics动力学仿真模型的具体过程如图2所示。首先,将SolidWorks建立的车辆零部件实体模型进行装配,生成整车装配模型。其次,在SolidWorks装配环境通过软件数据转换技术,将装配体转变成XML文件(此文件存储着装配体的详细模型描述数据)和STEP/STL文件(此文件包含了装配体零件的几何性质)。最后,将导出的XML文件和STEP/STL文件导入SimMechanics转化形成SLX文件和一个数据文件。

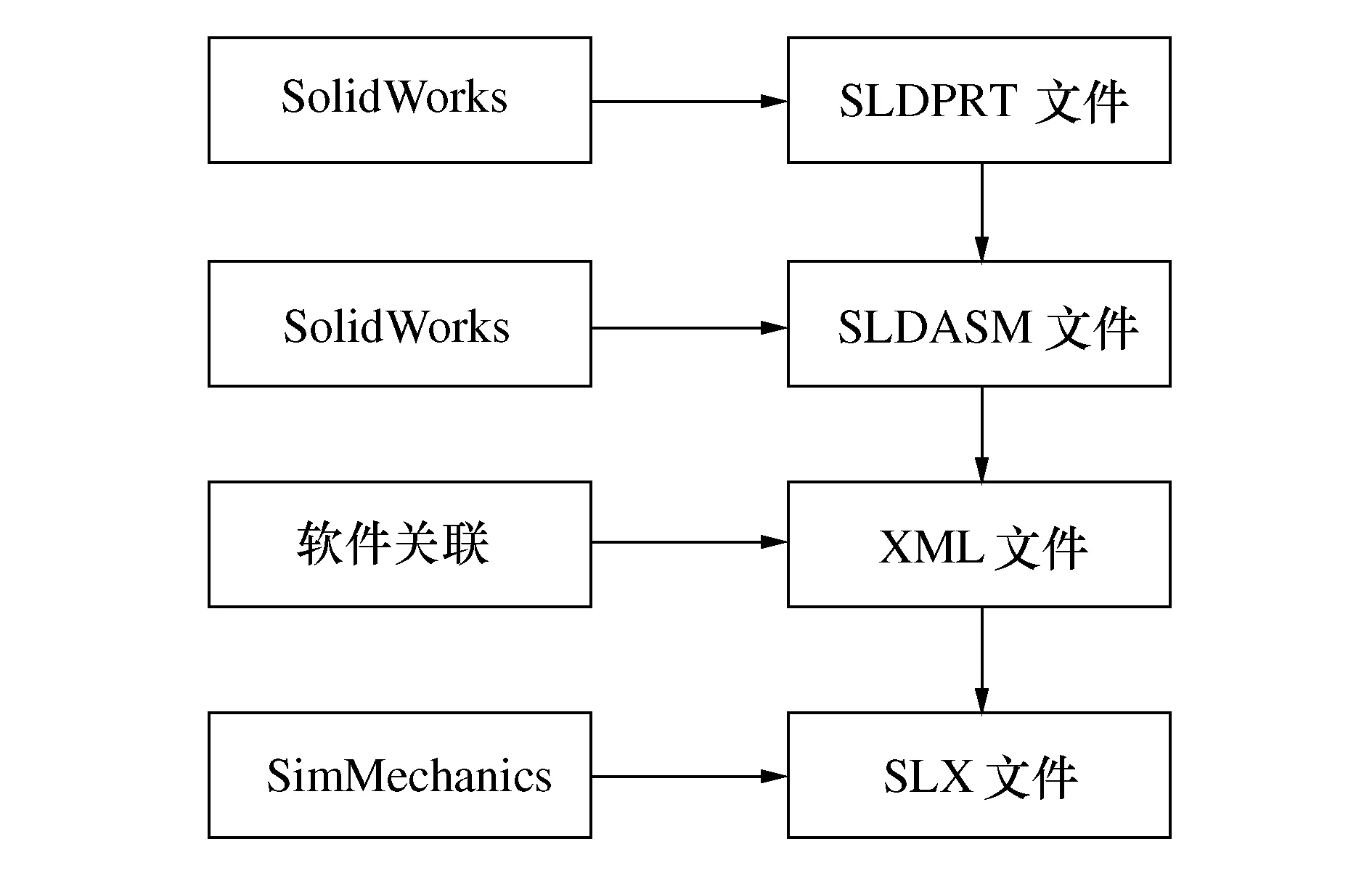
图2 SolidWorks实体模型向SimMechanics仿真模型的转化过程

图3是转化并完善后得到的SimMechanics机械动力学仿真模型。图中系统Input是外激励输入模块,Configuration是环境配置模块,CL-XX是车轮模块,dlg是多连杆悬架模块,mfx是麦弗逊悬架模块,CS是车身模块。

图3 SimMechanics动力学仿真模型

3 几何非线性对车身振动行为影响的仿真分析

汽车实际悬架系统是一个复杂的空间杆机构系统,各构件间具有复杂的运动和联接关系。悬架系统在运动过程中,由于悬架的几何角度变化范围大,所以悬架的弹性恢复力和阻尼力的大小与车身的运动位移和速度变化的函数关系呈现几何非线性特性。在上述SimMechanics动力学仿真模型的基础上,通过振动台给四轮施加相同的正弦谐波外激励。外激励幅值设定为0.02 m,通过频率由小到大的逐渐变化,观察车身垂直方向位移响应的变化情况,仿真结果如图4所示。

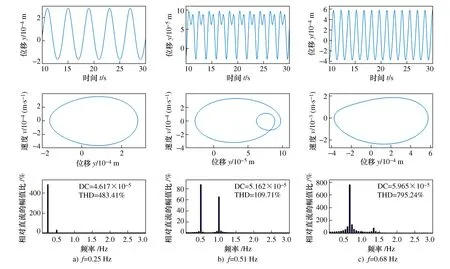
图4 外激励A=0.02 m时车身位移-时间历程曲线、相平面图和频谱图

由图4频谱图可知,振动响应主要是由一次谐波和二次谐波成分组成,并且一次谐波为主要成分。外激励频率在小于0.51 Hz范围内变化时,随着外激励频率的增加,二次谐波成分相比一次谐波成分逐渐增大。外激励频率达到0.51 Hz时,二次谐波成分占比达到最大。当外激励频率在0.51～1 Hz范围内变化时,二次谐波成分占比逐渐减小,而一次谐波成分占比逐渐增大。

由图4车身位移-时间历程曲线和相平面图可知,外激励频率小于0.51 Hz范围时,非线性特性随外激励频率的增加逐渐增强。而当外激励频率在大于0.51 Hz范围内变化时,非线性特性随外激励频率的增加又逐渐减弱。

图5是外激励频率为0.51 Hz,幅值从小到大逐渐变化时,车身的垂直位移-时间历程曲线、相平面图和频谱图。

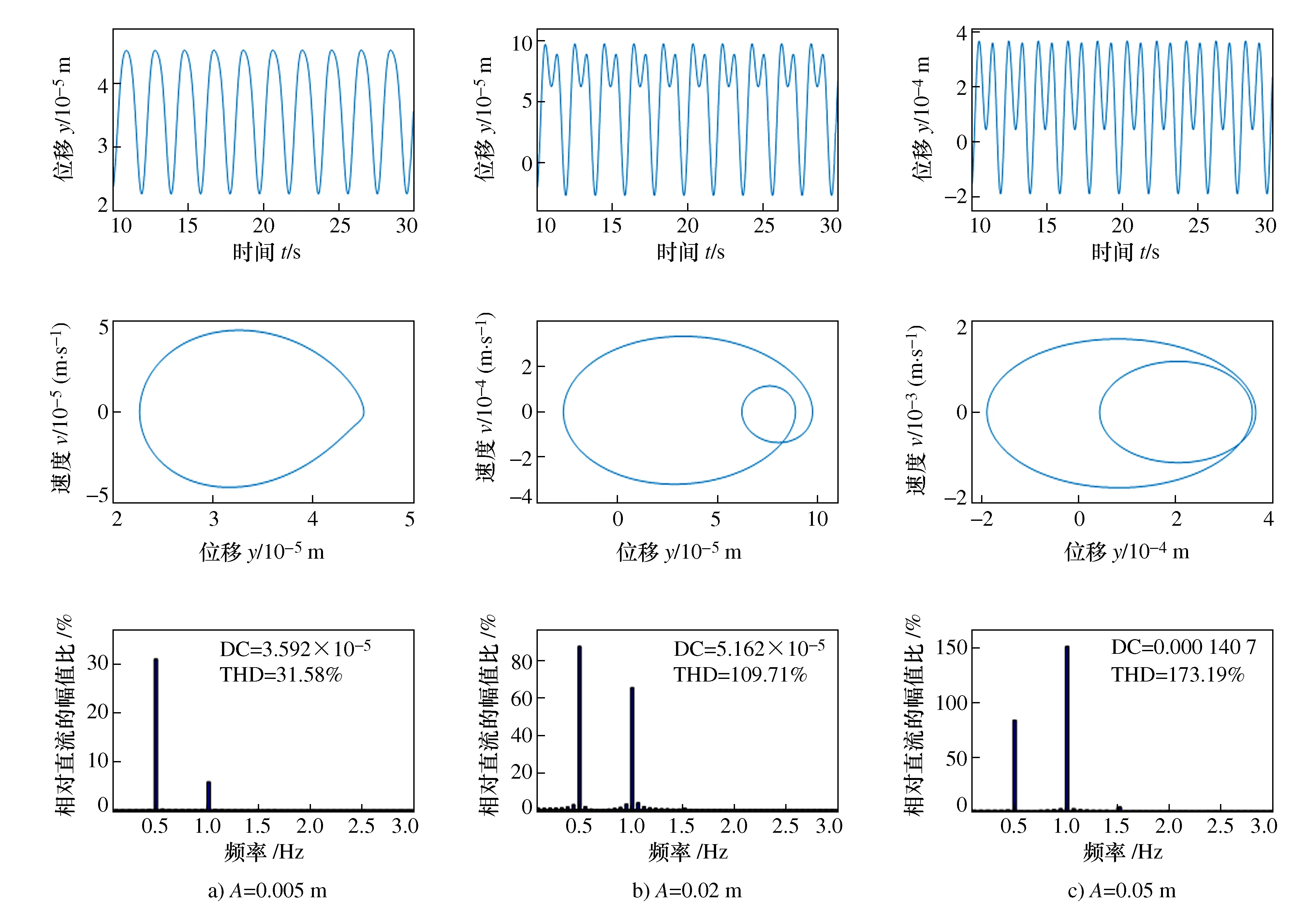
图5 外激励f=0.51 Hz时车身位移-时间历程曲线、相平面图和频谱图

从图5频谱图中可以看出,随外激励幅值的增加,二次谐波成分在整个响应中占比逐渐增大。幅值达到0.05 m时,二次谐波成分占比超过一次谐波成分,成为整个响应中的主要谐波成分。由图6给出的瞬时响应的车身位移的频谱图可知,车身对应一阶模态频率为1 Hz。此时,外激励频率0.51 Hz约为一阶模态频率1 Hz的1/2倍。由此判断,系统发生了二次超谐波共振,出现二次谐波成分远大于一次谐波成分的现象。同时,由车身位移-时间历程曲线和相平面图可知,随着外激励幅值的增大,车身非线性特性也逐渐增强。

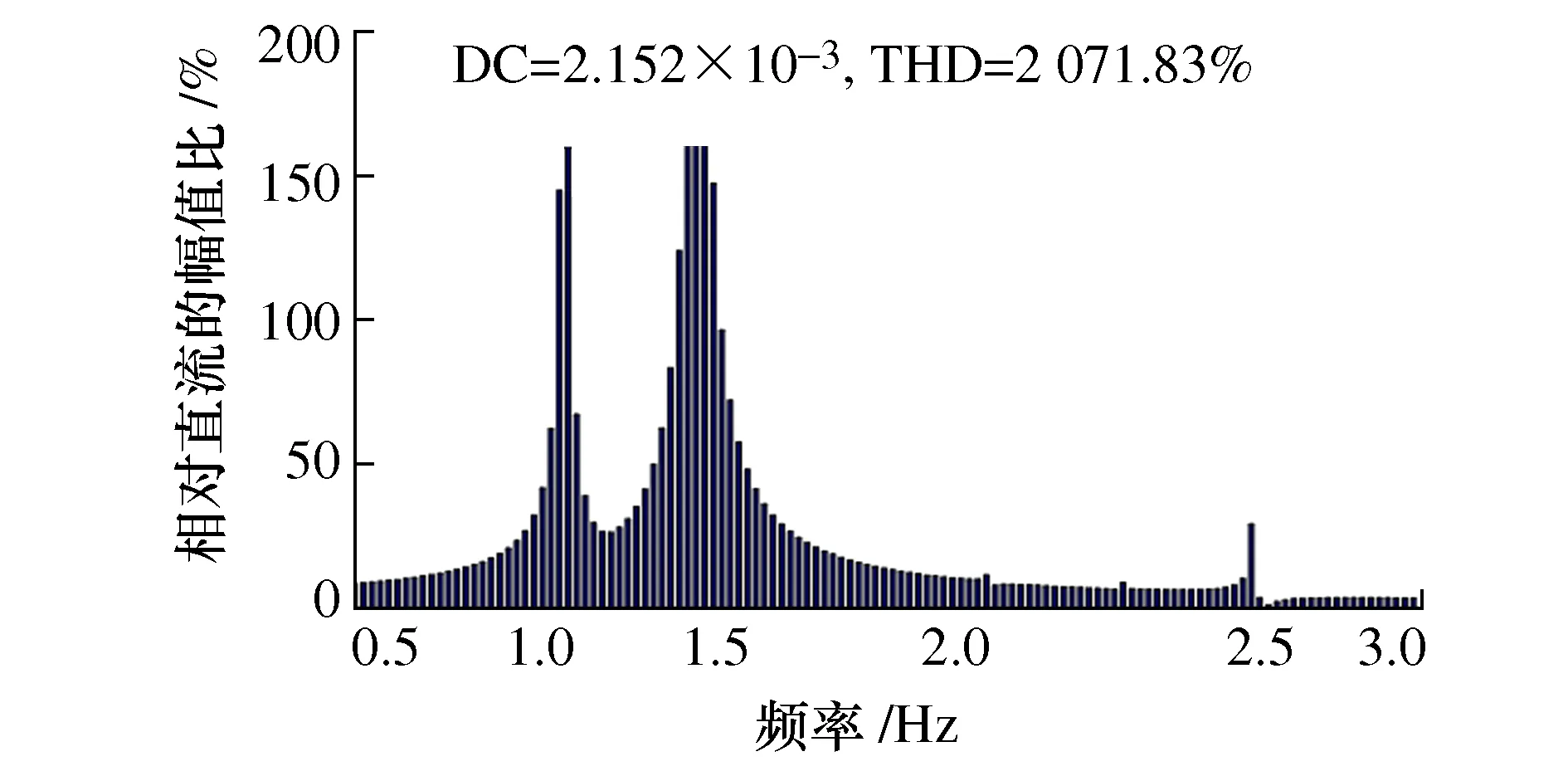
图6 车身频谱图

综合所述,在不同外激励频率和幅值情况下,由几何非线性悬架系统的仿真结果可以看出悬架系统的几何非线性特性在外激励频率为0.51 Hz附近尤为明显,当频率逐渐大于或者小于0.51 Hz时非线性特性逐渐减弱。而外激励频率不变时,外激励幅值的增大也会使非线性特性增强,当外激励幅值达到某一特定值,而外激励频率约为系统模态频率的1/2倍时,系统振动响应以二次谐波响应为主,出现二次超谐波共振现象。

4 磁流变阻尼对车身振动行为影响的仿真分析

磁流变阻尼器属于电磁式减振器中的一种。近几年来,由于其具备响应快、结构简单、可控性强和耗能低的特点,被广泛应用在各种主流悬架形式中[13-14]。本文研究的磁流变阻尼器是沙凌锋等[15]利用Sigmoid函数建立的磁流变阻尼器力学模型。这种磁流变阻尼器Sigmoid模型具有表达简单、拟合的力-位移关系和力-速度关系相对准确的优点,非常适合于磁流变阻尼器的工程设计和应用。本文采用的磁流变阻尼力模型为

(1)

式中:Fm为磁流变阻尼器最大屈服力;β为磁流变阻尼器的非线性系数。

基于上述的磁流变阻尼力模型,使用Simulink建立其仿真模型,如图7所示。图8给出其仿真输出的磁流变阻尼力随速度变化曲线。在上述磁流变阻尼器仿真模型基础上,在外激励频率f=0.2 Hz、幅值A=0.05 m、最大屈服力Fm=200 N,磁流变阻尼器非线性系数β逐渐增大情况下进行仿真,仿真结果如图9所示。

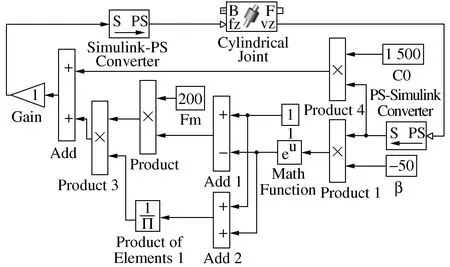
图7 磁流变阻尼器仿真模型

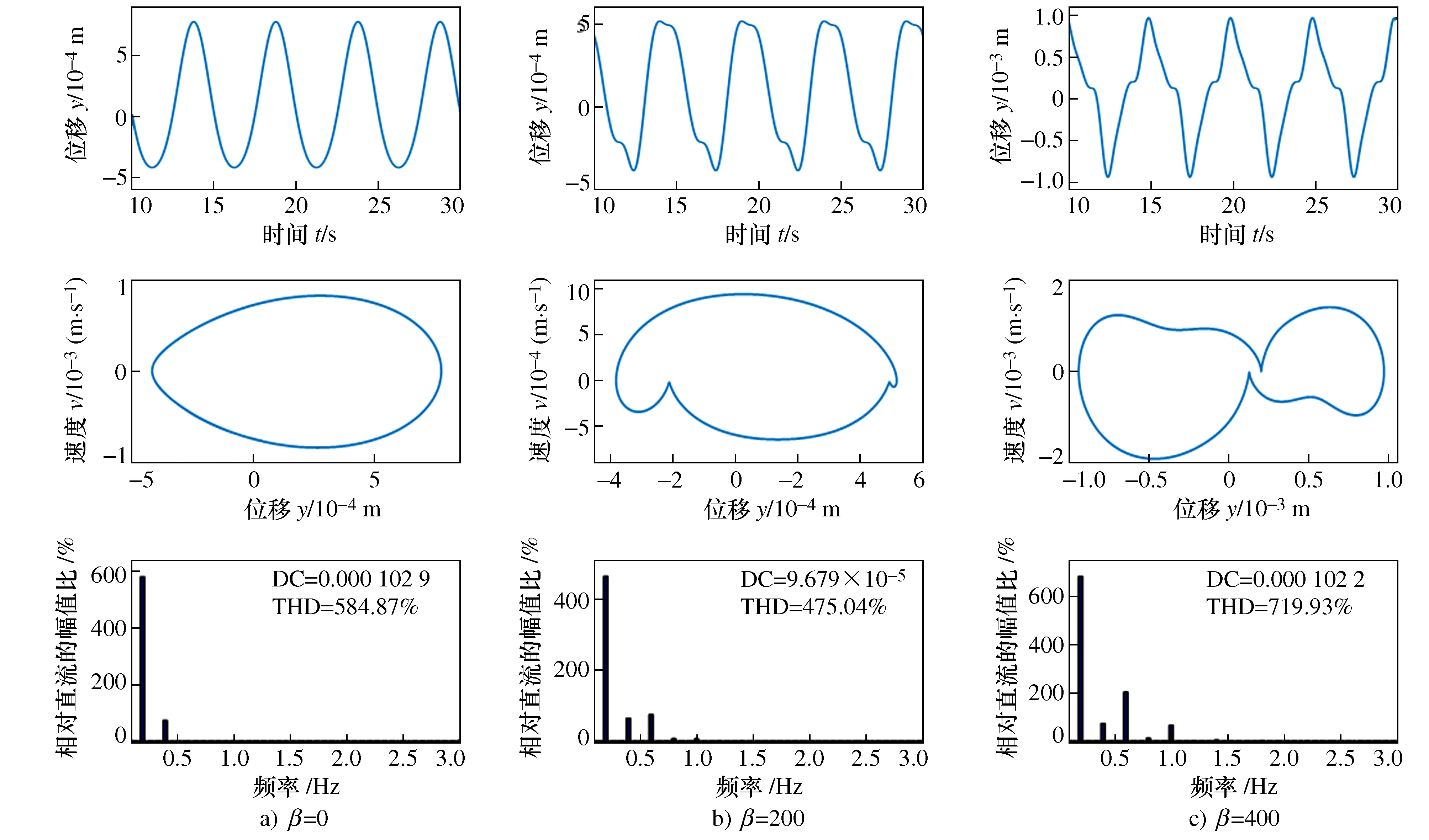
图9 外激励f=0.2 Hz、A=0.05 m、Fm=200 N时车身位移-时间历程曲线、相平面图和频谱图

由图9频谱图可以看出,系统无磁流变阻尼器(β=0)的时,系统响应中出现由几何非线性导致的二次超谐波成分。随着β的增大,磁流变阻尼力的引入,系统出现三次及以上的奇数次谐波成份,同时相邻的奇数次谐波幅值大于偶数次谐波幅值,但无论奇数次还是偶数次谐波幅值都随阶次的增加呈现逐渐递减的变化趋势。随着β的增大,系统响应中奇数次谐波成分占比也逐渐加大。

由图9位移-时间历程曲线和相平面图可知,随着β值的增大系统的非线性特性越来越明显。在外激励频率f=0.2 Hz、外激励幅值A=0.05 m以及β=200,最大屈服力Fm由小变大时,研究最大屈服力Fm变化对车身振动行为的影响,仿真结果如图10所示。

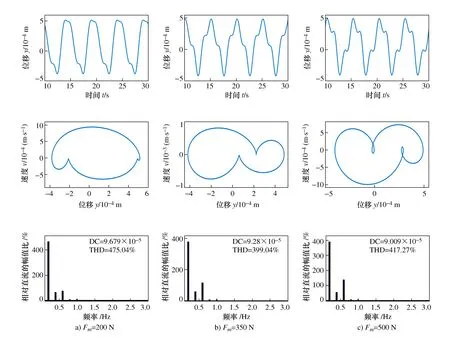
图10 外激励f=0.2 Hz、A=0.05 m、β=200时车身位移-时间历程曲线、相平面图和频谱图

由图10频谱图分析可知,随着Fm增加,系统奇数次谐波成分也逐渐增大。同时相邻的奇数次谐波幅值总是大于偶数次谐波幅值,但无论奇数次还是偶数次谐波幅值都呈逐渐递减的变化趋势。由图10车身位移-时间历程曲线和相平面图可知,随着最大屈服力Fm的增大,系统振动响应逐渐表现出更为复杂的非线性行为。

磁流变阻尼器的引入使系统响应出现三次及以上奇数次超谐波成分。这种非线性响应当外激励频率接近系统模态频率的1/3倍时,系统发生三次超谐波共振的趋势明显增加。由图11可知,当非线性系数β=300,最大屈服力Fm=400 N,外激励幅值A=0.05 m情况下,当外激励频率f=0.33 Hz和f=0.43 Hz的三倍值分别接近系统1阶(约1 Hz)和2阶(约1.3 Hz)模态频率时,由图11频谱图可知三次谐波幅值远远大于其它高次谐波幅值,出现明显的三次超谐波共振趋势,同时由图11车身位移-时间历程曲线和相平面图可以看到,系统响应的非线性特征也非常明显。由于算例中的阻尼值较大,系统三次谐波幅值并没有超过一次谐波幅值而发生共振,但是这种三次超谐波共振趋势是不容忽视的。

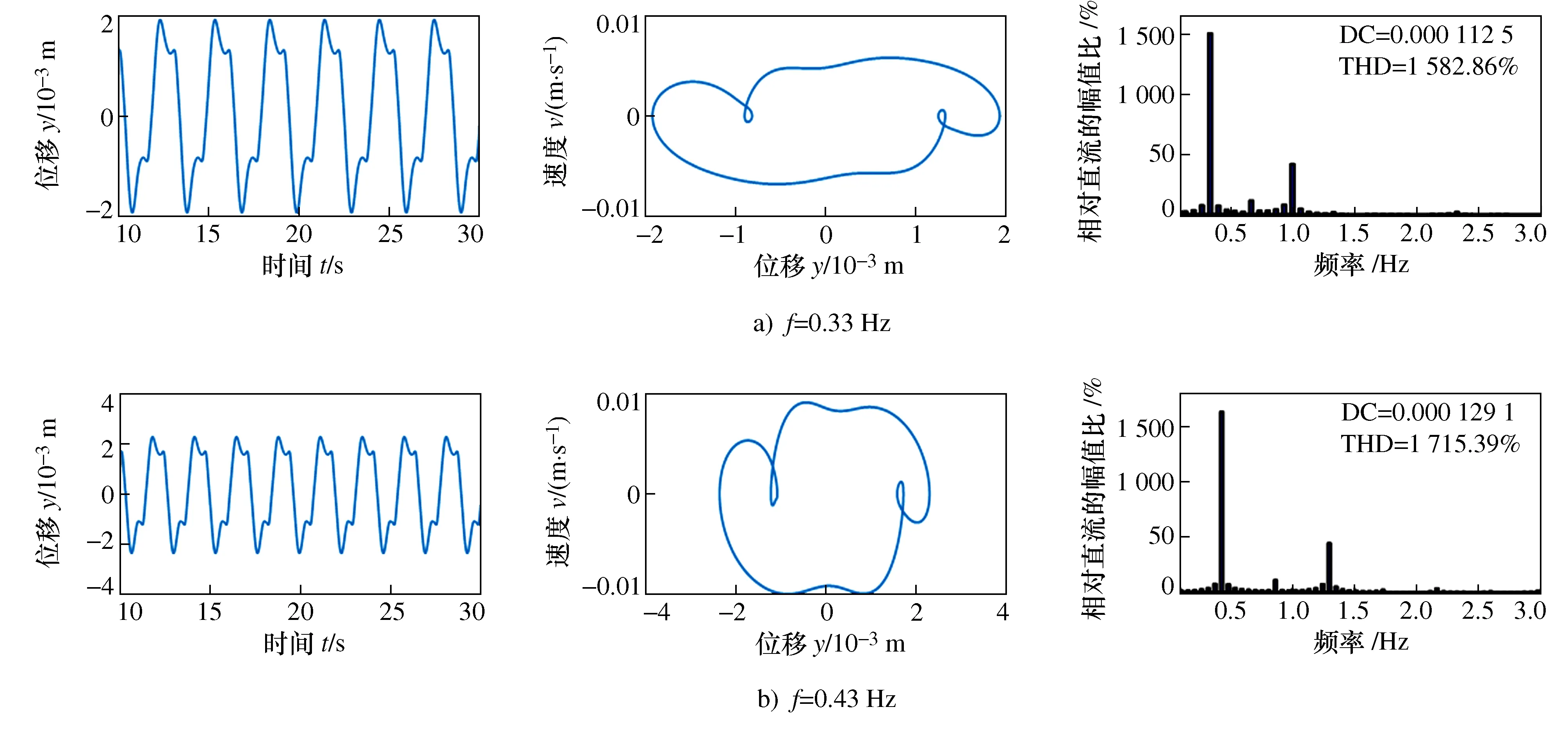
图11 外激励A=0.05 m、β=300、Fm=400 N时车身位移-时间历程曲线、相平面图和频谱图

图12和图13分别为不同磁流变阻尼器的非线性系数β和最大屈服力Fm值的幅频特性曲线。

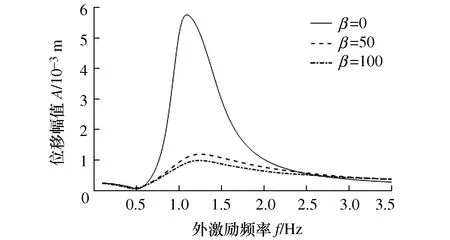
图12 不同β值时车身垂直位移响应幅频曲线

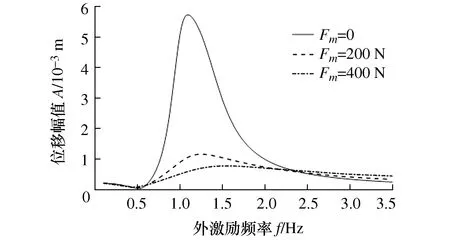
图13 不同Fm值时车身垂直位移响应幅频曲线

由图12可以看出使用磁流变阻尼器(β=50、β=100)相对于没有使用磁流变阻尼器(β=0)的车辆,在主共振区振动响应相差较为悬殊。使用磁流变阻尼器的车辆,在主共振区对车辆振动抑制效果较好。在主共振区,随着磁流变阻尼器非线性系数β的增加,对车身振幅的抑制效果明显,幅值大幅减小。在非主共振区,车身振幅随着非线性系数β的增加而小幅增大,但对车身振幅的影响较小。由图13可知,在共振区没有使用磁流变阻尼器(Fm=0)的车辆振动幅值最大,而使用磁流变阻尼器(Fm=200 N、Fm=400 N)的车辆振动幅值较小,且随着Fm的增加振动幅值也随之减小,但其主共振频率在增大。在共振区以外,振动幅值随着Fm的变小其也逐渐减小,但变幅不大。

5 结论

对实际车辆结构进行了适当简化,建立车身和整体悬架组成的振动系统模型,采用SolidWorks与SimMechanics联合仿真分析,研究悬架系统的几何非线性与非线性磁流变阻尼力对车身振动响应的影响,得到以下结论:

1) 使用磁流变阻尼器的整车悬架系统,其振动响应会受到几何非线性和非线性磁流变阻尼力的显著影响,表现出复杂的非线性振动行为。悬架系统几何非线性会使系统响应出现二次超谐波成分,而非线性磁流变阻尼力的引入又使系统出现了三次及以上奇数次谐波成分。

2) 特定的外激励频率和幅值情况下,系统会产生二次超谐波和三次超谐波共振。高次超谐波共振受现实阻尼力和激励幅值的制约,一般不会出现。

3) 磁流变阻尼器对共振区系统响应幅值有显著的抑制作用,可以大幅降低系统响应幅值,增大车辆行驶稳定性和安全性,这是采用磁流变阻尼器的主要原因之一。在非共振区,磁流变阻尼器对系统响应幅值影响不明显。但是由于磁流变阻尼器的存在,系统响应会出现三次及以上高次谐波成分,振动的非线性特征非常明显,导致车辆行驶过程中乘坐舒适性不佳。