变厚度复合材料加筋壁板剪切屈曲及后屈曲承载能力研究
2022-05-20高伟成炜赵常飞
高伟,成炜,赵常飞
(航空工业第一飞机设计研究院,西安 710089)
复合材料加筋壁板是机体主承力结构典型构件之一,其承受面内剪切载荷时,常见失效模式是剪切屈曲失稳[1-2]。加筋壁板剪切屈曲后,其后屈曲承载路径具有几何非线性的特点,工程师们一般以极限载荷下不得屈曲作为设计准则。加筋壁板屈曲后并不等于破坏,为有效降低其结构重量,充分发挥复合材料可设计性的优点,有必要对加筋壁板剪切屈曲及后屈曲承载能力进行研究。
国内外学者对复合材料加筋壁板剪切屈曲及后屈曲进行了大量研究。Mallela等[3]采用特征值法研究了加筋壁板的线性剪切屈曲响应特性;Ambur等[4]采用渐进损伤分析方法对加筋壁板剪切后屈曲承载能力进行模拟,并与试验结果进行验证;王新年等[5]采用P型有限元法研究了长桁横截面积对加筋壁板线性剪切屈曲的影响;张国凡等[6]基于渐进损伤剪切破坏模型,研究了加筋壁板失效模式和失效载荷;石经纬等[7]通过弧长法研究了不同铺层对加筋壁板剪切屈曲及后屈曲承载能力的影响;冯宇等[8]和汪厚冰等[9]采用工程算法和特征值法对T型加筋壁板剪切屈曲进行研究,并进行了试验验证;谭翔飞等[10]和王平安等[11]通过对角拉伸剪切试验,研究了加筋壁板在剪切载荷状态下的屈曲载荷、屈曲模态及后屈曲承载特性。工程上现有文献主要针对等厚度加筋壁板蒙皮剪切屈曲及其后屈曲承载能力研究,加筋壁板蒙皮一般为变厚度结构,使得现有文献研究成果的适用范围具有一定的局限性。针对此问题,在借鉴已有研究的基础上,开展了变厚度加筋壁板蒙皮剪切屈曲及其后屈曲承载能力研究。参考产品设计方案,选取加筋壁板蒙皮基本厚度、加厚区域厚度和铺层信息为基本参数,长桁横截面积几何信息为变量,采用特征值法和渐进损伤失效分析方法研究长桁横截面积对变厚度加筋壁板蒙皮剪切屈曲及后屈曲承载能力的影响,并开展该结构在剪切载荷作用下的屈曲及后屈曲承载能力试验研究,将试验结果与计算结果进行对比、分析特征值法和渐进损伤失效分析方法的准确性和实用性,及长桁横截面积对变厚度加筋壁板屈曲及后屈曲承载能力的影响,研究成果可为复合材料加筋壁板设计提供技术参考。
1 试验件设计
复合材料加筋壁板试验件由蒙皮和四根T型长桁通过共胶接工艺粘接成整体,且四边布置有与夹具剪切板连接的加强片。试验件设计有构型I和构型II两种构型加筋壁板,构型I和构型II加筋壁板试验件蒙皮基本区域厚度、加厚区域厚度和铺层角度信息相同;长桁几何参数信息不同。试验件加筋壁板蒙皮基本区域厚度1.84 mm,与长桁粘接处局部加厚到2.94 mm;构型I长桁缘条和腹板厚度均为2.21 mm,构型II长桁缘条和腹板厚度均为2.576 mm。试验件外形按平面考虑,长度参数选取600 mm,宽度选取520 mm。加筋壁板材料选用M21/34%/UD194高温固化环氧碳纤维单向带预浸料。材料性能见表1,铺层信息见表2,试验件几何尺寸见图1。

表1 复合材料性能参数

表2 加筋壁板基本铺层信息
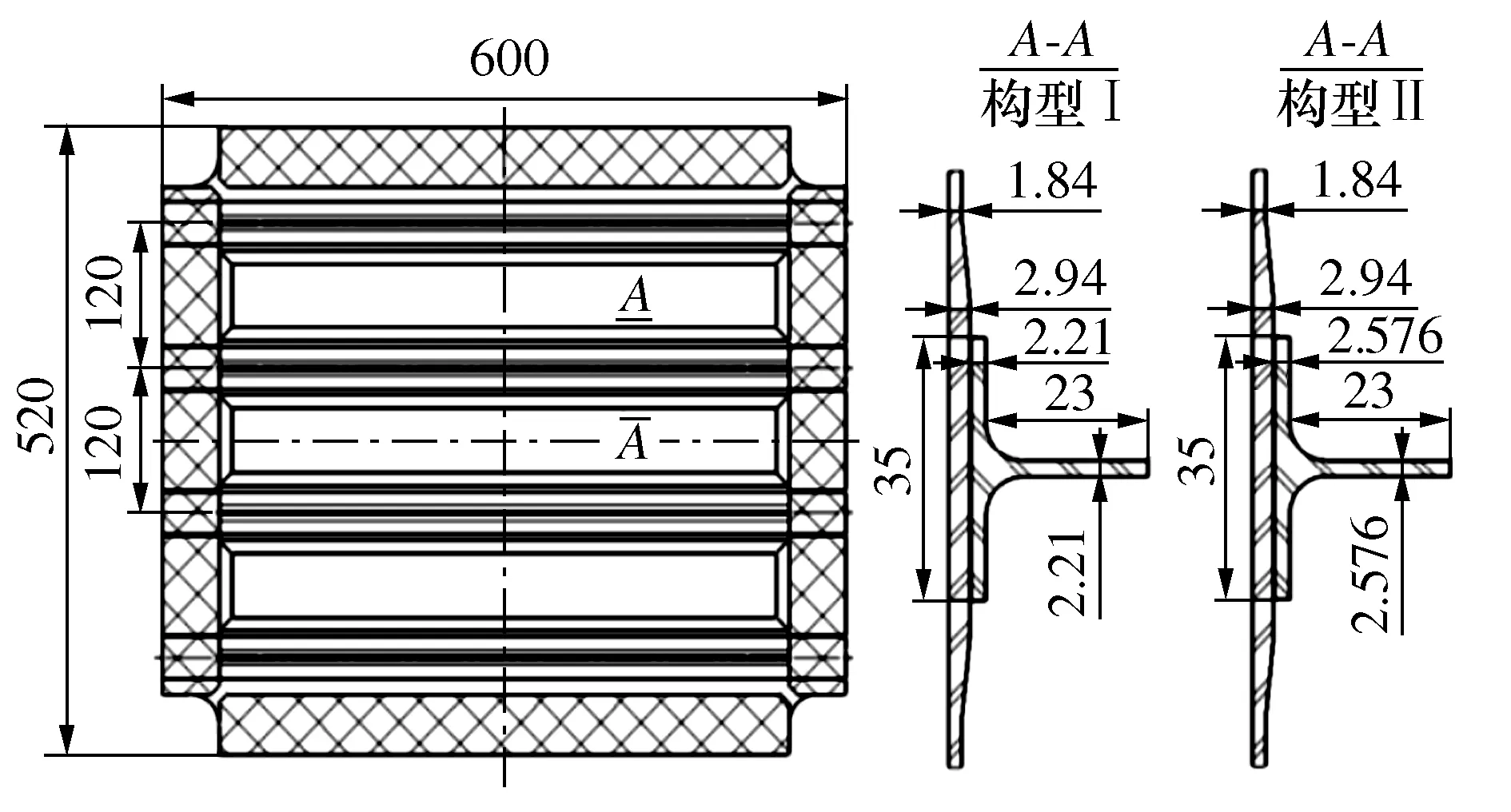
图1 试验件几何参数示意图
2 数值分析
2.1 特征值屈曲分析
特征值屈曲分析以小位移、小应变线弹性理论为基础,分析中不考虑受载变形过程中结构形状的改变,即在外力施加各个阶段,总是在结构初始形状上建立平衡方程,当屈曲产生时,结构形位突然跳到另一个平衡状态。特征值屈曲分析分为两个阶段。
第一阶段为线性静力分析,其表达式为
[Ko]{μ}={p*}
(1)
第二阶段为求解线性方程组,求解特征值λ及相应的特征向量,求解方程组为
([Ko]+λ[KG]){μ}={0}
(2)
式中:[Ko]代表结构的弹性刚度矩阵;[KG]代表几何刚度矩阵;λ代表屈曲载荷系数;{μ}代表位移向量;{p*}为代表载荷向量。用得到λ值乘以外载荷,即可得到屈曲载荷。
2.2 渐进损伤失效分析
渐进损伤失效分析是基于含损伤材料能按材料性能退化后的属性继续承载前提假设进行的计算方法,求解流程包括非线性应力分析求解、材料失效损伤分析与损伤材料性能退化2个阶段[12]。
1) 加筋壁板失效准则及刚度退化准则
承受剪切载荷的加筋壁板主要应力状态为面内剪切。对于加筋壁板面内损伤有多种形式,如基体拉伸/压缩损伤、纤维拉伸/压缩损伤及纤维基体剪切损伤等。为有效考虑材料本构关系及损伤后材料的刚度退化,采用Hashin准则研究剪切载荷作用下的变厚度加筋壁板承载能力。Hashin准则材料失效准则见表3。

表3 复合材料二维Hashin失效准则
当材料出现损伤时,复合材料层压结构本构关系为
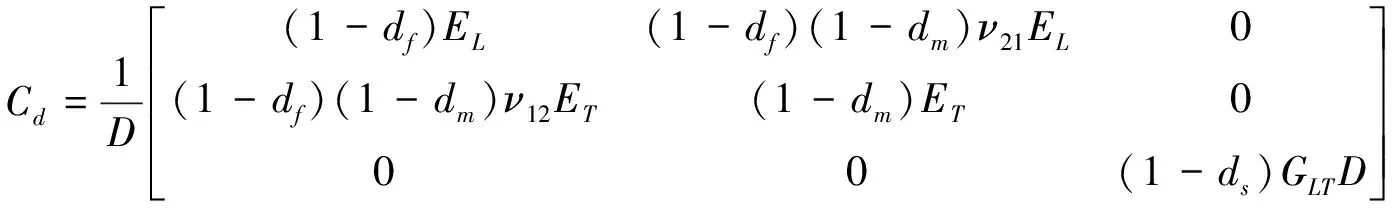
(3)
式中:EL,ET和GLT分别代表拉伸方向模量,压缩方向模量和面内剪切模量;D=1-(1-df)(1-dm)ν12ν21;df、dm和ds分别代表纤维损伤当前状态、基体损伤当前状态和剪切损伤当前状态。
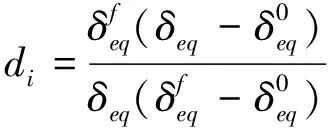
(4)
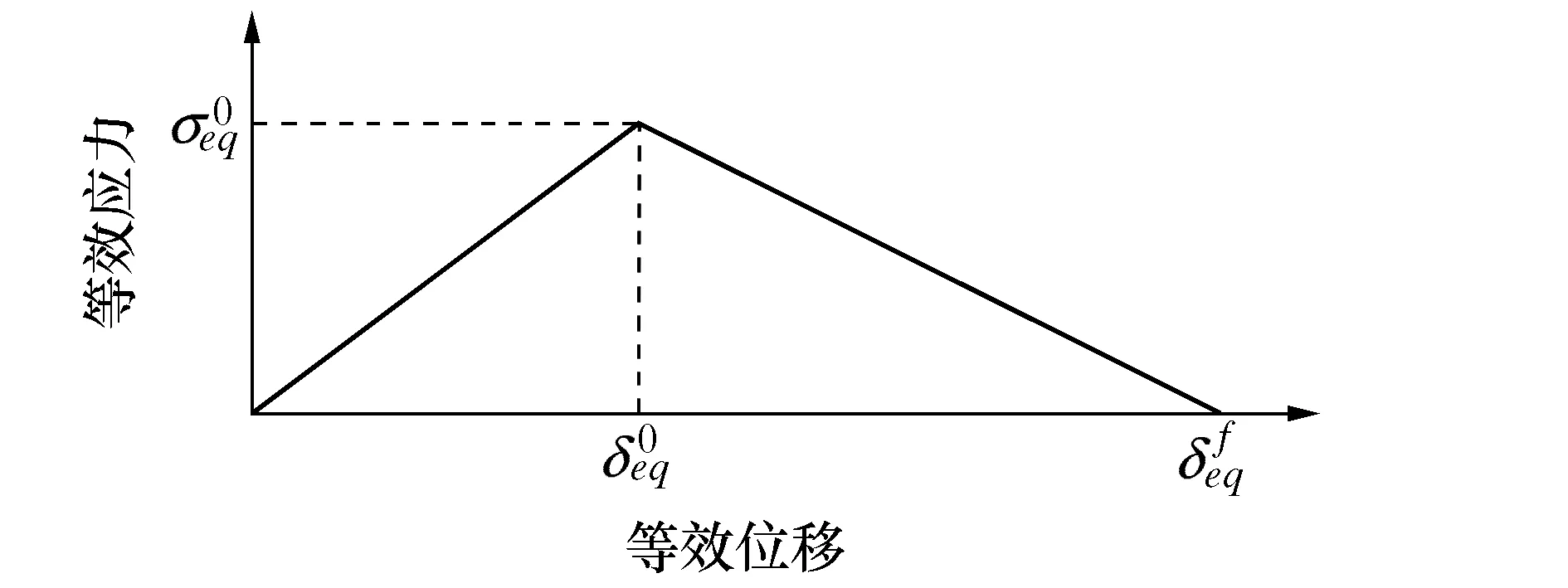
图2 等效应力与等效位移关系
2) 胶接界面失效准则及刚度退化
复合材料加筋壁板蒙皮与长桁胶接界面失效模型采用考虑界面损伤起始和演化的内聚力模型[13-14]。胶接界面单元损伤起始判定准则采用Quadratic失效准则,其表达式为
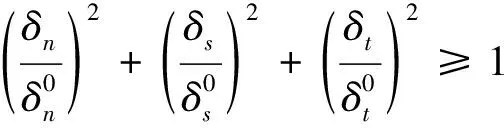
(5)
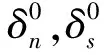
胶接界面单元损伤演化准则采用Benzeggagh-Kenane能量准则,其表达式为
(6)
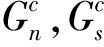
2.3 有限元模型建立
基于有限元软件ABAQUS进行结构建模,复合材料模型单元有Conventional Shell单元、Continuum Shell单元和Solid单元。若采用Conventional Shell单元模拟变厚度复合材料结构,其不能有效反应变厚度区域模型属性;若采用Solid单元模拟变厚度复合材料结构,其模型构建工作量极大,过程繁琐,效率低下,不利于工程大面积应用。鉴于上述原因,本文采用模型构建较Solid单元简单、且能适当反应变厚度区域模型属性的Continuum Shell单元模拟变厚度复合材料结构。
加筋壁板蒙皮和长桁采用Continuum Shell单元SC8R模拟;蒙皮与长桁之间胶接界面采用三维内聚力Cohesive单元COH3D8模拟;Cohesive单元与Continuum Shell单元之间采用Tie多点约束模拟。加筋壁板4个边角位置即试验中连接各夹具的销轴所处位置设置参考点,模型与参考点之间建立属性Link多点约束,用于模拟试验夹具通过螺栓传递给试验件的载荷传递路径。
2.4 计算结果与讨论
1) 特征值屈曲分析结果
对加筋壁板剪切模型进行特征值屈曲分析,加载方式采用对角拉伸位移加载,固定载荷施加100 kN,屈曲载荷施加100 kN。构型I试验件特征值求解屈曲模态见图3。求解一阶特征值为0.77,即1阶屈曲载荷为100 kN+0.77×100 kN=177 kN;构型II试验件特征值求解屈曲模态见图4,求解1阶特征值为0.90,即1阶屈曲载荷为100 kN+0.90×100 kN=190 kN。
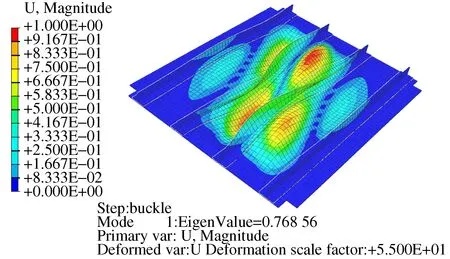
图3 构型I加筋壁板试验件1阶屈曲模态
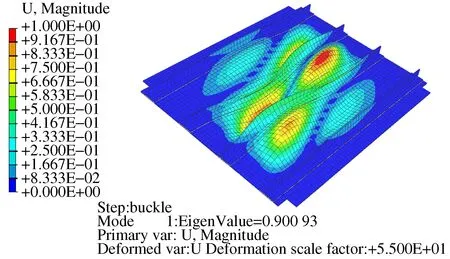
图4 构型II加筋壁板试验件1阶屈曲模态
对比构型I和构型II试验件屈曲载荷值,构型II试验件屈曲载荷较构型I试验件屈曲载荷提高190 kN-177 kN=13 kN,提高百分比为(190 kN-177 kN)/177 kN×100%=7.34%。构型I试验件和构型II试验件加筋壁板蒙皮厚度、铺层信息相同,构型I试验件长桁横截面积占蒙皮百分比48.93%,构型II试验件长桁横截面积占蒙皮百分比56.12%,即构型II试验件长桁横截面积较构型I试验件提高(56.12%-48.93%)/48.93%=14.69%,屈曲载荷提高7.34%。
2) 结构渐进损伤失效计算
构型I和构型II试验件加筋壁板后屈曲承载能力载荷-位移曲线见图5。构型I试验件曲线初始阶段呈线性,载荷加载至180 kN左右时,曲线出现拐点,此时试验件开始出现屈曲,之后曲线曲率下降,进入后屈曲阶段。随着载荷继续增加,最终曲线在248 kN时达到顶点,即结构的承载能力为248 kN;构型II试验件载荷加载至200 kN左右时,曲线出现转折,随着载荷继续增加,最终曲线在260 kN时达到顶点,即结构的承载能力为260 kN。
对比构型I和构型II试验件渐进损伤失效计算结果,构型II试验件承载能力较构型I试验件提高260 kN-248 kN=12 kN,提高百分比为(260 kN-248 kN)/248 kN×100%=4.84%。构型II试验件较构型I试验件长桁横截面积提高14.69%,剪切载荷承载能力提高4.84%。
3 试验验证
3.1 试验支持及加载
试验在YDL-2000电液伺服液压万能试验机(2 000 kN,精度±1%)上进行,应变采用DH3816型60通道高速静态应变仪器测量。试验件四边与夹具通过双剪单排紧固件形式连接,纵横夹具之间通过销轴连接成整体。加载方式采用对角拉伸逐级位移加载方式加载,试验件支持和加载方式见图6。

图6 试验件支持和加载方式
3.2 试验测量及结果
试验件内表面和外表面均布置有应变花片。内表面定义为有长桁一侧,外表面定义为无长桁一侧,贴片位置见图7。考虑复合材料制件工艺分散性,每种构型试验件共计生产3件。图8和图9均为其中一件典型载荷-应变曲线。图7中字母“Z”表示内表面贴片;“B”表示外表面贴片。图8和图9中应变花片编号第一位数字表示此类试验件的组号,第二位表示试验件的顺序号,其余编号表示其所在试验件位置并与图7应变花片对应。
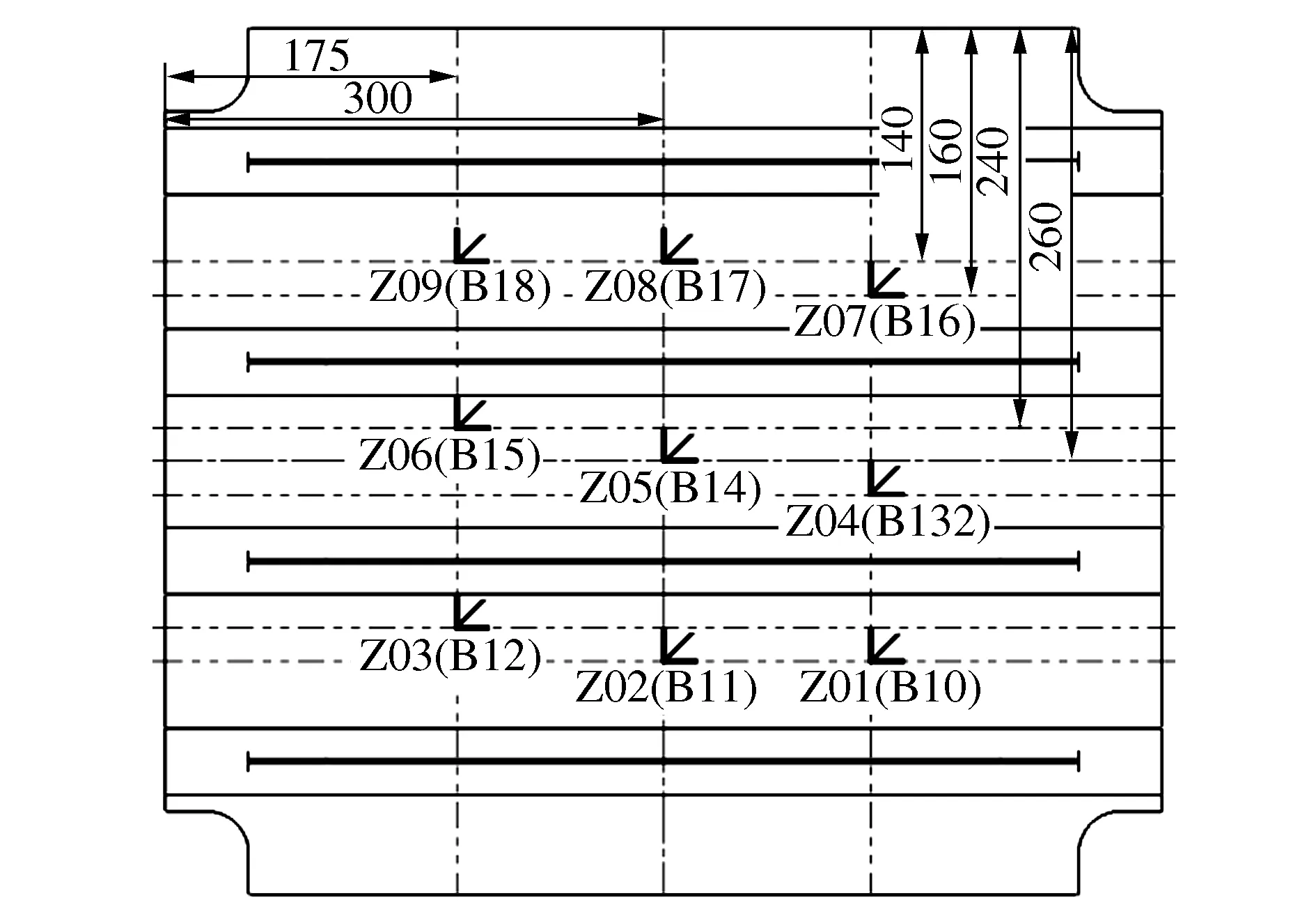
图7 试验件应变花片布置图
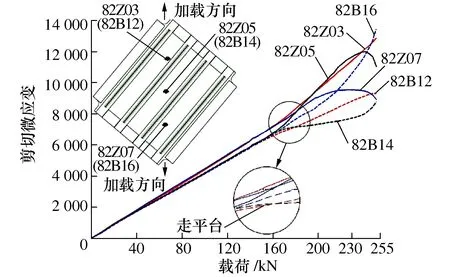
图8 构型I加筋壁板典型载荷-应变曲线图
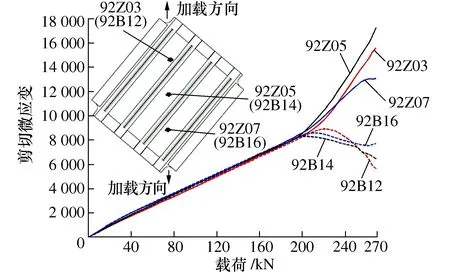
图9 构型II加筋壁板典型载荷-应变曲线图
3.3 计算结果与试验结果对比
选取82Z05(82B14)处剪切微应变计算值和试验值对比,对比结果见图10。图10显示计算曲线和试验曲线趋势一致,表明计算模型及边界条件的选取正确;曲线存在一定偏差,究其原因是试验件制造公差和几何非线性引起的偏离。计算结果与试验结果对比见表4。

图10 剪应变测量值和有限元模拟值对比图
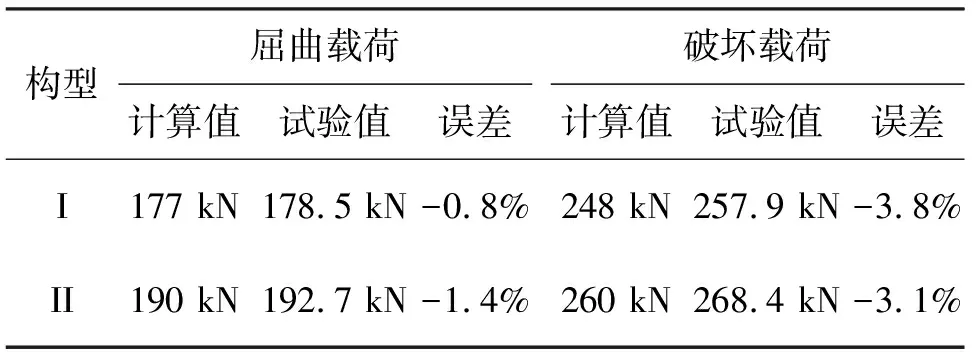
表4 屈曲载荷和破坏载荷计算结果与试验结果对比
通过计算结果与试验结果数据对比表明:
1) 特征值屈曲分析方法和渐进损伤失效分析方法可以准确的预测变厚度加筋壁板剪切屈曲载荷及后屈曲承载载荷。
2) 长桁横截面积几何参数对加筋壁板剪切屈曲载荷及后屈曲承载载荷有一定影响,但是影响效率不高。通过增加长桁横截面积不能有效的提高加筋壁板剪切屈曲载荷及后屈曲承载载荷。
4 结论
1) 加筋壁板采用Continuum Shell单元SC8R模拟、胶接界面采用Cohesive单元COH3D8模拟和试验夹具与试验件之间通过Link多点约束模拟的模型,数值分析值与试验值相对误差不大于4%,即该模型构建和边界条件模拟方法可以准确预测其屈曲载荷和后屈曲载荷。
2) 长桁横截面积提高14.69%,屈曲载荷和后屈曲载荷分别提高7.34%和4.84%,即长桁横截面积对加筋壁板剪切屈曲载荷及后屈曲承载载荷有一定影响,但是影响效率不高。
3) 两种构型加筋壁板后屈曲载荷较屈曲载荷分别提高44.48%和39.28%,即加筋壁板剪切屈曲后仍然具有一定后屈曲承载能力。
