复合材料齿轮的接触和弯曲应力分析
2022-05-20刘峰峰王旭鹏刘舒伟张卫亮唐欣尧薛藤元
刘峰峰,王旭鹏*,,,刘舒伟,张卫亮,唐欣尧,薛藤元
(1. 西安理工大学 军民融合助力与防护装备设计创新研究中心,西安 710054;2. 西安理工大学 机械与精密仪器工程学院,西安 710048)
在航空航天、军用装备等领域,齿轮的轻量化设计要求十分严格。因此,齿轮的减重设计具有重要意义[1-2]。齿轮减重最普遍的方法是去除齿轮本体材料[3],但这可能会引入额外的动态激励并增加机械系统的振动行为。目前较流行的方法是采用复合材料或混合金属复合材料设计来进行齿轮减重[4-5]。玻璃纤维、碳纤维等纤维增强复合材料具有高比强、高比模的优点,在减重设计方面具有较大优势。此外,选择合适的基体材料制备复合材料齿轮能够提升齿轮啮合过程中对齿间冲击行为的吸收能力[6]。因此,近年来众多学者在纤维增强复合材料齿轮的设计制备及其承载能力方面进行了大量研究。
Handschuh等[7]以三轴编织复合材料替代金属材料进行齿轮中心腹板设计,该齿轮在不牺牲强度的前提下实现了减重20%的成效。Catera等[8]提出了一种预测混合材料齿轮固有频率的方法,该方法基于多尺度复合材料建模,以代表性体积单胞方法预测齿轮中心腹板的力学性能,并使用有限元法进行齿轮的模态分析。随后,Catera等[9]分别采用均匀化方法及逐层计算方法研究金属-铺层复合材料齿轮啮合的传动误差及啮合刚度,发现混合材料齿轮在传动误差及啮合刚度上均优于金属材料齿轮。Waller等[10]研究了多种纤维增强的金属混合材料齿轮的弯曲强度及纤维复合材料层板对于载荷的分担效应。Kini等[11]在齿轮齿面引入复合材料织物,得出复合材料织物包层存在一个最优抛物线齿冠形和最优厚度,使齿轮在啮合过程中的接触和弯曲应力最小。
本文在考虑了编织复合材料的编织角、纤维束截面形状的基础上,提出了一种三维五向编织复合材料齿轮的参数化设计方法,采用均质化思想建立了复合材料与齿轮力学性能间的联系,并对复合材料齿轮啮合过程进行了数值模拟。
1 复合材料参数化建模及性能分析
1.1 三维五向编织复合材料参数化模型
三维五向编织复合材料在细观层面具有周期性特点,因此可以采用代表性体积单胞预测材料的宏观力学性能。文献[12]指出三维五向编织复合材料的力学性能主要取决于内胞的力学性能,因此本文忽略了面胞和角胞。本文根据四步法1×1编织方法,给出了内胞的拓扑结构模型,如图1所示,图中W、T、h分别为内胞几何模型的宽度、厚度、高度,γ为内部编织角。

图1 内胞拓扑结构模型
张典堂在获取三维五向编织复合材料样件截面图像的基础上,考虑了纱线间的相互作用,建立了三维五向编织复合材料编织工艺参数与单胞几何模型参数间的数学模型[13]:
(1)
(2)
(3)
Sa=e2
(4)
(5)
(6)
(7)
(8)
式中:Sa、Sb分别为轴纱、编织纱横截面面积;λa、λb、ρa、ρb分别为轴纱线密度、编织纱线密度、轴纱体积密度、编织纱体积密度;εa、εb分别为轴纱、编织纱填充因子,填充因子为纤维在纱线中的体积占比;k、θ分别为编织纱截面宽度和顶角角度;e为轴纱横截面边长;α、γ分别为编织角、内部编织角。图2给出了纱线的截面形状。

图2 纱线截面形状
根据上述给出的内胞拓扑结构模型及参数间的数学模型,建立了编织角为45°的内胞几何模型,如图3所示。

图3 45°编织角单胞模型
1.2 复合材料力学性能分析
1.2.1 周期性边界条件
对于含周期性单胞结构的三维编织复合材料,使用有限元方法进行单胞模型的力学响应时,施加合理的边界条件是获得准确力学响应结果的基础。目前,学者们多采用周期性边界条件来保证相邻单胞边界处的变形协调和应力连续。Xia给出了立方体单胞模型相对边界面上的位移公式[14],即:
(9)
(10)
(11)

i,j=1,2,3
(12)


图4 单胞周期性网格模型
1.2.2 复合材料弹性性能预测
基于均匀化方法预测复合材料宏观尺度上的弹性性能,单胞结构在位移边界条件下的材料本构关系为
(13)

(14)
(15)
式中V为立方体单胞体积。

(16)
本文以T300纤维及PEEK基体作为复合材料的组分材料,材料属性见表1,其中Ef1、Ef2、Gf12、Gf23分别为纤维纵向拉伸模量、横向拉伸模量、纵向剪切模量及横向剪切模量,Em、Gm分别为基体拉伸模量和剪切模量;v12、vm分别为纤维和基体的泊松比;Vf、ρ分别为组分材料的体积含量和体积密度。根据表1中组分材料的体积含量及体积密度可以计算出复合材料齿轮体积密度为1.54 g/cm3,而传统金属材料齿轮密度一般在8 g/cm3左右,显然三维编织复合材料齿轮较金属材料齿轮在重量上具有较大优势。

表1 组分材料属性
图5为内胞模型力学响应的有限元求解结果,图5a)、图5b)分别为单胞模型在1方向拉伸、12方向剪切位移载荷下的应力结果。

图5 不同载荷下有限元模型的应力结果
在获得有限元求解结果后,利用Python脚本语言提取有限元模型结果上各网格单元体积与积分点处应力应变值,计算得到平均应力与平均应变,代入式(16)求解出材料的弹性常数。表2给出了预测的45°编织角三维五向编织复合材料的弹性常数,并且与试验数据进行了对比验证,预测数值与试验数据吻合良好,表明了该方法的准确性。

表2 45°编织角三维五向复合材料弹性常数预测结果
2 复合材料齿轮承载能力分析
齿轮在低周载荷下易产生齿顶点蚀及齿根折断的失效模式。齿顶点蚀是由啮合过程中啮合处多次重复的交变接触应力所造成,而轮齿折断是由多次重复的弯曲应力和应力集中造成。分析复合材料齿轮啮合过程中接触应力与弯曲应力的分布情况对于预防齿轮疲劳失效具有重要意义。
2.1 复合材料齿轮有限元模型
三维五向编织复合材料齿轮的制备流程为:采用1×1的矩形四步法编织得到纤维束编织预制体,浸入基体中经过高温固化等工艺制备得到复合材料齿轮初始样件,最后经过机械裁减获得齿轮零件,具体流程见图6。此外,由于三维五向编织复合材料为横观各向同性材料,为保证复合材料齿轮在啮合过程中的均匀承载,制备齿轮时选择材料2、3主轴方向为齿轮面内方向,1方向为齿宽方向。

图6 三维五向编织复合材料齿轮制备流程
在以均质化思想获得复合材料齿轮力学性能的基础上,使用有限元方法分析复合材料齿轮啮合过程中的应力分布情况。商业有限元软件Abaqus对于非线性问题求解具有较高的认可度,因此本文选择在Abaqus/Standard中进行复合材料齿轮动态啮合过程问题的求解。不过Abaqus建立复杂几何模型的能力较差,因此在Creo7.0中完成了齿轮副几何模型的构建,并忽略了齿轮的小孔特征。表3给出了算例齿轮的参数。在构建有限元模型时,为控制计算成本,选取六齿模型进行网格划分,对接触区域进行网格加密,且经过试算得到该网格密度对于接触应力数值结果的求解已趋于稳定。

表3 算例齿轮基本参数
网格模型如图7所示,网格单元类型为C3D8R,节点数为642 964,单元数为590 080。根据齿轮制备时的纤维材料方向,设定齿宽方向为材料主轴1方向,齿轮面内为材料主轴的2、3方向。

图7 六齿齿轮网格模型
为便于施加载荷及约束,在齿轮孔内壁与孔中心之间建立刚性元,在Abaqus中实施为孔内壁表面与孔中心参考点(RP-1、RP-2)建立耦合约束[15]。建立的刚性元远离齿轮,对齿轮应力分布的影响可以忽略。并且在两个齿轮可能接触的齿面上建立接触关系,接触设定选择Finite sliding的接触面滑动方式以及Surface to Surface的离散方法。耦合约束及接触面设定见图8。此外,忽略啮合过程中齿面间的摩擦行为,并且设定法向接触属性为硬接触。对于边界条件及载荷,保留主动轮与从动轮齿在齿轮啮合转动方向的自由度,主动轮施加恒定角速度,从动轮施加恒定转矩。
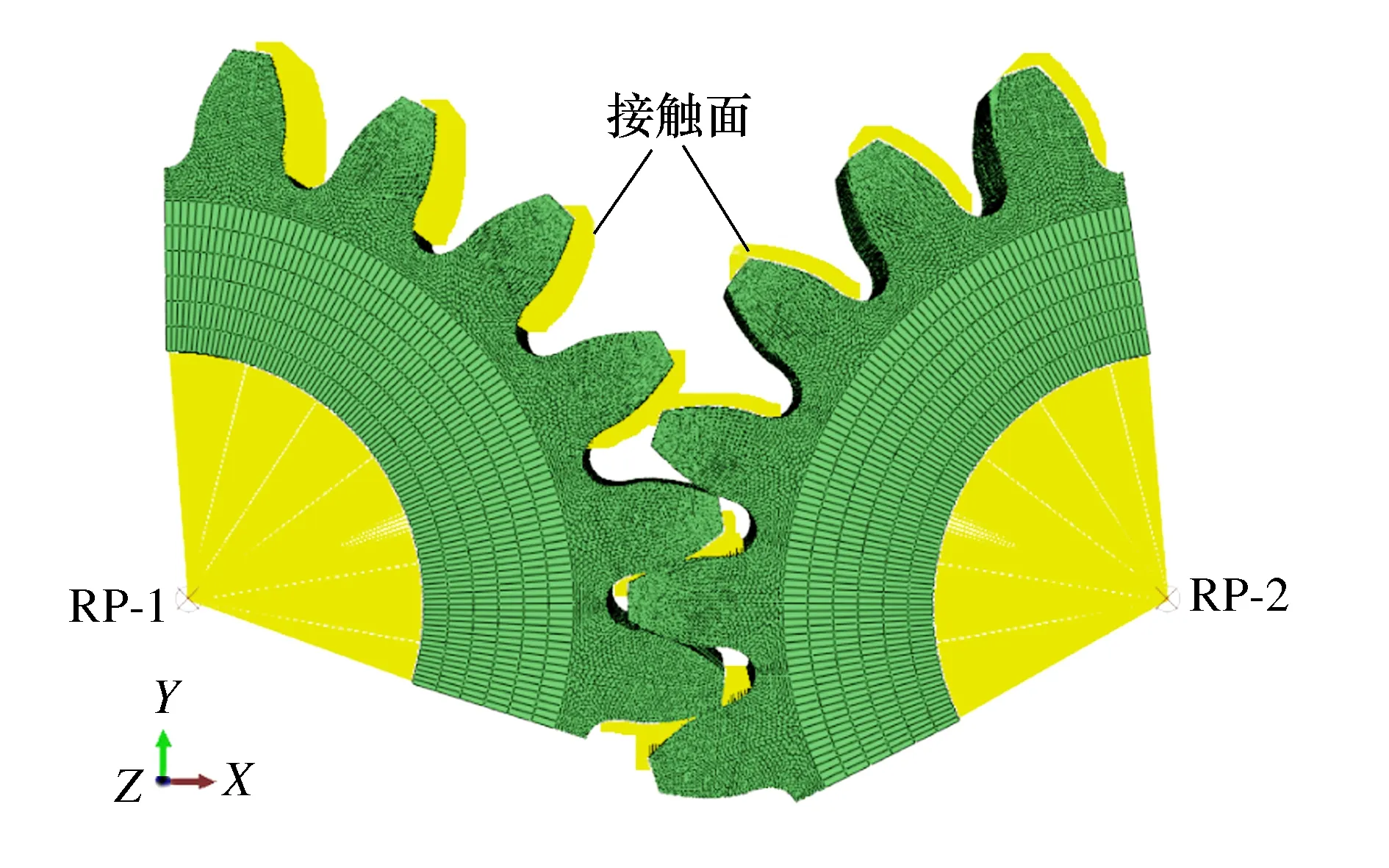
图8 耦合约束及接触面设定
2.2 复合材料齿轮接触应力
根据有限元模型计算结果,给出了关键啮合时刻的Mises应力云图,如图9所示。此外,提取单齿从啮入到啮出一个周期内的接触应力数据,绘制100 Nm转矩下轮齿啮合最大接触应力变化曲线如图10所示。

图9 关键啮合时刻Mises应力云图

图10 100 Nm转矩下轮齿啮合最大接触应力变化曲线
由图10可知,齿轮啮合呈现出双齿啮合和单齿啮合两阶段交替的周期性,且在双齿啮合和单齿啮合的交替时刻,存在齿顶与齿根之间的边缘接触区域,该区域产生了应力集中现象,应力数值为227.1 MPa,如图11所示。在不考虑边缘接触产生的应力集中的情况下,单齿啮合阶段的接触应力明显高于双齿啮合阶段,因此应该重点关注单齿啮合阶段的接触应力情况;由图10可知,轮齿在单齿啮合阶段存在接触疲劳危险点,该点接触应力为165.7 MPa,图12给出了该点的接触应力云图。

图11 边缘接触位置应力集中
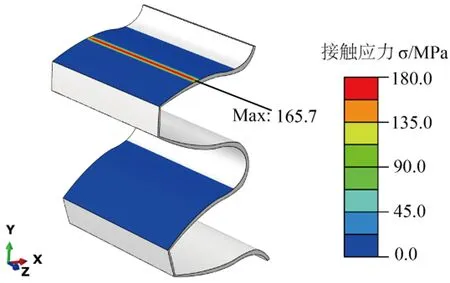
图12 接触疲劳危险点处接触应力
为定量研究加载条件与复合材料齿轮啮合接触应力间的数值关系,对不同转矩条件下的齿轮啮合过程进行有限元计算,施加了8组不同的转矩,根据计算结果绘制转矩与接触应力变化曲线如图13所示。

图13 转矩与接触应力变化曲线
由图13可知,最大接触应力随着转矩的增大而增大,但是增大的幅度呈现出逐渐减小的趋势。这是因为对弹性体而言,载荷增大的同时也导致了接触面积的增大。该现象符合赫兹接触规律。
2.3 复合材料齿轮弯曲应力
提取齿轮接触区域外的Mises应力得到齿轮啮合弯曲应力数据,绘制弯曲应力变化曲线如图14所示。

图14 齿轮啮合过程最大弯曲应力变化曲线
由图14可知,主动轮与从动轮在单齿啮合阶段的弯曲应力明显大于双齿啮合阶段,且最大弯曲应力出现在双齿啮合与单齿啮合的交替时刻,不过主动轮最大弯曲应力出现在单齿啮合到双齿啮合的交替点,该点为主动轮齿的啮入点,而从动轮恰好相反,出现在双齿啮合到单齿啮合的交替点,该点为主动轮齿的啮出点;这是因为在单齿啮合阶段,啮合点在主动轮上由齿根向齿顶方向移动,在从动轮上由齿顶向齿根方向移动,随着啮合位置的改变,主动轮、从动轮齿根处与啮合点之间的距离即力矩产生改变,而从动轮在单齿啮合初始时刻力矩最大,因此弯曲应力峰值出现在该时刻,此后则呈现处逐渐下降的趋势,而主动轮弯曲应力峰值出现在单齿啮合结束时刻,因此在单齿啮合阶段内弯曲应力一直呈现上升的趋势;主动轮受到最大弯曲应力为51.3 MPa,从动轮为54.1 MPa,且均位于齿根过渡圆弧区域,该区域易发生弯曲疲劳断裂,如图15、图16所示。

图15 主动轮最大弯曲应力
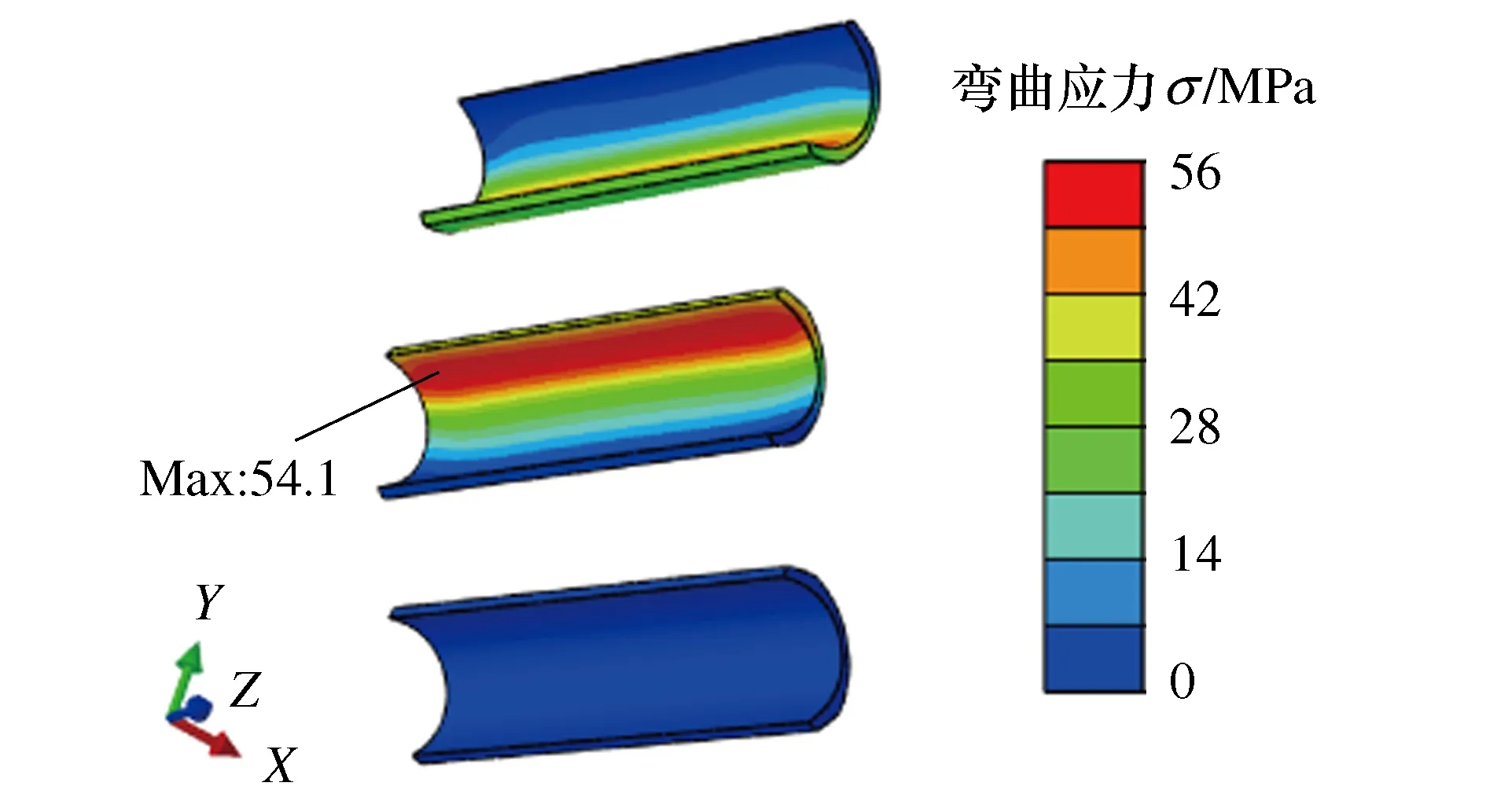
图16 从动轮最大弯曲应力
同样地对加载条件与齿轮啮合弯曲应力的数值关系进行研究,绘制转矩与弯曲应力变化曲线如图17所示。
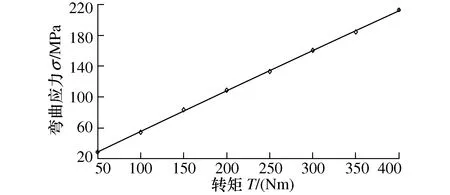
图17 转矩与弯曲应力变化曲线
由图17可知,最大弯曲应力与转矩之间呈线性关系,这与GB/T 3480.3-2021(直齿轮和斜齿轮承载能力计算第3部分:轮齿弯曲强度计算)计算相符。
3 结论
1) 齿轮正常啮合过程中,最大接触应力出现在单齿啮合阶段,此时齿轮易发生疲劳磨损。
2) 弯曲疲劳危险点出现在双齿啮合与单齿啮合阶段的交替时刻,此时最易发生轮齿疲劳折断,其中主动轮的弯曲疲劳危险点出现在单齿啮合结束时刻,从动轮出现在单齿啮合初始时刻。
3) 在齿轮开始啮合时,即主动轮齿根刚接触到从动轮齿顶,存在应力集中现象,必须对从动齿轮进行齿顶修缘以减少应力集中现象。
4) 接触应力峰值与转矩之间的函数关系符合赫兹接触规律;弯曲应力峰值与转矩呈线性关系。
