电动闸阀温度场有限元仿真分析研究
2022-05-20沈云海谭术洋吴广皓王保平
沈云海 谭术洋 周 宁 吴广皓 王保平
(中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610213)
0 引言
电动闸阀通过电动执行器实现阀门的开和关,电动闸阀因其响应灵敏、安全可靠、开关速度可以调整、结构简单、易维护等优点在工业界被广泛应用。在高温介质条件下的电动闸阀的电动装置,承受来自流体的热传导,同时受到电机回转自身产生的热作用,容易出现超温而导致电动装置故障。对电动闸阀整体温度场进行定量预估将有助于电动阀门的优化设计,特别是对于控制电动装置温度、延长电动装置寿命有重要作用。
本文在技术要求规定的工况下采用有限元软件对电动闸阀进行热分析计算,通过计算所需运行工况下电动闸阀电动装置将达到的运行环境温度,验证其电动装置温度参数选型的合理性。
1 电动闸阀温度场研究方法
1.1 电动闸阀温度场研究概述
电动闸阀温度场的研究方法可归纳为实验研究、数值模拟、理论计算三种类型。如图1 所示,实验研究准确,但可获得的信息量较小;理论分析可分析变量间的相互关联及影响,但存在对复杂系统、多变量问题很难给出明确关联式的弊端; 数值模拟法具备求解多变量复杂系统的突出优势,且可得到时间与空间中任一点的变化趋势,但是数值计算的结果还需要由实验进行验证。
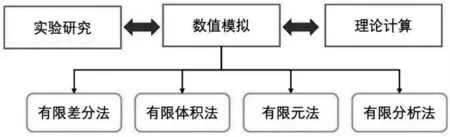
图1 温度场的研究方法
综合来看,三种方法各有其适用范围,把这三种研究方法结合起来是研究传热问题理想而有效的手段,可以起到互相补充、相得益彰的作用。
1.2 电动闸阀温度场的数学描述
一个物体的温度场可表示为(,,,τ)的函数,建立一个导热过程的数学描述(即导热数学模型)也就是确立函数(,,,τ)的具体表达式。
再假设:(1)所研究的物体由各向同性的连续介质构成;(2)物体导热过程可由傅立叶导热定律描述的条件下,物体的三维非稳态导热数学模型(即微分方程)可由公式(1)表述。

式中,α=λ/,称为热扩散率,也称导温系数,单位为km/s。Φ 为内热源强度,单位为W/m,表示单位时间、单位体积内的内热源生成热。
对导热过程完整的数学描述,不仅应有导热微分方程式,还需要有导热边界条件,两者共同构成了导热过程的完整表述。与导热微分方程相配套的热边界条件有三类。
1.2.1 第一类边界条件
给出物体边界上的温度分布及其随时间变化的规律:

如果在整个导热过程中物体边界上的温度为定值,则公式(2)简化为:

1.2.2 第二类边界条件
第二类边界条件给出物体边界上的热流密度分布及其随时间变化的规律:

根据傅里叶定律:

可得第二类边界条件的计算式:

第二类边界条件给出了边界面法线方向的温度变化率,但边界温度未知。如果在导热过程中,物体的某一表面是绝热的,即q=0,则有:

1.2.3 第三类边界条件
第三类边界条件给出了与物体表面进行对流传热的流体的温度t及表面传热系数。
根据边界面的热平衡,由物体内部导向边界面的热流密度应该等于从边界面传给周围流体的热流密度,于是由傅里叶定律和牛顿冷却公式可得:

该式建立了物体温度场在边界处的变化率与边界处对流传热之间的关系,所以第三类边界条件也称为对流传热边界条件。
上述三类边界条件概括了导热问题中的大部分实际情况,并且都是线性的,所以也称为线性边界条件。如果导热物体的边界处除了对流传热外,还存在与周围环境之间的辐射传热,则物体边界面的热平衡表达式为:

式中,q为物体边界面与周围环境之间的净辐射传热热流密度,q与物体边界面和周围环境温度的四次方有关。由于物体边界面与周围环境的辐射特性有关,所以式(9)是温度的复杂函数。这种对流传热与辐射传热叠加的边界条件形成了非线性复合传热边界条件。
1.3 电动闸阀温度场的数值求解方法
采用计算机求解流动与传热问题的控制方程的方法又称为数值传热学 (Numerical Heat Transfer,NHT) 或计算传热学 (Computational Heat Transfer,CHT)。它是传热学与数值方法相结合的一门交叉学科。数值传热学的基本思想是把原来在空间与时间坐标中连续的物理量的场(如速度场、温度场、浓度场等),用一系列有限个离散点(称为节点)的值的集合来代替,通过一定的原则建立起这些离散点变量值之间的关系的代数方程 (称为离散方程,discretization equation),求解所建立起来的代数方程以获得求解变量的近似值。
传热过程数值计算的方法可分为有限差分法、有限容积法、有限元法、有限分析法等多种。
在涉及流动及传热计算中以ANSYS 为代表的商用软件成为流动及传热计算的主流,ANSYS 所包含的以限元为代表的经典ANSYS 及后收购的以有限体积法为代表的CFX 或FLUENT 模块可实现复杂条件下多物理场流固耦合计算。针对固体传热计算,有以ANSYS 为代表的有限元法和以CFX 或FLUENT 为代表的有限体积法,尽管两种方法在离散导热计算上采用了不同的方法,但是经过多年的发展,实践表明,二者在计算精度上并无明显差别。
2 电动闸阀热分析模型
热量以传导、对流、辐射三种方式进行传递,为了便于计算电动闸阀顶端的电动装置温度,有必要对电动闸阀的热量传递过程进行分析。
(1)流经管道与阀门的高温水以对流换热的形式将热量传递给阀体内壁;(2) 阀体内壁的热量以热传导的形式将热量传递给阀体外壁,同时热量以热传导的方式,通过阀杆向阀门上部,即电动装置一端进行传导;(3)在阀门外壁与空气接触侧,热量将以对流和辐射的形式向外部空间散热;(4)阀门工作一段时间后,热量的传递与散失将会达到平衡状态,最终温度场趋于恒定,也称之为稳态导热阶段。
在这一传热过程中,给定准确的材料热物性参数是获得可靠温度场的基础,确定流体与固体侧热触的对流换热系数是计算阀门电动装置温度场的关键。
本次数值模拟面临的主要问题是电动闸阀结构复杂,涉及多种材料及复杂的装配结构,如用实物模型直接模拟计算,会出现网格畸变等问题,考虑到本次计算的目的是预测电动装置可能出现的最大温度,为了简化计算,也为了提高计算的准确度,确定如下计算原则:
以提高计算准确度为原则,在对不确定零件进行简化时,以可能导致电动装置出现较高温度为原则。换言之,数值模拟温度场应尽量准确,但计算误差应控制为正误差,数值模拟计算出的电动装置温度应宁高勿低,这样的计算结果偏于保守,但对于工程设计具有明确的指导意义。
在此原则下确立如下简化方案:
不考虑两个物体交接面的接触热阻。
不考虑垫片与相接触的金属材料的导热性能差异,将垫片材料设定为与之接触的较高导热性能的金属。
模型中删除导角、细小突台等小尺寸结构,以改善网格质量,提高计算准确度。
综上,电动闸阀由阀体、阀盖、丝杠螺母、滚珠丝杠、阀杆和闸板等组成。电动闸阀的三维模型如图2所示。电动闸阀的有限元模型主要用来分析电动闸阀在设计说明书规定的不同工况作用下的温度场分布情况,为电动闸阀的设计提供依据。

图2 电动闸阀三维几何模型
2.1 电动闸阀的有限元模型
利用有限元软件建立电动闸阀三维有限元网格模型。为了保证计算精度,提前进行了网格无关性验证,验证结果显示,网格尺寸为7 mm 时计算结果最为合理,因此设定网格尺寸为7 mm 对电动闸阀进行网格划分,网格数量为851 746 个,节点数为1 278 072 个。
2.2 固体材料物性参数
各主要零部件所用材料及材料特性如表1 所示。

表1 零部件所用材料属性
2.3 流体介质物性参数
(1)350℃饱和水的物性参数:
温度=350℃
饱和蒸气压=16.538 MPa
密度ρ=574.4 kg/m
导热系数λ=0.43 W/(m·k)
普朗特数=1.6
运动黏度=1.26×10m/s
(2)25°空气的物性参数:
温度=25℃
密度ρ=1.185 kg/m
导热系数λ=2.63×10W/(m·k)
黏度μ=18.35×10Pa·s
普兰德数=0.702
2.4 阀门特征参数
管道外径=0.15 m
管道内径=0.11 m
特征长度=2.363 m
管道内流体流速:=6~7 m/s
计算中取=6.5 m/s
2.5 对流换热系数
2.5.1 管内强制对流换热系数
管内流体流动形态的确定:
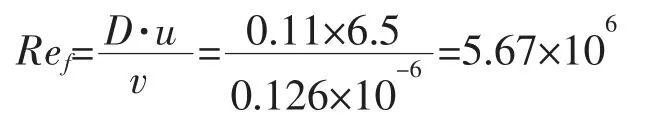
对流换热系数计算公式有多位学者进行过研究,各自提出了不同适用范围的对流换热计算公式,但数量级均相同。考虑到Gnielinski 公式拟合的雷诺数范围与本次计算相接近,故采用Gnielinski 公式拟合结果作为本次计算参数,取为:=7.97×10W/(m·k)。
2.5.2 阀体上腔内部对流换热系数的确定
阀体内部上腔流体速度低于主管道内的流速,该区域对流换热系数小于高雷诺数下的管道强制对流换热系数,具体数值由图3 查取。

图3 过渡区对流换热系数表
依据以往闸阀流场速度计算结果,本次计算取竖圆管管内对流换热系数:
=1.5×10W/(m·k)
2.5.3 阀外部自然对流换热系数确定
电动闸阀为T 型结构,将其简化为直管段与竖圆柱两部分,其对流换热系数各不相同,计算如下:
(1)竖圆柱的计算
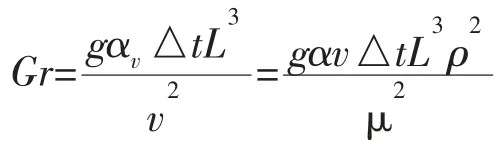
其中,为重力加速度,取=9.8;
为竖圆柱高度,=1.234 m。
将空气近似看作理想气体时:

查表得到25℃空气的物性参数:
温度=25℃,密度ρ=1.185 kg/m
导热系数λ=2.63×10W/(m·k)
黏度μ=18.35×10Pa·s
普朗特数=0.702
Δ=350-25=325℃
计算可得,=1.52×10。
故选择湍流计算式,取=0.0135,=0.43,可得N=(GP)=548.12
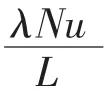
(2)直管段横圆柱的计算


3 电动闸阀热分析计算结果
根据具体电动闸阀的实际工况以及分析特征,对电动闸阀进行稳态热分析计算。
3.1 内部流体为350℃和环境温度为25℃的温度场计算结果
电动闸阀的稳态温度场整体计算结果如图4、图5 和图6 所示。显然,当管道内部流体温度为350℃时,管道壁面的平均温度为339℃,阀盖外表面的平均温度为288℃,与电动装置连接处阀盖法兰的平均温度为108℃,电动装置的平均温度为75℃。由此可知,由管道至电动装置处的温度场分布结果呈现出明显下降的趋势,且接近电动装置处的温度差值最大,其值为33℃。

图4 电动闸阀整体温度场结果云图

图5 电动闸阀纵向截面温度场结果云图

图6 电动闸阀横向截面温度场结果云图
电动闸阀的电动装置顶部、中部和底部的温度场计算结果云图分别如图7、图8 和图9 所示。显然,电动装置顶部平均温度为66℃,中部平均温度为76℃,底部平均温度为95℃。

图7 电动闸阀电动装置顶部截面温度场结果云图

图8 电动闸阀电动装置中部截面温度场结果云图
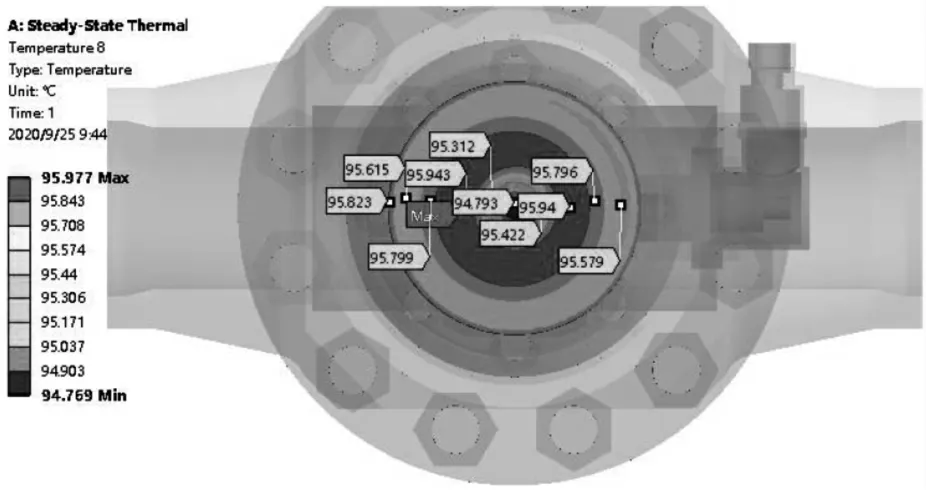
图9 电动闸阀电动装置底部截面温度场结果云图
3.2 内部流体为265℃和环境温度为180℃的温度场计算结果
电动闸阀的稳态温度场整体计算结果如图10、图11 和图12 所示。显然,当管道内部流体温度为265℃,环境温度为180℃时,管道壁面的平均温度为262℃,阀盖外表面的平均温度为253℃,与电动装置连接处阀盖法兰的平均温度为199℃,电动装置的平均温度为193℃。由此可知,由管道至电动装置处的温度场分布结果呈现出明显下降的趋势,且接近电动装置处的温度差值最大,其值为6℃。

图10 电动闸阀整体温度场结果云图

图11 电动闸阀纵向截面温度场结果云图

图12 电动闸阀横向截面温度场结果云图
电动闸阀的电动装置顶部、中部和底部的温度场计算结果云图分别如图13、图14 和图15 所示。显然,电动装置顶部平均温度为191℃,中部平均温度为193℃,底部平均温度为198℃。此外,电动装置凸台处的存在加速了电动装置凸台侧的散热速率,使得电动装置近凸台区域的温度明显低于其他区域。

图13 电动闸阀电动装置顶部截面温度场结果云图

图14 电动闸阀电动装置中部截面温度场结果云图

图15 电动闸阀电动装置底部截面温度场结果云图
4 结语
计算结果表明,电动闸阀在设计说明书规定的工况下,通过有限元仿真软件分析电动闸阀有限元模型的温度场结果可知:
(1)当环境温度为25℃和管道内部流体介质温度为350℃时,电动闸阀竖向阀体外表面换热系数为9.59 W/(m·k),横向管道外表面换热系数为8.403 W/(m·k)。
(2)当环境温度为25℃和管道内部流体介质温度为350℃时,管道壁面的平均温度为339℃,阀盖外表面的平均温度为288℃,与电动装置连接处阀盖法兰的平均温度为108℃,电动装置的平均温度为75℃。
(3)当环境温度为180℃和管道内部流体介质温度为265℃时,管道壁面的平均温度为262℃,阀盖外表面的平均温度为253℃,与电动装置连接处阀盖法兰的平均温度为199℃,电动装置的平均温度为193℃。
综上,在所需运行工况下,电动闸阀的电动装置所处环境温度能够满足低于电动装置最高运行环境温度为220℃的基本要求,因此电动闸阀能够保证可靠运行,执行所需功能。
