燃料元件棒束通道横流特性数值研究

于德勇 曹思民 杜 枢 韩元吉

（中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610213）

0 引言

棒束燃料元件在核能领域得到普遍应用，棒束通道内热工水力研究是堆芯热工安全关注的重点。目前棒束通道内热工水力的研究主要集中在定位格架对流动及搅混特性的影响方面，包括实验与数值研究等。和搅混过程相比，棒束横流特性不仅影响子通道能量输运，还将引起净质量转移，因此棒束的横流特性十分关键，尤其是横流阻力系数是子通道分析的关键封闭模型。

棒束通道热工水力研究主要包括实验研究与数值模拟等，实验研究一方面可真实反映棒束通道流动特性，另一方面可为数值模拟结果提供必要数据验证与支撑，可作为数值模拟计算基准题。然而实验研究成本较高且周期长，因此，经过验证的数值模拟方法越来越广泛地应用于棒束通道热工水力分析。本文选用STAR-CCM+10.04 软件，构建棒束燃料元件通道横流分析模型，通过相应数值模拟，揭示了棒束横流流动特性，拟合得到横流阻力系数计算关系式。本文的研究可为燃料组件子通道分析及实验研究提供参考。

1 数值计算方法

本研究采用STAR-CCM+10.04 软件针对 正方形排列的棒束通道内横流开展数值模拟，计算的几何模型如图1 所示。棒直径为9.5 mm，棒中心间距为12.6 mm，子通道水力直径为10.3 mm，流道高度为100 mm。单相流体由图1 左侧进入，主流方向与棒束垂直。所用工质为水，流动状态为绝热不可压缩，壁面无滑移。系统压力为15 Mpa，环境温度为300℃，入口流速范围为0.1～2 m/s。为保证进口与出口段流体可以充分发展，在进口与出口设置了100 mm 长的延长段。

图1 数值计算几何模型

1.1 网格划分方法

本文采用六面体结构化网格进行建模。考虑到棒束中心通道棒间隙为3.1 mm，边通道棒间隙为1.75 mm，网格划分按照基本尺寸为0.4 mm、0.5 mm、0.6 mm 和0.7 mm 四种网格方案进行筛选。基于出口区域平均压力和速度数值的对比可以发现，在网格基本尺寸为0.5 mm 时，数值已经趋于稳定，如图2 所示，因此数值模拟选取0.5 mm 的网格尺寸方案进行计算。图3 给出了中心通道与边通道的网格场景，该种方案在最小间隙处也有充足的网格布置。

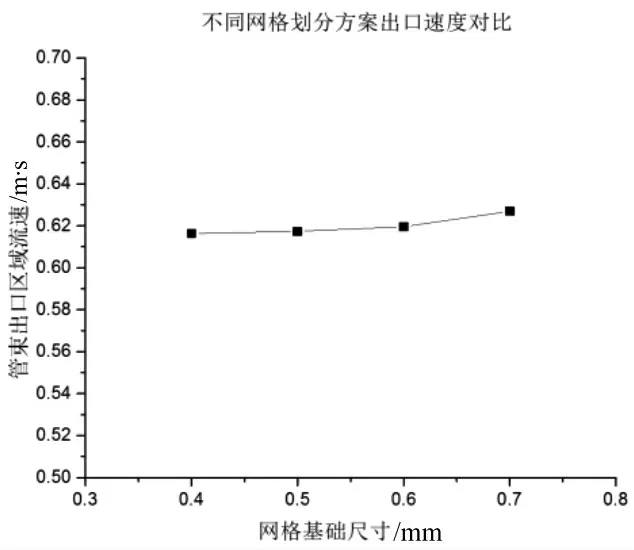
图2 网格划分方案的结果对比

图3 计算选取的网格模型

1.2 湍流模型的选取

数值计算选取的工况如表1 所示，其入口速度覆盖0.1～2 m/s。在该工况范围内，存在层流与湍流两类流动形式。因此，针对部分位于层流和湍流过渡区域的计算工况，分别采取层流模型和湍流模型同时开展计算，如果两种模型计算结果相差较大，在低条件下即选取层流模型计算结果，在高条件下选取湍流模型计算结果，作为最终结果进行分析。

表1 数值计算选用工况

本文湍流工况选取-ε 模型作为湍流模型，根据STAR-CCM+软件用户手册，-ε 模型适用于+∈（1，30）的计算工况。表2 给出了使用湍流模型的工况中的壁面+情况，表明使用-ε 湍流模型进行计算是合理的。

表2 湍流工况下壁面y+数值

基于工况Case 2-7，开展了层流模型与湍流模型下的数值计算，并提取了中心通道间隙处的平均速度，如表3 所示。对于入口速度=0.2 m/s、0.3 m/s、0.4 m/s 三种工况，中心通道棒间隙处的平均速度差值在=0.4 m/s 时最小，在入口速度=0.2 m/s 最大。当两种模型计算结果相差较大时，在低条件下，选取层流模型计算结果进行分析。对比两种模型计算结果，本文选取入口速度≤0.3 m/s 的工况，选用层流模型计算结果进行分析，而入口速度≥0.4 m/s 的工况，采用湍流模型计算结果进行分析。

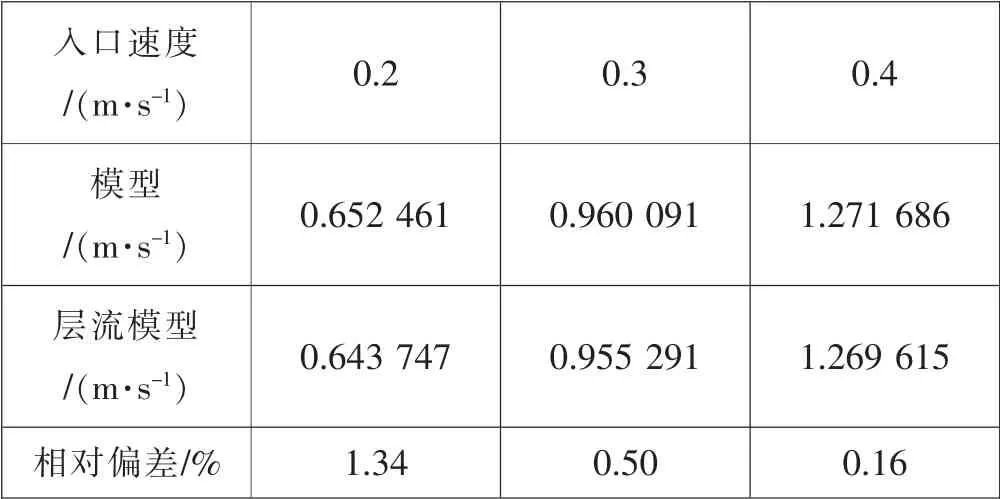
表3 层流与湍流模型的结果对比

2 数值计算结果分析

2.1 棒束通道横流流动特性分析

为更清晰地研究棒束区域内横流的流动规律，提取了棒束区域中心通道和边通道的中心线沿程的压力与速度分布，结果如图4 至图7 所示。

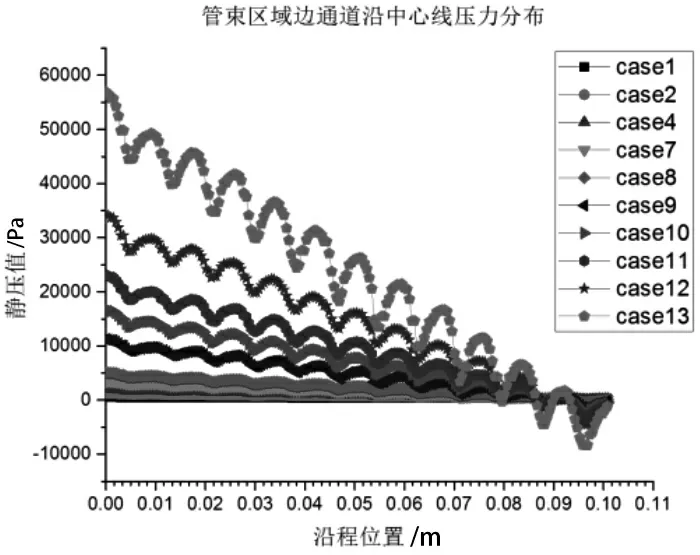
图7 棒束区域边通道沿中心线的压力分布

图4 至图5 给出了中心通道的速度压力分布特性，当横流初次进入棒束区域时，由于流动截面的减小，横流流速会不断增大，在棒间隙处达到最大。离开最窄间隙处后，由于流动截面积的增大，横流流速不断减小，子通道中心处达到最小。而中心通道沿程的压力分布显示，在子通道中心处压力数值最大，而棒间隙处压力数值最小。

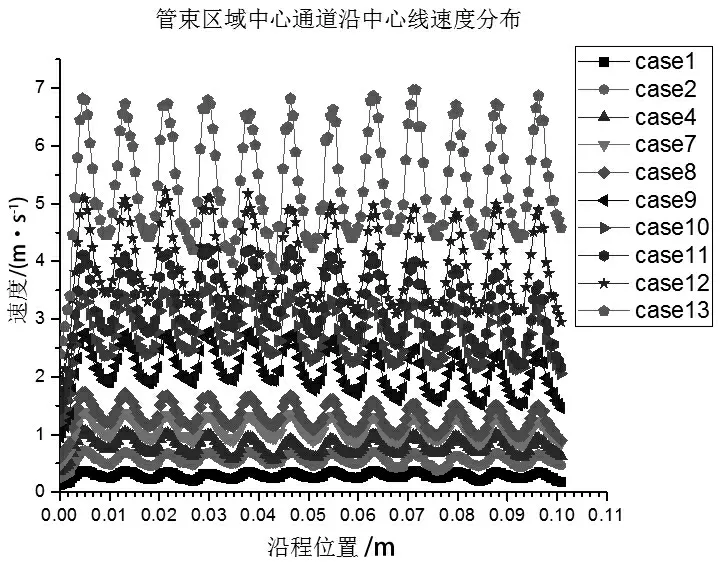
图4 棒束区域中心通道沿中心线的速度分布

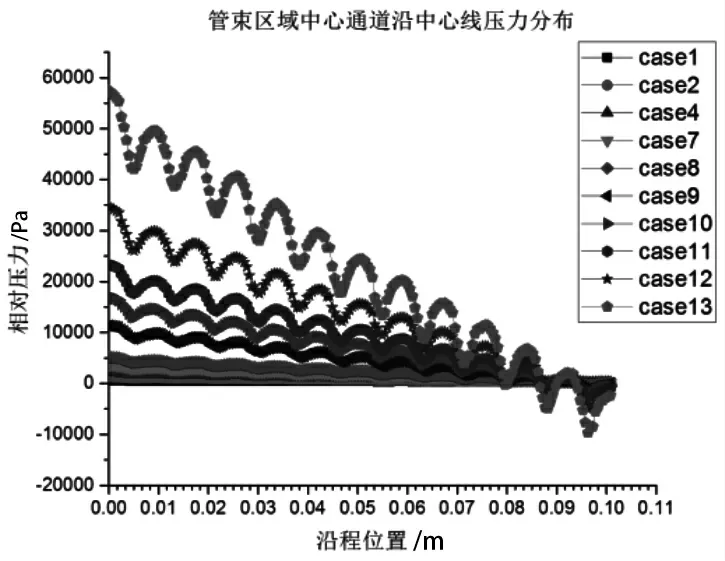
图5 棒束区域中心通道沿中心线的压力分布

与入口状态相比，进入棒束区域后，横流的速度会有明显提升，出现与通道结构相关的周期性振荡。而中心线上的压力分布显示，区域内横流出现了一定的压力损失，工况入口速度越高，在棒束区域内的压力损失越大。并且，计算结果显示，棒分布结构也会引起压力的周期性振荡，其振荡规律与速度相似，但其沿程的压力不断衰减。对于入口速度更大的横流工况，其在区域内的压力损失越大，速度的震荡幅值也越高。

中心通道与边通道内的横流速度与压力均会出现与棒束结构相关的振荡特性。而在两种类型通道内横流速度特性存在一定的差异。在棒束区域，中心通道的横流速度不断降低，而边通道横流速度整体呈升高趋势。导致两种通道内横流速度变化的主要原因是通道结构所引起的通道间扰流，中心通道的开式结构导致横流流动受到扰流影响，主流速度降低，边通道的半封闭结构会导致流动受扰流影响，速度不断升高。

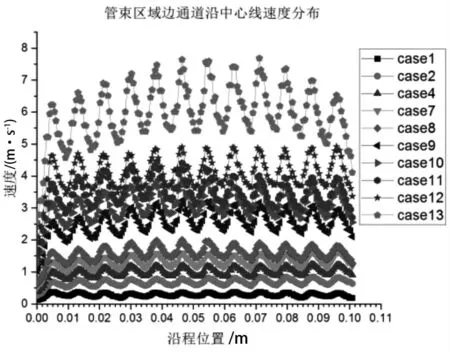
图6 棒束区域边通道沿中心线的速度分布

2.2 棒束区域横流阻力特性分析

为定量化研究棒束区域的阻力特性，使用无量纲阻力系数C，用于代表流动阻力特性。

式中，Δ为沿程的压力损失，ρ 为液体密度，为流体的速度幅值。

在廊道式棒束通道中，流体在经过棒束区域时，在棒间隙处由于流道截面的改变会出现压力数值的变化。同时，在棒束子通道中心，由于相邻通道间的交混，横向流动也会产生一定程度的扰流，影响沿程的压力分布。为得到更准确的棒束通道阻力系数的数值，本研究去除棒束入口以及出口区域结果，选用第2列以及第11 列棒间隙处的平均压力值计算总压力损失Δ，取10，并利用棒间隙处的平均速度，使用公式（2）计算通道内沿程的平均无量纲阻力系数C。

根据相似性原理，无量纲阻力系数为雷诺数的函数：

式中，为流体的密度，为流体的黏性系数，为棒束通道区域的入口速度，D为通道的特征长度，对于棒束区域的中心通道，选取间隙处的尺寸值，即D=3.1 mm；对于边通道，D=1.75 mm。

基于CFD 的计算结果，获得了阻力系数C与棒束入口雷诺数的变化趋势，如图8 所示。

图8 棒束通道内平均阻力系数随Re 变化趋势

从图8 可知，中心通道与边通道阻力系数随间隙处变化的趋势呈幂函数趋势衰减。在相同条件下，棒束中心通道的阻力系数要大于边通道，这意味着中心通道的压力损失要大于边通道。中心通道由于存在更多的相邻通道，因此子通道间的交混作用更强，这将引入更多的压力损失。

此外，根据CFD 计算结果，可以得到阻力系数与的拟合公式，其结果如图9、图10 所示。

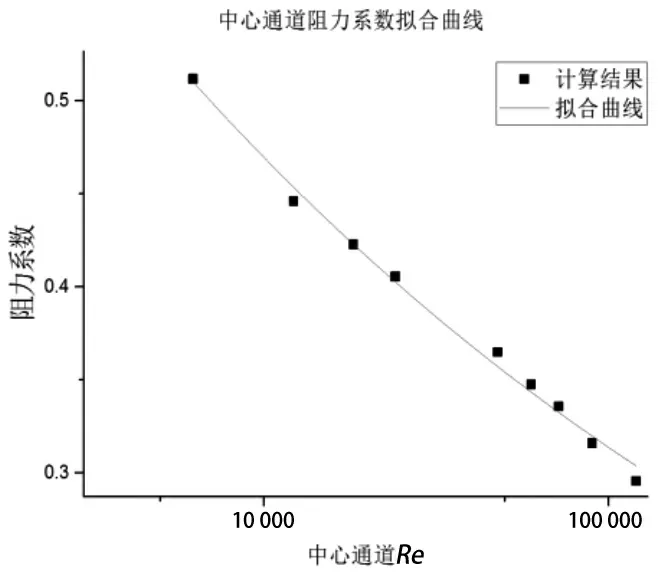
图9 中心通道阻力系数与Re 拟合曲线

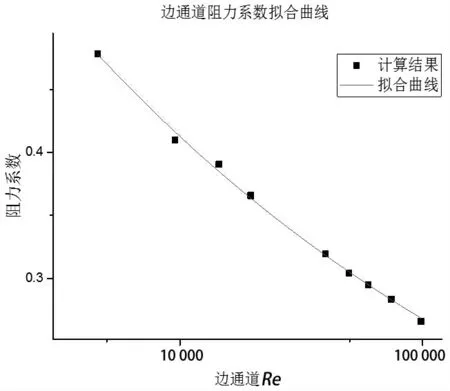
图10 边通道阻力系数与Re 拟合曲线

中心通道的阻力系数拟合公式为：

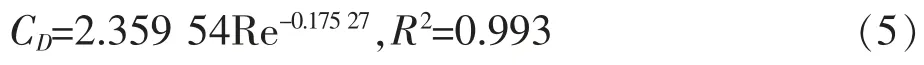
边通道的阻力系数拟合公式为：

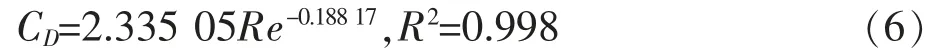
3 不同规模棒束通道横流流动特性差异分析

基于第1 节的计算方法，本研究改变棒束区域内列的数量，即在4×的棒束通道中，选取=4，=7，=10 三种规模的几何模型进行计算，结合第2 节的结果，研究列规模对棒束通道的影响。不同规模的棒束通道设为入口速度v=0.8 m/s。

图11 和图12 给出了棒束通道间隙处的平均速度以及棒束通道平均阻力系数与棒束列规模的关系。从图11 可以看出，随着棒束列规模的增加，边通道横流速度会增大，边通道横流速度会降低，这意味着棒束规模的增大使得不同通道间流体交混更加充分，从而促使中心通道速度不断降低，边通道速度不断增大。基于通道平均阻力系数可以发现，棒束列规模较小时，横流交混程度较低，从而导致流道截面积更小的边通道压力损失较小； 而当棒束列规模足够大时，横流交混程度较高，中心通道由于交混左右强于半封闭的边通道，沿主流方向的压力损失更大。

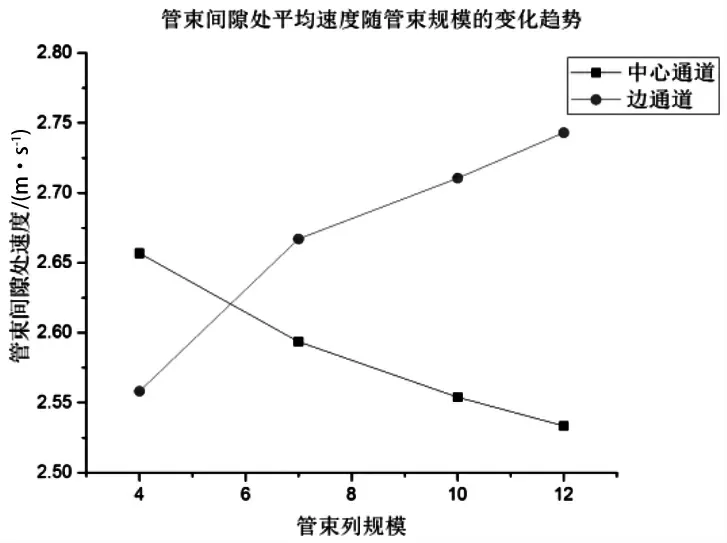
图11 不同棒束列规模的间隙平均速度

图12 不同棒束列规模的通道平均阻力系数

4 结语

本研究采用CFD 分析的方法，对棒束通道内的横流进行了数值研究。通过模拟，得到如下结论：

（1）分析了棒束中心通道与边通道内的横流流动特性，由于边通道的半封闭性，在交混作用下，中心通道的横流速度会不断降低，而边通道内的横流速度会不断升高。

（2）针对412 的棒束通道，提取出中心通道与边通道的平均阻力系数，并得到了阻力系数与Re 的拟合公式。

（3）对不同列规模的棒束通道，在入口速度较高的情形下，棒束规模越大，区域横流受到的交混作用越强，边通道内横流速度相对中心通道越高，压力损失越大。