基于熵权法构建真菌对木质纤维降解速率模型

黄怡嘉 吕祥旭 林佳伟

（江南大学物联网工程学院，江苏 无锡 214122）

0 引言

森林在调节气候、维持生态平衡和地球物质循环中的作用至关重要。森林凋落物的分解是驱动生物地球化学循环的重要过程，真菌是森林凋落物分解中最主要的微生物。在凋落物分解的不同阶段，参与的真菌种类也有不同；不同真菌对凋落物的分解速率受环境温湿度、土壤基质和养分等多种因素的影响。真菌群落还受气候、土壤、树种等因素影响。因此，森林凋落物分解是一个涉及多种因素的复杂问题。

鉴于碳、氮等物质循环在地球生物化学循环中的重要性，准确估算凋落物分解速率对于地球物质循环研究有重要意义。然而，凋落物分解试验受时间和环境条件等多因素的限制，一般都以小规模试验为主。早期研究者以凋落物的失重率来描述，后来开始用数学建模的方式进行研究，从简单的线性模型发展到后来的单指数模型、 双指数或三指数模型等。Lustenhouwer 等在PNAS 上发表了对34 种腐生真菌降解木质纤维做的长达五年的研究，结果发现真菌生长速率、耐湿性等特性对木质纤维分解速率有着极为重要的影响。2021 年2 月美国大学生数学建模竞赛（Mathematical Contest In Modeling，MCM）A 题基于此研究成果建模，笔者有幸参加并获得了Honorable Mention 奖（二等奖），现将建模思路和过程报道如下，以供参考。

1 真菌群落分解水平评价模型的建立

基于Lustenhouwer 等的成果，选取真菌生长速率、 耐湿性两个重要特性作为参考因素，用熵权法（Entropy weight method，EWM）建立总归因指标（Total attribution index，）来衡量真菌群落的分解水平，再用分位图法检验与参考因素之间的相关性，最终通过Sobol 法检验模型的可靠性。

在信息论中，熵可以用来度量某一状态数据的有效信息量，熵权表示项目因素在系统中的权重。影响森林凋落物分解的因素有很多，以凋落物的分解速率为总归因指标，采用熵权法对影响因素分别赋权，来衡量真菌对纤维木质的分解水平。由于不同真菌种类对木质纤维的分解能力有差异，用目标差异（Goal difference，）来描述真菌种类的分解效果差异，用目标方差来衡量真菌种类的实际分解效果。最后，分析总归因指标与实际分解效果之间的相关性。基于文献[1]的真菌分解木质纤维的研究报告及数据，选择了湿度生态位宽度（以下简称耐湿性）、群落间竞争、真菌生长速率和木块腐朽时间共4 个因素来评价木质纤维的分解速率。先分别将以上4 个因子定义为、、和，使用熵权法，经数据标准化、求熵值，计算4个因素的权重，再对这些因素进行加权，得到总归因指标计算公式：

2 真菌特性相关性与模型的求解

为了了解群落实际分解目标差异（）与得到的总归因指标（）之间是否存在相关关系，使用分位图（Quantile-Quantile）对它们进行分析，结果如图1 所示。

图1 目标差异（GD）与总归因指标（TAI）的分位图

从图可知，二者呈显著的正相关（=0.927），拟合方程为=2.059+0.659。说明获得的总归因指标能够反映木质纤维凋落物的分解速率，分解速率与菌丝延伸率和耐湿性这两个性状高度相关。

为了模拟真菌生长速率、菌丝耐湿性与木质降解速率之间的数学关系，从参考文献[1]中的Figure1 和Figure2 中提取出与菌丝延伸速率有关的降解速率（Decomposition Rate Relating to hyphae extension rate）和菌丝延伸率（Hyphal Extension Rate）、与菌丝湿度耐受有关的降解速率（Decomposition Rate Relating to moisture tolerance） 和耐湿性（Moisture Tolerance）的数据用于建模。然后，利用k-最近邻算法（K-Nearest Neighbor，KNN）计算（设为）和（设为）之间的曼哈顿距离（Manhattan Distance）（，）。当（，）取得最小值时：

由于不同温度下（10℃、16℃、22℃）真菌对木质纤维的降解速率不同，基于熵权法使用MATLAB 计算了在不同温度下和的权重：

=10℃∶=0.409 2∶0.590 8

=16℃∶=0.278 7∶0.721 3

=22℃∶=0.407 0∶0.593 0

由于温度不是与关系中的变量，所以分别求和在3 个不同温度下的算术平均值来代表一般温度情况下和的平均权重：

则总分解速率（Total decomposition rate，TDR）为：

为了进一步获得与真菌生长速率、 耐湿性的数据关系，进一步求出了和与、的数据关系。即根据参考文献[1]中Figure 1 的数据，利用MATLAB 绘制出与的关系图，如图2 所示，获得的拟合曲线方程如式（5）所示：

同样，利用MATLAB 对和绘制散点图和拟合曲线（见图2）：

图2 总分解速率（TDR）与菌丝湿度耐受性（R1）和真菌生长速率（R3）的拟合曲线

将模型中和两个因素结合后，最终获得以真菌生长速率、 耐湿性为主要因子的木质纤维分解模型：

3 模型的灵敏度检验

由于真菌生长速率和竞争能力受环境条件的影响，基于种群竞争模型中建立的真菌生长速率和耐湿性对总分解速率的敏感性，计算出不同种类真菌的平均耐湿性为0.103 5±0.480 5（均数±标准差），真菌生长速率的平均值为1.758 4±1.618 8（mm·day）。接着，利用Sobol 法检验的灵敏度。首先，将耐湿性（）设定在平均值上，对菌丝延伸率进行波动，经过数据处理，得到的取值范围：[4.696 9，21.192 3]，90%和95%的置信区间如图3 所示；同法，菌丝伸长率（R3）在90%和95%的置信区间分别为[8.386 7，11.152 2]和[8.308 2，11.227 3]，无论是菌丝伸长率还是耐湿性的波动区间均在合理范围内，与Lustenhouwer 等的实测数据区间相符，模型行为模式没有因参数的微小变动而出现异动，表明模型可信。

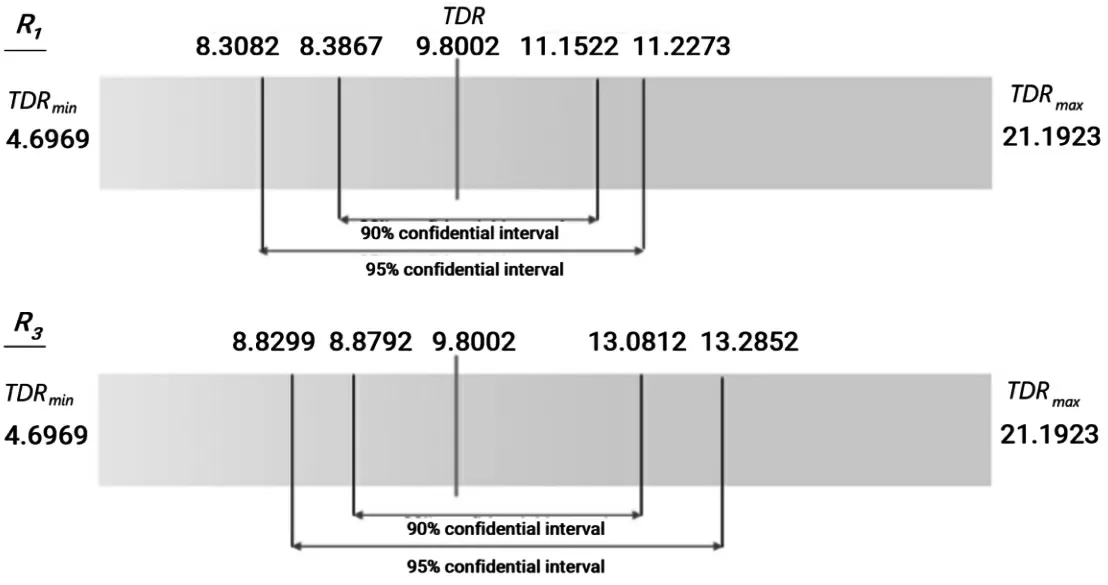
图3 耐湿性（R1）和真菌生长速率（R3）波动时总分解速率（TDR）的置信区间

4 结语

碳循环作为生态系统不可或缺的重要组成部分，植物材料和木质纤维的分解在其中有举足轻重的贡献，而这些材料的分解主要依靠着真菌。本文通过对文献[1]数据的分析，采用数学建模的方法模拟了真菌对木质纤维分解速率，并结合熵权法进行求解，得到了耐湿性与真菌生长速率的定量关系模型，具有较高的可靠性，是用熵权法建模以评估真菌群落分解木质纤维速率的一个有意义的尝试。从建模角度而言，一方面要尽可能覆盖不同环境，包含所有的主要影响因素，才可能使模型更具有普适性；另一方面又要防止因素过多使模型过于复杂而降低外推的实用性。当然，真实的木质分解过程受到气候环境、土壤环境、真菌群落等多种因素的影响，是一个相当复杂的过程。该模型的推广与延伸还需要获取其他森林环境下更多数据进行测试和改进优化，才能更好适用性的模型。