惯性导航传感器环形陀螺仪的正交误差仿真分析
2022-05-20丁徐锴
张 含,李 昂,2,丁徐锴
(1.南京理工大学紫金学院,江苏 南京 210023;2.南京邮电大学 通信学院,江苏 南京 210003;3.东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引 言
物联网技术的发展使信息化和智能化的硕果惠及千家万户,尤其是定位导航技术,大大满足了人类对位置信息的服务需求,真正实现了人与万物互联。2020年6月23日,随着北斗三号最后一颗组网卫星成功发射,我国自主研制的卫星导航系统也开始投入使用。但目前卫星导航技术的局限在于受应用场景的影响较大,如建筑物内部磁失真严重,会导致卫星导航技术应用于室内环境时精度较差。作为北斗导航产业的战略补充,各种基于室内导航的技术及算法应运而生。目前较为成熟的定位技术主要有基于无线信号交汇的定位定向技术、基于数据库的匹配定位技术、基于惯性传感器的航迹推算技术以及基于信息融合的组合定位定向技术。随着微型化和集成化工艺的发展,基于MEMS陀螺仪传感信号的惯性导航设备可佩戴性好、短期精度更高、成本和功耗也更具优势,使之成为了室内导航技术方式的热门之选。
传感部件是惯性导航系统的核心,其中环形陀螺仪凭借其可以直接测量角度得到姿控信息的功能,避免了后续积分电路误差的产生,成为高精度惯性导航家族中的领军者,但囿于目前加工工艺和封装水平,环形谐振子两个工作模态会相互耦合产生正交误差,恶化陀螺仪角度输出精度,因此减小正交误差是提高惯性导航定位精度的关键所在。负刚度效应是改善陀螺仪传感器正交误差的一项经典理论,即利用正交校正电极上的外部电压改变谐振子刚度,以此实现0°和45°电极方向的运动解耦。目前针对这一理论研究成果更多的是理论公式直接凌驾于实际外围电路所得到的控制方法,谐振子的结构参数变化过程依旧是一个黑匣子,因此本文提出一种基于COMSOL Multiphysics仿真平台设计出的谐振子结构模型,观察校正电极上的电压变化如何影响谐振子的刚度、模态角度、模态频率等参数,为进一步构思提高定位导航精度方案奠定理论基础。
1 环形陀螺仪电极的基本配置
环形陀螺仪的传感器结构主要包含谐振子、电极和基座,谐振子有两个工作模态,分别为sin和cos模态;其导航定位原理主要基于两个模态的能量传递,在cos模态的激励电极加载电压,当有外界角速度输入时,环形谐振子会发生驻波进动,进动后的振型可由两个工作模态叠加表示,利用sin模态读出电极得到的数据即可反映角度信息。谐振子电极的一般配置如图1所示。
图1 环形谐振子电极配置
1.1 环形谐振子误差模型
理想的环形谐振子主要具有以下特征:(1)cos和sin两个工作模态参数完全对称;(2)两个模态相互独立,无正交耦合误差;(3)模态主轴方位角θ方向任意,唯两个模态的方位角差值大小恒保持45°不变。而由于陀螺仪的制备材料单晶硅具有各向异性和加工误差,实际加工出来的环形陀螺仪常常存在模态失配,导致正交耦合和方位角误差的出现。为了改善精度,需要在谐振子上嵌入正交控制电极,利用静电负刚度原理,在控制电极加载直流电压,解耦两个工作模态,消除正交误差。如图1所示,设正交控制电极I组上施加的直流电压为,II组上施加的直流电压为,基于负刚度原理,这两组电极引入的静电刚度矩阵K为:


图2 负刚度校正电压加载示意图
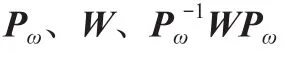
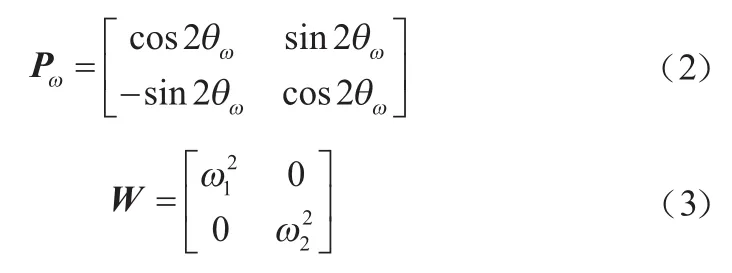
令:

其中:
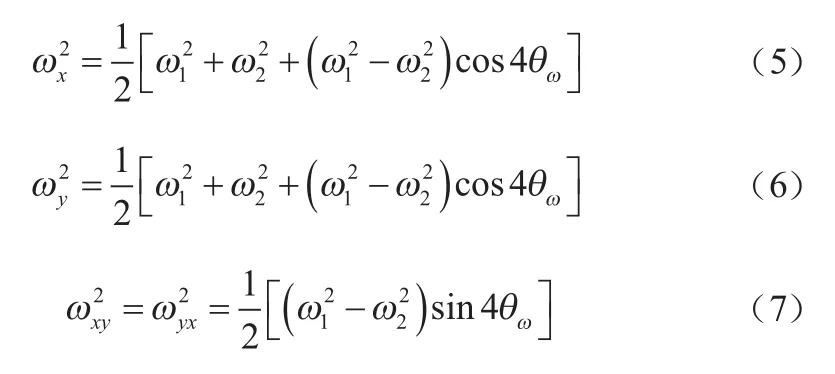
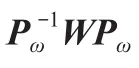
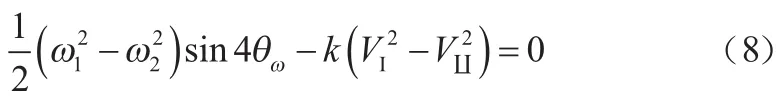
通常为了提高校正效率,校正电极I组和II组只选用其中一组即可。如图2(a)所示,图中表示电极上所施加的电压,若环形谐振子频率较高的模态主轴落在0~45°之间时,可令II组电极电压为零;当I组电极电压从零慢慢增大时,模态主轴方位角会慢慢减小,逐渐靠近0°电极方向;当调节至满足式(7)的方位角关系时,则耦合完全消失,模态主轴与电极轴正好对准,如图2(b)所示。若高频率主轴落在-45~0°之间,则电压配置相反。
1.2 环形谐振子结构尺寸
图3所示为轴向、弧长为的读出电极环形谐振子示意图。当<<时,读出电极在处、d微元角度范围内的电容量可表示为:
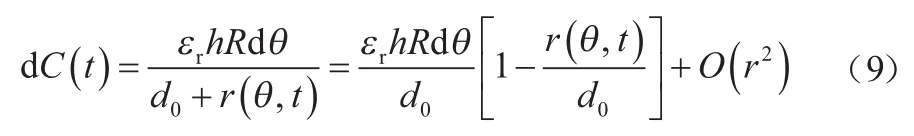
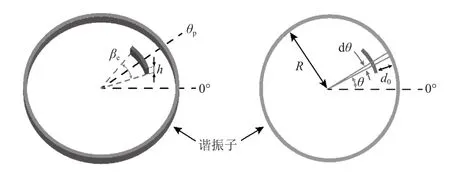
图3 环形谐振子与读出电极位置示意图
其中,是介电常数。将式(9)的 电容量在 [-/2,+/2]的范围进行角度微元积分,得到总电容量为:
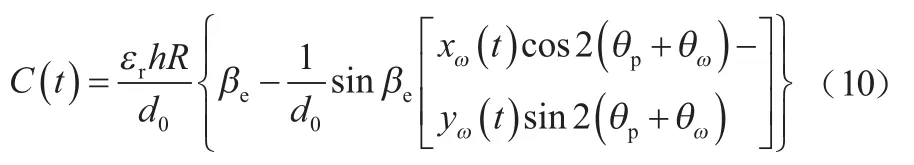
当陀螺仪有外界角速度输入时,谐振子的外嵌电极发生位移,导致极板间电容量改变,通过后续的电容-电压转换电路将运动信息反映出来,达到导航和定位的目的。
为了验证式(8)中直流校正电压与主轴方位角θ的关系,并研究正交误差校正过程中各个参数的变化趋势,考虑到惯性传感器整体尺寸处于毫米级,难以直接测量获取结构参数信息,本文基于有限元仿真平台COMSOL Multiphysics,建立谐振子结构的3D仿真模型。
2 环形谐振子仿真建模
环形谐振子主要由环形结构和支撑梁构成,环结构外围一周均匀分布着两个工作模态的激励、读出及正交控制电极,如图1所示。建模时须同时设置弹性结构体和电气结构体。由于谐振子的制备材料是硅,因此将环结构和支撑梁设置为弹性导体,将环结构与电极之间的介质设置成厚度为的空气介质,另外将电容极板与介质的接触位置设置为“机电接口”,在电容介质最外边缘添加电势约束,作为外部加载电压。根据表1谐振子实际尺寸设计模型的仿真参数;谐振子的加工误差可以通过外加一个质量扰动来模拟,扰动坐标为cos(±),为方便分析,令=30°,即非理想谐振子的主轴方位角偏向30°方向。考虑到电极运动幅度极小,因此可忽略电极本身的几何模型,然后将电容介质与弹性结构体两者的接触面设置为“机电接口”,如图4所示。

表1 环形谐振子结构尺寸

图4 机电几何模型
有限元仿真计算时,网格分辨率的大小决定了仿真结果的精度和运算周期的长短。分辨率低,计算时间短,但可能导致与实际结果情况存在较大偏差;而过高的分辨率则要以牺牲计算时间为代价。COMSOL Multiphysics提供了9种网格划分尺寸,除默认“常规尺寸”外,按照网格尺寸从大到小,将“极粗”到“极细”的范围另细分出8个级别。本文的仿真对象为环形谐振子,整体尺寸介于数个毫米单位之间,电极间距介于数个微米单位之间。结合这两种不同量级的尺寸,本文将结构体分成三个部分:电容介质部分、环形极板、支撑梁和锚点。针对这三个组成部分,设置三种网格划分标准,电容介质部分预置为“最密”,环形极板预置为“较密”,其余结构体预置为“较粗”,如图5所示。

图5 环形谐振子有限元网格仿真模型
3 仿真模型和静电刚度校正实验验证
3.1 仿真模型验证
根据前文分析,现仿真结构中频率较高的模态主轴方位角为30°,落在22.5~45°区间内,因此在位于22.5°方向的正交电极I组上施加校正电压,此时模态频率较高的主轴会向45°轴向偏移。其中,当校正电压为15 V时,模态主轴大致偏向45.4°;再增大电压时,模态轴向会继续逆时针旋转,出现过校正状态;当电压达到20 V时,高频率主轴方位角为55.7°。由于一般主轴方位角的定义范围是-45~45°,因此该方位角应视为-34.3°,如图6所示。
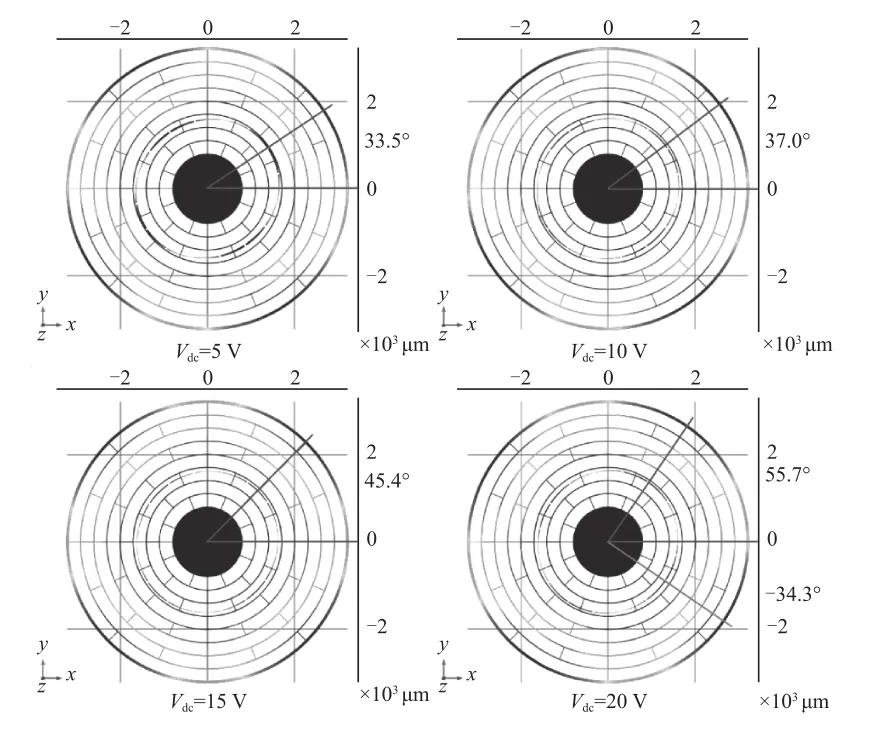
图6 不同校正电压下的高频率模态主轴方位角
根据前文设置的模态主轴方位角(30°方向),在第一组校正电极(22.5°方向)开始校正,利用有限元仿真的参数扫描功能,分别改变两个模态电压的幅度,观察主轴方位角的变化趋势,并将两个变量数据进行拟合,拟合曲线如图7所示。观察图7曲线,当电压达到15 V时,cos和sin两个模态的方位角差值接近45°,说明正交耦合误差基本消除。
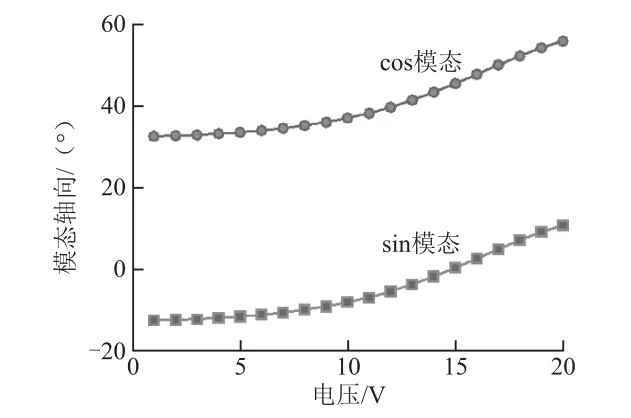
图7 校正电压-模态主轴方位角关系曲线
随着校正电压的增大,两个模态的主轴方位角与电压近似成线性关系变化,与式(8)中θ-的函数关系一致,证明本文设计的仿真模型符合理论结果。
3.2 静电刚度校正实验
针对上述有限元仿真模型的建立,利用真实环形陀螺仪进行实验验证,陀螺仪样机如图8所示。

图8 测试所用的环形陀螺仪样机
通过图9中的示波器波形可知环形传感器在正交电极控制下的误差信号变化趋势,当没有加载校正直流电压,即=0 V时,正交误差信号的幅度为3.04 V,该误差信号幅度较大,会影响被测信号,因此需要校正;随着校正电压的增大,正交误差信号逐渐减小;当校正电压加载到15 V以上时,误差信号峰峰值为9.7 mV,基本可以忽略不计,所测试的谐振子完成了正交校正,与模型仿真结果一致。

图9 环形陀螺仪负刚度实验
4 结 语
本文针对惯性导航传感器环形陀螺仪因正交误差造成的定位精度问题,基于静电负刚度校正原理,利用COMSOL Multiphysics仿真软件设计出环形传感器的结构模型,并验证出模态主轴方位角与外部施加电压的关系,不仅减小了仿真计算周期,同时打破以往误差校正过程中传感器结构参数不透明的技术壁垒,可以为高精度传感器结构设计提供参考。
