指向认知冲突的小学数学深度学习教学策略研究

陈璐

在小学数学的实际教学中，我们经常发现课堂上一些新知识或重难点存在学生接受困难、难以内化的情况，导致课堂练习做得也不理想。从表面来看，这些知识点或难度较高，或容易让学生混淆，但究其根本是学生对这些新概念的理解不够透彻，没有进入深度学习导致的。

新知识的学习过程其实是一个冲突形成、化解并且發展的过程。在学习新知前，学生的原有认知处于平衡状态，而当遇到与已有经验不符的结论时，平衡就会被打破，认知结构被更新，并再次达到平衡。正是在一次次的“平衡—不平衡—再平衡”的闭环链中，学生收获了新知识。而很多教学并没有基于这样的闭环进行设计，致使学生学习效果难达预期。尤其是在现如今的“双减”背景下，教师若没有适时创设冲突、及时化解认知冲突，学生精力就会浪费在课下题目的纠错订正上，陷入学习困境。教师若能基于认知冲突设计教学，就可帮助学生打破认知局限、建构新的知识网络，帮助学生高效理解新知识，掌握系统性学习方法，为后续学习打下坚实的基础，对减轻学生课业负担大有裨益。

一、运用思维定式创设认知冲突情境

小学是数学学习的筑基时期，学生尚未形成完善的数学思维。这导致在学习新知识时，学生往往会从过去的思维定式和已有的思维规律出发。当我们通过认知冲突打破学生原有的思维定式时，学生追究事物缘由的热情会就被“点燃”，内驱力、质疑能力等深度学习素养同时也被激发出来。

（一）基于学生已有认知基础创设冲突问题真实情境

美国著名教育家奥苏伯尔认为：“影响学习的最重要的因素，就是学生已经知道了什么。”现代教学应当更注重研究学生。所以教师在创设冲突问题情境时，要充分了解学生认知水平和生活经验，进而设计合理有效的认知冲突，帮助学生打破思维惯性，使每位学生亲身经历新知识的发生和发展，领悟所学知识的核心内涵。

在沪教版四上《容积和体积》的教学前，教师通过访谈法进行学生调研。随机调查几名学生问：“什么是体积？”有的同学认为矿泉水瓶上标注的500 mL就是体积，有的同学认为质量重的物体体积大，还有的同学说不清……因此，教师发现，学生对容积和体积的概念两者混淆不清，并且还存在“质量越重体积越大”这样的认知误区。于是教师利用学生原有的错误认知，设计了一个这样的体验式教学活动：请学生到讲台前，用布遮住眼睛，准备一块砖头和塑料泡沫箱，用绳子分别挂到学生的手臂上，让学生猜猜哪个体积大。学生猜砖头体积大。当学生看到是泡沫箱体积更大时，会形成非常强烈的认知冲突：“重的东西怎么体积反而小呢？”学生原有的思维定式被打破，形成新的认知：原来体积和质量没有关系。

“质量大的物体体积越大”是学生受原有生活经验的影响形成的思维定式。如果教师利用传统的讲授法直接告诉学生“重的物体不一定体积大”，可能强调很多遍学生也记不住，所以教师的高明之处不是直接告诉，而是基于学生已有的认知基础，抓住学生的认知难点，创设真实的问题情境，引导学生在原有的认知经验和新知识间形成强烈的冲突，从而让学生深刻体验，深度学习也随之发生。

（二）强调学生学习情绪动力创设认知冲突破解契机

传统的“填鸭式”教学是单一方向的知识传递，学生被动接受知识，难以产生学习兴趣，甚至会丧失主动学习的欲望。而巧用认知冲突，则可以显著调动学生的主观能动性。在认知冲突的创设和破解过程中，学生发现已有经验无法解决新问题时，学习情绪一定趋于高涨，思维亢奋，学生的好奇心和求知欲得以激发。同时，在教学中设置真实有效的认知冲突，还能够唤起学生的思维注意，触及学生内心情感，充分调动学生情绪，使学生从心理情绪上深度参与到课堂教学中。

在沪教版三年级下《几分之一》的教学时，教师创设了一个生活情境：今天是小胖的生日，小丁丁为他庆祝，两人准备平分零食，有16块巧克力，8颗糖果，还有2个苹果和一个生日蛋糕，应该怎么分呢？对于巧克力、糖果、苹果这些零食，可以利用除法算式平均分成两份：16÷2=8（块）、8÷2=4（颗）、2÷2=1（个），但平分一个生日蛋糕的算式则是“1÷2”，学生无法计算得出具体的运算结果。有的学生回答：“一人一半。”此时教师追问：“一半可以用我们以前学过的数表示吗？”引发学生认知冲突，激发学生兴趣，于是教师揭示课题：“生活中我们经常遇到连1个都分不到的情况，所以需要来认识一种新的数——分数。”

几分之一是分数学习的开端，从整数到分数是数字概念的一次大维度拓展，是学生认识数的概念的一次思维跃迁。所以从整数到分数也是学生认知上的一次突破，学生利用整数的学习经验无法解决“一半”的问题时，他们的认知平衡被打破，同时内驱力被激发并萌发出强烈的求知欲，他们会更积极主动地投入下阶段的分数学习中去，这也为破解转化认知冲突提供了契机。

二、巧设探究活动激发认知冲突矛盾

（一）设计差异性实验挖掘学生隐藏的错误认知经验

美国著名教育学家杜威强调“做中学”。数学课程标准也提倡学生在学习活动中去动手操作，去经历体验整个过程，从而获得知识，深刻理解概念的实质。因此，教师在实际教学中可以基于小学生的年龄特征和特殊的心理状态，通过探究、动手实验等形式，建立认知冲突，打破具象化，更高效地纠正、升级学生的认知体系。

在沪教版三上《面积》教学时，教师设计了以下四个不同层次的学生实验活动。第一层次利用观察法比较数学书和黑板的面积。第二层次利用重叠法比较两个宽相同的长方形的面积。第三层次比较一个正方形（4 cm×4 cm）和长方形（5 cm×3 cm）异类形状图形的面积。在第三次比较时，学生首先想到了重叠法，但重叠后学生无法比较出大小，出现了认知冲突，此时教师为学生提供了不同的差异性学具：尺子、直径为1 cm的小正方形和直径为1 cm的小圆形纸片，让学生在动手操作中比较，再一次挖掘学生的认知冲突：为什么不用尺？为什么用正方形纸片而不用圆形纸片？从而得到用正方形表示面积单位的过程。此时学生的认知达到了又一次的平衡，教师又设计了第四次差异性实验游戏：请女生闭眼，男生观察图1中图形占几格。再请男生闭眼，女生观察图2中图形占几格。此时同时呈现两张图片，于是再一次引发认知冲突：为什么同样是15格，却不一样大？从而让学生真切地认识到测量或比较面积时采用统一单位的必要性。

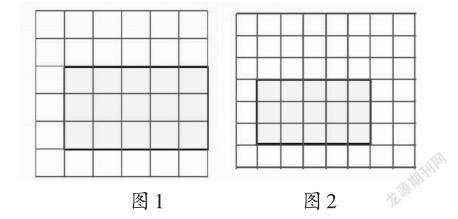
面积属于概念领域，教学的关键在于感受建立面积单位概念的必要性。小学生的思维偏向具象化，于是教师利用四次不同层面的实验活动，利用差异性直观的学具，层层递进，逐步挖掘学生隐藏的错误认知经验，逐渐让课堂教学达到高潮。学生在观察、操作、比较中，全身心地参与体验实验过程，经历知识的形成，达到深度学习的目的。

（二）充分合作式学习放大学生对话中的矛盾认知经验

知识可以分为两类，一种是世界的客观规律，另一种则是社会共识。后者具有典型的社会性特征，它们大多是人与人围绕特定问题沟通、互认的结果。而在数学中，就有很多概念是建立在社会共识、互认的基础之上。对这种社会性知识，我们可以设计合作式学习来帮助学生摆脱自我认知的局限性。所以，在教学设计中要设疑争辩，让学生在沟通、合作、参与社会性讨论的过程中放大对话中的矛盾认知，使不同的思维相互碰撞。这一过程伴随着认知冲突的激发和破解，可以促使学生打破思维茧房，实现认知升级和思维破局。

在学习“三角形（按角）分类”时，教师利用信封遮挡住三角形的一部分（如图3、4、5所示），只露出一个角，多媒体依次出示，教师同时提问：“你能判断出信封下面是什么三角形吗？”对于图3、图4，学生能快速做出正确判断，二者分别是直角三角形和钝角三角形。但当出示图5时，学生冲突四起，有人坚信是锐角三角形，有人认为也可能是直角三角形，有人则判断为钝角三角形，还有的认为三种都有可能。于是教师让学生合作交流，展开激烈的讨论对话。当小组合作结束时，在头脑风暴中有些学生已经改变原有的观点，被学习小伙伴说服，认为三种三角形都有可能。于是教师拿走信封揭晓答案，学生也重新建构了自己的观点：有一个锐角的三角形不一定是锐角三角形，只有三个都是锐角的三角形才是锐角三角形。

在锐角三角形、钝角三角形和直角三角形的概念学习后，由于受“钝角三角形和直角三角形”判定的标准的限制，学生容易产生思维定式，对锐角三角形的判定标准建构不扎实，观点不够清晰。此时教师利用学生的合作式学习，在彼此争辩中放大学生的矛盾认知经验，学生在对话过程中，由于他人观点的介入，会让自己的思维得到拓展，进而重新审视自己的观点。让学生认识到任何类型的三角形都有锐角存在，不能只依靠一个锐角去判断是什么三角形，从而突破了难点。

三、聚焦类比迁移搭建认知冲突破解支架

（一）注重规律探索在非规律不吻合处化解认知冲突

从旧知到新知的冲突破解一般有两种结果：一种是学生旧知正确，能够正向迁移到新的认知体系中，思维模型可以顺利地得到完善。另一种则相反，原有认知错误或与新知识有冲突、不吻合，若负向迁移到新知识上，会大大影响学习的效果。因此，在新旧交替迁移的过程中，教学设计要着重关注新规律的探索和修正，及时并彻底地引导学生化解新旧之间的非规律、不吻合等冲突，为学生搭建起正确的迁移学习支架，顺利实现破旧立新。

在学习乘法交换律、乘法结合律和乘法分配律后，学生去做这样一道题目：8×（12×125），不少同学会出现这样的答案：

8×（12×125）=（8×12）×（8×125）=96×1 000=96 000

学生误以为自己成功运用了乘法分配律。此时教师可以将正确运算过程呈现出来，形成对比，让学生寻异辨法：乘法交换律和乘法结合律只有乘法运算，而乘法分配律是乘、加（乘、减）两种运算之间的规律（如表1所示）。于是学生理解了乘法结合律的运算规律。

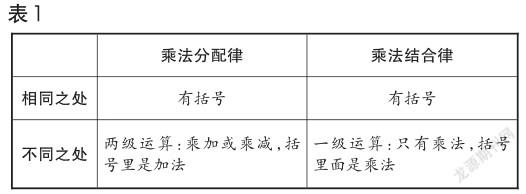
学生受加法结合律、加法交换律、乘法交换律、乘法结合律学习的经验影响，认为乘法分配律中也只有乘法，所以在字面理解上的矛盾冲突造成了知识负迁移。教师利用对比，注重规律的探索，让学生深刻理解两个运算规律的区别和联系，从而化解了认知冲突。

（二）借助变式训练在新旧知识衔接处化解认知冲突

数学学习不是简单的模仿，学生在新认知成功建构的初期，思维体系尚处于不稳固状态，学生在自己解决问题时，仍有较大概率会回归到原有的旧认知上。因此在实际教学中，教师有必要通过变换实例中的条件和形式，在层层递进的变式训练中创设认知冲突，为学生渗透新的思想方法，形成举一反三、融会贯通的能力，更加牢固地掌握概念的本质。

在沪教版《倍》的教学中，学习完“倍”的概念后，教师可以设计以下两个变式。变式1：比较量不变，倍数变。第二行给出8个△，请你在第一行画○，并根据它们的个数关系填空。呈现资源，并提问：为什么你们的倍数不一样呢？教师总结：原来1份的量发生了变化，倍数关系也会随之发生变化。

变式2：倍数不变，一倍量和几倍量同时变。要求：拿出小圆片摆一摆，第一行摆蓝色小圆片，第二行摆红色小圆片。红色圆片的个数是蓝色圆片的3倍。呈现资源，并提问：要求是一样的，为什么你们用的小圆片的个数不一样呢？教师总结：因为一份数不同所以倍数不同。只要第一行确定了，第二行就摆这样的3份，所以说找准一份的数量很重要！

在日常生活中学生对“倍”的概念接触得比较少，对倍的认知比较模糊。所以教师可利用变换实例，不改变题目的本质属性，让学生深入理解“倍”的概念：倍是一个量相当于几个另一个量。在变式一和变式二中，创设两次认知冲突：“为什么△个数不变，倍数却在变呢？”“為什么同样是3倍，而你们用的小圆片的个数却不一样呢？”学生利用前面积累的学习经验，类比迁移到新例子中，在对比观察中学生主动思考“变与不变”的奥秘，化解了认知冲突，进一步认识倍的概念，体会倍数关系。

总之，基于认知冲突的教学设计，可以更加有效地引导学生找到新旧知识的矛盾点、新知识的生长点，以及解决问题的关键点，充分调动学生的内驱力，促进学生主动建构。在此过程中，教学设计可以巧妙借助动手操作、合作争辩，帮助学生实现解构、重构思维模型。最后教师要善于捕捉学生的易错点，运用类比迁移、变式训练化解认知冲突，进一步深化新知识的理解，在持续活跃的思维状态中落实深度学习。