含有定积分的数列极限的计算方法研究*

庄科俊

(安徽财经大学统计与应用数学学院，安徽 蚌埠 233041)

引言

数列极限是数学分析或高等数学中的重要内容，关于各种类型数列的收敛性判别与极限计算，对初学者来说，有一定的难度. 在一些经典教材的基础上，已有研究者对常见数列极限的计算方法进行了总结与深化[1-3]. 然而，如果数列极限中含有定积分，特别是积分限含有数列变量时，常规的计算方法往往失效，通常无法先求定积分再计算极限，也很少满足交换运算次序的条件或者交换运算次序后仍然很难求解，这就需要综合运用定积分的各种性质和运算法则进行分析，难度较大. 而这类问题在全国大学生数学竞赛和研究生入学考试专业课试题中又经常出现， 因此，有研究者通过具体例子，对一些积分极限进行了深入的分析和研究[4-8]. 然而，对含有定积分的数列极限还远不止于此，仍有待进一步的研究.

因此，本文将利用积分中值定理、迫敛性、拟合法与数列极限定义等，给出求解此类特殊极限的几种常用方法，并通过具体例题进行分析和说明，进而推广已有文献的结果.

为了方便，下面给出定积分的中值定理和迫敛性结论[9].

定理1(积分第一中值定理) 若f在[a,b]上连续，则至少存在一点ξ∈(a,b)，使得

注 当g(x)=1时，即为定理1.

定理3(积分第二中值定理) 设函数f(x)在[a,b]上可积，

1)若函数g(x)在[a,b]上减，且g(x)≥0，则存在ξ∈[a,b]，使得

2)若函数g(x)在[a,b]上增，且g(x)≥0，则存在η∈[a,b]，使得

3)若函数g(x)在[a,b]单调，则存在ξ∈[a,b]，使得

1 利用积分中值定理求极限

(2) 由f(x)在[0,1]上连续，故有界. 根据推广的积分第一中值定理，存在ξ∈(0,1)，使得

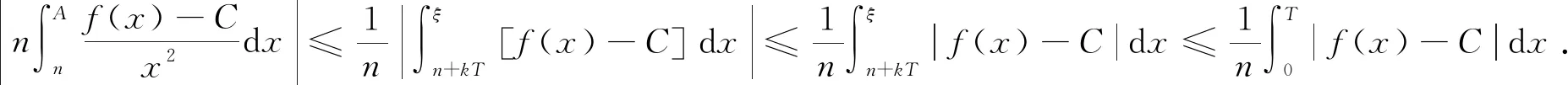
2 利用迫敛性求极限

对于数列变量n仅出现在被积函数中的情形，也可结合积分计算方法、积分估值定理等先对积分进行估计，再利用迫敛性进行计算.

注：本例不同于文献[6]中的例5，这里的条件较弱，f(x)仅仅可积而非连续，所以处理细节有所不同.

解 利用定积分的分部积分法，可得

注 本例也是文献[7]中的例1、文献[8]中的例3的特殊情形，取f(x)=ex即得.

3 利用拟合法求极限

注 本例也可利用推广的积分第一中值定理进行计算.

进一步有

下面，固定A，由g(x)在[0,A]上连续可知，存在正数M，使得当x∈[0,A]时，|g(x)|≤M，从而|g(x)-c|≤M+|c|. 因此，

注 对例5和例6，在证明积分极限为0时，可以将区间分成两段：一段上函数有界，可将区间长度取为任意小，然后固定分点；另一段区间长度有限，函数一致趋于零，从而两段上的积分都任意小，结合数列极限的定义即可得到结论.

4 结语

本文总结的积分极限的几种常用计算方法，期望能够为相关课程的教学提供参考. 面对复杂的积分极限问题，只有通过不断思索、不断尝试，注重科学思维方法的训练，才能培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感，逐步提高学生面对困难的想象力和创造力，以及分析问题、解决问题的能力.