等截面摩擦管流输运自由流阻力颗粒计算模型
2022-05-19孙科薛文鹏郭佳男王欢
孙科, 薛文鹏, 郭佳男, 王欢
(中国飞行试验研究院发动机所, 西安 710089)
为探明航空发动机在吸入冰雹等恶劣条件下的适应性,通常需要进行试验,充分验证发动机在极端环境下的工作稳定性,以保证实际飞行过程中的安全可靠。中外航空机构均制定了相应的适航条款,如美国航空局制定的FAR 33部[1]中第33.78条即规定发动机需在工作包线范围内,遭遇任意30 s的连续冰雹时,具有可接受的工作能力,欧洲航空安全局(EASA)也制定了相应的适航条款[2]。中国民航局于2002年制定了对应的适航条款[3]。有学者进行了吸雹适航条款研究[4],考核发动机在吸雹时的工作稳定性,需向发动机进口抛射一定流量的冰雹。根据国外发动机试验经验,一般需在数秒内向发动机入口持续抛射数以万计的小冰雹。通常采用压缩气体气力输运冰雹,在抛射管中气体膨胀加速,高速气流输运冰雹,使其向前加速运动,以较高的速度离开抛射管,并继续运动至发动机入口。气力输运原理常用于油井生产[5]、煤粉运输[6]等。压缩空气在抛射管内的流动过程直接影响冰雹运动过程,前人针对管内流动做了大量研究。刘自龙等[7]针对水平管内油气两相流进行了压降模型研究;杨矞琦等[8]针对垂直管内的稠油-水两相高温高压流动进行了压降规律研究;叶爽等[9]通过实验及计算研究了综合管廊热力管道的最佳通风区;廖柯熹等[10]总结了天然气管网系统性能计算研究方法进展。
针对压缩气体气力输运抛射管中连续冰雹的问题,建立基于等截面摩擦管流和颗粒自由流阻力的颗粒输运计算方法。将压缩气体流动系统简化为流体网络模型,其中各元件均有相应的工程计算方法。使用自由流阻力模型进行颗粒运动过程及运动速度的计算。
1 冰雹抛射运动过程
在抛射管入口处连续投放冰雹,并且向抛射管入口通入高压空气。由于冰雹与气流间的速度差,两者之间产生动量交换,在压缩空气拖曳力的作用下,颗粒产生加速,直至离开抛射管。为求解冰雹运动过程,首先需求解冰雹在抛射管中的受力情况,因此需求解在抛射管内部气流的流动情况,速度分布及压缩气体流量。
流体网络法将流动系统简化为由典型元件组成的工程计算模型,元件特性通过理论或实验方法获取,具有快速实用性,因此是一种应用广泛的工程计算方法,普遍应用于航空发动机空气系统计算[11-15]及管路系统[16]等相关领域。应用流体网络法,将压缩气体流动过程简化为典型的流体网络模型,如图1所示。其由管元件、突扩元件及入口节点、出口节点等组成。计算中给定抛射气源压力、抛射气源温度及出口压力,即可计算得到压缩气体流量及各元件入口及出口的压力、速度分布。

图1 流体网络模型Fig.1 Fluid network model
2 气力输运计算方法
2.1 等截面摩擦管流
为分析冰雹在抛射管内部的运动过程,需对气流在抛射管内的运动过程进行计算。一维等截面摩擦管流在气流膨胀、壁面摩阻及边界层充分发展的作用下,气流加速运动。图2为等截面摩擦管路的微元段。对于微元段dx而言,其受到上游气流的压力为p,受到下游气流压力为dp。
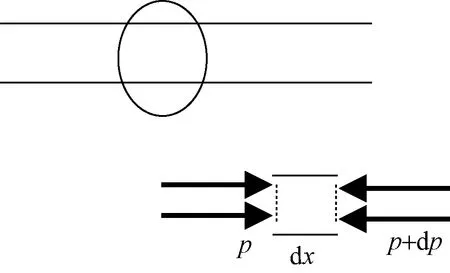
dx为微元段长度图2 等截面管微元段Fig.2 Infinitesimal section of constant cross section tube
抛射管为等截面,由于气流速度较快,假设气体与外界没有机械功和热量的交换。式(1)为等截面摩擦管流在微元段上的总压差方程式[17],其与气流马赫数及壁面摩阻、管道直径有关。

(1)
式(1)中:p*为气流总压,Pa;dp*为在微元段上的总压差,Pa;k为绝热指数,空气取1.4;Ma为气流马赫数;Cf为壁面摩阻;dx为微元段长度,m;d为等截面摩擦管的管径,m。
将式(1)进行转化即可得到总压随管长度方向的变化关系,可归结为关于管长坐标值x与p*的函数关系f(x,p*),可表示为
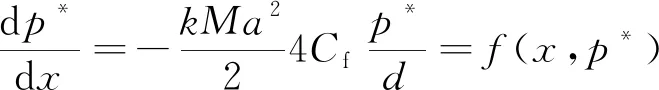
(2)
使用Runge Kutta法[18]求解式(2)的常微分方程,求解方法为

(3)
由于等截面摩擦管流与外界无机械功或热的交换,在给定的边界条件下,即给定入口总压、入口总温、流量,便可得到等截面摩擦管流沿程的总压分布。根据流量函数方程式[式(4)],通过总压、流量、总温,便可得到气流马赫数,及气流速度、气流静温、气流静压等参数。

(4)
管路壁面摩阻计算公式为

(5)
式(5)中:Re为雷诺数。
2.2 自由流颗粒计算方法
使用自由流阻力模型对颗粒的受力情况进行分析,受力和颗粒与流体间速度差、流体密度及阻力系数等有关。
颗粒受力FR的计算公式为[19]
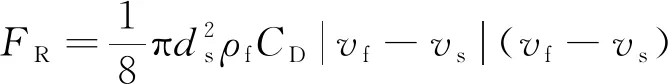
(6)
式(6)中:下标s为固体颗粒;下标f为流体;ds为冰雹颗粒直径,m;ρf为流体密度,kg/m3;vf为流体速度,m/s;vs为冰雹颗粒速度,m/s;CD为阻力系数。
阻力系数取决于颗粒流动雷诺数Res,其表达式为
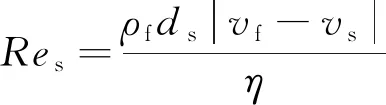
(7)
式(7)中:η为流体动力黏度。
阻力系数计算公式为

(8)
3 计算结果分析
3.1 等截面摩擦管流分析
在基本工况条件下,对压缩气体在管路中的流动进行分析,图3为流体计算区域。基本工况对应的等截面管道管径为45 mm,管长为5 m。计算过程中,流体介质根据实际情况设定为可压缩空气,介质密度采用理想气体状态方程进行计算。基本算例中,设置抛射气源压力为220 kPa,抛射气源温度为300 K,出口压力设置为97 kPa。
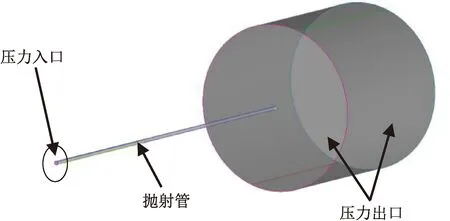
图3 流体计算域Fig.3 Fluid computing domain
图4为等摩擦管流沿程总压计算结果,在管长增大方向,由于壁面摩阻作用,总压不断降低。图5为沿程速度计算结果,由于气流膨胀,造成压力降低且密度减小,随着边界层充分发展,沿程速度逐渐增大。

图4 沿程总压计算结果Fig.4 Results of total pressure along the way
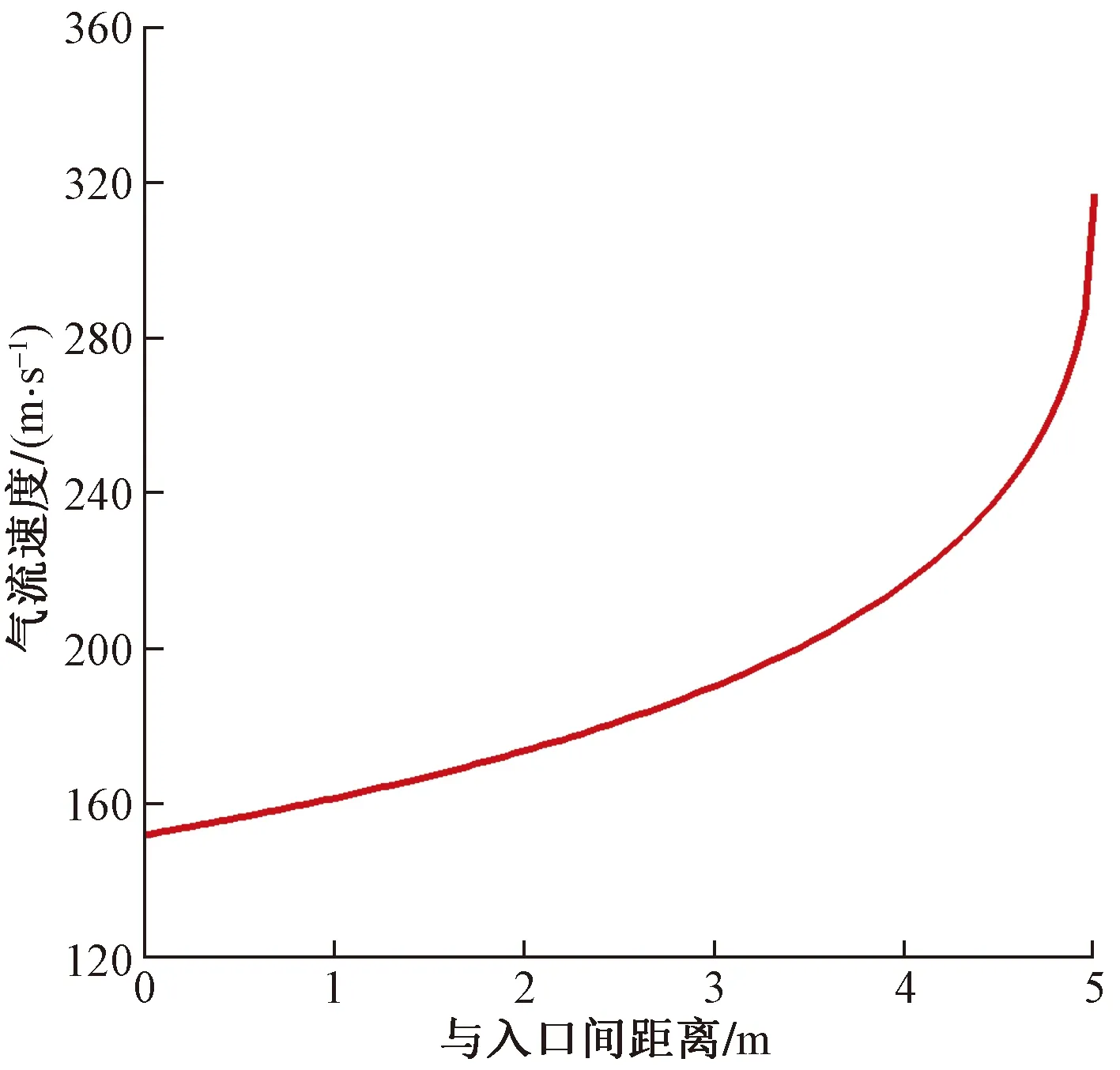
图5 沿程速度计算结果Fig.5 Results of velocity along the way
3.2 颗粒运动过程分析
应用等截面摩擦管流计算结果,对冰雹颗粒在抛射管内的运动及受力情况进行分析计算。在颗粒投放至抛射管的起始时刻,其处于抛射管入口处,以冰雹抛射管入口处为零点,以气流流动方向为正方向,即抛舍管入口处x=0;由于颗粒从管外沿径向投放至抛射管内,因此起始时刻在x方向上的速度vx为0,即vx=0。根据抛射管内部沿程气流速度、压力等参数分布情况,对冰雹加速过程进行计算。基本算例中,冰雹颗粒密度设置为861 kg/m3,冰雹直径设置为13 mm。
图6为冰雹颗粒加速度随时间的变化情况,由于在初始时冰雹速度较小,与空气间的速度差较大,因此冰雹所受的输运力较大,从而在初始时刻冰雹的加速度较大,随着冰雹的速度增大,其与空气的速度差逐渐减小,动量交换程度逐渐减弱,因此加速度逐渐减小。

图6 加速度随时间变化情况Fig.6 Acceleration versus time
图7为冰雹速度随时间的变化规律,由于在初始时刻,冰雹运动加速度较大,因此在x=0位置处,曲线斜率较大,随着加速度逐渐减小,冰雹速度增长趋势逐渐缓慢。
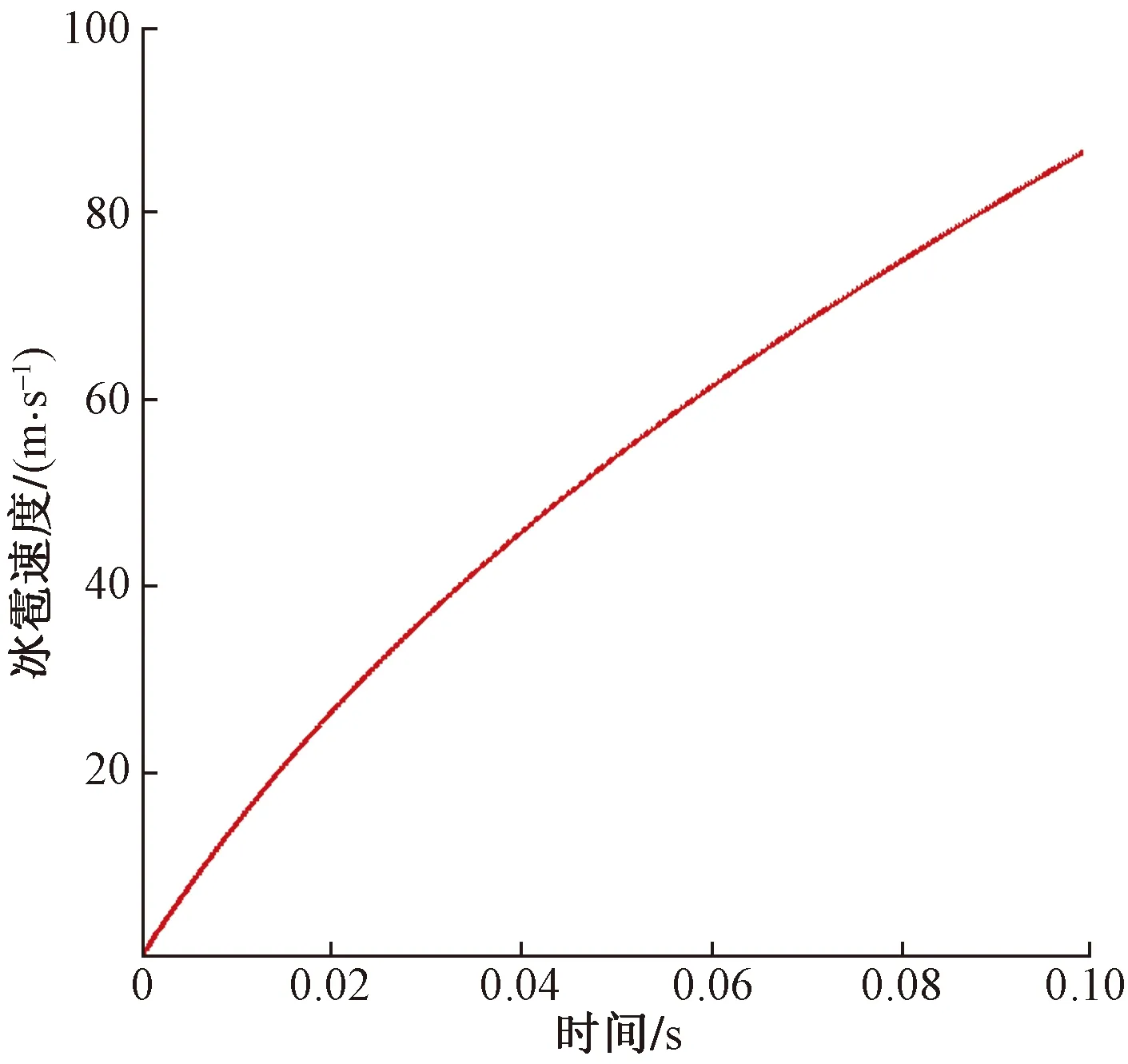
图7 速度随时间变化情况Fig.7 Speed versus time
图8为冰雹位置随时间的变化情况,随着时间推移,冰雹速度逐渐增大,曲线斜率逐渐增大。直至时刻t=0.991 s,冰雹离开抛射管。此时速度为86.43 m/s。

图8 位置随时间变化情况Fig.8 Position change over time
3.3 气力输运影响因素分析
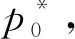
首先对抛射气源压力不同情况下的冰雹抛射速度进行分析,计算抛射气源压力分别为150、180、220、260、300 kPa时对应的空气流量及冰雹抛射速度。如图9所示,随着气源压力增大,空气流量直线式增大。如图10所示,冰雹抛射速度随着气源压力增大也在增大,但增长趋势逐渐放缓。由于当气源压力增大到一定程度时,抛射管出口处气流速度达到当地声速,但由于入口总压的增大,出口处的气流密度增大,因此冰雹出口速度依然增大。由于冰雹速度的增大,气流与冰雹间速度差的减小,抛射气源压力增大对抛射速度的增大效果逐渐减小。

图9 空气流量随抛射压力变化情况Fig.9 Variation of air flow with ejection pressure

图10 出口速度随抛射压力变化情况Fig.10 Change of outlet velocity with ejection pressure
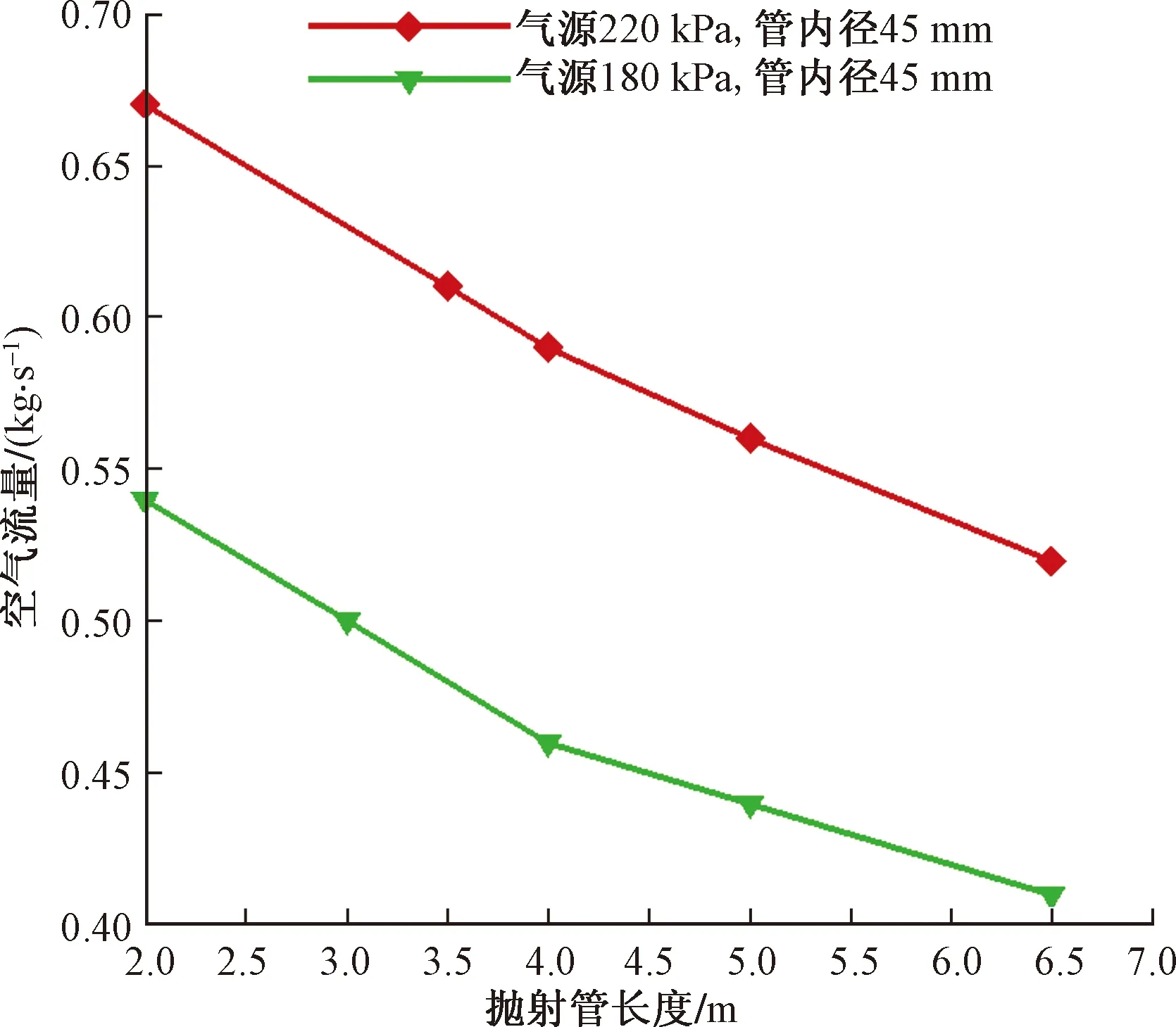
图11 空气流量随管长变化情况Fig.11 variation of air flow with pipe length
其次,对抛射管长度造成空气流量及冰雹抛射速度的变化进行分析计算。图11为气源压力分别为220、180 kPa,抛射管内径45 mm时,不同抛射管长度下的空气流量计算结果。图12为冰雹抛射速度计算结果。随着抛射管长度的增大,沿程损失增大,空气流量逐渐减小;冰雹抛射速度先增大,后基本保持不变,这是由于管长较长会造成空气流量降低,从而输运冰雹颗粒的驱动作用削弱,另外由于冰雹速度的增大,其与气流间速度差减小,自由流阻力逐渐减小。因此,管长一般小于5 m即可。
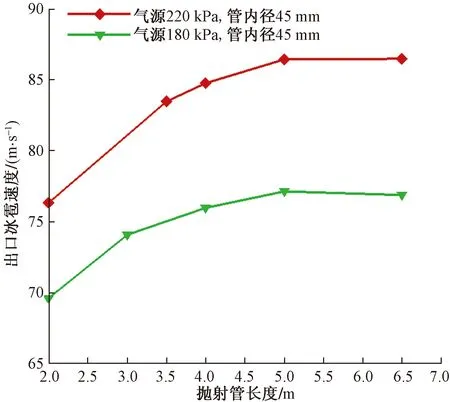
图12 出口速度随管长变化情况Fig.12 Variation of outlet velocity with pipe length
图13、图14为抛射管内径不同对空气流量及冰雹抛射速度的影响计算结果。随着抛射管内径的增大,空气流量指数级增长,冰雹抛射速度也在不断增大,这是由于空气流量增大,即驱动冰雹颗粒运动的驱动力增大。但由于冰雹速度增大,与气流间速度差减小,自由阻力逐渐减小。在进行抛射管设计时,其内径不应过大,避免造成压缩空气消耗量过大。

图13 空气流量随管径变化情况Fig.13 Variation of air flow with pipe diameter
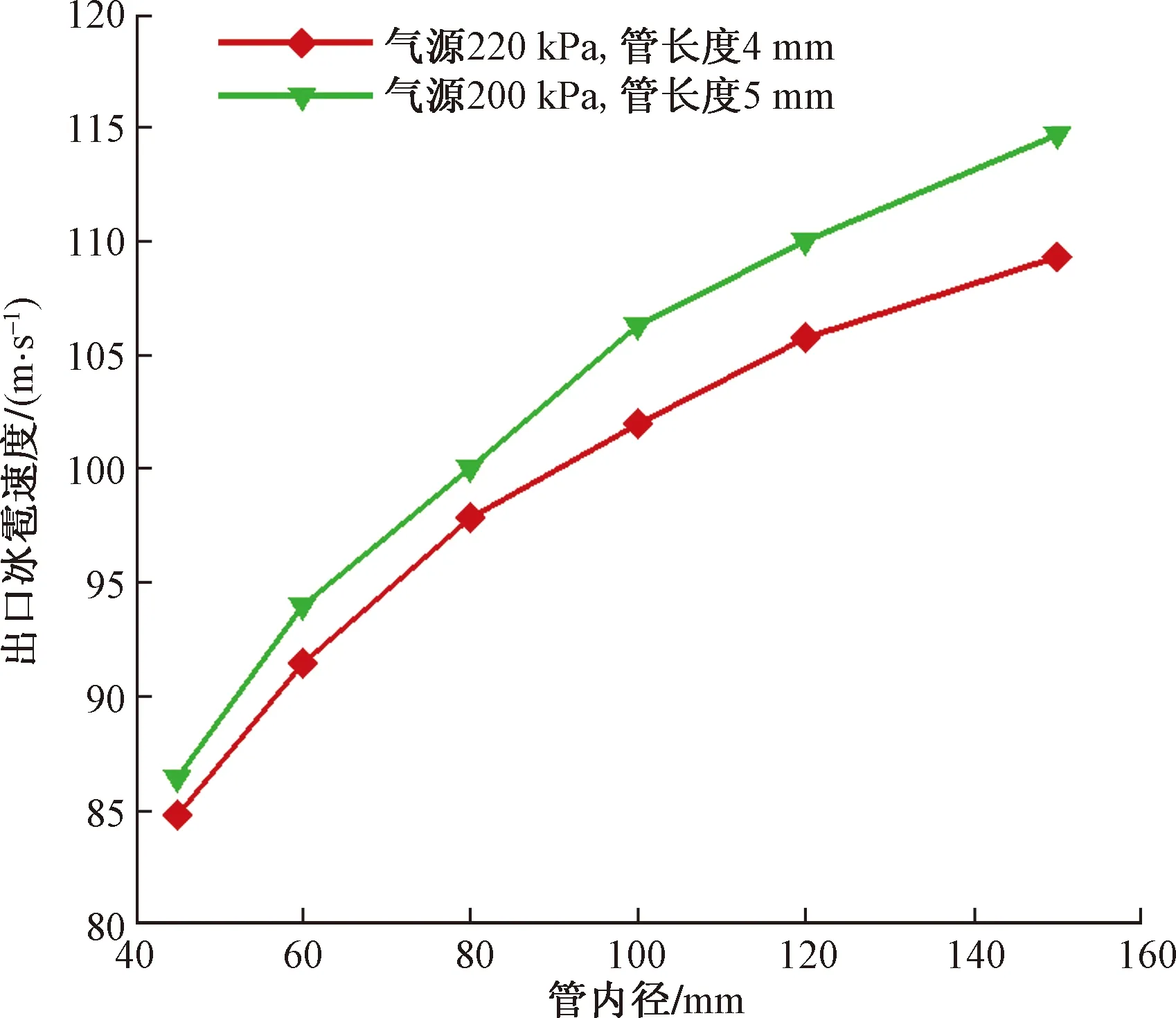
图14 出口速度随管径变化情况Fig.14 Variation of outlet velocity with pipe diameter
4 结论
针对压缩气体气力输运冰雹颗粒的问题,主要研究在抛射管内部压缩空气参数变化规律及冰雹颗粒运动情况。得到以下主要结论。
(1)建立了基于流体网络法的工程计算模型,由管元件及突扩元件等组成,给定入口节点总压、总温及出口节点压力,即可计算得到系统中各关键节点压力、温度分布及系统空气流量。
(2)使用等截面摩擦管流常微分方程描述抛射管内部总压的变化规律,在入口压力及流量已知的情况下,组成常微分方程的初值问题,应用Runge-Kutta法求解该问题,即可得到各关键参数的沿程变化情况。
(3)使用自由流阻力模型对颗粒的受力进行计算,从而获取颗粒的运动情况;对影响冰雹抛射速度的关键因素进行了分析计算。随着抛射气源压力的增大,空气流量逐渐增大,冰雹抛射速度逐渐增大,但增长趋势逐渐缓慢;随着抛射管长度的增大,空气流量逐渐减小,冰雹抛射速度先增大后基本不变;随着抛射管直径的增大,空气流量指数型增长,冰雹抛射速度逐渐增大,但增长趋势逐渐缓慢。分析计算结果,提出冰雹抛射管的关键尺寸设计要求,抛射管内径45 mm,抛射管长5 m。对于这种设计结构,在抛射管入口压力为220 kPa时,消耗空气流量较小,为0.56 kg/s;冰雹抛射速度较大,可达86 m/s。
