基于刚度协调的路桥过渡段路面疲劳寿命预估

栾利强， 文双寿， 张婧怡， 肖桂元， 赵瑞宇

(广西岩土力学与工程重点实验室， 桂林 541004； 2.桂林理工大学土木与建筑工程学院， 桂林 541004)

沥青路面疲劳破坏是中国路面破坏主要形式[1]，近年来伴随交通量的日益增长和荷载等级的不断提高，桥头搭板处沥青路面铺装层的疲劳破坏情况越来越严重[2]，维修周期也越来越短，花费了大量的财力与物力，严重影响了行车舒适性和安全性。学者们针对桥头跳车开展了大量研究。邓露等[3]以局部冲击作为桥梁安全指标，提出了基于行车安全性和舒适性的允许台阶高度确定方法以及更高的控制指标；郑少年等[4]建立动态三维模型，并自编子程序，分析了车速、材料阻尼比等因素对路面响应的影响；姚辉等[5]建立了四轮双轮载重车辆动力运动模型，得到公路桥头跳车的车辆动力运动方程，并计算得到搭板处存在应力集中现象，需要进行补强设计。这些成果都推动中国治理桥头跳车研究进程，为工程治理提供了理论依据，但未能从本质上解决跳车问题，只是在一定程度上减缓了其破坏的进程。

桥头跳车本质上是由于路桥刚度差异过大产生不均匀沉降，进而结构发生开裂断裂的现象[6]，协调结构刚度，提高疲劳寿命是从本质上解决桥头跳车方法之一，现有的疲劳寿命模型未考虑结构刚度(即材料模量和厚度)以及车速、轴载等多因素的综合影响[7-8]，特别是在路桥过渡段有大刚度桥头搭板的情况下，结构层间刚度差异过大，沥青混凝土面层层底处于受压状态[9]，通过传统的疲劳模型进行路桥过渡段结构层设计与预估不再适合。基于此，考虑了结构刚度与车速、轴载等多因素综合作用，分析路桥过渡段路面应力强度因子、疲劳寿命在不同结构层刚度差下变化发展规律，建立了结构组合以及力学指标多因素桥头搭板处沥青面层疲劳寿命预估模型，为中国从本质上治理桥头跳车提供一种新方法。

1 数值模型的建立

1.1 基本假设

①假设路桥过渡段路面结构层之间均处于完全连续、各向同性、匀质的线弹性材料，满足胡克定律；②只考虑行车荷载作用，不考虑温度荷载对裂缝影响；③不考虑搭板和地基之间的摩擦力，不计桥台与结构层的摩阻力，路表绝对水平，不考虑路表面与轮压的水平作用力；④假设路面结构都存在初始裂缝，初始裂缝深度对路面疲劳寿命影响较大，参考文献[10]将沥青路面的初始裂缝定义为7.5 mm，根据Li[11]根据材料测得初始裂缝深度为6.9 mm研究结论，取初始裂缝长为7.0 mm。

1.2 行车荷载及作用形式

艾长发等[12]、栾利强[13]、赵之仲等[14]、葛辉等[15]研究表明，对称荷载作用下，张开型应力强度因子KⅠ为负值，裂缝处于闭合状态，路面疲劳破坏主要是由偏荷载作用引起的，因此只考虑偏荷载作用下的应力强度因子KⅡ随不同刚度结构的变化规律以及偏荷载作用下的疲劳寿命分析。车辆荷载根据《公路沥青路面设计规范》(JTG D50—2017)[16]采用轴重为100 kN的单轴-双轮组轴载加载，轮压p=0.7 MPa，轮载P=25 kN，轮胎与路面接触面积可简化为两个半圆和一个矩形，为了方便加载计算，根据静力等效进一步简化为一个213 mm(长)×167 mm(宽)矩形如图1所示。

图1 荷载布置及车轮简化示意图Fig.1 Schematic diagram of load arrangement and wheel simplification

车辆荷载在路桥过渡段作用时间短，且路面多为不平整，车轮与路面接触作用复杂，为了更好地表征车辆荷载在有限元的实现，把车辆荷载简化为重复循环半正弦波荷载。路面材料具有一定的弹塑性，在车辆荷载作用过后有一定的自恢复时间，半正弦荷载可以很好地体现沥青路面在车辆荷载作用下瞬时性和冲击性。车辆荷载简化后的半正弦荷载表达式为[17]

(1)

式(1)中：P(t)为随时间t变化的动态荷载；Pmax为0.7 MPa；ω为角频率，T为荷载的作用周期，T=12l/v,其中，l为轮胎接地面积，常规车辆一般取15 cm，v为汽车行驶速度，汽车速度以65 km/h为例，计算得到荷载作用周期T=0.1 s。

1.3 路面结构及材料参数

在快速移动的汽车荷载作用下，面层动态回弹模量能更加准确的反映汽车在路面上的真实动态响应。基层、底基层和土基埋深比较大，受汽车移动荷载影响较小，故采用静态模量，根据中国半刚性基层沥青路面的在路桥过渡段的典型路面结构，采用深埋式混凝土搭板5层体系结构，路面结构层厚度及材料动态参数[18-19]如表1所示。

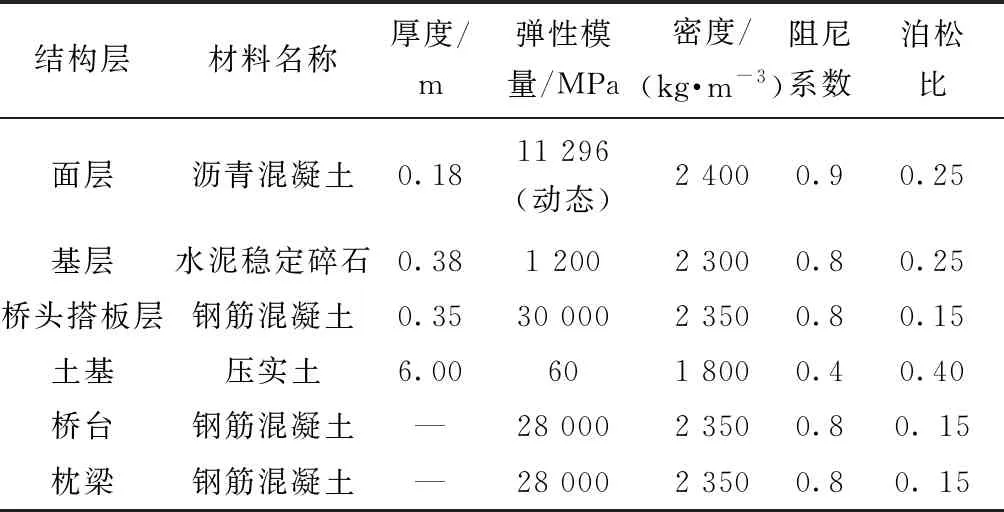
表1 模型动态分析材料参数

1.4 ABAQUS有限元模型的建立

根据路桥过渡段受力特点，建立图2所示的路桥过渡段路面疲劳裂缝有限元模型，模型的长为8.5 m、宽6 m、高7 m，桥头搭板长为8 m、宽6 m、厚0.35 m[20]，其余结构层主要参数如表1所示，结构单元采用C3D8R单元，共57 600个。土基为半无限体空间，模型底面完全约束，顶面加载不做约束，前、后、左、右面约束法线方向及转动。裂缝网格加密划分，如图3所示。

图2 路桥过渡段路面疲劳裂缝有限元模型Fig.2 Three-dimensional finite element model of road surface structure in transition section of road and bridge

图3 裂缝处网格划分Fig.3 Mesh division at the crack

2 裂缝应力强度因子分析

桥头搭板刚度过大，而沥青混凝土面层一般为柔性材料，此处路面结构层间极不协调，为探究路面在不同结构刚度差下的断裂性能，以表1数据为基础，对不同结构层间刚度差下应力强度因子KⅡ进行研究，结果如图4所示。

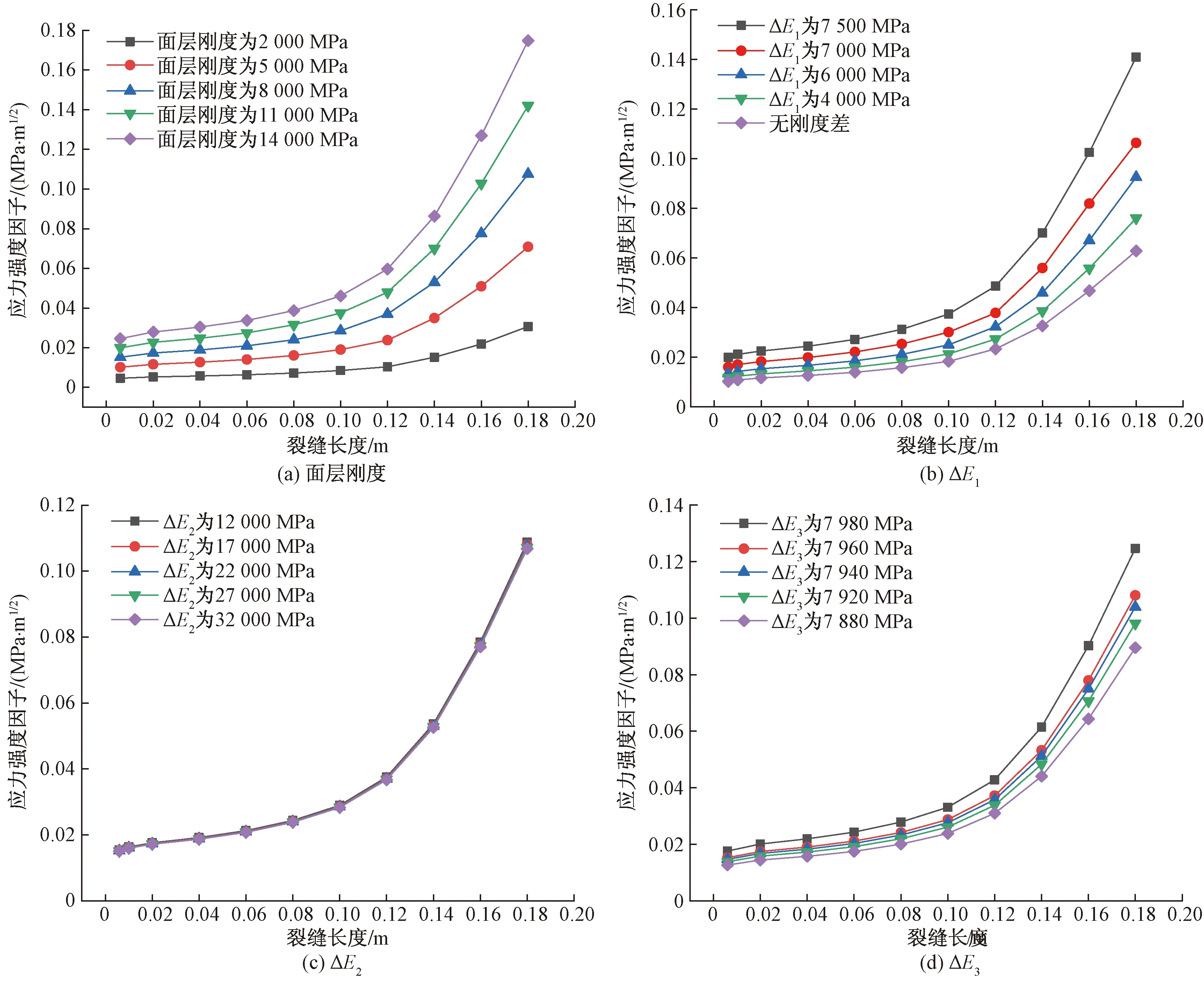
ΔE1为面层与基层刚度差；ΔE2为面层与桥头搭板层刚度差；ΔE3面层与土基刚度差图4 KⅡ 随面层刚度、ΔE1、ΔE2、ΔE3变化规律Fig.4 KⅡ changes with the stiffness of the surface layer, ΔE1，ΔE2，ΔE3

由图4可知：在偏荷载作用下，应力强度因子KⅡ随着面层刚度的增长而递增；随着面层与基层刚度差、面层与桥头搭板层刚度差、面层与土基刚度差的减小而减小。当面层模量过大时，路面结构整体刚度变大，应力更加集中，加速了裂缝扩展断裂，

当面层与基层刚度差、面层与土基刚度差减小时，刚度突变得以缓解，应力集中现象减弱，裂缝扩展速度变慢；随着裂缝长度的增加呈递增比例增加。裂缝长度在8 cm之前，应力强度因子值趋于平稳，裂缝扩展速度缓慢，当裂缝长度在大于8 cm时，应力强度因子急剧增大，裂缝尖端应力集中越明显，加快了裂缝扩展速度。面层与桥头搭板层刚度差对裂缝扩展基本没有影响，通过增大桥头搭板层刚度来减缓面层疲劳裂缝扩展速度是不可取的。

3 桥头搭板处沥青面层疲劳寿命分析

3.1 单因素作用下沥青混凝土面层疲劳寿命变化规律分析

根据广义Paris预估模型计算疲劳寿命，其计算公式为

(2)

式(2)中：N为沥青混凝土面层疲劳寿命；a0为裂缝初始长度，取7.0 mm；a为临界裂缝长度，即整个面层厚度；C和n为材料参数；ΔK为应力强度因子幅值(交变应力最大值与最小值对应的应力强度因子之差)。

材料参数C和n通过室内小梁剪切疲劳试验得到面层裂缝扩展速率曲线，建立小梁疲劳有限元模型对裂缝扩展速率与应力强度因子取双对数进行线性回归得到Paris参数[13]，如表2所示。

表2 沥青混凝土Paris模型计算参数

将上、中、下面层三层沥青混凝土看作一层，即把面层各结构层间的材料看成同一种材料，根据沥青层的厚度对沥青层赋予权重，简化得到沥青混凝土一层沥青混合料的Paris模型计算参数如表3所示。

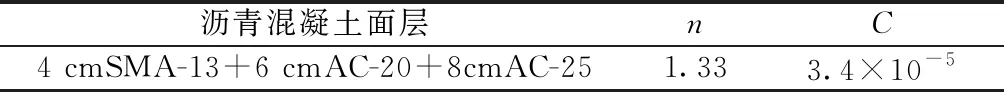
表3 面层简化后Paris模型计算参数

根据简化后沥青面层Parise模型计算参数(表3)对不同结构刚度下疲劳寿命单因素进行分析，结果如图5所示。可以看出：沥青混凝土面层疲劳寿命随着面层模量、轴载增长而减小，随着面层厚度、基层模量、基层厚度、搭板层模量、搭板层厚度、土基模量、车速增长而增大。

面层厚度对自身疲劳寿命的影响非常显著，面层厚度由12 cm上升至36 cm，疲劳寿命提高了约3.5倍，面层厚度的增大，不仅增大了扩展路径距离，同时也提高了路面结构层整体刚度。詹苏涛[21]研究表明，桥台与路堤刚度越协调，汽车经过时轮压接地放大倍数越小，较未协调刚度之前轮压减小，不均匀沉降也减小；在双重效果作用下，沥青面层疲劳寿命得以显著提高。面层模量增大，面层整体刚度也会增大，剪应力增大，裂缝更易于扩展，与面层厚度不同的是，面层厚度增长间接增加刚度，且裂纹扩展路径距离对疲劳寿命的影响远大于模量的影响。基层模量和桥头搭板层模量对面层疲劳寿命影响甚微，基本可忽略不计。

面层疲劳寿命随着土基模量增长呈线性增大，土基模量从20 MPa提高至120 MPa，面层疲劳寿命提高约2.8倍，土基固结与流水侵蚀容易使搭板与土基脱空，整个路面结构承受较大的弯矩和挠曲变形，增大土基模量，路面结构层整体刚度将提高，减小了路堤与桥台、路面与土基的刚度差，提高了面层疲劳寿命，因此路桥过渡段应着重处理土基刚度，避免刚度差过大引起应力集中，进而产生裂缝甚至发生结构物断裂破坏。

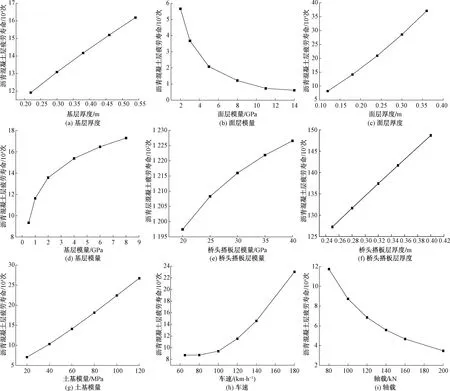
图5 不同结构刚度下疲劳寿命的变化Fig.5 Variation of fatigue life under different structural stiffness

桥头搭板层厚度由25～40 cm，面层疲劳寿命提高16.9%，提高效果一般，增大桥头搭板厚度和模量，桥头搭板自身刚度会变大，对于混凝土材料，其抗拉强度非常低，一旦刚度过大，变形能力减弱，极易开裂，桥头搭板自身疲劳寿命会急剧减小，在处理搭板时，应综合考虑其抗裂性能，不能一味地追求其刚度，适当降低搭板刚度有利于整体结构的疲劳寿命，在工程上应提高其配筋率以保证有足够的抗拉抗裂能力。

车速由65～180 km/h,疲劳寿命提高了1.6倍，车辆荷载与路面作用时间及路面结构变形具有瞬时性，提高车速，瞬时性越显著，路面产生变形很小或无变形，沥青路面疲劳寿命明显提高；当然这只是针对路表绝对平整，未考虑水平摩擦力和路面不平整的汽车冲击力，车速越大，水平摩擦力和冲击力越大，理想状态下车速愈快愈好，但实际情况会有偏差；轴载由80～200 kN,面层疲劳寿命降低了70.4%，在长期超载作用下面层疲劳寿命显著降低。

3.2 疲劳寿命单因素敏感性分析

为了研究在单因素作用下对疲劳寿命的影响显著性，采用敏感性系数进行分析，计算公式为

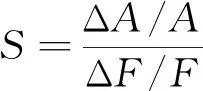
(3)

式(3)中：S为敏感度系数；A为初始疲劳寿命；ΔA为影响因素发生ΔF变化时疲劳寿命变化值，ΔA/A为单因素作用下疲劳寿命变化率；F为影响因素初始值；ΔF为影响因素的变化值，ΔF/F为不确定的单因素变化率，其计算结果如表4所示。

表4 敏感度系数

各因素对沥青混凝土面层疲劳寿命影响显著性为：面层厚度>车速>土基模量>轴载>搭板层厚度>基层厚度>面层模量>基层模量>搭板层模量。

4 路桥过渡段路面疲劳预估模型

4.1 动态响应分析

根据《公路沥青路面设计规范》(JTG D50—2017)[16]设计指标，现对路桥过渡段沥青混合料层层底拉应变基层层底拉应力、基层顶面竖向压应力等力学指标进行疲劳寿命非线性回归分析，以初始裂缝7.0 mm为例，其散点图及拟合回归曲线如图6所示。根据图6回归得到曲线方程如表5所示。

根据表5对比分析可知：沥青层底拉应变对沥青混凝土路面进行疲劳寿命回归效果最好，因此采用沥青层低拉应力作为力学指标进行多因素回归。

图6 沥青混合料层力学指标与疲劳寿命散点图及回归曲线Fig.6 Scatter diagram and regression of curve of mechanical index and fatigue life of mixture layer

表5 各控制指标下散点图拟合回归曲线方程

4.2 多因素作用下的疲劳预估方程

由单因素敏感性分析结果，不考虑面层模量、基层模量、桥头搭板层模量对路桥过渡段沥青混凝土层疲劳寿命的影响，保留面层厚度、基层厚度、桥头搭板层厚度、土基模量、车速和轴载。以中国沥青混合料层疲劳开裂公式及国外疲劳预估模型为参照文献[22]，同时考虑结构组合和力学控制指标，在保证各因素正确的意义上，初步建立桥头搭板处面层疲劳寿命预估模型为

(4)

式(4)中：Nf为沥青混凝土面层疲劳寿命；H1为面层厚度；H2为基层厚度；H3为桥头搭板层厚度；Es为土基模量；v为车速；load为轴载；εa为沥青混合料层底拉应；a、b、c、d、e、f、g为参数。

采用5水平6因素，即L25(56)试验进行多因素作用下疲劳寿命计算与非线性拟合回归分析如表6、表7所示。

根据正交分析计算结果，采用自定义方程Levenberg-Marquardt迭代算法，进行非线性拟合回归得到桥头搭板处沥青混凝土面层疲劳寿命预估模型为

R2=0.912

(5)

表6 正交分析因素水平

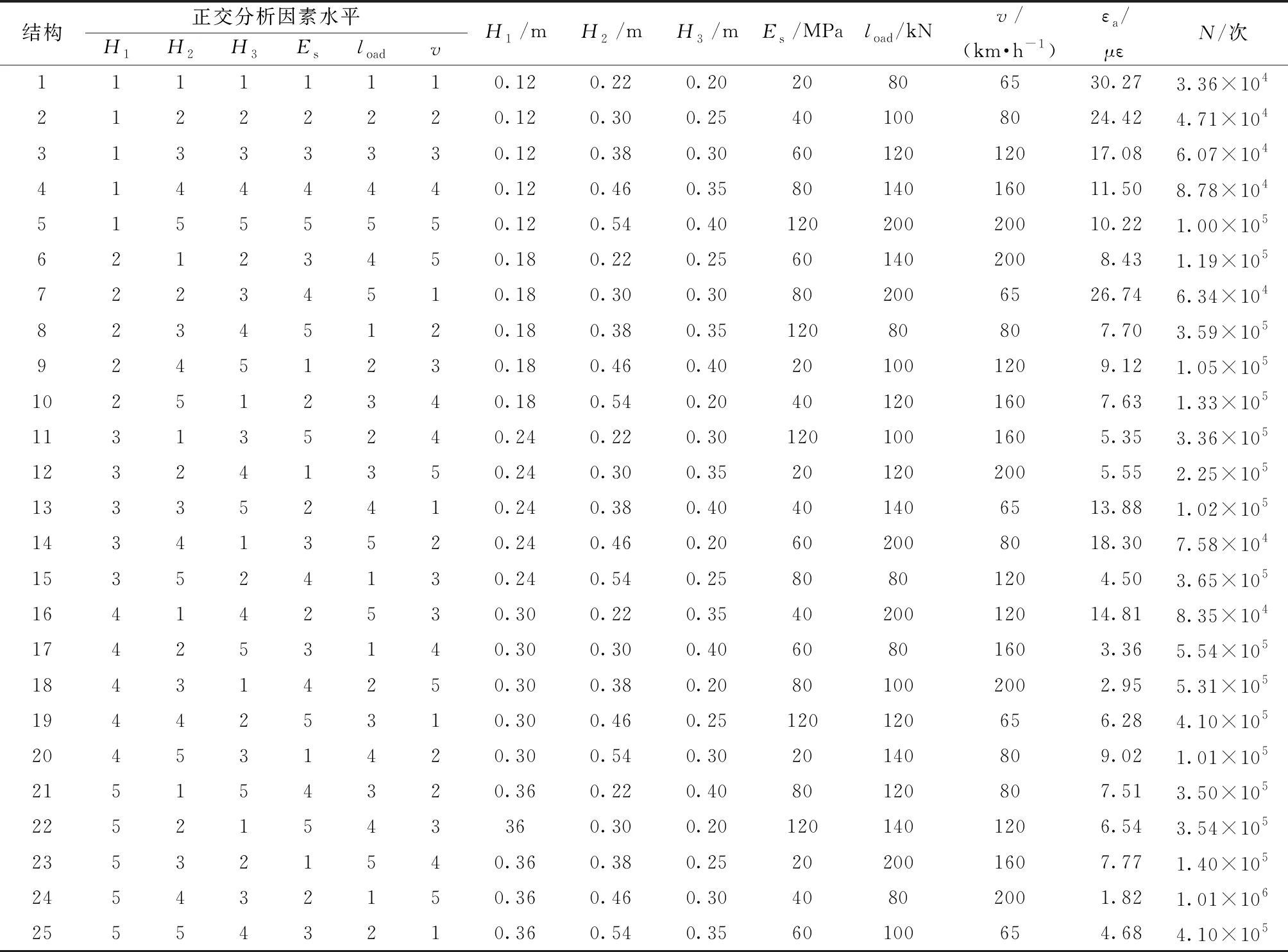
表7 L25(56)试验

通过式(5)可以看出，该模型相关性系数R2=0.912，具有较高的非线性拟合规律，该模型可以根据层间厚度，模量等多因素预估沥青面层疲劳寿命，协调刚度进行最佳费用与最大寿命协调设计，同时可为超、重载、低速特别是有大刚度桥头搭板等特殊路面结构和特殊路况地区合理设计提供理论参考。

5 结论

通过路桥过渡段受力特点，建立ABAQUS三维有限元分析模型，通过断裂力学分析了偏荷载作用下不同结构层刚度差下应力强度因子变化规律，对沥青混凝土面层疲劳寿命的单因素与多因素的一系列分析，得到以下结论。

(1)应力强度因子KⅡ随着面层模量的增长而增大，随着面层与基层刚度差、面层与桥头搭板层刚度差、面层与土基刚度差的减小而减小；刚度协调(刚度差减小)之后能有效降低疲劳裂缝的扩展速度，增大疲劳寿命，裂缝越长应力强度因子越大，加速了疲劳扩展断裂进程。

(2)面层疲劳寿命随着面层模量、轴载增长而减小，随着面层厚度、基层模量、基层厚度、搭板层模量、搭板层厚度、土基模量、车速增长而增大，通过敏感性分析得到各影响因素对面层疲劳寿命显著性为：面层厚度>车速>土基模量>轴载>搭板层厚度>基层厚度>面层模量>基层模量>搭板模量。

(3)面层厚度对自身疲劳寿命的影响非常显著，面层厚度由12 cm增大至36 cm，疲劳寿命提高了约3.5倍，面层疲劳寿命随着土基模量增长呈线性增大，土基模量从20 MPa提高至120 MPa，面层疲劳寿命提高约2.8倍，在处理桥头搭板处沥青路面时应着重加强对土基的处理，避免土基过大的固结沉降造成应力集，进而结构物开裂等破坏降低疲劳寿命。

(4)桥头搭板层厚度由25～40 cm，面层疲劳寿命提高16.9%，提高效果一般，通过增大桥头搭板层厚度来提高面层疲劳寿命是不可取的。车速由65～180 km/h,疲劳寿命提高了1.6倍，车速越快接触模量越大，形变越小；轴载由80～200 kN，面层疲劳寿命降低了70.4%，在长期超载作用下面层疲劳寿命显著降低。

(5)通过荷载响应、正交分析计算与非线性拟合回归分析，建立了在力学控制和结构组合综合作用下路桥过渡段处沥青混凝土面层疲劳寿命预估模型，对从根本上解决桥头跳车及提高路面耐久性有重要意义，为中国在超、重载、低速特别是有大刚度桥头搭板等特殊路面结构和特殊路况地区合理设计提供理论参考。