基于离散型二项式系数组合模型的黄土湿陷性评估

任文博， 刘云龙*， 李佳佳， 李硕磊, 李文庆

(1.郑州大学土木工程学院， 郑州 450001； 2.中国建筑第七工程局有限公司， 郑州 450004)

黄土是一种在干旱和半干旱环境中形成的特殊沉积物，在中国分布广泛,约为6.3×105km2，其中60%为湿陷性黄土[1-2]。湿陷性黄土一般天然含水量较低且结构松散拥有大孔隙，当土体处于低含水量状态下强度高压缩性低。然而一旦受到雨水的渗入，土体结构被破坏，强度降低，压缩性提高，在土体自重或上覆荷载作用下，土体被压缩，产生湿陷变形[3]。由于以上特性，湿陷性黄土地区的建筑在受到生活用水，管道泄漏和降雨等状况时极易出现地基沉降，结构开裂和建筑物倾斜等工程问题[4]，因此对黄土湿陷性进行评估至关重要。

黄土的湿陷现象是一个多因素耦合作用的物理化学过程。目前中外解释黄土湿陷的假说众多，如可溶性盐假说、毛细血管假说、欠压密假说和微结构不平衡吸力假说等，但均不能很好的解释黄土的湿陷性，因此一般采用试验的方法对黄土湿陷性进行评估[5-6]。黄土的湿陷性一般用湿陷性系数δs来评估，湿陷性系数为在规定压力下浸水黄土单位厚度土层的湿陷量，当δs≥0.015时为湿陷性黄土。此外，根据湿陷性系数的大小可将湿陷性黄土分为轻微湿陷性黄土(0.015<δs≤0.030)、中等湿陷性黄土(0.030<δs≤0.070)和强烈湿陷性黄土(δs>0.070)[7]。目前，黄土湿陷性系数的测定方法分为两种，一种为现场试验，另一种为室内试验。现场试验结果较准确，但周期长投资大，故一般采用室内试验进行湿陷性系数测定。室内试验方法又分为双线法和单线法，虽室内试验相对于现场试验较易实现，但由于测定工作量庞大，步骤烦琐，仍需投入大量的人力、物力和时间且测量精度有限[3]。相对于湿陷性系数，土体的常规物性指标，如孔隙比、干密度、含水量、塑限、液限、塑性指数和液性指数等，易于测量、误差小且能批量测量。因此一些学者尝试通过建立土体常规物性指标与黄土湿陷性系数的关系，快速批量的对特定地区黄土湿陷性系数进行预测，取得了丰硕的成果。苏强[8]、舒志乐等[9]通过对黄土湿陷性系数和物性指标进行相关性分析，分别建立了黄土湿陷性系数与物性指标的一元和多元线性回归式；李萍等[6]采用多因素分析法建立了湿陷性系数与物性指标间的多元非线性回归式；邵生俊等[10]、徐志军等[11]采用因子分析法消除物性指标之间的共线性，建立了相关回归方程；井彦林等[12]采用最小二乘法支持向量机建立了黄土湿陷性系数预测模型；冯小东[13]采用反向传播(back propagation，BP)神经网络对黄土湿陷性进行预测；李瑞娥等[14]利用模糊信息优化技术建立了黄土湿陷性系数与物性指标间的模糊关系；马闫等[15]建立了黄土湿陷性系数径向基函数(radial basis function，RBF)神经网络预测模型；韩晓萌[16]采用自适应模糊神经网络利用物性指标对黄土湿陷性进行预测。

综上，虽然不少学者利用黄土基本物性指标建立了不同的黄土湿陷性系数单一预测模型，但单一模型都基于一定的假定，存在自身缺陷，所以精度难以提高。为此，基于4种不同单一预测模型，提出了离散型二项式系数组合模型，使单一模型间能够充分互补，预测精度大幅度提高。

1 预测模型原理

1.1 单一预测模型

1.1.1 多元线性回归

在科学研究中，当因变量y受到多个自变量xj(j=1,2,…，m)的影响时,可以采用多元线性回归对y进行预测[17]。多元线性回归基本模型为

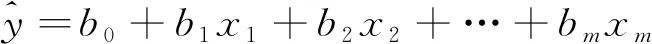
(1)

(2)

令

则式(2)可写为

(3)

式(1)表示m+1维空间中的平面，当m=2时为真正的平面，如图1所示。

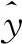
β=[b0,b1,b2, …，bm]T=(XTX)-1XTY

(4)

ei为第i组数据的回归误差；x1、x2为自变量图1 真实值与回归值示意图Fig.1 Schematic diagram of true value and regression value

1.1.2 BP神经网络

人工神经网络是基于拥有大量神经元结构的生物大脑建立的数据分析预测模型。其中由于BP神经网络具有容错率高、非线性映射和自学习适应等优点，是目前人工神经网络应用最广泛的一种[18]。BP神经网络由一个输入层、一个或多个隐含层和一个输出层组成，属于多层前馈神经网络，且误差反向传递即计算某一节点误差时需先求得与之相连的下一节点的误差值，因此误差必须自输出层开始计算。由于不同变量数据的数值大小存在一定差异性，为避免数值较大变量覆盖较小变量，需先将数据进行归一化处理[19]。

BP神经网络基本模型如图2所示，m个自变量xj(j=1,2,…,m)作为输入节点，因变量y作为输出节点。运用程序调整每个节点权值ω，进而得到输出值，将输出值与真实值进行对比分析，若精度未达到要求，需再次调整各节点权重ω，直至精度满足要求。

由Kolmogrov定理可知，一个由m个输入节点，s个输出节点和2m+1个隐含节点的3层BP神经网络可以精确的反映任何映射关系[19]，采用上述3层BP神经网络开展预测。

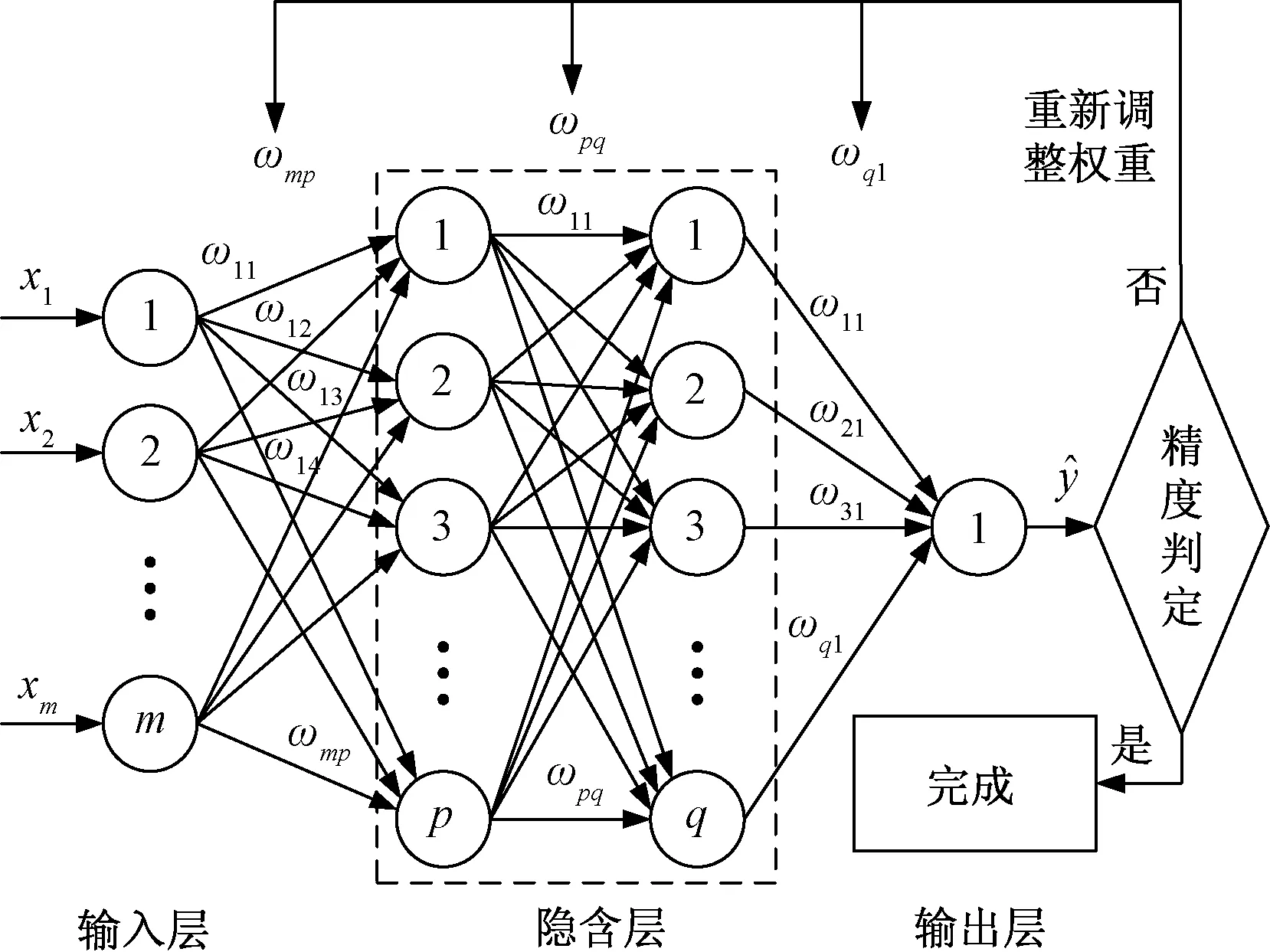
p为第一隐含层编号为p的节点；q为第二隐含层编号为q的节点；ωmp为编号为m的自变量与第一隐含层编号为p的节点之间的权重；ωpq为第一隐含层编号为p的节点与第二隐含层编号为q的节点之间的权重；ωq1为第二隐含层编号为q的节点与输出变量间的权重图2 BP神经网络流程图Fig.2 BP neural network flow chart

1.1.3 支持向量机回归

支持向量机(support vector machine,SVM)是基于结构风险最小化原则提出的统计学理论，其具有良好的泛化能力，可将问题转化为凸优化问题，使局部最优解即为全局最优解。如图3(a)所示，三角形和圆形分别代表了两类样本，支持向量机的原理为寻求一个既能保证两类样本无误的分隔开又能使分类间隔最大的最优超平面。对于样本非线性可分的情况，如图3(b)所示，可以运用非线性变换将样本映射到更高的维度中，再寻求最优超平面。

L为最优超平面；L1、L2分别为平行于L且经过各分类样本中距L最近的样本的平面图3 支持向量机示意图Fig.3 Support vector machine diagram

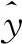
(4)

(5)

(6)

式中：υ为线性回归的斜率；x为自变量；b为线性回归的截距；min为求代数式的最小值。

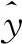
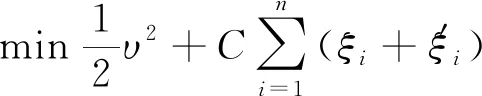
(7)

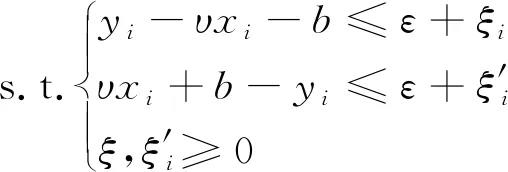
(8)

引入Lagrange乘子αi和α′i，以及利用KKT(Karush-Kuhn-Tucker conditions)条件可得到回归函数为[20]

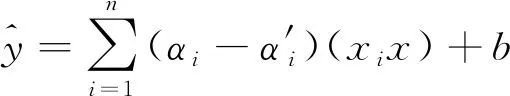
(9)

现实中大多数据是非线性可分的，因此需要进行非线性支持向量机回归。非线性支持向量机回归即先通过非线性映射Φ将数据映射到高维特征空间后再进行线性回归。通过核函数k(xi,xj)=Φ(xi)Φ(xj)来处理数据，不需要计算映射到高维空间数据坐标，避免了烦琐的点积运算。目前关于核函数的选取没有统一标准，一般认为高斯径向基核函数具有较好的稳定性，故选用高斯径向基核函数。非线性支持向量机回归的表达式为

(10)

1.1.4 随机森林回归

随机森林(random forest，RF)是一种基于决策树(分类树和回归树)的集成学习算法。由于其不易产生过拟合，泛化能力较强，对异常数据具有较好的鲁棒性，常用于处理分类和回归问题。随机森林回归原理如图4所示，运用bootstrap放回随机抽样法从原始训练集中抽取与原始训练集数据数量相等的训练子集，共抽取k组，用于训练k棵回归树模型。将预测集数据分别带入训练好的回归树模型得到k组回归值，再将k组预测集回归值取均值即为随机森林回归值[21]。

图4 随机森林回归原理Fig.4 Random forest regression principle

1.2 组合预测模型

组合预测模型就是将多种单一模型的预测结果，通过一定规则进行组合，以达到合理利用各单一模型预测结果，克服单一模型缺陷与误差的目的。若共有T个单一预测模型，n组训练样本，H组预测样本，则组合模型预测结果可表示为

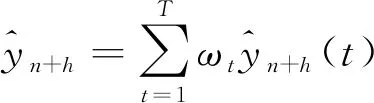
(11)

1.2.1 方差倒数法组合模型

方差倒数法组合模型原理为计算各单一预测模型训练集预测值与真实值的方差倒数，然后按方差倒数赋予各单一模型权重，方差越小赋予权重越高，权重的计算公式为

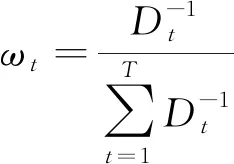
(12)

式(12)中：Dt为第t个单一预测模型训练集方差。

1.2.2 二项式系数法组合模型

二项式系数法组合模型是基于预测集预测结果赋予各模型权重。先求出各单一预测模型的H个预测样本的预测平均值,然后按均值从小到大对模型增序排列，再利用二项式系数赋予权重，使均值排序越靠近中间位置的模型权重越大，权重的计算公式为[22]

(13)

1.2.3 离散型二次项系数法组合模型

二项式系数法组合模型虽能使预测集的预测值靠近整体预测均值排序居中的单一预测模型的预测值，但预测集各模型整体预测均值排序与单个预测样本预测值排序并不完全相同，甚至相反。这就可能使某一预测样本的组合预测值更靠近最大值或最小值，而不是排序居中的预测值。因此，针对这一问题提出了离散型二项式系数法组合模型，该方法即对每一个预测样本的各单一模型预测值进行增序排列，并用二项式系数赋予权重，以保证每一个预测样本的组合预测值都能靠近该预测样本单一模型预测值增序排列的中间值，第h个预测样本的预测值增序排列第t位的单一预测模型权重计算公式为

(14)

式(14)中：ωt,h为第h个预测样本的预测值增序排列第t位的单一预测模型权重，h=1,2,…，H。

2 建立数据库及预测模型的算法实现

2.1 数据库的创建

利用在陕西省“引汉济渭”工程中收集到的60组湿陷性黄土相关数据[23]，建立了湿陷性黄土物性指标数据库，包括湿陷性系数、干密度、孔隙比、天然含水量、饱和度、塑限、液限、塑性指数和液性指数等。数据库前50组作为训练集，通过训练得到该地区利用黄土物性指标预测湿陷性系数的预测模型。后10组数据作为预测集，用来验证预测模型的可行性与准确性。

2.2 离散型二项式系数组合模型的算法实现

黄土湿陷性系数预测模型利用MATLAB编程实现，如图5所示。具体步骤如下。

图5 预测模型MATLAB算法实现流程Fig.5 MATLAB algorithm implementation process of prediction model

步骤1导入数据库前50组数据计算相关系数表，并结合随机森林重要性指数排序综合确定拟用物性指标。

δs为湿陷性系数；ρd为干密度；e为孔隙比；ω为天然含水量；Sr为饱和度；wL为液限；wP为塑限；IP为塑性指数；IL为液性指数图6 各物性指标间相关系数及散点图Fig.6 Correlation coefficients and scatter plots among various physical properties

步骤2导入已确定物性指标相关数据，运用多元线性回归得到单一预测模型1，将导入数据进行归一化处理，先后进行支持向量机回归(SVR)、BP神经网络预测和RF回归，得到单一预测模型2、3和4。

步骤3将后10组数据导入各单一预测模型，得到4种单一模型预测结果，再分别运用方差倒数法、二项式系数法和离散型二项式系数法计算模型权重，得到3种组合模型预测结果。

3 黄土物性指标的选取

3.1 相关系数法

相关系数R表示两变量的相关程度，计算如式(15)所示， 且|R|≤1，|R|越接近1，相关性越大[17]。

(15)

为了选择合适的物性指标，首先计算各物性指标间的相关系数进行相关性分析，如图6所示。上三角为各物性指标间的相关系数，下三角为对应的散点图，对角线为各物性指标的频率分布直方图。易见湿陷性系数δs与各物性指标相关性排序为:饱和度Sr>干密度ρd>孔隙比e>液性指数IL>天然含水量ω>塑性指数IP>液限wL>塑限wP，又由于干密度与孔隙比相关性接近1(0.986)，故两者取其中之一(干密度)分析即可。而塑性指数、液限和塑限与湿陷性系数的相关系数均小于0.15，相关性很差，因此不参与预测。按照相关系数法选取饱和度、干密度、液性指数和天然含水量作为预测物性指标。

3.2 随机森林重要性指数法

随机森林不仅能够用于分类与回归，还可进行变量重要性分析，得到各因变量的重要性指数。如前文所述，随机森林回归在采用bootstrap抽样方法时，若原始训练集有n个样本，则在某一子训练集的抽取中，每个样本未被抽中的概率均为(1-1/n)n，当n为50时，概率约为36.4%，这部分未被抽中的样本称为袋外(out of bag, OOB)数据。将每棵树的袋外数据带入与之相对应的回归树可得到袋外误差errOOB1。然后对袋外数据的某一因变量xi施加噪声干扰(即改变其数值)，得到干扰后袋外误差errOOB2。依次计算出k棵回归树的errOOB1和errOOB2，代入随机森林重要性指数(feature importance measures, FIM)计算公式[式(16)]，计算结果如图7所示。

(16)

由图7可见，重要性排序前五的物性指标与相关系数法相同，故按照随机森林重要性指数法也选取饱和度、干密度、液性指数和天然含水量作为预测物性指标。

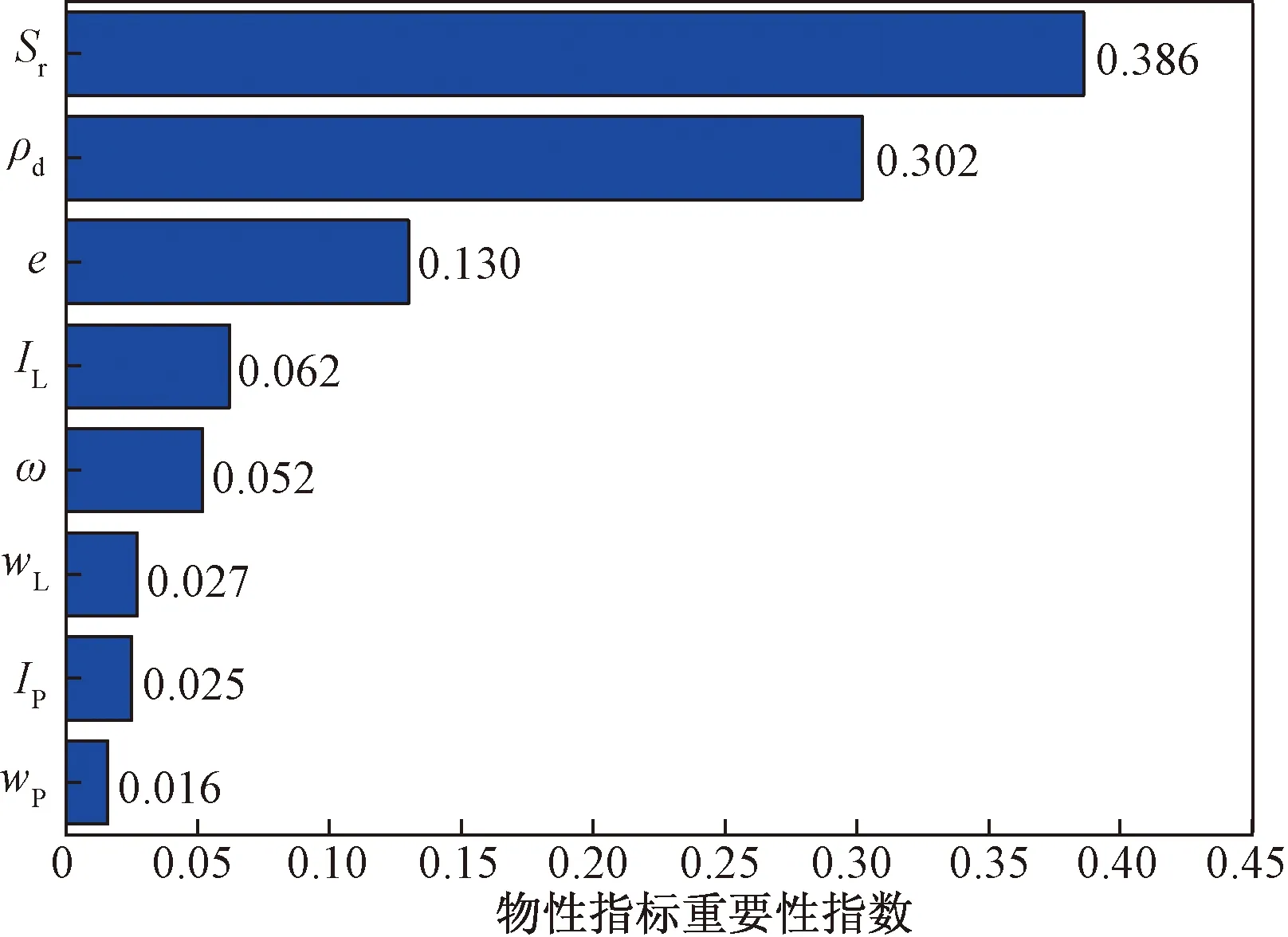
图7 随机森林重要性指数Fig.7 Random Forest importance exponent

3.3 选取物性指标数据

综合相关系数与随机森林重要性指数，选取饱和度Sr、干密度ρd(单位：g/cm3)、液性指数IL和天然含水量ω(单位：%)4种物性指标构建黄土湿陷性系数δs预测模型。训练集(1～50)与测试集(51～60)相关数据如表1所示。

4 预测结果与精度分析

4.1 预测结果

将表1数据导入前文编写的MATLAB程序中，可分别得到多元线性回归(模型1)、BP神经网络(模型2)、SVR(模型3)、RF回归(模型4)、方差倒数法组合模型(模型5)、二项式系数法组合模型(模型6)和离散型二项式系数法组合模型(模型7)的预测集预测值如表2所示。上述4种单一模型和3种组合模型预测曲线如图8所示。

表1 训练集与预测集样本数据

表2 各预测模型预测集湿陷性系数预测值

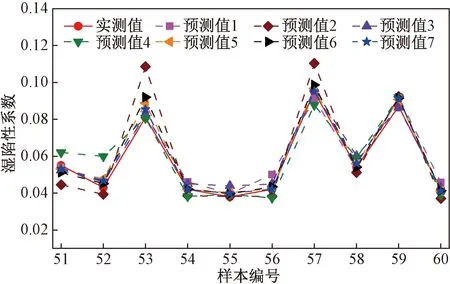
图8 各模型预测曲线Fig.8 Each model prediction curve

4.2 模型预测精度分析

为了更清晰的分析图8的预测结果，分别绘制了各预测模型相对误差图及残差图，如图9、图10所示。由图9可知，4种单一模型(模型1～模型4)的最大相对误差均超过15%，甚至将近40%，传统组合模型(模型5和模型6)最大相对误差均位于10%～15%，而所提出的组合预测模型(模型7)最大相对误差小于10%，为8.98%。由图10可知，四种单一模型(模型1～模型4)以及模型5的最大残差均大于0.05，模型6和模型7的最大残差均小于0.05，且模型7最大残差最小。

图9 模型预测相对误差Fig.9 Relative error of model prediction

图10 各模型预测残差Fig.10 Model prediction residuals

此外，选用绝对误差平方和(the sum of squares due to error，SSE)、标准误差(standard error, SE)、相对误差平方和(the sum of squares due to relative error, SSRE)、相对标准误差(standard relative error, SRE)、平均绝对百分误差(mean absolute percentage error, MAPE)和希尔不等系数(Theil inequality coefficient, Theil IC)精度判定指标开展模型精度分析。精度指标计算公式如式(17)所示，精度指标数值越小，模型精度越高，7种模型精度指标计算结果如表3所示。由表3可知，4种单一预测模型中模型1和3精度指标均优于模型2和4。对比单一模型与组合模型精度指标，可见组合模型精度指标整体优于单一模型精度指标，此外所提出的组合预测模型(模型7)所有精度指标相对于其他模型均为最优。

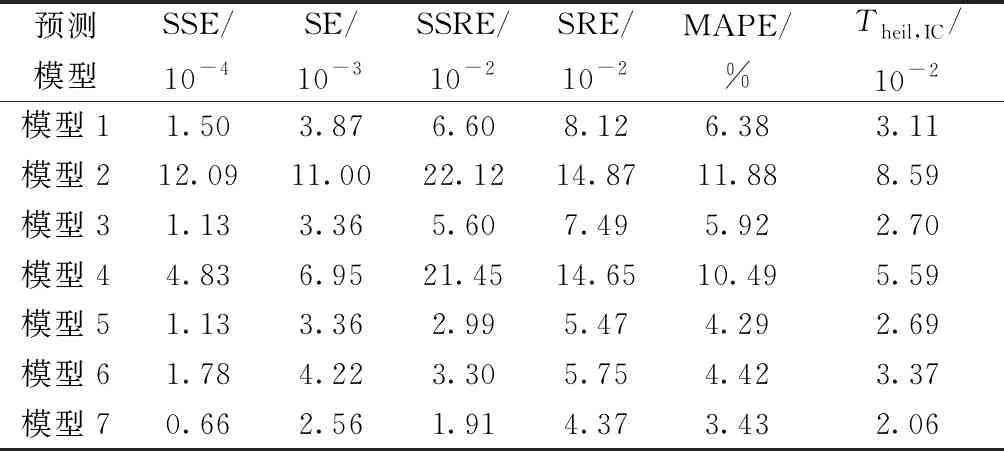
表3 模型预测精度指标对比

(17)

综合图9、图10和表3的分析结果可知，3种组合预测模型预测精度整体高于4种单一预测模型。这是由于组合模型能够对各单一模型进行模型互补，在某一样本点即使某一单一预测模型有较大误差，组合模型也可以利用其他单一模型给予弥补。本文提出的离散型二项式系数法组合预测模型(模型7)各指标均最小，预测精度最高，是因为该方法能够先大致判断在某一样本处4种单一模型预测偏差大小，然后基于偏差大小赋予模型不同权重，偏离平均值越大赋予权重越小，以使组合预测结果偏差尽可能小，大大提高预测精度。

5 结论

黄土湿陷性系数是湿陷性黄土地区工程设计中的必要参数。通过创建黄土湿陷性系数及其物性指标数据库，采用MATLAB数据分析软件建立了4种单一预测模型、2种传统组合预测模型和1种新型组合预测模型，并进行精度分析，得出如下主要结论。

(1)采用相关系数和随机森林重要性指数综合判定该地区物性指标对湿陷性系数的重要性，从大到小依次为饱和度、干密度、孔隙比、液性指数、天然含水量、塑性指数、液限和塑限，并选取饱和度、干密度、液性指数和天然含水量4种物性指标来开展黄土湿陷性系数预测。

(2)提出一套新型组合模型算法(离散型二项式系数法组合模型)，所提模型能够使预测值尽可能地靠近每个样本排序居中的单一模型预测值，以达到模型互补提高预测精度的目的。

(3)利用SSE、SE、SSRE、SRE、MAPE和Theil，IC6种精度指标及相对误差和残差图对4种单一预测模型、2种传统组合预测模型和所提出的新型组合预测模型进行精度分析，发现组合预测模型精度整体高于单一预测模型，且所提出的新型预测模型各精度指标均最小，精度最高，最大相对误差为8.98%，平均相对误差为3.43%。