基于捷联惯导的蛇形管道机器人定位算法

张成林， 王亚慧， 张秋逸

(北京建筑大学电气与信息工程学院， 北京 100044)

自进入21世纪以来，中国城市化速度大大加快，导致燃气管网的覆盖率与使用范围大大提高，燃气管道的安全性将直接决定着城市是否能够安全稳定的运行[1]。为了检查与维护燃气管道，邓蕊等[2]、邢利辉等[3]设计了一种蛇形管道探测机器人，该机器人以14节舵机连接而成，可进行行波、蜿蜒、螺旋等运动，当机器人发现安全隐患和损伤后需要将位置信息回馈给地面上的工作人员，以方便进行定点挖掘和管道维护，为此蛇形管道探测机器人定位系统的准确与否尤为重要。

燃气管道通常被掩埋于地下，目前应用于地下导航定位的技术主要有射频识别技术(radio frequency identification，RFID)、无线网络协议定位技术(ZigBee)、无线相容认证技术(wireless fidelity，WIFI)、超宽带定位技术(ultra-wideband，UWB)及捷联式惯性导航定位系统(strapdown inertial navigation system，SINS)技术等[4-6]。Zhang等[7]使用动态主动射频识别标定系统的射频识别定位技术，该定位技术使用4个电子读取仪器、4个相邻及28个用于参考的标签，建立了一个改进的LANDMARC算法获得理想的地下定位效果。但是阅读器在接收射频识别信息时，由于参考标签数量的增加而产生信号冲突，产生冲突的信号强度指示(received signal strength indicator，RSSI)增加了系统的复杂性，使得定位时间大大增加。Zhou等[8]提出了一种基于RSSI值的ZigBee网络测距定位技术。经过平均模型滤波和高斯滤波模型处理，得到RSSI范围。但是基于RSSI值的ZigBee测距定位技术方法只能在一些简单的环境中使用，对于地下管道这种可能有脏物、裂缝的场景可靠度不高。李刘颂等[9]提出了一种基于行人走路时识别姿态变化的惯导算法, 使用惯性测量器件(inertial measurement unit，IMU)采集人行走时的加速度和角速度数据, 根据该算法计算结果建立了行人的步长模型，在保证单步位移较高精度的前提下准确估计了行人的位移情况。但是该算法并未加入误差补偿，长时间进行定位会导致误差逐渐积累无法获得准确地位置信息。郭梁等[10]提出了一种基于捷联惯性导航的矿用单轨吊机车定位算法。利用限幅滤波和去零偏等预处理等方法对数据处理，方向余弦矩阵法消除重力分量对数据的干扰，利用加速度变化率阈值法和零速修正法修正稳态误差，实现了吊车的精确定位。但是未对机车急停时的加速度误差进行分析。

针对上述存在的问题，为了能够在无法接收卫星导航信号的地下管道内对蛇形管道机器人精确定位。采用完全自式的导航定位方法，即捷联式惯性导航定位算法，在不接收任何外部信号的情况下实现定位功能。利用mpu9250九轴惯性单元采集蛇形机器人的加速度、角速度信息。通过四元数法构造并更新姿态矩阵，对系统和元器件造成的定位误差进行分析并建模，融合卡尔曼滤波算法进行误差补偿。为了验证定位算法的可靠性，利用本课题组自主开发设计的蛇形机器人携带惯性器件进行数据采集，发现解算后的定位效果满足实际需求，为蛇形机器人在地下管道内部定位研究提供科学参考依据。

1 捷联式惯性导航系统常用坐标系

参考坐标系是标定物体位置的重要参照，因此坐标系是捷联式惯性导航的基础，SINS经典坐标系，如图1所示。

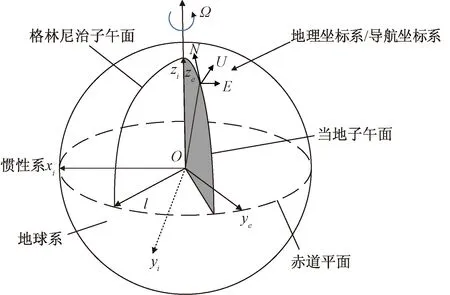
Ω为地球自转角速率；l为赤道线；O点为地心； N、E、U分别为东、北、天3个方向图1 惯性导航常用坐标系Fig.1 Inertial navigation common coordinate system

(1)地心坐标系(简称i系)，i系采用地心O作为其坐标系的原点，xi轴和yi轴相互垂直且位于地球的赤道面内，zi轴垂直于xi轴和yi轴形成的平面，且以北极为zi轴的正向，其坐标系方向并不随地球的自转而转动。

(2)地球坐标系(简称e系)，e系同i系相似，均采用地心O作为其坐标系的原点，xe轴和ye形成的平面与地球的赤道面重叠，xe轴指向格林威治子午线方向，e系以地球的自转轴作为ze轴，随着地球自转轴而动。

(3)导航坐标系(简称n系)，以相关载体重心O为坐标系原点，以载体的东向为xn轴、以载体的北向为xn轴、以天为xz轴，因此n系也称为东北天坐标系[11]。

(4)载体坐标系(简称b系)，b系与载体相连，将载体重心设为坐标系原点，xb轴为载体呈直线时正前方，yb轴指向载体的侧方位，zb轴指向载体并向上。

2 定位系统算法设计

2.1 捷联惯导算法

SINS摒弃笨重的物理平台，以牛顿力学定律为基础，采用加速度计和陀螺仪直接固联在被测物体上的方式，通过加速度传感器和陀螺仪实时采集线加速度和角加速度数据，融合卡尔曼滤波算法，根据惯性微分方程, 可对线加速度进行二次积分得到目标物体的位移[12]。利用陀螺仪测得载体在相对惯性空间下3个方向的角速度信息，经过坐标变换，最终算出其姿态信息。SINS的原理如图2所示。

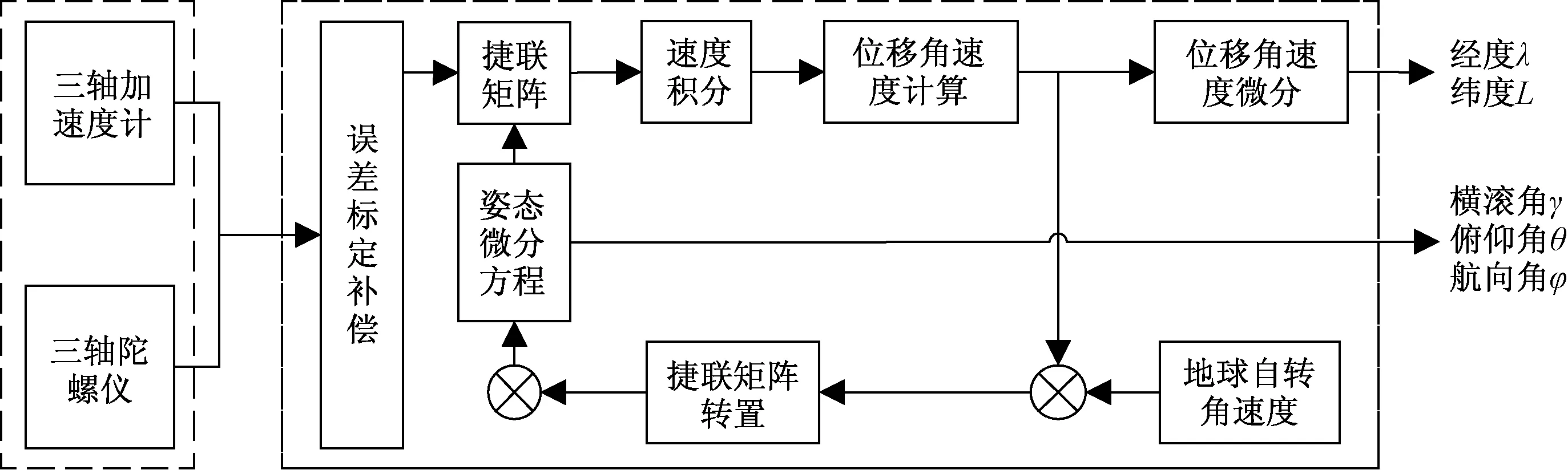
图2 捷联惯导原理图Fig.2 SINS schematic diagram

SINS中最关键的步骤为姿态矩阵的求解，姿态矩阵包含被测物体的位姿和速度等信息，因此被求解的姿态矩阵越逼近真实的姿态矩阵，求解的位置信息就越精准。SINS的误差主要来源于惯性器件，包括刻度因子误差、安装误差、零偏误差及随机误差等。此外，从加速度得到位置信息，需经两次积分运算，但是积分运算会将误差放大，因此引入卡尔曼滤波算法并将其融合蛇形机器人的加速度及角速度信息，有效的补偿惯导误差。

2.2 卡尔曼滤波误差补偿

卡尔曼滤波算法首先需要确定误差模型，推导出误差模型后再由卡尔曼滤波进行最优估计，卡尔曼滤波算法流程图如图3所示。其中误差模型包含元件及系统误差两种，元件误差包括加速度计误差和陀螺仪误差，系统误差包括姿态误差、速度误差及位置误差。

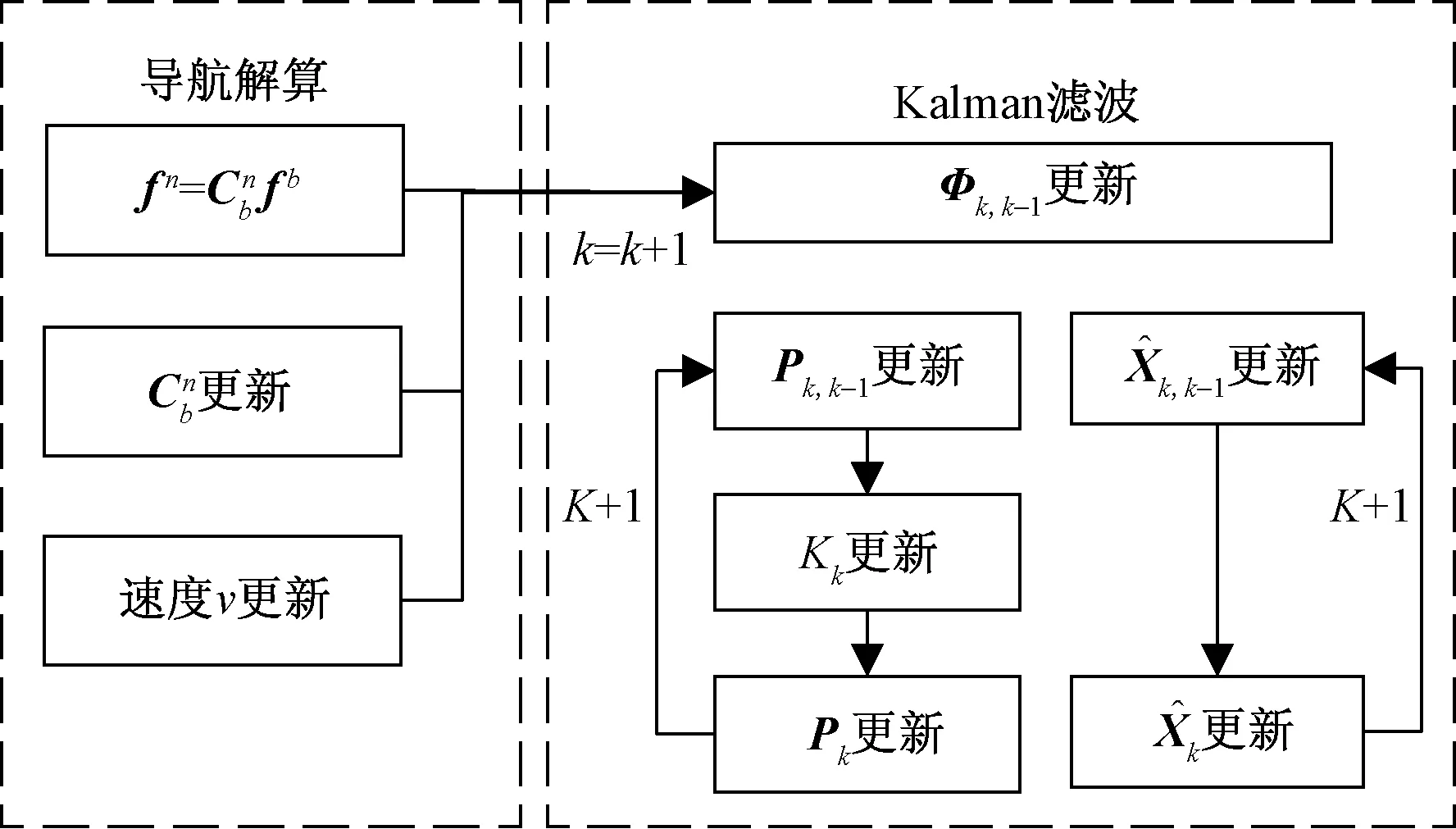
k为时间；K为卡尔曼滤波增益加权因子；Kk为卡尔曼滤波增益矩阵；fb为加速度计输出比力；fn为比力在导航坐标系中的投影；为姿态转换矩阵；为k时刻系统状态；为系统上一时刻预测状态值；Pk为状态对应的协方差矩阵；Pk,k-1为状态对应的协方差矩阵；Φk,k-1为系统矩阵图3 卡尔曼滤波算法误差补偿流程Fig.3 Error compensation process of Kalman filter algorithm

陀螺仪误差主要包括刻度因数误差、随机常数误差、一阶马尔可夫过程误差、白噪声，经分析可以推导出陀螺仪误差模型为

(1)

加速度计误差与陀螺仪误差相似，通过分析可推导出加速度计误差为

(2)

蛇形机器人未启动时为静止状态，因此是静基座下的初始对准，在静基座的前提下可以认为失准角为小角度失准角甚至角度为0°，则可得到精对准误差模型为

(3)

式(3)中：ΔVE为东向误差；ΔVN为北向误差；φN、φE、φU分别为东、北、天3个方向的姿态误差角；ωie为地球自转角速率；g为重力加速度；L为纬度；ωie为地球自转角速率；φE、φN、φU分别为东、北、天3个方向上的姿态误差角；∇x为加速度计零偏在数学平台x轴的投影；∇y为加速度计零偏在数学平台y轴的投影；ΔL为纬度误差；R为地球半径；εE、εN、εU分别为陀螺仪东、北、天方向的陀螺漂移误差。

IMU元件的偏置误差及漂移误差默认为常数，再以东、北、天坐标系为导航坐标系的前提下，则有

(4)

式(4)中：∇E为加速度计东向偏置误差；∇N为加速度计北向偏置误差；∇U为加速度计天向偏置误差；∇x、∇y、∇z分别为载体坐标系3个轴向上的加速度计偏执误差；εx、εy、εz分别为载体坐标系3个轴向上的脱落漂移误差。

则可得误差状态方程为

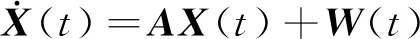
(5)

式(5)中:X(t)为系统状态向量；A为状态转移矩阵；W(t)为高斯白噪声。

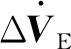
Z(t)=HX(t)+V(t)

(6)

式(6)中：Z(t)为量测矩阵；H为常值矩阵；V(t)为随机噪声。

式(5)、式(6)的离散形式为

Xk=Φk,k-1Xk-1+Γk,k-1Wk-1

(7)

Zk=HkXk+Vk

(8)

式中：Γk,k-1为噪声驱动矩阵；Wk-1为过程白噪声；Xk为k时刻系统状态量；Zk为k时刻系统的观测量；Vk为系统量测噪声矩阵。

Φk,k-1和Γk,k-1可表示为

(9)

式(9)中：T为卡尔曼滤波的时间周期；I为单位阵；G为常量矩阵；Ak-1为前一时刻的系统矩阵。

在tk时刻，量测噪声矩阵Vk和激励噪声矩阵Wk互不相关且为零均值的白噪声矩阵，则可得到系统噪声方差矩阵Qk和量测噪声方差矩阵Rk，可表示为

(10)

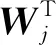
将求出的Qk、Rk、Φk,k-1、Γk,k-1及量测矩阵代入卡尔曼滤波即可。

2.3 四阶龙格-库塔法求解四元数微分方程

导航坐标系Oxnynzn分别绕zn轴、xn轴、yn的顺序旋转三次可得到载体坐标系Oxbybzb，则从导航坐标系转换到载体坐标系的矩阵运算可表示为

(11)

四元数法具有计算量小、精度高、避免产生奇点等优势。四元数Q是包括一个实部3个虚部的超复数，刚体沿着以时变矢量，旋转一定的角度[13]，用转角表示四元数的首项，旋转的方向由后三项表示，q0、q1、q2、q3为实数，i、j、k为相互正交的单位矢量，其定义为

Q=q0+q1i+q2j+q3k

(12)

龙格-库塔法是一种具有高精度微分方程的数值解法[14-16]。龙格-塔库算法采用在积分区间内插值的方式，平滑总斜率。插值越多，得到的结果就越精确，但是工作量也会随之大大提高。四阶龙格-塔库算法在解算四元数微分方程上，不仅求解结果精准，而且计算量也较少。其原理为

(13)

式(13)中：K1为初始时刻斜率；K2、K3为中间两点斜率；K4为该段时间终点的斜率；τ为计算周期。

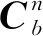
(14)

从式(14)中可以看出，四元数对应姿态矩阵中的不同元素，因此，可以通过四元数解算出姿态更新矩阵及导航信息。其相应的姿态信息可表示为

(15)

式(15)中：θ为载体的俯仰角；γ为载体的横滚角；φ为载体的航向角。

捷联惯导算法的速度微分方程为

(16)

位置更新方程为

(17)

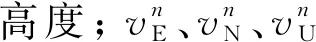
此时根据前一刻载体信息得到当前时刻载体位置信息。

3 实验及结果分析

为了验证蛇形管道探测机器人定位子系统算法的可行性，搭建了包括蛇形管道探测机器人、直流稳压电源、笔记本电脑、示波器、惯导芯片等实验器材的实验平台。

实验数据采集对惯性传感器的精度提出了较高要求，本实验采用的MPU9250惯性传感器有3个16位加速度AD输出，3个16位陀螺仪AD输出，3个16位磁力计AD输出。较MPU6250传感器多了三轴磁力计，z轴航向角融合磁力传感器滤波，可以减小漂移误差，稳定航向角度数据。能够进行精密的慢速和快速运动跟踪。

实验基于蛇形管道探测机器人的行波运动进行测量分析。惯性传感器采样间隔为0.1 s，一共采样67 s，蛇形机器人一共行走了512.54 cm，以平均每秒7.65 cm的速度向正北方向进行行波运动。蛇形机器人的机械结构由14个舵机首尾依次连接而成，将MPU9250传感器安装在蛇形机器人的第6个舵机上进行加速度及角速度信息采集。截取惯性传感器在采集数据时蛇形机器人的部分运动姿态效果如图4所示。

根据IMU器件采集到的数据，可以得到加速度、角速度及角度时域波形如图5所示。

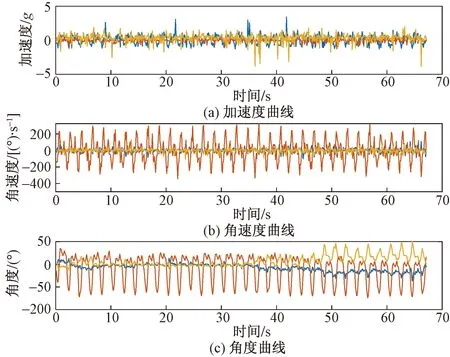
图5 惯性传感器输出数据时域波形图Fig.5 Time domain waveform of IMU output data

蛇形机器人通过偶数位舵机上下摆动来拖带动奇数位舵机，带动整体在正北方向呈直线向前运动。经上述算法解算后利用MATLAB仿真软件的到蛇形机器人在东、北、天3个方向上速度及位移的波形图如图6所示。

图6 解算后的蛇形机器人速度及移变化曲线图Fig.6 Velocity and displacement curve of snake robot after solution

本实验在透明管道内进行，管壁底部呈U形，所以在行波运动的过程中会出现轻微的侧滑现象，从图6可以看出，蛇形机器人在x轴方向，即东西两向最大位移在1 cm左右。z轴方向，即天向呈规律的上下运动，最大位移不超过15 cm。

y轴方向，即北向，蛇形机器人的主要位移方向上的位移距离经算法解算后与实际位移对比得出的误差如表1所示。

实验过程中每隔5 s准确记录一次蛇形机器人的位移距离，与算法解算出的位移进行对比，捷联式惯性导航算法随着时间变长会导致误差不断累积，从表1中可以看出,定位误差随着时间的变化会逐渐增大，67 s内蛇形机器人共行走512.54 cm，实验过程记录最大误差20.51 cm，误差率为4%。最大误差率出现在第55秒，误差率为4.7%，本实验误差率在30 s之后逐步收敛至4%～5%，证明卡尔曼滤波算法确实起到了误差补偿作用。

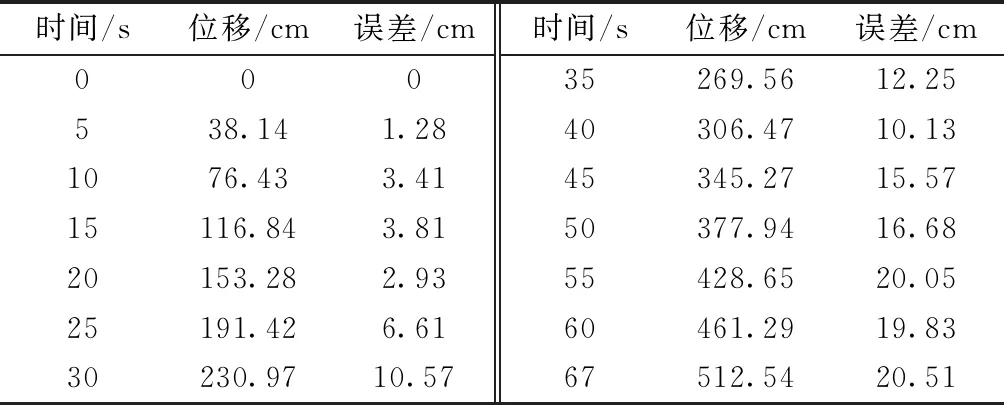
表1 蛇形机器人实际位移及误差Table 1 Actual displacement and error of snake robot

4 结论

基于捷联式惯性导航算法，初步为蛇形管道探测机器人设计了一种适用于地下管道内的定位导航算法。为了更有利于观测蛇形机器人实际的位移，方便与算法解算得到的结果做比较，实验在透明的玻璃管道内进行，得出如下结论。

(1)通过不同算法的对比与可行性分析，设计了可应用于蛇形管道探测机器人的捷联惯导定位方法。该方法通过九轴惯性传感器采集加速度和角速度数据，采用卡尔诺曼滤波算法融合数据、四元数龙格-库塔算法解算微分方程，大大降低了定位误差和计算量。

(2)搭建了实验平台，实验结果表明该定位系统能够在难以接受外界信号的地下管道内，为机器人精确的定位信息。相比于人工查探损伤位置更具安全性、经济性和准确性。为地下管道内定位提供一种新的思路。