基于混沌天牛群算法优化的神经网络分类模型

王丽， 陈基漓,2*， 谢晓兰,2， 徐荣安

(1.桂林理工大学信息科学与工程学院， 桂林 514004； 2.广西嵌入式技术与智能系统重点实验室， 桂林 514004)

随着大数据时代的快速发展，人们对于获取的数据要求越来越高，越来越多的学者专注于如何从海量的数据中提取有效信息并将其进行分类处理。经典的分类模型有很多，常见的有支持向量机(support vector machine, SVM)、K近邻(K-nearest neighbor, KNN)、决策树和神经网络分类模型，学者们通过对这些分类模型的研究，提出了各种优化方法，如利用智能算法优化SVM[1-2]，多种分类模型组合分类[3]、动态分类[4-5]等。传统的反向传播 (back-propagation，BP)神经网络[6]是一种多层前馈神经网络，由于BP神经网络的权值和阈值[7]是初始化时随机生成的，导致BP神经网络在训练时易陷入局部最优，其稳定性较差等问题。为了克服这些缺点，许多学者在BP神经网络中引入群智能算法对其进行改进。Xu等[8]采用人工蜂群算法 (artificial bee colony, ABC)优化BP神经网络后对磁流变阻尼器进行半主动控制，提高了算法的计算效率和精度；李琪等[9]利用粒子群优化算法(particle swarm optimization，PSO)优化BP神经网络，根据实际工况建立PSO-BP钻井机械钻速预测模型并进行模型评价，结果表明该模型具有良好的预测精度。但是它们存在许多缺点，如ABC算法局部搜索能力弱，算法性能受种群数量和limit控制参数影响较大；PSO算法寻优精度低，在迭代后期无法保持种群的多样性，从而陷入局部最优。

Jiang等[10]提出了基于天牛搜寻食物原理的天牛须搜索(beetle antennae search，BAS) 算法。天牛须搜索算法与粒子群优化算法、遗传算法(genetic algorithm，GA)等都是元启发式智能优化算法，PSO和GA通过种群寻优，而BAS算法在寻优过程中只有一个天牛个体，BAS 算法简单，参数少，容易实现，不会被过多的初始条件所约束，并且适用于求解更为复杂的非线性优化问题。Fan等[11]将BAS算法与比例-积分-微分(proportion integral differential，PID)策略相结合，设计了BAS-PID控制器，大大提高了电液位置伺服控制系统的性能，有效抑制了系统的干扰信号；赵辉等[12]提出了将A*算法与BAS算法相结合的BAS-A*全局规划方法，用于农业机器人的路径规划，在缩短路径长度和降低累计转折点数量方面验证了所提方法的有效性。Cai等[13]利用BAS良好的初始参数加快Elman神经网络训练，建立BAS-Elman神经网络模型，验证了该模型应用于隧道工程爆破震动速度预测的可行性。然而，标准的天牛须搜索算法仍存在局部搜索能力不够理想，且单个个体搜索极易在迭代过程中陷入局部最优，不能找到全局最优值的问题，因此，BAS算法的寻优精度还有一定的提升空间。

针对BP神经网络和天牛须搜索算法的缺点，提出一种改进天牛须搜索算法优化的BP神经网络分类模型，利用优化后的IBAS算法得到的最优解作为BP神经网络的权阈值进行分类训练。基于此，以改进的天牛须搜索及反向传播神经网络(improved beetle antennae search and back propagation neural network，IBAS-BPNN)分类模型的分类正确率最佳为优化目标，与其他6种分类模型比较多个数据集的分类效果，验证分类模型的有效性和准确性。

1 相关方法

1.1 BP神经网络

BP神经网络模型简单，在网络性能和理论方面都已经十分成熟，因此常被用于各种预测模型中。BP神经网络模型拓扑结构包括三个层次，分别是输入层、隐含层和输出层[14]，该网络的主要特点是信号正向传播，误差反向传播，这也是BP神经网络的学习过程。非线性映射是BP神经网络重要的能力，可以使映射关系之间不需要用数学方程来表示，BP神经网络中可以存储和学习大量的输入-输出对，只要为BP神经网络提供足够的样本进行训练和学习，就能够完整地描述输入空间到输出空间的非线性转换。典型的BP神经网络结构如图1[15]所示。

在BP神经网络中，输入层神经元的个数为输入样本数据的维数，即样本的属性个数；输出层神经元个数为预测的节点数，即输出的标签数；采用单层隐含层，隐含层神经元个数依据式(1)[16]得到范围，再通过比较不同个数的网络收敛误差来确定。

(1)

式(1)中：I为输入层神经元个数；H为隐含层神经元个数；O为输出层神经元个数；a为[0,10]之间的整数。

搜索算法的空间维度为

K=IH+HO+H+O

(2)

在BP神经网络进行训练之前，随机初始化网络的权阈值，开始进入正向传播阶段。在正向传播过程中，输入层的各个神经元接收需要处理的信息，并将其传送给隐含层，隐含层的各个神经元则负责处理这些信息，将处理后的信息传送给输出层，输出层则把处理结果输出给外界；计算输出值与实际值之间的误差，如果误差不满足精度要求，则进入误差反向传播阶段。在误差反向传播阶段，利用梯度下降法不断修正各层连接的权值和阈值，将误差从输出层转移回到隐含层和输出层的过程。循环往复这个过程，直到BP神经网络训练次数达到预设的最大迭代次数或输出的误差降低到目标值为止。

1.2 天牛须搜索算法

天牛须搜索算法的原理[17]：当天牛在寻找食物时，并不能清楚地知道食物具体所处位置，这时，食物的气味就相当于一个函数，天牛根据左右触角所接收的食物气味的强弱来确定搜索方向，即天牛的左右触角可以采集自身附近两点的气味值。如果天牛右边触角接收到的气味强度大于左边，则天牛下一步就会朝右飞去寻找食物，反之则朝左飞，最终找到全局气味最大点，就可以有效的找到食物。

在BAS 算法中，由于天牛个体的触须有着敏锐的感知能力，可以使该个体快速确定下一步的移动方向，不会无规则的盲目地移动，不仅降低了算法运算量，还提高算法收敛速度，从而达到寻找最优解的目的[18]。BAS算法流程如下。

步骤1随机地确定一个天牛须朝向作为搜索方向，确定算法的空间维度K。

(3)

式(3)中：dir为初始单位向量，表示天牛朝向；rand(K,1)为随机函数;K为空间维度。

步骤2初始化天牛坐标及其初始位置的适应度值，天牛质心的初始坐标由[-1,1]的随机数组成。

步骤3确定天牛左右触须在空间中的坐标位置。

(4)

式(4)中：t为迭代次数，t=0,1,…,N，其中N为最大迭代次数；d0为天牛左右须之间的距离；xt、xleft和xright分别为天牛在第t次迭代时天牛质心的坐标、天牛左边触须的位置坐标、天牛右边触须的位置坐标。

步骤4计算天牛左右触须的适应度值。f(·)函数为适应度函数，即计算f(xleft)和f(xright)的气味强度。

(5)

式(5)中：f(xleft)为天牛左边触须的适应度值；f(xright)为天牛右边触须的适应度值。

步骤5迭代更新天牛的位置。

xt+1=xt-Stdirsigh[f(xleft)-f(xright)]

(6)

式(6)中：St为第t次迭代时天牛行进的步长；sign(·)为符号函数。

1.3 SMOTE过采样

SMOTE[19]算法是基于随机过采样算法的一种改进方案，它的基本思想是分析少数类样本信息，采用随机线性插值的方法在近邻少数类样本之间手动增加新的少数类样本个数，再将合成的新样本添加到数据集中，从而达到数据平衡的状态，SMOTE算法步骤如下。

步骤1利用欧氏距离计算少数类中的每一个样本到该类中其他所有少数类样本之间的距离，得到k个近邻，按正序排列，一般k的取值为5。

步骤2根据少数样本与多数样本间的不平衡比设置采用倍率N。对于每一个少数类样本x，从其K近邻中随机选择xn个样本进行随机线性插值，构造新的少数类样本。线性插值计算公式为

xnew=x+rand(0,1)|x-xn|

(7)

式(7)中：xnew为生成的新样本。

步骤3将新生成的样本与原始训练集合并，产生新的训练集。

2 IBAS-BPNN分类模型

2.1 IBAS算法

2.1.1 天牛种群寻优

标准天牛须搜索算法中，只有一个天牛个体寻优，因此算法收敛速度快，但在更为复杂的函数优化问题中，由于每次迭代天牛个体都是随机的朝着某个方向移动，不能保证每次天牛位置更新后它的适应度值更优，且BAS的搜索空间存在一定的局限性，寻优精度就会大大降低，算法性能下降，不易找到最优解。因此，采用天牛种群进行寻优，通过使用n只天牛同时朝n个方向进行移动，可以扩大算法的搜索空间，从而可以提高算法在复杂空间中的寻优能力，增加天牛找到更优位置的可能性。天牛种群可以用矩阵表示为

X=[x1，x2，…，xn]T

(8)

xi=[xi,1,xi,2,…,xi,k]

(9)

式中：xi中的每个值表示每只天牛对应的问题维度，i=0,1,…,n，n为天牛的种群规模；K为问题维度。对应的天牛适应度值可表示为

FX=[fx1,fx2,…,fxn]T

(10)

fxi=[fxi,1,fxi,2,…,fxi,K]

(11)

式中：FX中的每个值表示n只天牛对应的适应度值；fxi中的每个值表示每只天牛对应的问题维度的适应度值。

2.1.2 Logistic混沌映射

随着迭代次数的增加，天牛个体的多样性将会逐渐减少，到迭代后期，算法易陷入局部最优。而混沌搜索能够以一定的规律不重复地遍历所有状态，其搜索能力优于随机搜索。采用Logistic混沌扰动机制优化算法，以其遍历全局的优点对种群进行混沌优化，使得天牛能够跳出局部最优，提高算法全局搜索能力和寻优精度。Logistic混沌映射表达式为

Xt+1=Xtμ(1-Xt)

(12)

式(12)中：μ为Logistic的控制参数，μ∈[0,4]；t为迭代次数；Xt为天牛在第t次迭代时天牛质心的坐标；Xt+1为天牛在第t+1次迭代时，天牛质心的坐标；当μ=4，Xt∈[0,1]时，Logistic映射工作处于混沌状态。

将当前最优得到的天牛位置映射到Logistic方程的定义域[0,1]中，生成混沌变量，再将混沌变量逆映射到函数解空间中，对个体进行混沌扰动，通过贪婪规则比较扰动后得到的适应度值与最优天牛位置的适应度值的大小确定是否更新天牛位置。贪婪规则表达式为

(13)

式(13)中：bestX为当前最优天牛位置。

2.1.3 自适应步长因子更新

标准的天牛须搜索算法步长因子与迭代次数呈负相关，迭代次数逐渐增加，天牛的步长则逐渐缩短。一般来说，步长因子的大小会影响算法的搜索能力和寻优效果，当天牛步长因子的取值较大时，算法的全局搜索能力较强，更易跳出局部最优，但是在迭代后期，算法的收敛速度慢，寻优精度低；反之，当天牛步长因子的取值较小时，算法的局部搜索能力越强，能够有更高的寻优精度，但算法易陷入局部最优解。为了平衡算法的全局搜索和局部搜索能力，借鉴文献[20]中的步长更新公式对BAS算法进行改进，提高其步长因子的自适应性，改进的天牛步长因子计算公式为

St+1=Ste-(t/gen)

(14)

式(14)中：gen为总迭代次数；

由式(14)可以看出，天牛移动步长随着迭代次数的增加呈指数型衰减，迭代初期，步长的取值较大，有利于保证算法的全局搜索能力；后期找到全局最优位置后转为局部搜索，此时步长转为较小的值。因此，算法的收敛速度和寻优精度都得到了较大的提升。

2.2 设计适应度函数

在IBAS-BPNN分类模型中，将网络输出层的实际输出值与期望值之间的均方误差(mean square error,MSE )作为适应度值，具体计算公式为

(15)

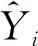
2.3 IBAS算法的时间复杂度分析

算法的时间复杂度是检验算法性能的重要指标，它是指执行当前算法所消耗的时间，也称为算法的渐进时间复杂度。

T(n)=Op[f(n)]

(16)

式(16)中：T(n)为算法执行时间；n为数据规模的大小；f(n)为每行代码执行次数之和；Op为正比例关系。

在BAS中，只有一个天牛个体，且算法只在初始天牛位置和迭代过程了计算了适应度值，当算法维度为k，算法迭代次数为gen时，其时间复杂度为Op(kgen)。在改进的混沌天牛群算法中，天牛种群数为N′，算法迭代和天牛种群寻优为双重循环结构，时间复杂度为Op(N′kgen)。

2.4 IBAS-BPNN分类模型的建立

IBAS-BPNN分类模型通过IBAS算法不断调整神经网络权值和阈值，使适应度值达到最小。适应度值最小时的权值和阈值就是最优的权值和阈值，再将优化后得到的最优权值和阈值应用于BP神经网络中进行训练，最后对测试样本进行分类预测。IBAS-BPNN分类模型的具体算法步骤如下。

步骤1处理数据集，确定网络结构，初始BP神经网络的权值和阈值，将BP神经网络训练得到的均方误差作为适应度值。

步骤2定义种群规模及最大迭代次数，随机生成初始天牛种群。

步骤3计算天牛质心的适应度值，全局最优值bestX及其适应度值f(bestX)。

步骤4根据当前天牛的质心位置确定天牛各触须的坐标，并计算其适应度值。

步骤5根据式(6)得到天牛下一步的预更新位置。在n个反馈个体中与bestX进行比较，比较当前最佳个体的适应度值和f(bestX)的大小。

步骤6如果当前最佳个体的适应度值小于f(bestX)，对当前解进行Logistic混沌优化，产生新解，根据贪婪规则公式，确定是否进行位置更新。否则更新天牛步长。

步骤7判断是否达到当前最大迭代次数，若是，则停止算法迭代，返回IBAS算法的全局最优解bestX，否则跳转至步骤4继续优化。

步骤8BP神经网络将IBAS算法得到的最优天牛个体位置bestX作为新的权值和阈值，对测试集进行预测分析，输出分类结果。

IBAS-BPNN分类模型的构建步骤如图2所示。

图2 IBAS-BPNN分类模型流程图Fig.2 Flow chart of IBAS-BPNN classification model

3 实验

在MATLAB 2018a平台上进行仿真实验，运行环境为Intel RCoreTM i3-8100 CPU，3.60 GHz主频以及16 GB内存，操作系统是Windows 10。仿真实验分为IBAS算法在基准函数上的测试和IBAS-BPNN分类实验两个部分。

3.1 IBAS算法的性能分析

3.1.1 测试函数

在仿真测试中选取3个基准函数F1、F2、F3[21](表1)验证IBAS算法的性能，并将仿真结果与标准的BAS，天牛群搜索算法(beetle swarm antennae search algorithm，BSAS)[22]，天牛群优化算法(beetle swarm optimization algorithm，BSO)[23]，人工蜂群算法(ABC)，PSO进行对比。算法的参数设置为：最大迭代次数为1 000，初始步长S=1，种群数Pop=8，须长d=2，每个函数的搜索维度D=30。

表1 基准函数Table 1 Benchmark function

3.1.2 IBAS的结果与分析

每种算法独立运行30次，将实验结果的最优值Best、平均值Mean和标准差STD作为算法精度和鲁棒性的评价指标，实验结果如表2所示。然后，通过对比结果，比较和分析了算法的性能。为了能更直观地反映算法的性能，各个算法在函数F1～F3上的收敛曲线分别如图3所示。

表2 不同算法的实验结果对比Table 2 Comparison of experimental results of different algorithms

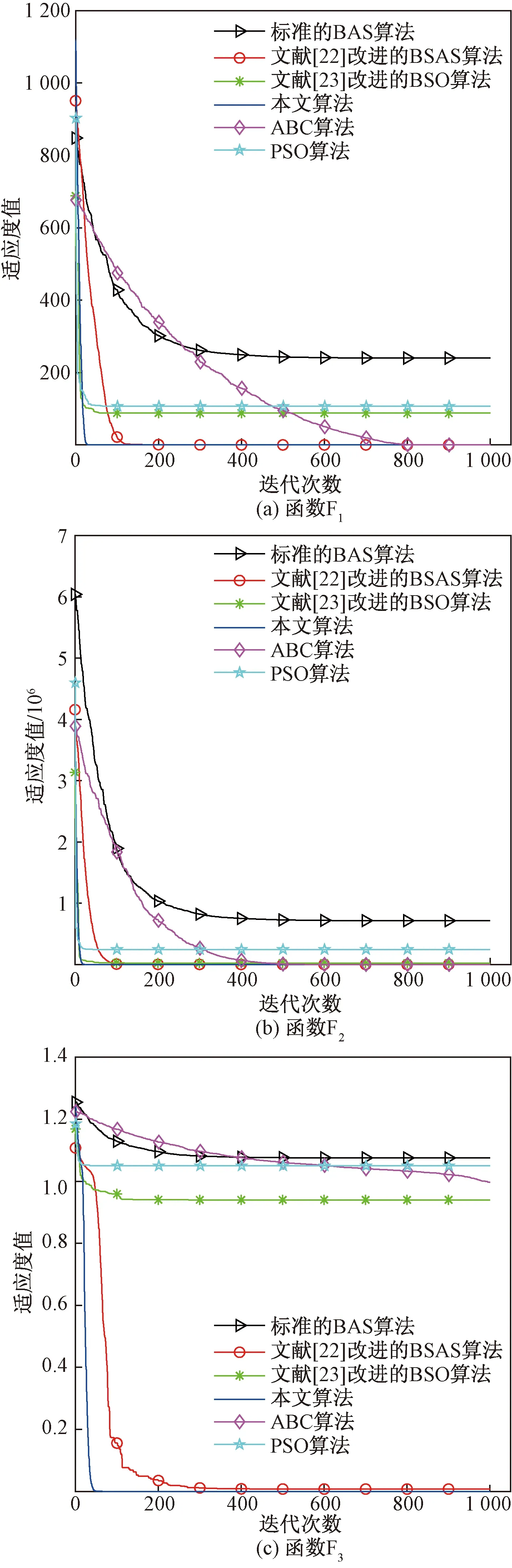
图3 不同算法在函数F1～F3上的适应度值收敛曲线对比Fig.3 Comparison of fitness value convergence curves of different algorithms on function F1～F3

从表2可以看出，IBAS算法在不同的基准函数上都有较好的寻优能力，相较于其他5种算法，其寻优精度得到了很大的提升，且标准差小，表明该算法的实验结果较稳定，鲁棒性好。从图3可以看出，IBAS算法在函数F1～F3上的收敛速度明显比其他5种算法更快，寻优效果更好。因此，IBAS算法达到了预期的效果，具有一定的优越性。

3.2 IBAS-BPNN分类实验结果与分析

3.2.1 数据集

美国加州大学欧文分校(University of California Irvine)提供了专门用于机器学习的UCI数据库。选取UCI数据库中的Iris、Wine、Heart、Mammographic Mass(MM)、Seeds、Wireless Indoor Localization(WIL)6组均衡数据集和Haberman’s Survival(HS)、Breast Cancer Wisconsin(BCW)、Blood Transfusion Service Center(BTSC)、Diabetes、Wilt、Balance Scale(BS)、Car Evalution(CE)7组非均衡数据集作为实验数据。其中，每种数据集随机抽取70%作为训练集，30%作为测试集。这13组数据集的样本数、属性数、类别数、类分布数和隐层神经元数如表3所示。

(1)处理非均衡数据集。HS等7组数据集中各类别的样本数量比存在严重不平衡问题。如果某类样本的数量太少，则此类样本所提供的信息就会非常少，分类模型就会缺乏充足的信息对该类训练样本进行学习和分析，其预测结果的准确率就会降低，从而降低整个分类模型的预测精度。为解决上述问题，采用SMOTE过采样算法处理这7组数据集。

(2)数据标准化处理。由于数据集中各特征属性的量纲不同，如果直接使用原始属性值进行分析，就会导致数值较高的特征属性的作用尤其突出，而数值较低的特征属性的作用就不太明显。为了平衡数据集中各特征属性的权重，去除各属性的单位限制，将其转化为无量纲的纯数值，采用mapminmax函数对输入数据进行归一化处理，将所有数据转化为[0,1]区间的数，mapminmax函数的表达式为

x′i=(xi-xmin)/(xmax-xmin)

(17)

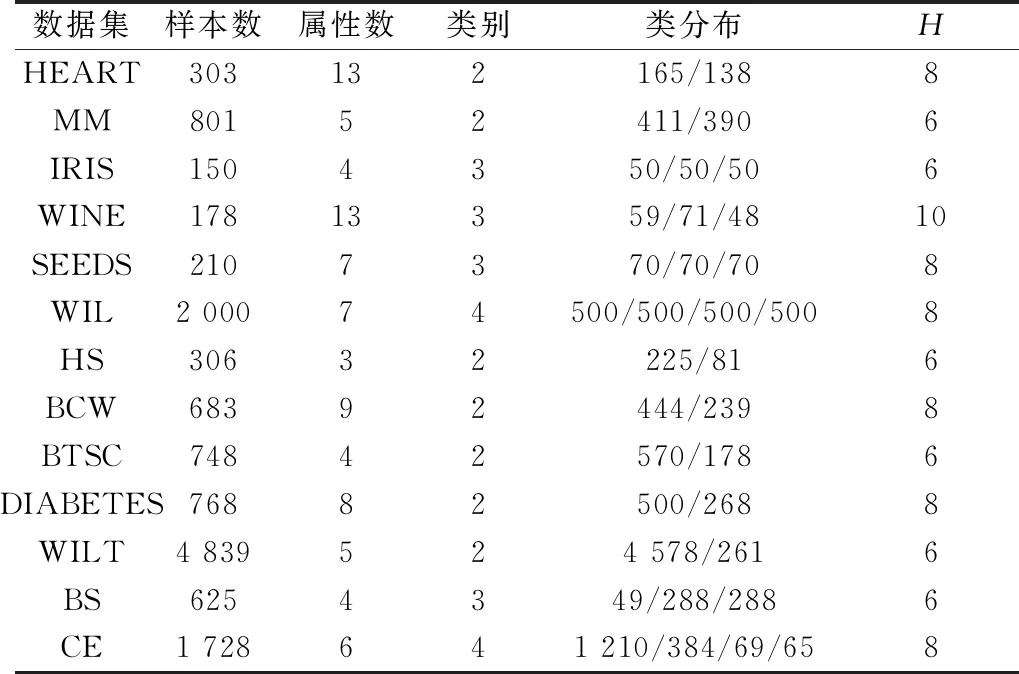
表3 数据集信息Table 3 Dataset information

式(17)中：x′i为归一化的样本数值；xmin为样本数据的最小值；xmax为样本数据的最大值。

3.2.2 评价指标

评价指标是针对分类模型性能优劣的一个定量指标。从分类正确率和Kappa系数两个方面对实验性能进行评价。正确率是最常见的评价指标，通常来说，正确率越高，分类模型越好，正确率Accuracy的计算公式为

(18)

式(18)中：T为全部样本被正确分类的样本数，即实际为i类且被分类模型划分为i类的样本数之和；Nsample为样本总数，每类样本数的总和。

Kappa系数是用在统计学中评估一致性的一种方法，它可以用来作为分类的一项评价指标，其理论上的取值范围是[-1,1]，在实际应用中，一般将其取值范围设定为[0,1]。Kappa系数的值越接近1，表示该分类模型的一致等级越高，其分类越准确。Kappa系数等级分类如表4所示。Kappa系数的计算公式为

(19)

表4 Kappa系数等级划分Table 4 Kappa coefficient classification

式(19)中：Po为总体样本的分类精度，即全部测试样本被正确分类的数量/全部测试样本数量；Pe为SUM(第i类真实样本数×第i类预测出来的样本数)/全部测试样本总数的平方。

3.2.3 实验结果与分析

为验证本文模型的分类效果，选取BPNN、BAS-BPNN、PSO-BPNN、SVM、KNN和决策树ID3分类模型6个分类模型与IBAS-BP分类模型进行对比，其中BPNN、BAS-BPNN、PSO-BPNN都是神经网络分类模型。训练过程中，针对同一数据集，将算法的模型参数设置为相同的值，其中，神经网络迭代次数设置为3 000，学习率设置为0.01，天牛须迭代次数为100，种群数为5，天牛初始步长为1，步长因子为0.95。分别对11组实验数据进行30次实验，以30次实验的分类正确率和Kappa系数作为评价指标，实验结果如表5～表7所示。

表5 基于不同分类模型的均衡数据集的分类正确率Table 5 Classification accuracy of balanced datasets based on different classification models

表6 基于不同分类模型的非均衡数据集的分类正确率Table 6 Classification accuracy of unbalanced datasets based on differentclassification models

表7 基于不同分类模型的Kappa系数Table 7 Kappa coefficients based on different classification models

为了能够更直观地观察和研究7种分类模型在13种UCI数据集上的分类效果，采用簇状图的方式展示各分类模型的分类正确率，如图4所示。

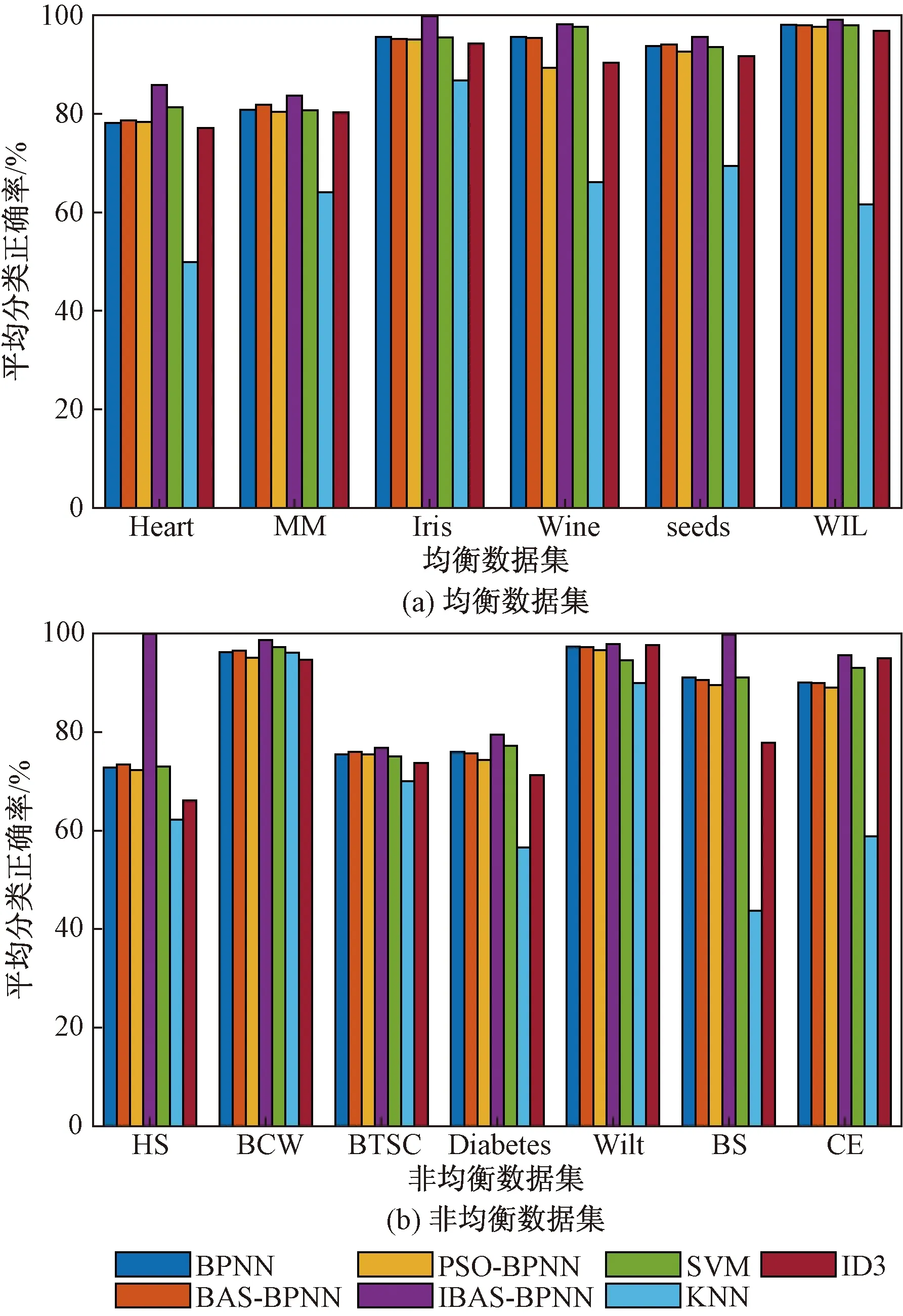
图4 数据集平均正确率Fig.4 Average accuracy of each datasets

如表5、表6所示，从分类正确率来看，IBAS-BPNN在数据集Iris、Wine、seeds、HS、BCW和BS上的最佳分类正确率都达到了100%，在13组数据集上的预测平均值较BPNN提高了7.5%，较BAS-BPNN提高了7.43%，较PSO-BPNN提高了8.45%，较SVM提高了6.94%，较KNN提高了25.62%，较ID3提高了11.03%，有效提高了分类模型的分类精度。从鲁棒性来看，IBAS-BPNN在13组数据集上的平均标准差较BPNN降低了1.25%，较BAS-BPNN降低了1.13%，较PSO-BPNN降低了1.66%，较SVM降低了0.95%，较KNN降低了2.4%，较ID3降低了1.35%，虽然在数据集BTSC中的标准差不是最小的，但整体上IBAS-BPNN的标准差更小，预测结果更稳定，其泛化性更强。

从图4可以看出，所提出的IBAS-BPNN分类模型对13组数据集进行训练后得出的正确率都明显优于其他6种分类模型的分类效果。在均衡数据集中，KNN的分类效果最差，IBAS-BPNN最优；在非均衡数据集中，IBAS-BPNN分类模型进行分类的正确率优于其他6种模型，尤其是经过SMOTE算法处理后的数据集HS。数据集BCW、BTSC和Wilt在分类模型上的分类正确率差距较小。

总的来说，无论是在小规模数据集还是大规模数据集上，无论是在均衡数据集还是非均衡数据集上，IBAS-BPNN模型的分类正确率都是最优的，无论是比较分类正确率的最优值、最差值，还是平均值，IBAS-BPNN的准确率都高于其他6种分类模型。

从表7可以看出，在各数据集中，所提出的IBAS-BPNN分类模型的Kappa系数明显高于其他6种分类模型，表明该分类模型的分类正确率更高。其中，IBAS-BPNN分类模型的Kappa系数在数据集Iris、Wine、seeds、WIL、HS、BCW、BS上Kappa系数超过了0.9，甚至接近1，属于几乎一致的等级。虽然其Kappa系数在数据集Heart、MM、BTSC、Diabetes和Wilt上较低，但也优于其他分类模型。在非均衡数据集HS和BTSC中，其他分类模型的Kappa系数取值在0～0.2，属于分类正确率极低的等级。在13组数据集上的Kappa系数平均值比BPNN提高了0.17%，比BAS-BPNN提高了0.16%，比PSO-BPNN提高了0.19%，比SVM提高了0.22%，比KNN提高了0.55%，比ID3提高了0.19%。SVM分类模型对部分非均衡数据集分类的Kappa系数非常低，尤其在数据集Wilt中的Kappa系数为0，说明SVM对非均衡数据集的分类效果与IBAS-BPNN相比更差。KNN分类模型除了在BCW中的Kappa系数较高外，整体都比较低，说明KNN的分类效果较差，远低于IBAS-BPNN分类模型的分类正确率。

总的来说，IBAS-BPNN在均衡数据集上和通过SMOTE算法处理后的非均衡数据集上的Kappa系数等级好，其分类效果好，正确率高。

4 结论

提出了一种自适应步长因子的混沌天牛群算法用于优化BP神经网络的权值和阈值，建立IBAS-BPNN类模型，减小了天牛须搜索算法陷入局部极值的概率，使得算法的重复性和稳定性得到很大提高，增强了天牛须搜索算法的全局寻优能力。为了验证所提分类模型的有效性，从UCI数据库中选取了6组均衡数据集和7组非均衡数据集进行训练和测试。得出如下结论。

(1)分类结果表明该模型的分类正确率高，分类效果好。

(2)实验证明，该方法能够有效地对分类数据集进行分类，克服了传统BP神经网络的一些固有缺陷。然而，仍需进一步缩短IBAS算法的运行时间和提高其寻优性能，以及提高IBAS-BPNN分类模型在对更多数据集进行分类预测时的分类精度。