计及误差修正的变分模态分解-长短期记忆神经网络短期负荷预测
2022-05-19伍骏杰张倩陈凡李国丽
伍骏杰, 张倩, 陈凡, 李国丽
(1.安徽大学电气工程及自动化学院, 合肥 230601; 2.安徽大学工业节电与电能质量控制协同创新中心, 合肥 230601;3.安徽大学教育部电能质量工程研究中心, 合肥 230601; 4.国网安徽省电力有限公司科学研究院, 合肥 230601;5.安徽大学工业节电与用电安全安徽省重点实验室, 合肥 230601)
随着各省负荷需求升高,电网公司负荷相应地增长,负荷增加的同时伴随着电力负荷波动变大。精确地对负荷的变化趋势进行预测,对电力系统规划和制定发电计划具有不可替代的作用,保障电力系统安全、稳定、可靠地运行[1-2]。
传统的短期负荷预测方法通常分为数学统计法和基于机器学习的方法[3]。经典的数学统计法包括多元线性回归法[4]、自回归移动模型法[5]和指数平滑法[6]等。由于负荷序列的随机性和非线性较强,而基于机器学习的人工智能算法学习能力强,如支持向量机(support vector machine,SVM)[7]、长短期记忆神经网络(long short-term memory,LSTM)[8]和随机森林(random forest,RF)[9]等在处理非线性数据上具有明显优势。然而,采用单一神经网络所得预测结果的精度仍需提高,研究人员在此基础上将多种神经网络进行组合使用,结合不同神经网络各自的特点最大程度发挥其优势。文献[10]采用LSTM和轻梯度提升机的组合预测模型。文献[11]采用XGBoost(extreme gradient boosting)和LSTM的组合预测模型。结果均证明,相对单一算法有更好的预测性能。
随着智能电网的持续发展,仅靠神经网络算法的预测精度已经不满足负荷预测的要求。负荷序列具有随机性和周期性,两者的消长是影响负荷预测精度的重要成因,为最大程度挖掘其中的联系,研究人员倾向于对其先进行频域分解来降低其非平稳性,主要方法包括小波变换(wavelet transform,WT)、变分模态分解(variational mode decomposition,VMD)和经验模态分解(empirical mode decomposition,EMD)等[12-14]。通过先分解后预测的处理,能够有效增强模型的预测性能。文献[15-16]采用VMD算法先分解负荷序列,再使用神经网络模型进行负荷预测,实验结果证明VMD算法能有效降低负荷的非线性,增加模型的预测准确率。前期针对负荷序列分解后的各分量特征,选择不同模型进行预测,将各分量预测结果叠加得到最终结果,实现了负荷预测精度提升[17]。
负荷中始终存在随机因素,因此无法规避模型的预测结果存在误差。通过分析模型的预测值和真实值之间的残差,对残差序列进行建模预测来修正负荷预测值是一种有效手段。在气温、风速、风电和光伏功率等多类预测领域内已证明其有效性[18-20]。文献[21]利用SVR模型对历史光伏功率残差建模,通过预测残差值来修正ARIMA的预测值。文献[22]在使用随机森林算法对电力负荷预测后,利用粗糙集理论克服预测结果峰值附近的误差,有效减少预测值的误差。
基于此,以安徽省某地区负荷为研究对象,基于“分解-预测-误差修正”的思想构建短期负荷预测模型,以不同预测模型作为对比,为研究精确的短期负荷预测提供科学依据。
1 算法理论
1.1 VMD算法定理
VMD信号处理算法由Dragomireskiy等[23]于2014年首次提出。该算法可类比为维纳滤波器组,具有自适应分解功能,可将非平稳的信号分解为多个具有中心频率的有限带宽的模态分量,有效降低了信号的非平稳性。
VMD的具体步骤即构造和求解变分问题。首先将负荷序列分解为多个模态分量,确保模态分量为具有中心频率的有限带宽分量,并且估计带宽之和最小,所有模态分量之和等于初始信号,可表示为
(1)
式(1)中:{uk}={u1,u2,…,uK}为k个模态分量的集合;{ωk}={ω1,ω2,…,ωK}为各个模态对应的中心频率;∂t为解析信号的梯度;δ(t)为狄拉克函数;t为采样时刻;f(t)为初始信号;e-jωkt为中心频率ωk所对应指数项。
根据式(1),同时使用二次惩罚项α和拉格朗日乘子λ,将约束问题非约束化,更新的拉格朗日函数表达式为
L({uk},{ωk},λ)=
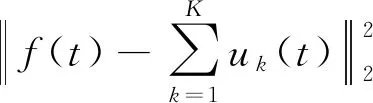
(2)
式(2)采用乘数交替方向法进行求解,更新后的uk和ωk相应的表达式分别为
(3)
(4)
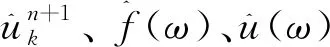
1.2 长短期记忆神经网络
LSTM属于循环神经网络(recurrent neural network,RNN)的一种变体。相较传统RNN的长期依赖问题,LSTM在RNN基础上在每个细胞状态中加入门来控制信息是否保留,改进了RNN无法长序列的问题。目前,LSTM在长序列的处理中得到普及。
LSTM的每个细胞共有遗忘门、输入门和输出门三部分,分别决定信息的过滤、保存和生成,完整结构如图1所示。
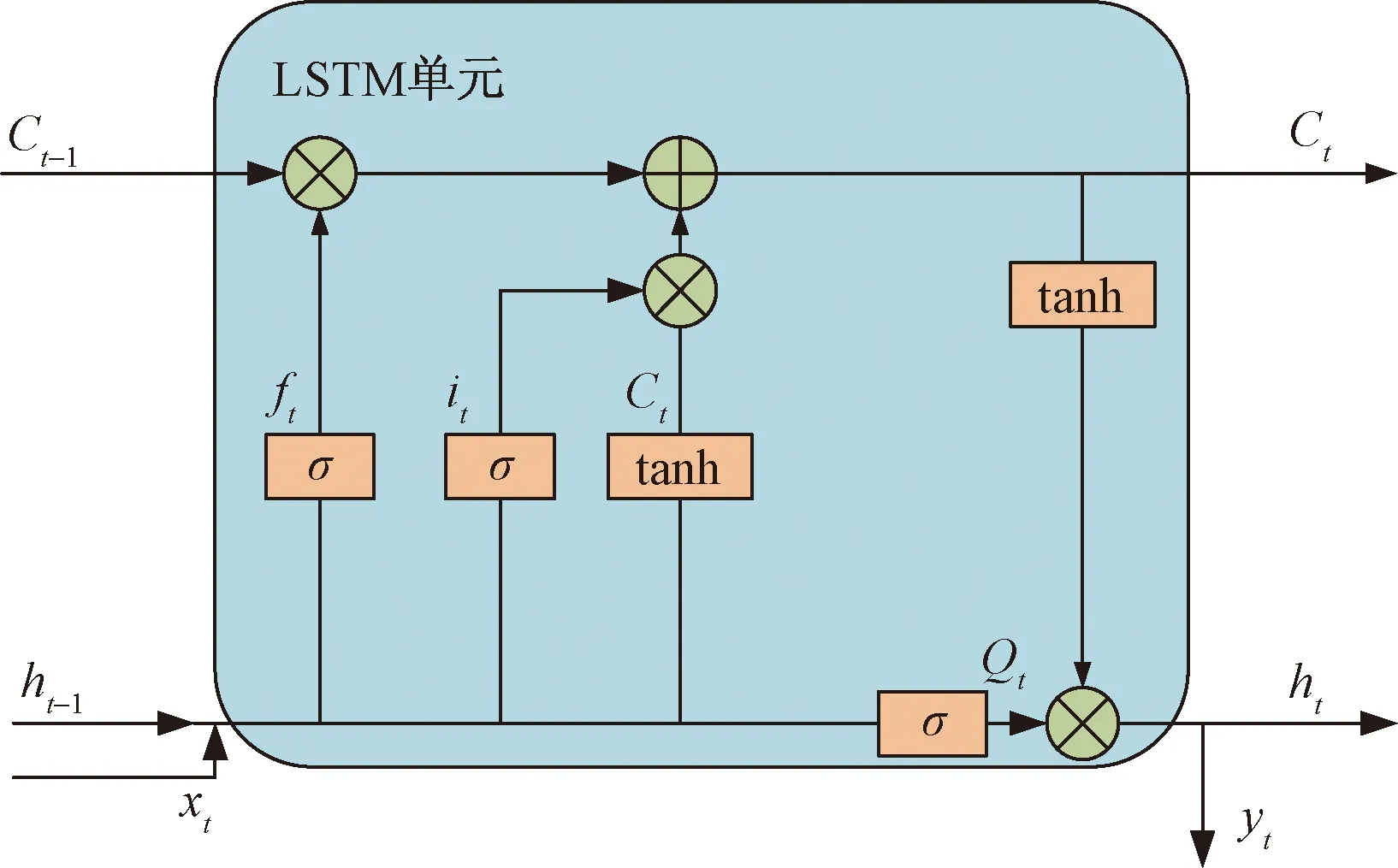
Qt为LSTM结构单元的输出门;yt为当前节点输出图1 LSTM结构单元Fig.1 Structure unit of LSTM
LSTM的工作步骤如下。
步骤1通过遗忘门确定分解后的各本征模态函数(intrinsic mode function,IMF)中需要滤除的信息部分。将当前输入xt和上一时刻输入ht-1通过sigmoid函数σ确定是否过滤。
ft=σ[Wf(ht-1,xt)+bf]
(5)
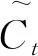
it=σ[Wi(ht-1,xt)+bi]
(6)
(7)
(8)
步骤3首先由sigmoid函数确定单元输出部分,再将单元状态 通过tanh和sigmoid门输出部分相乘得到模型的预测值点。
(9)
ht=ottanhCt
(10)
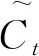
1.3 支持向量回归
SVR是一种求解回归问题的高效机器学习算法,其本质为寻找最优超平面进行建模。对给定的预测误差集(xn,yn),使其所有样本点与回归曲线的“总偏差”最小。其中,xn为输入负荷误差值,yn为预测负荷误差值。因此,SVR问题转化为
(11)
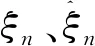
对应约束条件为
式(12)中:ε为回归偏差。
到底为什么会有屋面曲线的设计?因为历史上没有文字记载,大家都在议论与猜测,如果你有更科学的解释,请记得告诉我呀!
2 组合预测模型
2.1 基于VMD-LSTM和SVR的短期负荷预测模型
所设计预测方法的流程图如图2所示。预测方法按照“分解-预测-修正”的思路,具体步骤如下。
步骤1选用VMD算法分解负荷历史序列,获得多条较平稳的子序列。
步骤2将各分量数据进行归一化。归一化后的数据输入LSTM经过训练和测试,得到各分量的预测分量。
步骤3合并各预测分量,重构为初始负荷预测值。
步骤4由实际值和初始负荷预测值得到残差值,输入SVR得到预测残差值。
步骤5将预测残差值补偿至初始负荷预测值以进一步修正预测结果,获得所需负荷预测值。
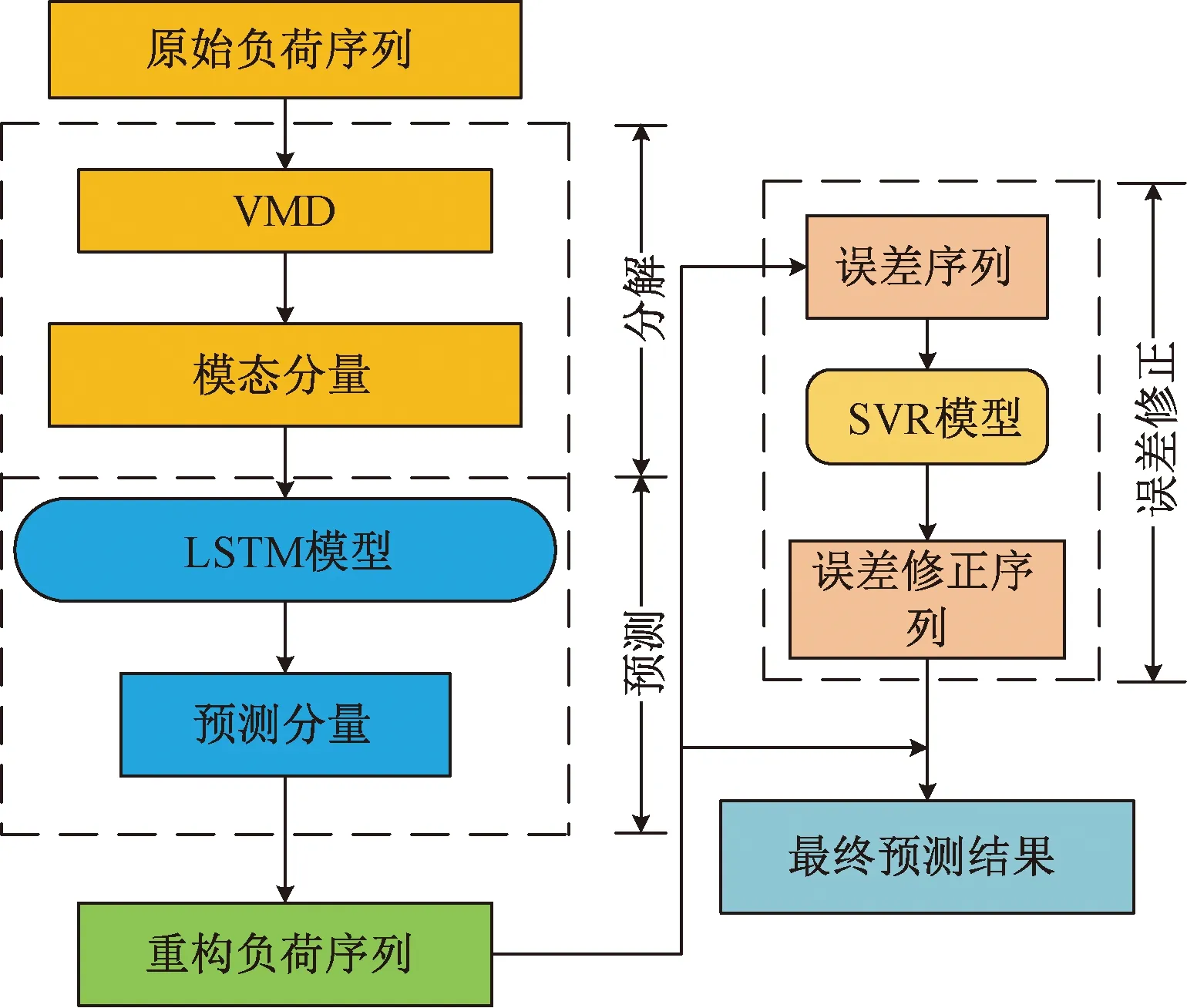
图2 VMD-LSTM-SVR流程图Fig.2 Flowchart of VMD-LSTM-SVR
2.2 模型性能评价指标
通过数据能够直观反映模型的性能。采用平均绝对百分比误差(mean absolute percentage error,MAPE),平均绝对误差(mean absolute error,MAE),均方根误差(root mean squared error,RMSE)和模型拟合系数R2来评价。其中,MAE值,MAPE值越小和RMSE值越小,表示模型越完美,得到的预测值更趋近真实值;R2值越趋近1表示预测结果的拟合度越趋近真实值。其计算公式为
(13)
(14)
(15)
(16)
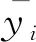
3 算例分析
3.1 负荷数据集
实验选用安徽省某地区2020年3月1日—2020年3月8日的负荷样本,采样时间间隔为15 min,共计768个采样点,前6 d为训练集,后2 d为测试集。初始负荷数据集如图3所示,可以看出每日负荷具有类似的变化趋势,呈现一定的规律。
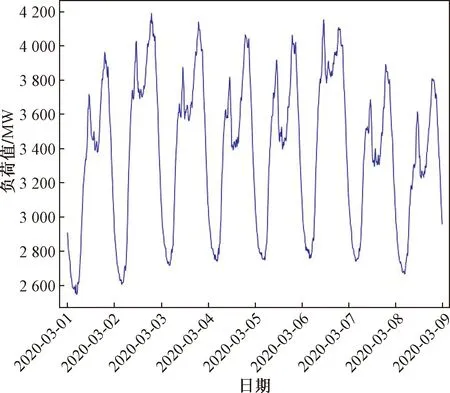
图3 原始负荷序列Fig.3 Original load sequence
3.2 基于VMD-LSTM组合预测
选择VMD算法对初始负荷分解,将其转化为非平稳性的子序列,提高LSTM模型的预测准确率。VMD的模态分量个数K设置为5,初始中心频率ω′=0,收敛准则容忍度γ=10-6,惩罚因子α=2 000。负荷序列分解结果如图4所示。
根据上文的流程,对分解后的序列进行预测,分量预测结果之和即为初始预测值。在预测前,对分解后的负荷分量进行归一化处理,加快神经网络模型梯度下降法求解最优解的速度和防止训练发散,归一化方法可表示为
(17)
式(17)中:y*为归一化后的值;yi为负荷的实际值;ymax和ymin分别为最大和最小负荷值点。
归一化后的数据划分为训练集和测试集来构建LSTM负荷预测模型。LSTM的隐藏层数目影响模型的预测精度。隐藏层数多时,预测效果越好;层数少时,训练时间相应较短。经过实验证明,设置隐层数目为3层时,可保证训练用时少的同时有较好的准确率。网络训练算法选择ADMA算法,训练轮数为150次,初始学习率设置为0.005,经过100次训练后学习率通过乘以衰减因子0.2来降低。输出层使用全连接层,输出值反归一化得到预测结果,如图5所示。

图4 经过VMD分解后各分量Fig.4 Components after VMD decomposition
由图5可以看出,经过该模型预测后的结果有较好的拟合效果,而在清晨时段负荷持续上升和夜晚时段负荷持续下降阶段处存在一定误差,结果如表1所示。如图6所示,VMD-LSTM所得预测结果与实际值的误差序列含有较强的非线性。因此,考虑使用SVR模型预测误差值来补偿初始预测值。其中,SVR的核函数选择能较好处理非线性序列的径向基函数(radial basis function,RBF),惩罚参数C取100。
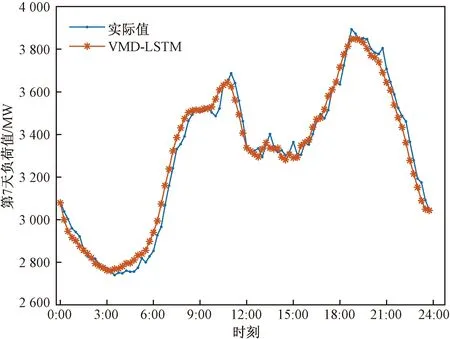
图5 VMD-LSTM预测结果Fig.5 Prediction results of VMD-LSTM

表1 负荷上升和下降处预测误差Table 1 Prediction error at load rise and fall
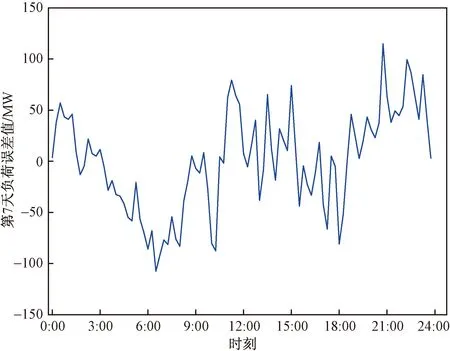
图6 VMD-LSTM的误差值Fig.6 Error value of VMD-LSTM
3.3 基于SVR的误差修正
误差修正通常需要建立从属预测器来预测误差序列。将预测后的残差序列与初始预测结果叠加,获得修正后的预测结果。修正前后的负荷误差绝对值针状图如图7所示,可以看出,经过修正后,有约90%的负荷点的误差绝对值减小,这表明SVR的误差修正模型能够提升整体负荷预测精度。
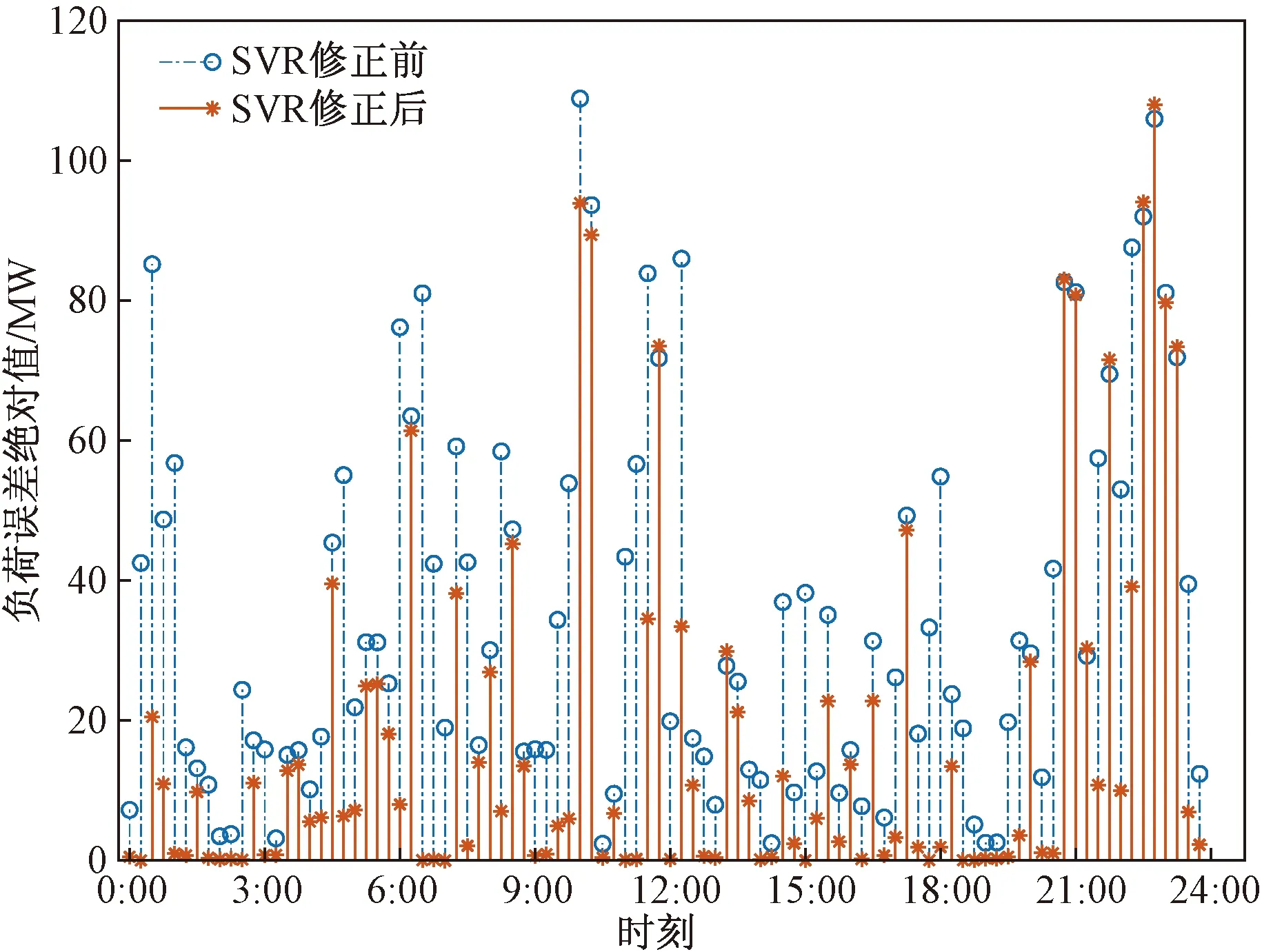
图7 修正前后误差绝对值Fig.7 Error value before and after correction
3.4 结果分析
为检验所提模型的实际效果,对相同的负荷数据分别采用反向传播(back propagation,BP)神经网络模型、LSTM神经网络模型、VMD-LSTM模型进行对比。预测结果对比和预测评价指标分别如图8、表2所示。
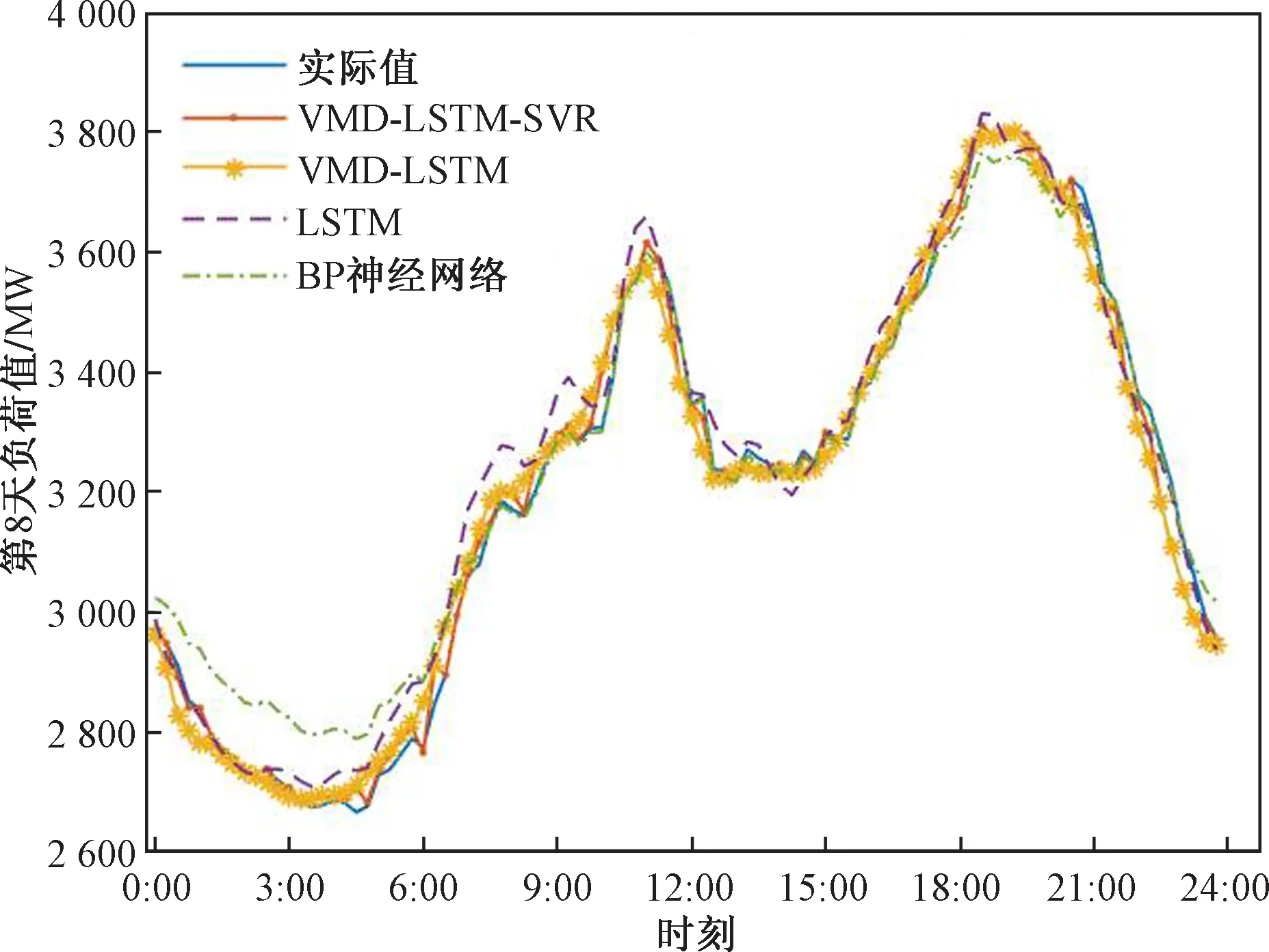
图8 不同模型预测效果比较Fig.8 Comparison of prediction effects of different models
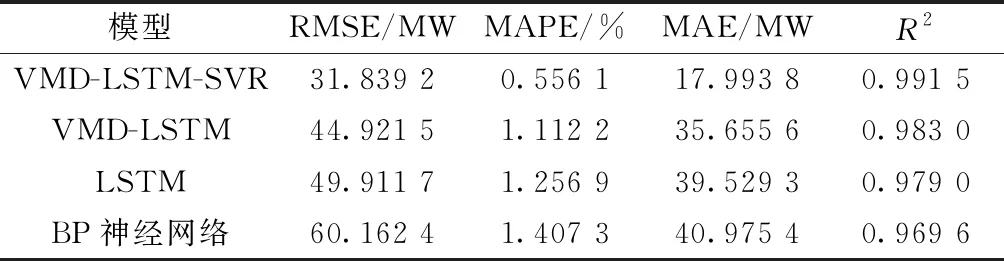
表2 不同模型的预测评价指标Table 2 Predictive evaluation indicators of different models
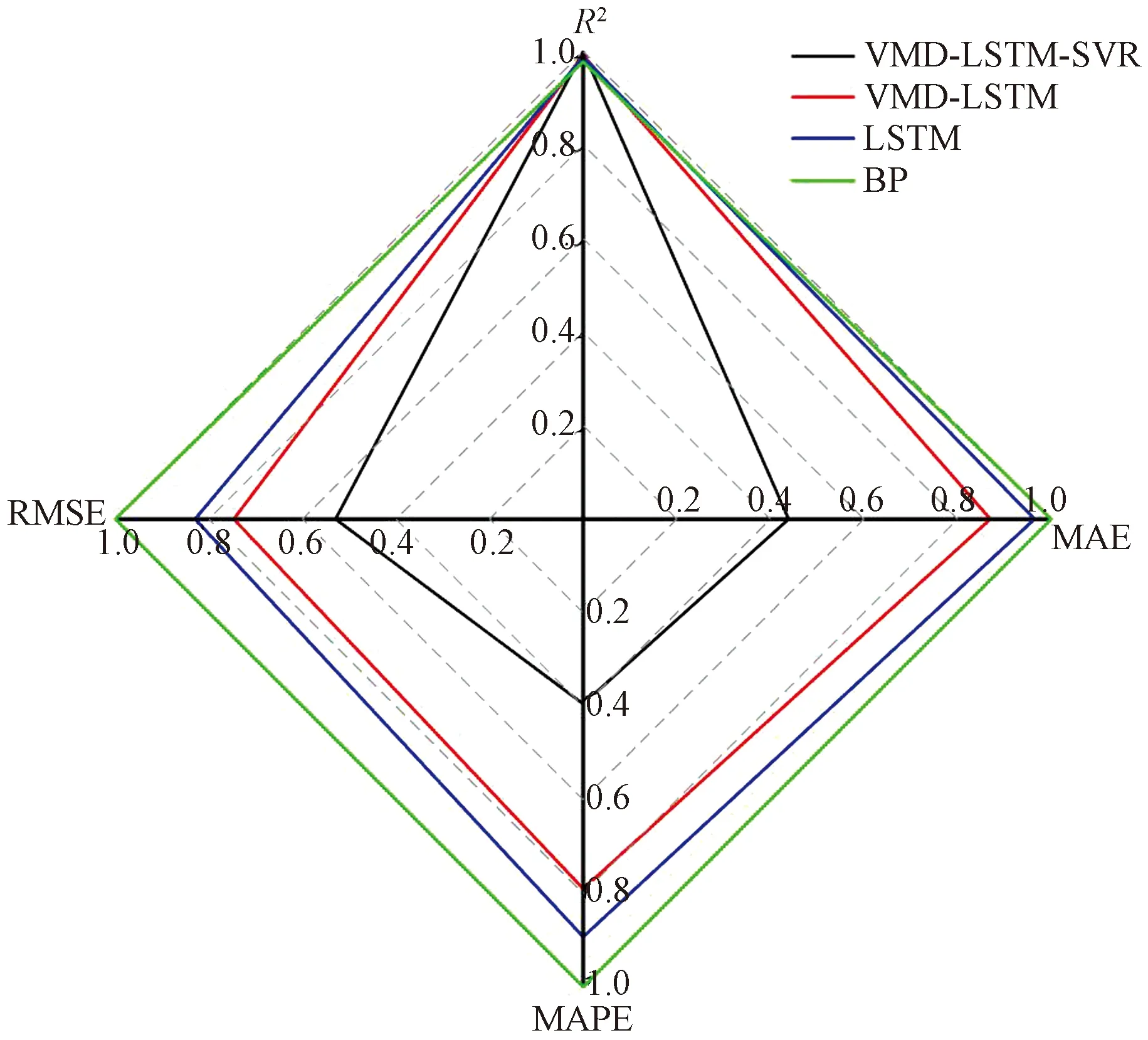
图9 不同模型误差指标比较Fig.9 Comparison of error indicators for different models
结合表2和图9看出,BP神经网络因其存在局部极小化问题,且网格结构选择不一,预测结果对比LSTM神经网络具有明显的不足;同时,将序列进行分解-预测-重构操作后,预测结果的准确率有显著提升,VMD-LSTM对比单一LSTM,RMSE值,MAPE值和MAE值分别降低了10%,11.51%和9.80%,数据拟合程度R2提高至98.30%,证明了变分模态分解能够有效降低负荷序列的不稳定性,从历史数据中提取信息,使LSTM模型有更好的负荷预测能力;本文方法在此基础上加入误差修正,数据显示该方法能够进一步增加预测准确率。其中,RMSE值,MAPE值和MAE值分别降低了29.1%、50%和49.5%,数据拟合程度R2提高至99.15%,证明了所设计模型在短期负荷预测中具有有效性。
4 结论
(1)VMD方法可以提取出隐藏在负荷序列中的周期性和规律性,有效提高下一步神经网络的预测准确性。基于SVR的误差修正部分可以进一步提高VMD-LSTM模型的预测准确性。
(2)通过安徽省某地区负荷作为实际案例进行计算,实验结果证明,本文模型有效提高了预测效果。后续工作可着重于负荷分解后分量的特征进行研究,针对分量的特点选择更适宜的深度学习模型,最大程度发挥频域分解的作用。
