基于权值时变模型的矿井突水最优逃生路径的动态选择
2022-05-19于丹颜伟李劭昱
于丹, 颜伟,2*, 李劭昱
(1.山东科技大学能源与矿业工程学院, 青岛 266590; 2.山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地, 青岛 266590)
在煤矿建设和采矿生产中,矿井突水是仅次于瓦斯爆炸的主要突发性灾害之一。尽管矿井突水监测及预警技术研究及应用已进行多年,但随着煤矿开采深度的逐步增加,采煤环境的水文地质条件将更加复杂多变,矿井突水事故仍时有发生[1]。矿井突水一般来势凶猛,不仅会在短时间内淹没煤矿巷道和生产设备,破坏生态环境,还会造成人员重大伤亡。因此,为了让井下矿工在发生突水之后,快速、准确地选择出最优的逃生路径(即从逃生地到安全地所用时间最短、危险性最低的安全撤离路线)[2]是应对矿井突水事故的关键。
当前,关于矿井突水逃生路径选择方面的相关研究主要分为两个方面:一是在研究影响井下矿工逃生因素方面。除考虑突水灾害水位高度对逃生影响外,还应考虑巷道类型、风速风向、坡度、局部障碍物数量[3]以及是否有交通工具[4]等因素,这些影响因素使得巷道节点之间的距离不再是绝对距离而需要用当量长度来表示;二是在逃生路径选择模型构建及算法方面。主要是对传统算法的改进以及朝着建立更符合现实情况的动态逃生路径选择模型这两个方向进行研究。蔡明杰等[5-6]通过对交叉、变异算子进行重构,在适应度函数中加入安全通过概率来改进传统的遗传算法;通过对松弛点入队位置调整来优化SPFA(shortest path faster algorithm)算法,从而提高算法搜索突水救援路线的效率。刘梦杰等[7]提出了一种新型路径搜索算法——双向A*算法,根据评估函数来确定搜索方向,使得选择的逃生路径节点更少,大大提高了算法的搜索效率。Yan等[8]对蚁群算法进行了改进:一是利用巷道分区特性影响蚂蚁的行为,提高蚂蚁的搜索效率;二是修改了蚁群会合策略和蚁群死亡规则,以提高蚁群算法的性能。王鹏等[9]将改进萤火虫算法应用到突水环境的路径规划中,并与A*算法进行比较,结果表明:改进后的萤火虫算法选择的路径更优,具有大范围搜索优化能力。周越等[10]为研究实时水位高度变化对逃生路径选择影响,提出时间当量长度模型,并通过改进Dijkstra算法进行求解。Zhao等[11]建立了三维矿井巷道网络,结合实时变化的水位及巷道的可通行性,运用Dijkstra算法实现了基于3D网络模型的最佳逃生路径搜索。Du等[12]、Wu等[13]考虑实时水位高度变化对逃生时间的影响,通过改进Dijkstra算法,提出了并行时变最早到达算法;实现人员逃生智能动态路径搜索,生成安全迅速的井下人员最优逃生路径。
综上可知,虽然学者们研究了基于实时灾害影响的逃生路径选择模型及算法,但在考虑突水灾害因素方面只考虑水位高度,而实际情况是不同时刻巷道内的水流速同样对逃生路径选择影响很大。为此,提出一种同时考虑水位高度和水流速的矿井突水最优路径选择模型,将所研究的时间进行分段,分别估算各时间段内各巷道的水位高度和水流速,用于判断不同时段内各巷道的危险性,再将其加权到巷道初始当量长度中形成权值时变模型,并通过改进的Dijkstra算法来对权值时变模型进行求解,从而动态选择出安全可靠的最优逃生路径。
1 最优逃生路径选择原则分析
根据实际矿井突水应急避灾的情况,结合煤矿安全管理,提出矿井突水灾害逃生路径选择的两大原则:安全性原则、时间最短原则。
1.1 安全性原则
由于矿井突水发生后,大量的地下水会迅速涌入巷道。水流作为最主要的灾害因素,其高度及流速严重影响工作人员的逃生效率,因此,为了井下矿工的人身安全和提高逃生效率,在选择路径时,尽量避开有水灾的路径或者选择水位较低的路径。
1.2 时间最短原则
在矿井突水发生的情况下,受灾矿工生还的可能性与逃生时间成反比,逃生时间越长,生还的可能性越低。因此,需要找出花费时间最短的路径,而最短距离提供的路径,其用时不一定最少,所以在研究这方面内容时,逃生的时效性一般以巷道的“当量长度”衡量,即找到距离安全出口当量长度最短的路径[14]。
2 最优逃生路径模型构建
2.1 模型整体设计
矿井突水发生后,由于受到水流因素的影响,井下矿工在逃生时不能随意选择逃生路径,而应该结合巷道内的环境来选择。依据水流漫延的方向,将巷道网络图由无向图变成有向图,有利于确定正确的疏散方向,进而排除无效疏散巷道;一些巷道被水淹没或者危险系数过高而不能通行的巷道,也应该在搜索路径之前排除;在计算出巷道的危险系数的基础上,再考虑巷道固有环境对矿工通行的影响。据此,本文综合考虑了突水水流和巷道固有环境两类因素,为井下矿工设计了一种矿井突水最优逃生路径模型,如图1所示。
2.2 突水漫延方向
发生突水时,水流会在水力梯度的作用下迅速向周围连通的巷道漫延,若突水点高于相邻巷道高程时,会发生下向漫延;当突水点以下的巷道充满水之后,水流就会沿着突水点之上的位置开始上向升涨。根据水流漫延的方向,将巷道网络图由无向图变成有向图,有利于确定正确的逃生方向。由于在水流下向漫延过程中,水流受到重力作用影响自动找到最低的巷道位置,所以从巷道突水点到这样一段的巷道不应该作为选择的逃生路径。

图1 矿井突水最优逃生路径模型Fig.1 Optimal escape path model of mine water inrush
2.3 危险系数的计算
水流是影响逃生路径选择的最重要的动态因素,这里将水位高度和水的流速对人体稳定性的影响作为求解危险系数的影响因子。
2.3.1 计算巷道内水位高度
当已知突水流量和时间时,利用插值计算得出对应时间段内的水位高度(不考虑围岩渗入量和设施排水量),计算公式为[15]
(1)
(2)
式中:lx为流入巷道的水流长度,m;Q为突水流量(恒定),m3/s;t为突水时间,s;S为巷道横截面积,m2;hx为水位高度,m;h0为起点节点标高,m;h1为终点节点标高,m;l为涌入水流的巷道总长度,m。
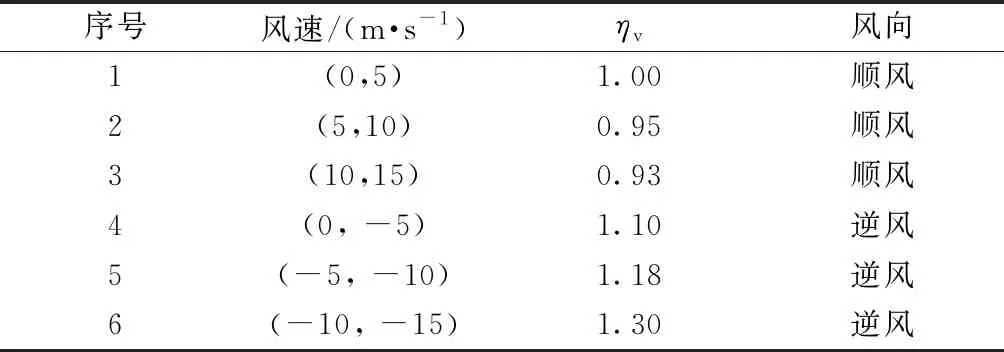
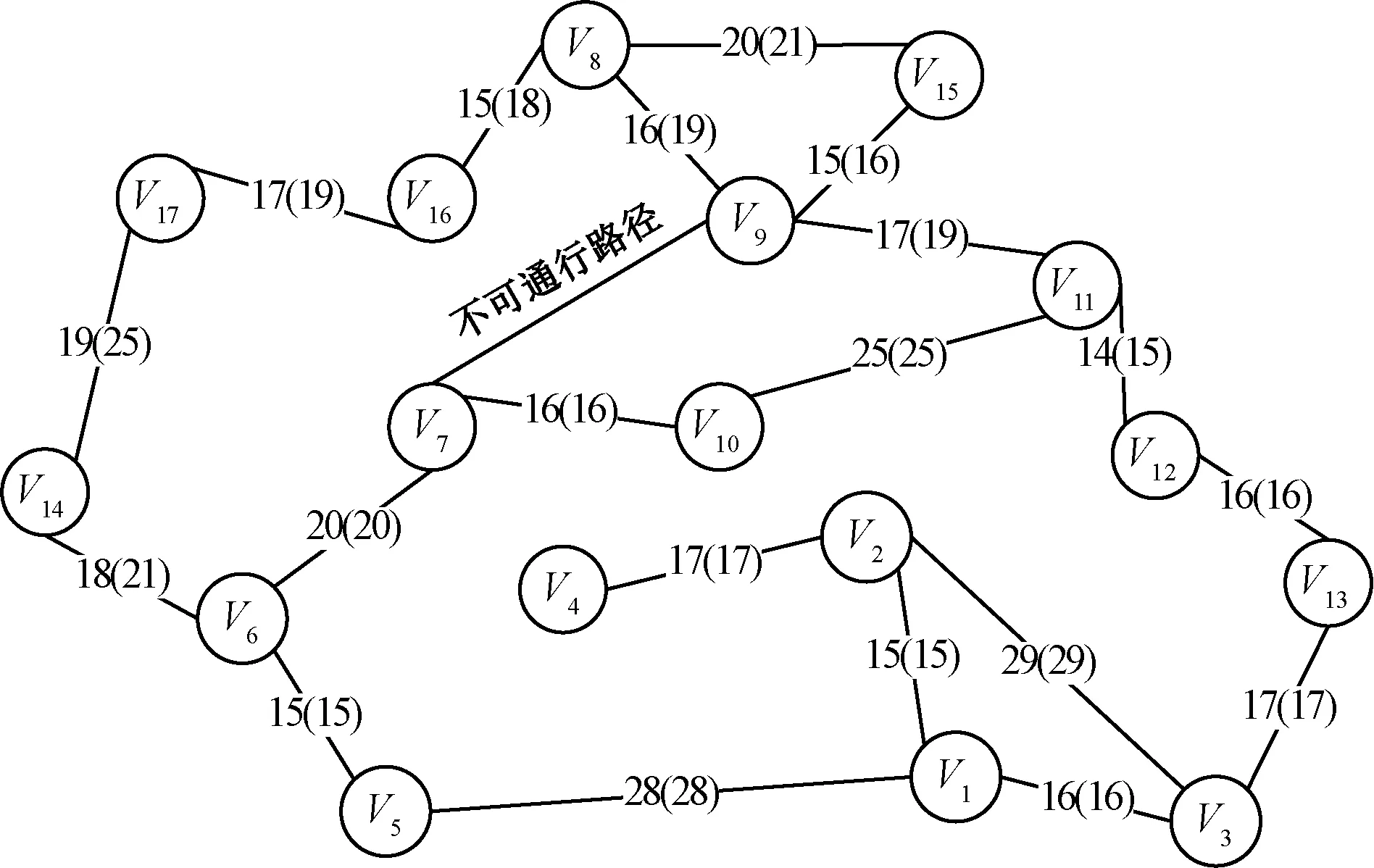
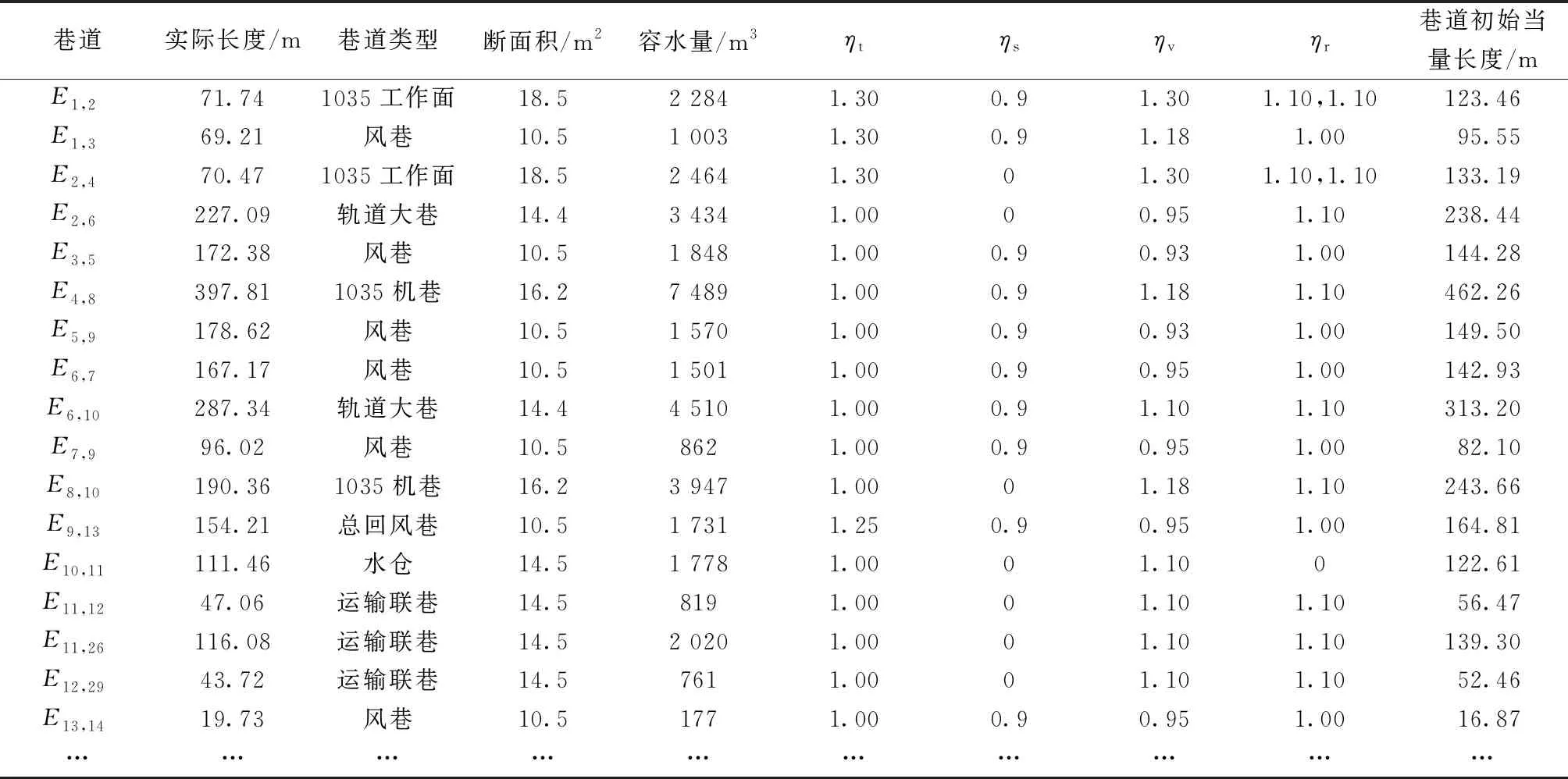
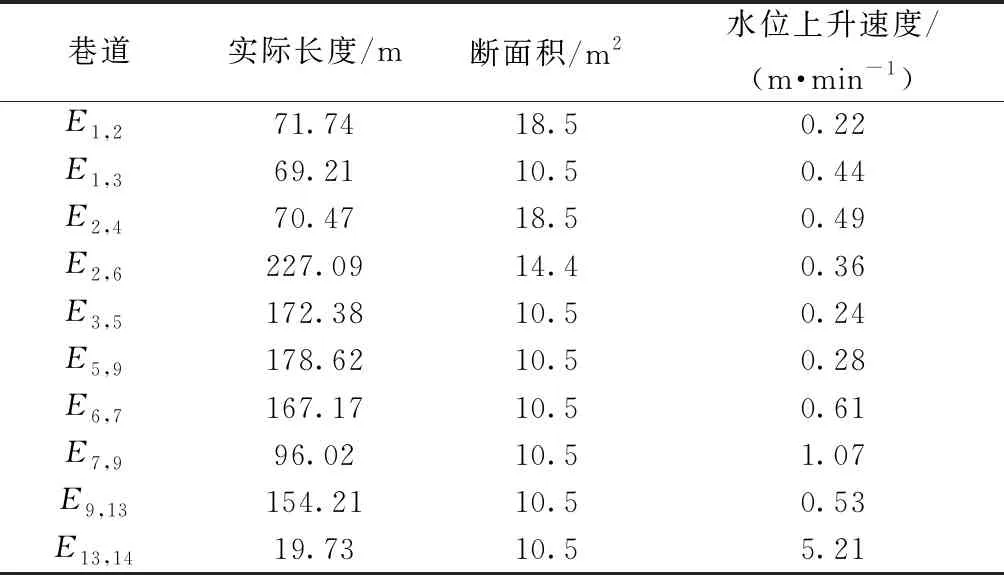
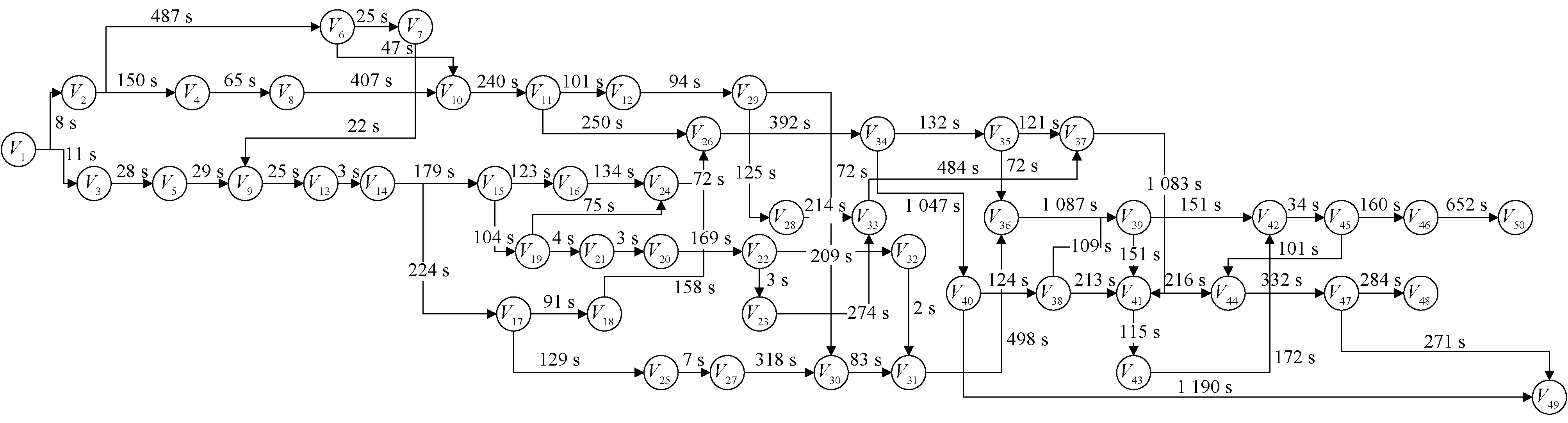
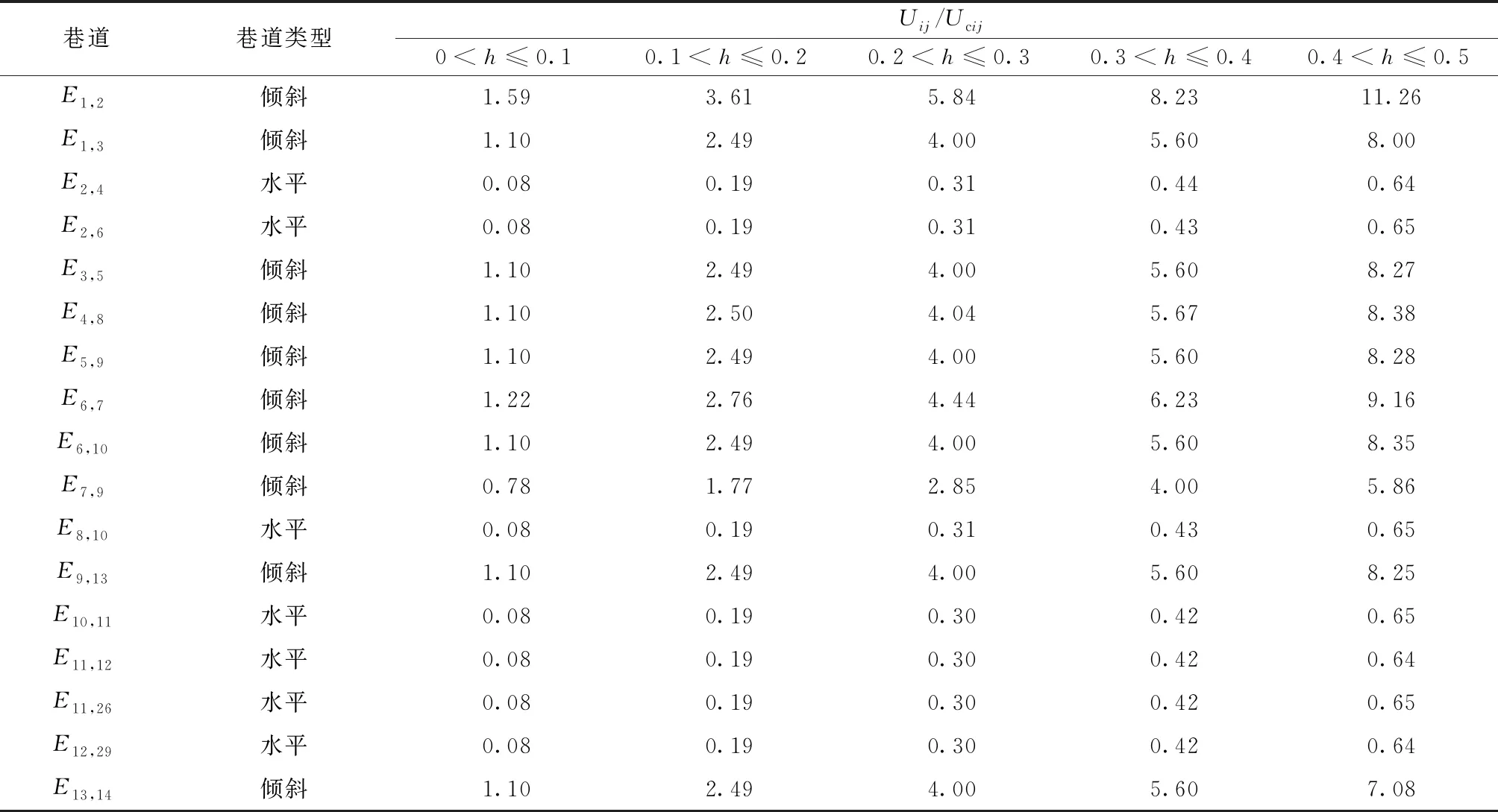
基于上述所求的水位高度,来估算每段时间不同巷道内的水位上涨速度,假设当前时刻为0,t为突水时间(以秒为单位),将突水时间进行时段划分为T0 2.3.2 计算巷道内水流速 由于风速和障碍物对巷道内水流速的影响比较抽象,难以用数学方法进行定量计算,因此只考虑巷道的种类对水流速的影响。在不同类型的巷道中,由于巷道断面、井巷坡度、巷道壁粗糙度等因素有所差异,水的流速是不同的且随着时间变化。 根据文献[16]分别求出水平、竖直、倾斜这3种巷道类型中的水流速,具体计算公式如下。 (1)水平巷道水流速。 (3) 式(3)中:g为重力加速度;λ为沿程阻力系数;hf为沿程水头损失;R为水力半径,R=A/χ,其中,A为过水断面面积,χ为湿周,χ=b+2h,b为巷道底部宽度,h为水位高度;C为谢才系数,C=R1/6/n,其中n为粗糙系数,n取0.02;J为水力坡度。 (2)竖直巷道水流速。 (4) 式(4)中:m为水流单位质量;hvertical为竖井高度。 (3)倾斜巷道水流速。若斜井倾斜角度小于45°时,由水平巷道水流速度计算公式结合倾斜角度求得;若斜井倾斜角度大于等于45°时,由竖直巷道水流速度计算公式结合倾斜角度求得。 2.3.3 巷道危险性判断 首先根据Xia等[17]通过研究洪水的水位高度及水流速对人体发生跌倒失稳的影响得到临界流速Uc计算公式为 (5) 式(5)中:d为水位高度;ρf为水的密度,取1.0×103kg/m3;hp、mp分别为人的身高及体重(取矿工们的平均身高和平均体重分别为1.70 m、70 kg);由中国成年人身体结构特征率定出经验参数a1=0.633、b1=0.367、a2=1.015×10-3m3/kg、b2=-4.927×10-3m3;参数α和β与人体形状有关,对于其率定,使用Karvonen等[18]提出的真实人体跌倒失稳的试验方法得到α=7.867 m0.5/s,β=0.462。 然后根据巷道内水的平均流速与临界流速的比值可以计算人体在每条巷道的危险系数Sij,计算公式为 Sij=Uij/Ucij (6) 式(6)中:Uij为某时间段巷道Eij内的水的平均流速,m/s。Ucij为某时间段人体发生跌倒失稳时的巷道Eij内临界流速,m/s;Sij为人在有水流的巷道Eij中逃生的危险系数。 最后根据Sij值将人体在巷道中通行的危险程度划分为4个等级(参考文献[19]中洪水对人的危险等级进行划分)如表1所示。 表1 危险等级Table 1 Risk grade 井下环境具有特殊性,含有多种阻碍矿工通行的因素,如巷道类型、风速风向、坡度、障碍物、照明情况、是否有交通工具等都会对逃生产生影响,相关影响因素可以转化为巷道初始当量长度来表示。 2.4.1 巷道影响因子的确定 结合矿井的巷道环境以及现场模拟分析,选取巷道类型、巷道坡度、风速风向、局部障碍物的数量,作为影响井下矿工逃生的主要静态影响因素。将巷道类型、巷道坡度、风速风向、局部障碍物的数量对巷道初始当量长度的影响系数分别记为ηt、ηs、ηv、ηr。影响系数的计算公式为[20] (7) 式(7)中:η(Eij)为某因素对巷道Eij初始当量长度的影响系数;T(Eij)为受到某因素影响时通过巷道Eij的通行时间;t(Eij)为不受某因素影响时通过巷道Eij的通行时间。 根据式(7)所求得各因素对巷道初始当量长度的影响系数的计算结果如表2~表5所示。 表2 巷道类型对巷道初始当量长度的影响系数ηtTable 2 Influence coefficient ηt of roadway type on initial equivalent length of roadway 表4 风速风向对巷道初始当量长度的影响系数ηvTable 4 Influence coefficient ηv of wind speed and direction on initial equivalent length of roadway 表5 局部障碍物对巷道初始当量长度的影响系数ηrTable 5 Influence coefficient ηr of local obstacles on initial equivalent length of roadway 2.4.2 巷道初始当量长度的确定 假设节点Vi和Vj间巷道Eij的实际长度为l(Eij),将巷道的各静态因素影响系数加权到其对应的实际长度中,得到该条巷道初始当量长度值L(Eij)为 (8) 式(8)中:n为巷道Eij上障碍物数量;ηrm为第m个局部通行障碍物影响巷道正常通行的系数。 作为应急逃生方案的决策者,在对逃生路径进行选择时,一般按照当量长度最小的路径前进,所用时间最短,成功逃生的概率就越大。所以当煤矿发生突水事故时,矿工选择的最优逃生路径就是从井下突水点到安全出口的所有的安全、可能路径中,找出当量长度最小的逃生路径。假设逃生人员从受灾点到安全出口的所有路径集合为P,P中当量长度最小的路径即所求的最优逃生路径由n条巷道组成,Sij为巷道内不同时段下的通行危险系数,建立矿井突水灾害逃生路径选择的目标优化数学模型,可表示为 (9) 约束条件: (10) (11) (12) xij={0,1},i=1,2,…n;j=1,2,…,n (13) 式中:fL(P)为路径P的当量长度;Lij为巷道(Vi,Vj)的初始当量长度,Lij=0,∞分别为Vi=Vj、Vi与Vj不相邻,Lij>0即为式(8)所求得的值;式(11)表示xij的取值构成从源节点V1到目的节点Vn的一条可行逃生路径;式(12)表示逃生路径中不含回路;xij为决策变量,xij=0,1分别表示巷道(Vi,Vj)不在、在选定的路线P上。 由于水位高度和水的流速随着时间变化,那么在特定时段内用静态路径选择算法所求的最优路径,无法证明在全时域保持最优;为了动态描述各巷道在不同时间下的危险性情况,根据文献[21],将所研究的时间分为K个时段,基于上述数学模型求解出每个时段内各巷道的危险系数,加权到巷道初始当量长度上以此作为逃生路径的危险性权重,而巷道权值随不同时段的危险性权重大小变化而变化。传统的Dijkstra算法不能解决最优路径的动态选择问题,所以对该算法进行改进,步骤如下。 节点与节点之间的连线上的数值为巷道权值,如V16与V17之间的17(19),其中17为当前时段下的巷道权值,括号里的19为更新后的巷道权值图2 巷道网络示意图Fig.2 Roadway network diagram 步骤1初始化。确定突水点为Vi,安全节点为Vj,将突水点Vi到节点Vx的最小累计权值记为Wix,Pix为到节点Vx所经过的路径节点集合。利用集合Q表示最小累计权值已知的节点,用集合U表示最小累计权值未知的点。初始时,Q只包含突水点Vi,U中包含除点Vi外的其他节点;突水点Vi相邻节点的权值Wi和路径Pi可以从巷道网络图中得到,不相邻的节点的权值为∞。在图2中,设突水点为V8,安全节点为V4,巷道网络权值时变周期为T,时段编号为Tnum,TTnum为巷道权值更新时刻。初始时刻Q={V8},U={V1,V2,V3,V4,V5,V6,V7,V9,V10,V11,V12,V13,V14,V15,V16,V17}。节点V9、V15、V16与节点V8相邻,所以W8,9、W8,15、W8,16可以获知,其余节点累计权值均为∞。 步骤2更新遍历节点集和边集。根据模型的筛选指标,从集合E中删除无效边,更新集合V和E。由于图2中E9,7为不可通行路径,在集合E中去掉E9,7,集合V={V1,V2,V3,V4,V5,V6,V10,V11,V12,V13,V14,V15,V16,V17}。 步骤3对未知节点集进行遍历。从U中选出距源点Vi权值最小的节点Vk,将该点从U移到Q中,同时,将该点Vk的权值和对应的路径分别存放到Wik和Pix中。在步骤1的基础上,设集合U中节点V15距源点V8具有最小累计权值W8,16,故Q={V8,V16},U={V1,V2,V3,V4,V5,V6,V10,V11,V12,V13,V14,V15,V17}。 步骤4比较更新邻近节点权值。设节点Vk到邻近子节点Vg的权值为dkg,判断Wik+dkg与Wig的大小,更新i~g的最小权值Wig对应路径Pig。在步骤3的基础上,节点V16的邻近节点包括V17和V8(为突水点排除),由于一开始节点V17的累积权值为无穷大,故此时应当更新W17。 步骤5判断巷道权值是否更新。若到节点k的最小权值Wk>TTnum,表明到达节点k的巷道将经历权值更新。在前4步基础上,当前,Q={V8,V16,V17},U={V1,V2,V3,V4,V5,V6,V10,V11,V12,V13,V14,V15}。集合U中V14具有最小累计权值W14,且W14>TTnum,说明在E17,14巷道权值发生更新。 步骤6计算路径实际累计权值。经过步骤5判断之后,计算实际权值W14=W17+d17,14=32+25=57。 步骤7循环步骤5、6,直至找到突水点Vi到安全节点Vj的最小累计权值Wij结束,即得到最优逃生路径。 一般情况下,突水事故点Vi固定,逃生出口一般至少有3个(主井、副井、风井),因此逃生终点Vj在选取Vj1、Vj2、Vj3的情况下,按照上述算法步骤可分别计算出Vi~Vj的总共至少3条路径。根据具体的矿井突水事故案例,可对其按照路径当量长度进行排序,选取最优的逃生路线。 以W煤矿矿井的1035工作面实际巷道布置图为基础,简化其节点,选出50个关键节点形成巷道网络图(图3)进行实验验证,其中V48、V49、V50是该矿井的井口,将这3个节点设为安全节点。根据该矿井水文地质资料、采掘工程资料得知V1易发生突水,所以将节点V1设为突水点。在未发生突水之前,根据式(8)计算出每条巷道的初始当量长度,如表6所示(限于篇幅只列举部分数据)。 图3 1035工作面巷道网络图Fig.3 Roadway network diagram of 1035 working face 假设V1点发生突水时突水流量恒定为5.86 m3/s,根据文献[22]求得突水从一个节点到另一个节点的漫延时间,再经过无向图宽度优先搜索算法生成突水漫延路线网络图(图4)。 水流下向漫延时间计算公式为 (14) 式(14)中:Lij为巷道初始当量长度,m;Vij为不同巷道内的水流速度,m/s。 水位上向升涨时间计算公式为 表6 巷道结构信息及初始当量长度计算结果(部分)Table 6 Roadway structure information and initial equivalent length calculation results (part ) (15) 式(15)中:V为根据巷道断面与淹没巷道的路径长度计算得到的巷道空间体积,m3;Q为突水流量(恒定),m3/s;Q1为单位设施排水能力(这里暂不考虑)。 表7 巷道水位上升情况(部分)Table 7 Water level rise inroadway (part) 图4 突水漫延路线网络图Fig.4 Network diagram of water inrush spread route 表8 不同巷道的危险性(部分)Table 8 Risk of different roadways (part) 根据巷道的当量长度及突水漫延方向构建巷道加权有向网络图为:设加权有向图G=[V,E,B,C,l(p,tspread)],其中,V为巷道节点的集合,E为节点边的集合,B为巷道节点的标高信息集,C为(Vi,Vj)两点之间更新后的当量长度,l(p,tspread)为水漫延路径集,其中,p为水流经过的节点,tspread为水漫延的时间;使用邻接矩阵来进行存储数据和描述。然后根据以上数据信息,在Python平台上编写程序,模拟在各段时间内,水流可能漫延的巷道,调取巷道数据信息库,修改各段巷道的平均水位高度和平均水流速,重新计算每条巷道的危险性系数及巷道的当量长度。最终用改进Dijkstra算法计算出突水点到3个安全节点的最短路径,然后对这3条路径按照路径当量长度从小到大排序,结果如表9所示。 由于只考虑在同一个工作面工作的矿工人员逃生,人数相对来说不是很多,所以从这3条中选取1条最优的路径作为逃生路径即可,则从突水点到安全节点的最优逃生路径为:V1→V2→V6→V10→V11→V26→V34→V35→V37→V41→V44→V47→V48(图5红色虚线),路径当量长度最短为2 239.58 m;并且本结果也适用于当逃生人员比较多时,同时从三条路径中进行逃生,可有效避免拥堵,提高井下人员的逃生效率。 表9 改进Dijkstra算法的仿真结果Table 9 Simulation results of improved Dijkstra algorithm 图5 1035工作面的最优逃生路径Fig.5 Optimal escape path of 1035 working face 传统Dijkstra算法只适合求解路径权值不变的情况,而无法根据巷道中水位高度及水流速的变化来选择逃生路径,也就是说在本实例中只能求解出特定某T时段下的最优路径,而无法根据整个突水漫延过程来动态选择出最优路径。 假设选取T1(k=1)这个时段下的路径权值,用传统Dijkstra算法来分别求解突水点V1到安全点V48、V49、V50的最优逃生路径结果如表10所示。 表10 传统Dijkstra算法的仿真结果Table 10 Simulation results of traditional Dijkstra algorithm 从表9、表10可知,表10中从突水点V1到安全点V48、V49、V50的最优逃生路径的路径当量长度都比表9中求得的结果小,这是因为在T1(k=1)时段下,突水漫延范围相对较小,某些巷道的危险系数也较小,在巷道静态因素不变的情况下,路径当量长度也较小,所以选择的最优逃生路径与表9也不相同。 为了体现该优化算法的动态选择性,根据表9得到的最优结果,以到达安全节点V48的逃生路径动态选择为例,分别选取T12(k=12)、T13(k=13)、T14(k=14)3个时段下运用改进的Dijkstra算法仿真结果进行对比,结果如表11所示。 表11 T12、T13、T14时段下改进Dijkstra算法的前2条最优逃生路径仿真结果Table 11 Simulation results of the former two optimal escape paths of improved-Dijkstra algorithm at T12,T13,T14 比较表9~表11可知,传统Dijkstra算法仅仅只能反映当前时间段下的最优路径,不能根据突水灾害实际情况动态选择出合理的逃生路径,而表9得到的最优逃生路径是根据表11不同时段下巷道危险性程度进行动态选择的,得到的路径更加安全、可靠,改进的Dijkstra算法恰好弥补了传统算法的不足。因此,本文模型以及改进的算法比传统的模型和传统的Dijkstra算法在矿井突水动态环境中求解最优逃生路径更具优势。 (1)为了更符合矿井突水灾害逃生路径选择的实际情况,同时考虑水位高度和水流速对人体稳定性的影响,并据此提出一种危险系数的计算方法,优化传统最优逃生路径数学模型。 (2)通过划分时间段来估算随时间变化的水位高度与水流速,从而计算各时间段内的预测危险系数,进而得到巷道当量长度,以此动态的选择最优逃生路径。 (3)改进后的Dijkstra算法,根据划分的时间段求得对应的危险性权重,从而更新每条巷道当量长度的邻接矩阵,突破了传统的Dijkstra算法不能用于动态路径搜索的不足,使得在矿井突水最优路径的选择中更具有精确性与实用性。通过仿真实验分别求得了从突水点V1到3个安全地点V48、V49、V50的最优逃生路径:①V1→V2→V6→V10→V11→V26→V34→V35→V37→V41→V44→V47→V48;②V1→V3→V5→V9→V13→V14→V17→V18→V26→V34→V40→V49;③V1→V2→V6→V10→V11→V26→V34→V35→V36→V39→V42→V45→V46→V50;然后对这3条路径按照路径当量长度从小到大排序,选取其中一条最优的路径,即V1→V2→V6→V10→V11→V26→V34→V35→V37→V41→V44→V47→V48,路径当量长度为2 239.58 m作为该工作面的突水逃生路径。 (4)此项研究不仅适用于矿井突水动态最优逃生路径的选择,还可以应用于地铁隧道透水事故等逃生路径动态选择中,具有普遍适用的意义。


2.4 巷道初始当量长度的计算


2.5 目标函数
3 改进的Dijkstra算法
4 实例分析
4.1 基于Python仿真实验


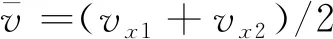


4.2 结果比较分析


5 结论
