工业机器人动力学参数分步辨识与零力控制示教

方骏玮，王斌锐，谢胜龙，任海军

（1.中国计量大学机电工程学院，浙江 杭州 310018；2.杭州新松机器人自动化有限公司，浙江 杭州 311200）

1 引言

机器人可代替人工完成高负荷、重复性任务，提高生产效率，工业领域应用需求量大。现有的机器人示教大多采用示教盒示教，示教过程复杂，精度较低，且对操作者技术水平要求高，限制了机器人推广应用。尤其是在对示教轨迹精度要求高的领域，如喷涂、打磨等，采用示教盒示教时存在着工作量大、效率低下的问题。为满足现代工业复杂多变的特点，直接示教逐渐引起了学者们的重视。直接示教是指操作者直接拖拽机器人末端，以末端沿着工作轨迹运动，形成机器人整套动作。该示教方法能大大简化机器人操作流程，提高企业生产效率。

当前在直接示教领域研究的重点是在无传感器的情况下采用控制算法实现直接示教，其中最为典型的一种方法是零力控制方法［1］，它是促使机器人顺应外力作用，使得其运动如同不受重力和摩擦力等外力作用的一种控制方法。目前常用的零力控制方法主要基于重力与摩擦力补偿［2-3］。实际上，当示教速度增加时，机器人因运动引起的惯性项增加，从而导致机器人示教柔顺性变差。因此，在零力控制器的设计中有必要考虑惯性项的影响。零力控制的关键在于准确地补偿机器人所受的重力矩以及摩擦力矩。因此动力学模型的精确性对提高示教过程的柔顺性至关重要。常用的获取机器人动力学参数的方法有CAD软件测量法和动力学参数辨识法［4-6］。由于前者忽略零件的加工、装配等误差而与真实情况存在很大偏差。因此目前主要采用动力学参数辨识方法。然而，当关节数目超过4个后，由于动力学模型复杂程度急剧增加，准确的动力学参数往往很难获取。为此，文献［7］提出了一种工业机器人动力学参数分步辨识新方法。该方法在简化辨识方程的同时，减小了计算量，提高了辨识精度。但是，由于只做了连杆的分步，而分步后连杆的动力学模型依旧十分繁冗，在对系数矩阵的条件数进行优化时依然存在较大难度。

这里所设计的零力控制器在传统零力控制器的基础上增加了惯性力补偿并应用于机器人免力矩传感器直接示教。同时，针对6轴机器人动力学模型参数辨识复杂的特点，提出了一种新的分步参数辨识方法以降低计算量，提高参数辨识效率。最后，以一种6轴机器人为研究对象验证了该动力学参数分步辨识方法的可行性和所提零力控制方法的有效性。

2 机器人动力学建模

机器人零力控制的基础是其动力学模型，这里采用牛顿-欧拉法建立机器人的动力学模型：

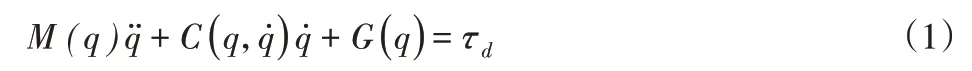
研究表明，存在一组依赖于机器人惯性参数的特征向量，能将非线性的机器人动力学方程转换成如下线性化形式［8］：

令机器人关节数目为n，则Φd为n× 10n维观测矩阵，Φd与机器人惯性参数无关；pd为10n× 1 维的机器人惯性参数向量，对于机器人连杆i而言，其自身连杆的惯性参数向量pdi的具体形式为：

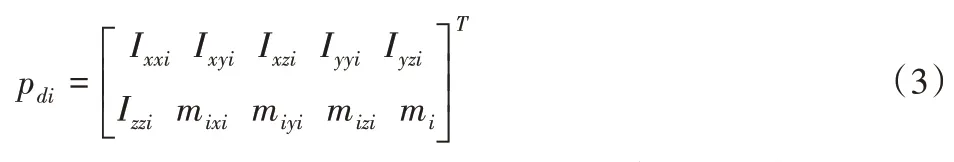
式中：Ixxi、Ixyi、Ixzi、Iyyi、Iyzi、Izzi—连杆i相对于坐标系i原点的惯性张量；mi—第i个连杆的质量；mixi、miyi、mi zi—连杆i相对于坐标系i原点的一阶惯量矩；xi、yi、zi—连杆i的质心坐标。

上述式（1）和式（2）为不考虑摩擦情况下机器人理想的动力学方程。然而在机器人实际工作过程中，摩擦对机器人的动态特性不可忽视。这里引入经典的库伦黏滞摩擦建立机器人关节的摩擦力矩模型：

式中：τf—机器人关节摩擦力矩；

fc和fv—库伦摩擦系数和黏滞摩擦系数。

结合式（2）和式（4），即可得到考虑摩擦的机器人线性化动力学方程：

式中：Φs—n×12n维观测矩阵为12n×1维的机器人惯性参数向量，对于具体的连杆i，有：

理论研究表明观测矩阵Φs总是不满秩的，意味着向量ps中并不是所有连杆的惯性参数都会对机器人的关节力矩产生作用［9］。为此，需要通过一定的线性变换对机器人动力学参数进行重组得到一组最小惯性参数。重组后只含有最小惯性参数的线性化动力学模型可表示为：

3 机器人动力学参数辨识

3.1 参数辨识方法研究

已知式（7）所述的线性动力学模型，机器人动力学参数的辨识问题即转变成方程组的求解问题。驱动机器人按既定的辨识轨迹运动，确定采样周期，取得多个不同位置下的角度、角速度、角加速度和力矩值，记采样的次数为N（为防止噪声对测量值的影响，N一般取值较大），则可得如下超静定方程：

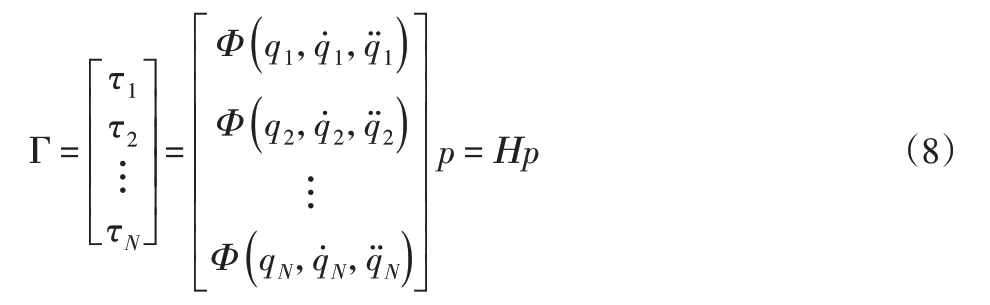
式（8）为机器人动力学参数的辨识方程，其中Η为nN×(p+2n)维观测矩阵，称Η为辨识方程的系数矩阵；Γ为nN×1维力矩向量。

对于该超静定线性方程，采用加权最小二乘法估算机器人惯性参数向量P，通过对测量噪声协方差的逆矩阵进行加权，可得P的估计值为：

Σ—N×N的力矩协方差矩阵，即加权矩阵。

由于6自由度工业机器人动力学模型复杂，辨识方程系数矩阵维度高，辨识过程计算量大，很难直接采用上述辨识算法进行参数估计。为此，这里根据机器人各关节驱动力矩数值的差异，将待辨识的研究对象分为两类，第一类研究对象为各轴的驱动力矩差异较大的机器人，第二类研究对象为各轴驱动力矩区别不大的机器人（如协作机器人）。

对于第一类研究对象，其1-3轴的驱动力矩远大于4-6轴的驱动力矩，因此1-3轴的惯性参数在数值上同样要远大于4-6轴惯性参数，同时4-6轴的惯性参数对1-3轴影响不大，故可先忽略4-6轴的影响，对机器人1-3轴进行动力学建模并辨识出1-3轴的惯性参数，在此基础上再辨识4-6 轴的惯性参数。这是文献［7］中介绍的分步参数辨识方法。

实际上，由机器人动力学模型（1）与摩擦模型（4）可知，当机器人处于静止状态时，驱动力矩主要用于克服机械臂的重力矩以及库伦摩擦力矩，而各连杆的重力矩只与连杆质量及其一阶质量矩相关，所受的库伦摩擦由库伦摩擦系数决定。因此可以将动力学参数分为两组，第一组是与重力矩及库伦摩擦力矩相关的质量、一阶质量矩以及库伦摩擦系数，第二组是与机器人转动惯量相关的惯性张量以及与粘滞摩擦力矩相关的粘滞摩擦系数。

因此，可在上述参数分步辨识方法的基础上做进一步细化处理，这里所设计的动力学参数分步辨识流程，如图1所示。

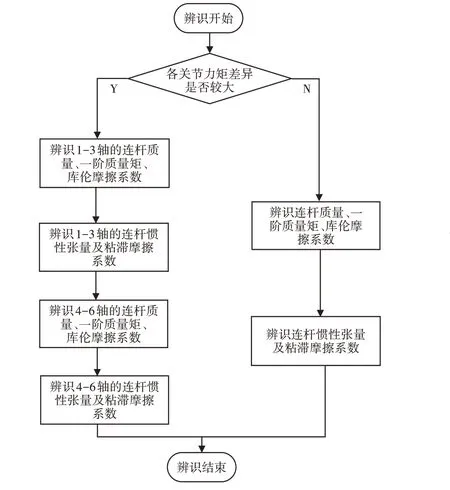
图1 参数分步辨识流程图Fig.1 Parameter Classification Step Identification Flow Chart

关于第一类研究对象的动力学参数分步辨识方法如图1左侧流程所示，其具体辨识步骤如下：

（1）辨识1-3轴中各连杆质量、一阶质量矩以及库伦摩擦系数；（2）辨识1-3轴中各连杆惯性张量与各关节的黏滞摩擦系数；（3）辨识4-6 轴中各连杆质量、一阶质量矩以及库伦摩擦系数；（4）辨识4-6轴中各连杆惯性张量与各关节的黏滞摩擦系数。

而待辨识的对象为各个关节驱动力矩区别不大的机器人时，则上述参数分步辨识方法退化为图1中右侧所示的两步参数分步辨识法，即先辨识各连杆的质量、一阶质量矩、库伦摩擦系数，再辨识各连杆惯性张量与各关节的黏滞摩擦系数。采用以上分步辨识方法，充分降低了计算过程的矩阵维度，减少了计算量，为实现多自由度机器人参数辨识提供可行的方法。

3.2 激励轨迹设计与优化

在进行机器人动力学模型参数辨识前，需要合理地选择激励轨迹，以充分激励待辨识系统，进而精确辨识出动力学模型中的未知参数［10］。

为避免机器人在运动轨迹节点处的“跳变”现象，这里采用傅里叶级数作为机器人的激励轨迹，机器人的激励轨迹可表示为：

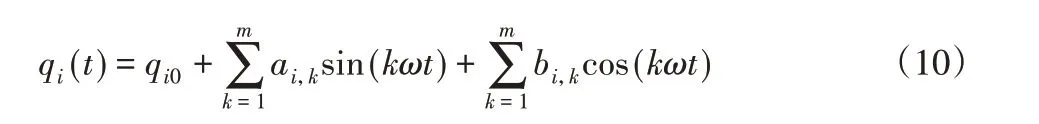
式中：t—轨迹运行时间；ω—轨迹基础频率，这里取0.2πHz；qi0—第i个关节的位置补偿量；qi—第i个关节的位置；ai，k和bi，k—正余弦分量的幅值；m—傅里叶级数的次数，这里取m=5。

实际辨识中，系数矩阵H的条件数越小，最后的辨识结果受采样值噪声影响越小。H的条件数则由激励轨迹的参数qi0、ai，k和bi，k决定。以系数矩阵H的最小条件数为优化目标，机器人的关节限位为约束条件，采用相关的优化算法可得到最优激励轨迹的决策变量qi0、ai，k和bi，k。

4 零力控制研究

零力控制算法的本质是实时补偿机器人关节所受的重力矩和摩擦力矩，传统的零力控制器在力矩控制模式下输出的力矩τact为如下形式：

结合式（1）可知，该控制器补偿了示教过程中机器人的重力与摩擦力，操作者施加的外力需要克服机器人关节的惯性力项M(q)、科氏力与向心力方可拖动机器人运动，即：

式中：τF—操作者示教过程中施加的操作力项。

考虑到在机器人的示教过程中，当示教速度有明显的改变时，机器人关节所受的惯性力项数值会较大。为了提高拖动示教的柔顺性，这里提出了一种改进的零力控制方案，该方案在传统零力示教方案基础上，进一步进行了机器人惯性力矩的补偿，其控制方案，如图2所示。

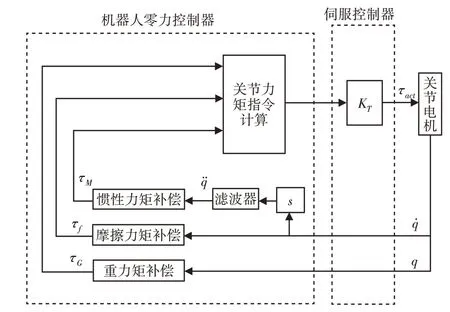
图2 改进零力控制框图Fig.2 Improved Force-Free Control Block Diagram

此时机器人关节的输出力矩为：

式中：τM=M(q)—机器人惯性力矩。

经过上述补偿后，操作者在拖动机械臂进行示教的过程中，施加的操作力τF仅需克服机器人的科氏力项和向心力项即可，即：

从而增加了拖动示教过程中的柔顺性。这里，由于无法直接读取机器人关节电机的加速度，因此需要先对机器人关节速度进行差分处理，再将差分结果进行低通滤波处理后得到机器人的角加速度。

5 实验验证

5.1 实验平台

为验证这里提出的分步参数辨识方法和零力控制算法的有效性，这里以新松SR4C工业机器人为研究对象，基于自主研发的驱动控制系统开展实验验证研究。

实验所用机器人，如图3所示。机器人末端法兰装有ATI六维力/力矩传感器，传感器应变片一侧装配机器人示教手柄。实验中操作者拖动手柄带动机器人运动进行示教，ATI六维力/力矩传感器实时测量示教过程中的示教力，其x轴、y轴与z轴的方向由传感器定义。

图3 实验平台Fig.3 Experiment Platform

5.2 参数辨识实验

根据上述的参数分步辨识方法，机器人3轴与6轴均为分步辨识的末端连杆，通过比较辨识结果的数值差异，可证明分步辨识的可行性，因此这里给出机器人3轴与6轴的辨识结果，如表1所示。表中上标b表示重组后的最小惯性参数。

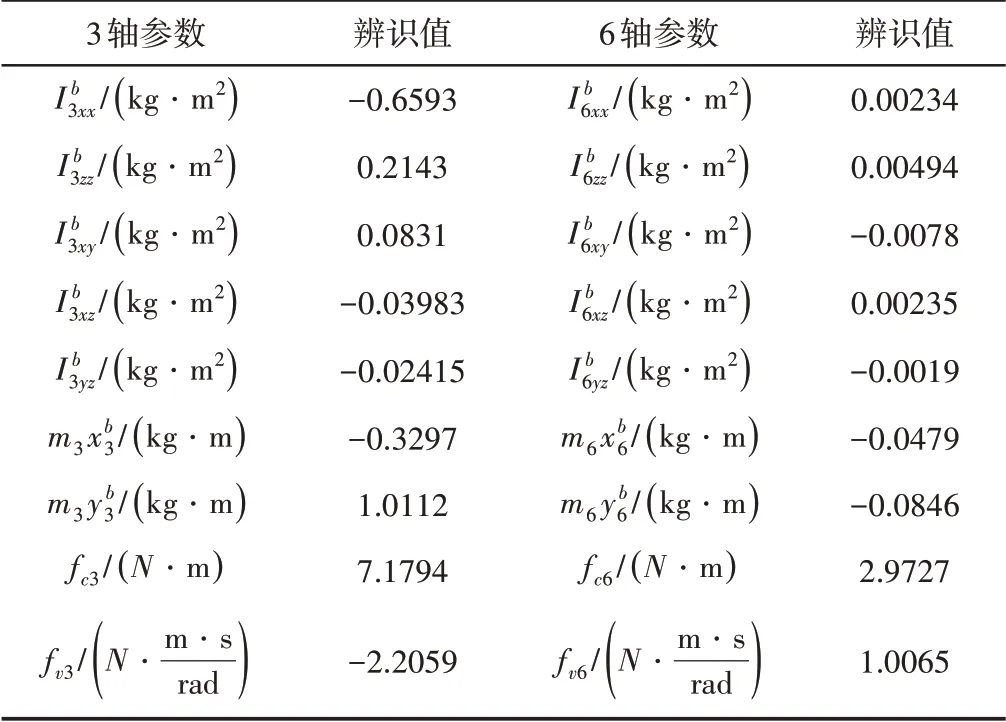
表1 机器人3轴、6轴动力学参数值Tab.1 Robot 3-Axis，6-Axis Dynamic Parameter Values

机器人在空载情况下，各关节实际力矩、辨识模型预测力矩、CAD模型预测力矩，如图4所示。从图4中可以看出，各关节辨识模型预测力矩对实际力矩始终保持相同的变化趋势，显示出良好的跟随性，且6个关节的误差均在小范围内波动，说明该辨识方法所辨识出的动力学参数具有较高的精度。与之相反，CAD模型预测值虽然也能对测量力矩保持相同的变化趋势，但是偏差非常大。产生这种现象的原因有：

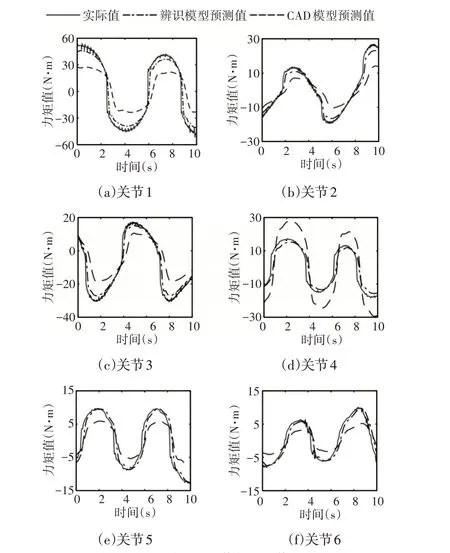
图4 关节测量值与预测值Fig.4 Joint Measurements and Predicted Values

（1）CAD 建模时材料的分布特性与实际的铸造零部件存在偏差；

（2）零部件的加工与装配误差导致惯性项存在较大偏差；

（3）机器人工作过程中因摩擦导致零件接合处产生磨损和间隙；

（4）CAD模型没有计入摩擦的影响。

上述诸多因素使得连杆参数和机器人动力学特性发生变化，进而使得CAD模型的预测值与实际测量值产生较大偏差。

5.3 机器人牵引实验

实际牵引示教过程，如图5所示。机器人在无力矩补偿、仅有重力矩和摩擦力矩补偿以及增加惯性力矩补偿三种情况下示教过程中的操作者的示教力曲线，如图6所示。

图5 牵引操作示意图Fig.5 Traction Operation Diagram

由图6（a）可见，无力矩补偿时，由于需要同时克服机器人运动过程中的重力、摩擦力、惯性力和科氏力等力矩的作用，操作者需要施加很大的力才能拖动机器人的各个关节进行示教运动，其x和y方向示教力的幅值最高能达到100N 以上。图6（b）表明，当增加重力矩以及摩擦力矩补偿后，操作者施加的示教力主要用于克服机器人惯性力以及摩擦力，其操作力显著减小，示教力的幅值降到30N以下，示教过程中牵引力越小，则视示教过程的柔顺性越好，因此传统的零力控制方法能明显提高示教过程的柔顺性。图6（c）为增加惯性力矩补偿后的示教力曲线，与图6（b）相比，其x和y方向的示教力显著减小，其幅值为传统零力控制的71.4%，可见这里所提出的零力控制方法能显著增加示教过程的柔顺性。

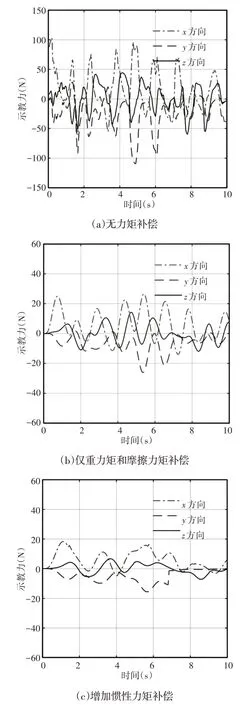
图6 示教力曲线Fig.6 Teaching Force Curve

6 结论

（1）设计了一种工业机器人动力学参数分步辨识的新方法，可降低辨识方程系数矩阵的维度，减少计算量，提高辨识效率。

（2）在传统的零力控制算法基础上加入机器人关节惯性力矩项补偿，进一步提高了拖动示教过程的柔顺性。

（3）对所提出的零力控制方法开展了实验研究，实验结果表明这里所提出的零力控制方法能显著减小示教过程中的操作力，使得示教过程更为轻便灵活。