换热器板束矫直过程试验与数值研究

唐文献，张可华，张 建

（江苏科技大学机械工程学院，江苏 镇江 212003）

1 引言

换热器是一种结构紧凑、质量轻巧的换热设备，在热能领域以其高效的换热效率，广泛应用在石油化工、家电、车辆、动力工程和机械等领域［1］。常见的换热器基本组成单元为板束，板束由上板、翅片和下板通过真空钎焊工艺焊接而成。受翅片成型质量不稳定、板束组装中翅片间距分布不均等因素影响，板束在经真空钎焊和出炉冷却后易产生翘曲现象，过大的翘曲造成板束平直度差，影响板束后工序的并排组装。在板束制造领域，平直度检测是钎焊后板束质量检测的重要内容［2］，因此如何通过矫直技术来提高板束加工后的平直度已成为板束加工中需要迫切解决的问题。

目前，矫直技术的研究多集中在对板材、棒材等具有规则几何形状的工件矫直研究，研究方法主要有理论计算、有限元模拟和实验研究。文献［3］通过解析法研究了压下量对中厚板残余应力的影响规律，得出适当增加压下量可以降低板材内部的残余应力；文献［4］利用有限元分析软件ABAQUS 对二辊矫直过程进行数值模拟，分析了棒材矫直后的应力、应变和平直度的分布规律，得出数值模拟结果和现场数据基本吻合。文献［5］通过Work⁃bench LS-DYNA 软件对大型H 型钢矫直过程进行数值模拟，得出矫后残余应力值最小且分布状态合理的最佳矫直规程。文献［6］通过解析法和实验法对棒材二辊矫直过程进行研究，分析矫直机的辊偏角和上下辊的转速对矫直效果的影响。文献［7］利用有限元数值模拟，分析了H钢在矫直过程中其截面上的应力、应变演变规律。文献［8］利用解析法和有限元法研究了双金属板中性层偏移对矫直力精度的影响。上述文献分析的板材、棒材和H型钢结构简单，对其矫直分析研究较多，但对结构复杂的换热器板束的矫直机理研究较少，因此需要对板束矫直机理作具体分析。

以换热器板束矫直过程为研究对象，根据板束结构参数进行板束几何建模与矫直有限元分析，再利用板束矫直实验验证有限元模型的正确性；其次，根据有限元矫直过程的模拟，分析板束在矫直中和矫直后各路径上的应力、应变分布规律；最后，分析矫直参数中的上辊压下量和板束初始弧高对矫后残余应力、塑性应变和矫后平直度的影响规律，为板束矫直设备开发提供理论依据。

2 材料与方法

2.1 几何模型

板束单元通过专用组装工具将上板、翅片和下板组装并固定在一起，然后通过真空钎焊工艺焊接而成。板束上板和下板均为平直薄板，厚度均为0.7mm，翅片外形为波浪形状态，由专用的翅片成型机冲制而成，翅片厚度为0.3mm，节距为1.6mm，翅高为8.2mm。组装好的板束工件长为640mm，宽为15mm，高为9.6mm，板束工件几何尺寸示意图和实物图，如图1所示。

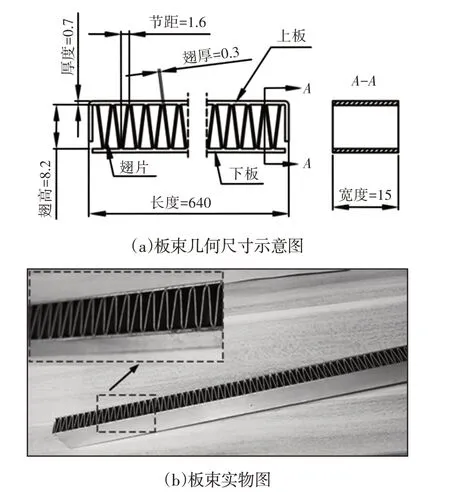
图1 板束组件Fig.1 Plate Bundle Assembly

2.2 材料属性

板束的上板、下板和翅片均为铝箔制成，为获得铝箔的材料参数，对铝箔进行拉伸实验。因铝箔宽度较小，所以根据GB/T228.1-2010 的规定采用不带头试样，试样宽度等于工件宽度。采用板束单元的上板制作拉伸试样，试样中间粘贴应变片，以测量铝箔泊松比，铝箔拉伸试样，如图2（a）所示。对4个铝箔试样进行拉伸实验，4个试样编号分别为ES1、ES2、ES3、ES4，通过拉伸实验获得的铝箔材料参数为：弹性模量均值为68GPa，泊松比均值为0.32，屈服强度均值为152.5MPa，拉伸应力应变曲线，如图2（b）所示。

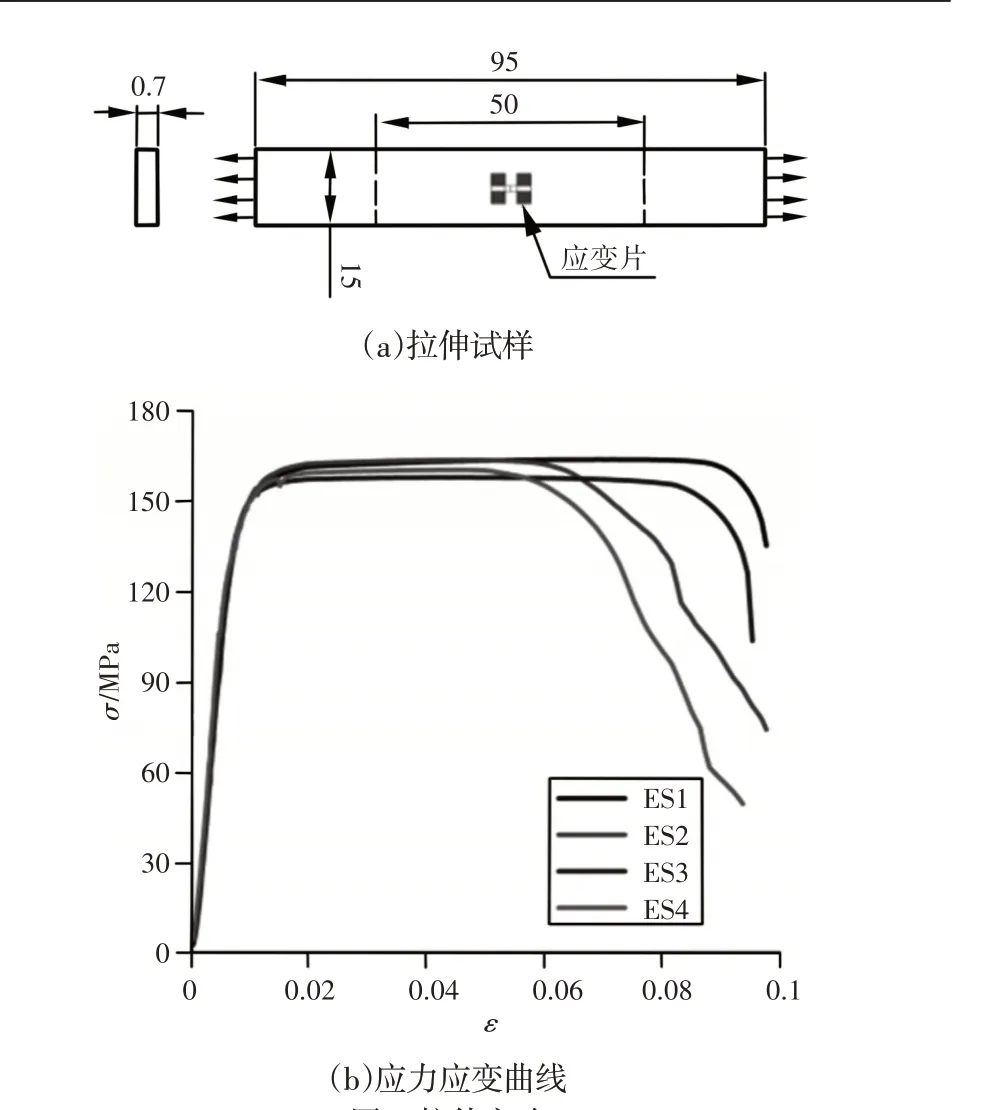
图2 拉伸实验Fig.2 Tensile Test

2.3 板束矫直有限元模型

板束矫直有限元模型可简化为上排矫直辊、下排矫直辊、板束，在板束建模中，采用百分表测量80个板束上表面的平直度数据，根据测得的板束平直度数据，统计出板束的初始弧高分布。结果表明，板束初始弧高分布集中在（0.5～0.7）mm 之间，故初选0.5mm弧高的板束作为其几何模型。采用11辊平行辊式矫直方案，上排矫直辊数量为5个，下排矫直辊数量为6个。由于板束模型相对于板束宽度方向中心线是完全对称的，为了缩短计算时间，只选取模型沿板束宽度方向的一半作为研究对象，且设置模型质量缩放系数为200［9］。采用理想弹塑性模型定义材料参数，板束自由度约束为可沿X、Y方向移动，其余自由度限制。矫直辊辊径为40mm，矫直辊设置为解析刚体［10］可绕自身Y轴旋转，其余自由度限制。

板束和矫直辊的接触方式为硬接触，摩擦系数为0.3。板束网格划分采用C3D8R网格模型，网格单元总数为310862个。分析步中设置下排矫直辊转速为3rad/s，上排矫直辊随动，此有限元矫直过程为准静态过程，在Abaqus中建立的板束矫直模型，如图3所示。

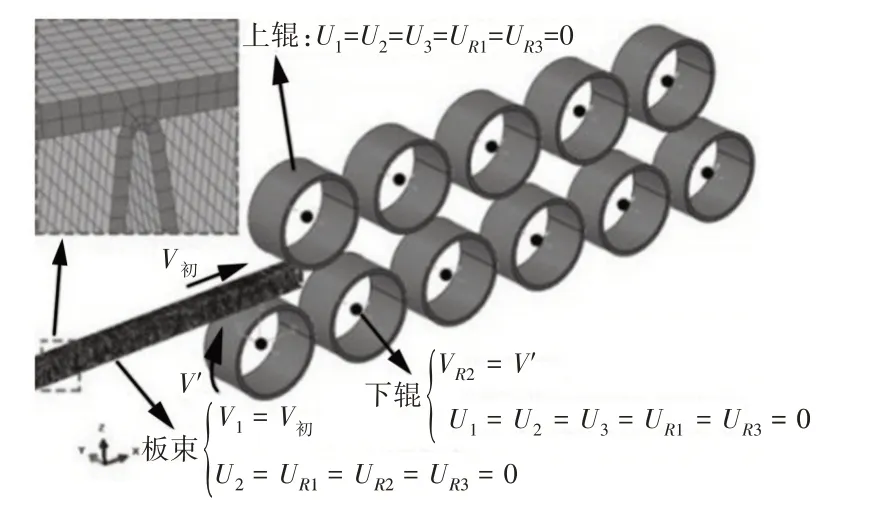
图3 网格模型和边界条件Fig.3 Grid Model and Boundary Conditions

2.4 板束矫直实验

板束矫直实验采用11辊矫直机，矫直机辊径为40mm，上排辊数为5辊，下排辊数为6辊，板束工件高9.6mm，压下量为0mm时的上下排辊外径表面间距为9.7mm。通过安装标准厚度的垫片来调节上排辊子的压下量，通过安装标准厚度的隔板来调节水平辊距的大小，采用步进电机进行矫直速度调节。矫直过程为：先用百分表测量板束矫直前的平直度数据，再根据矫直工艺参数调节矫直机的压下量和辊距，设置好电机的转动速度，然后启动电机，将板束放入矫直机入口开始矫直作业，最后取出矫直后的板束，关闭电机，并测量板束矫直后的平直度数据，矫直实验流程，如图4所示。

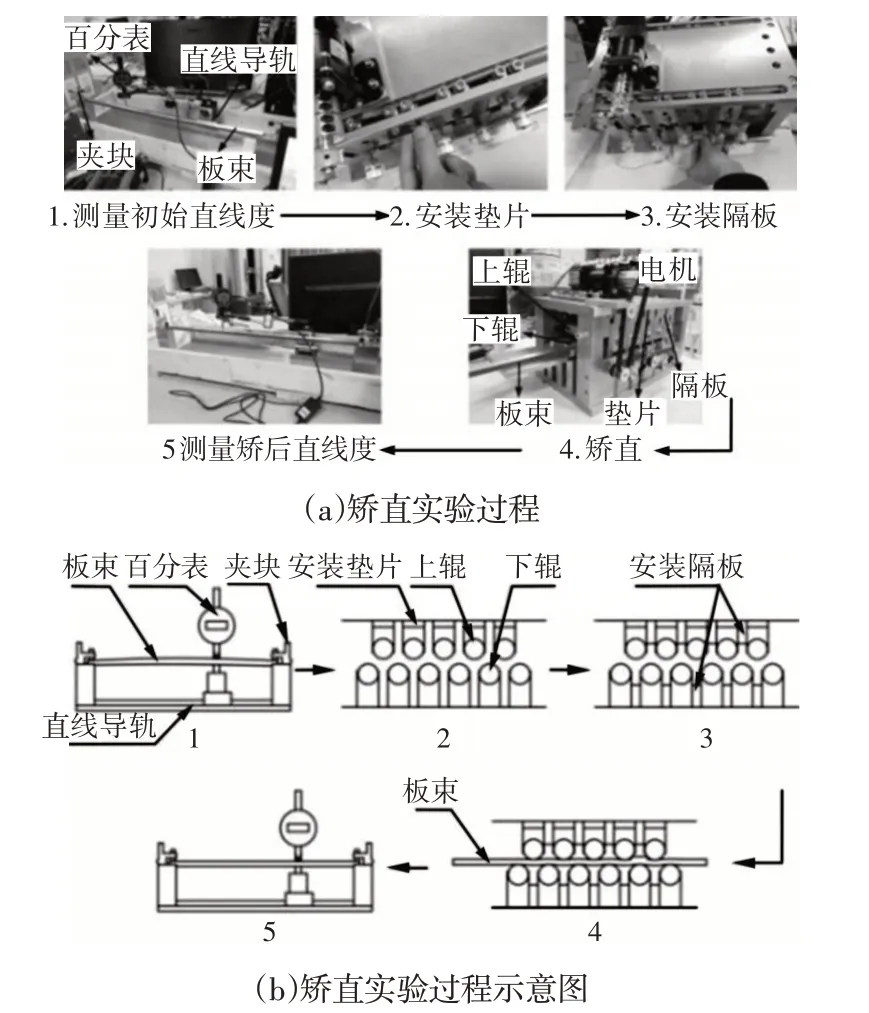
图4 实验过程Fig.4 Experimental Procedure

3 结果分析与讨论

3.1 模型验证

为了验证有限元模型的准确性，验证一组矫直工艺参数下的有限元仿真结果与实验结果关于板束矫后平直度的对比。实验矫直工艺参数为：上辊压下量为0.2mm，辊距为52mm，矫直速度为60mm/s，板束初始弧高为0.5mm，有限元仿真矫直后的板束平直度曲线和实验矫直后的板束平直度曲线，如图5所示。

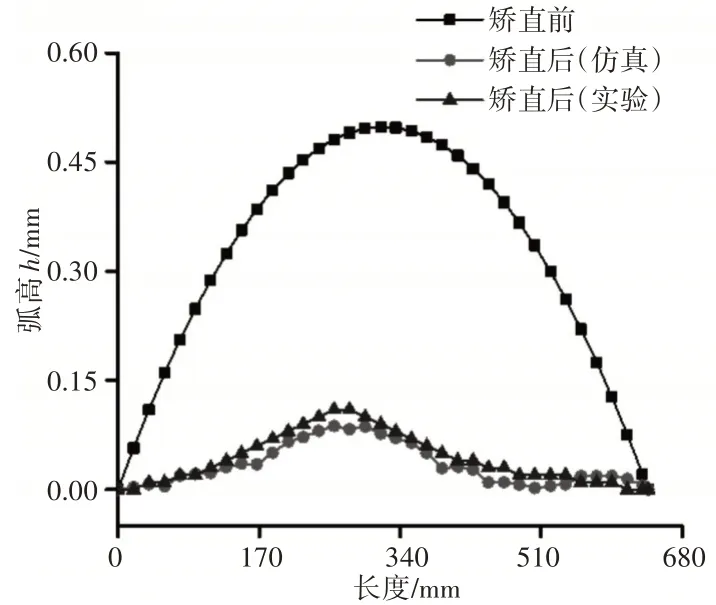
图5 仿真与实验矫后平直度对比Fig.5 Comparison of Simulated and Experimental Straightness

由图5可知，仿真后的板束轮廓变化趋势和实验后板束的轮廓变化趋势基本吻合，仿真后的板束平直度为：0.137mm/m，实验后的板束平直度为：0.172mm/m，二者平直度相差仅2.03%，说明了有限元模型与实验吻合良好，有限元模型较准确。

3.2 板束矫直应力分析

以初始弧高为0.5mm的板束矫直过程为分析对象，通过有限元仿真来分析矫直中和矫直后板束各路径上的应力分布规律。矫直工艺参数为：压下量为0.2mm，辊距为52mm，矫直速度为60mm/s，板束在矫直中和矫直后的应力分布，如图6所示。

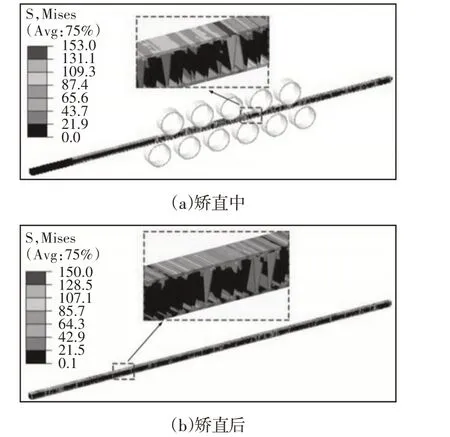
图6 板束矫直应力分布Fig.6 Straightening Stress Distribution of Plate Bundle

由图6（a）可知，当板束完全进入矫直辊后，板束上下表面发生塑性变形，最大应力达到铝箔的屈服极限。在矫直区域内，应力分布在板束长度方向上呈现高低起伏的波浪形状态，应力分布在板束宽度方向上基本保持一致，应力分布在板束厚度方向上呈现由大变小，再由小变大的规律。由图6（b）可知，当板束脱离矫直辊时即矫直完成后，此时的应力为矫直后的残余应力，矫直后的残余应力在板束长度、宽度、厚度方向上的分布规律与矫直中的应力在板束长度、宽度、厚度方向上的分布规律一致。现提取矫直后板束长度方向的上表面一路径绘制其残余应力分布图，如图7所示。

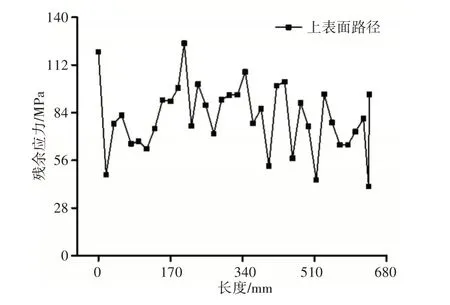
图7 板束上表面路径残余应力分布Fig.7 Residual Stress Distribution along the Surface Path of Plate Bundle

由图7可知，上表面路径的应力分布呈高低起伏的波浪形状态，这与图6（b）中板束沿长度方向的应力分布规律一致。板束沿长度方向的中部路径、下表面路径的残余应力分布规律与图7上表面路径的残余应力分布规律相似，中部路径、下表面路径的残余应力分布数据，如表1所示。

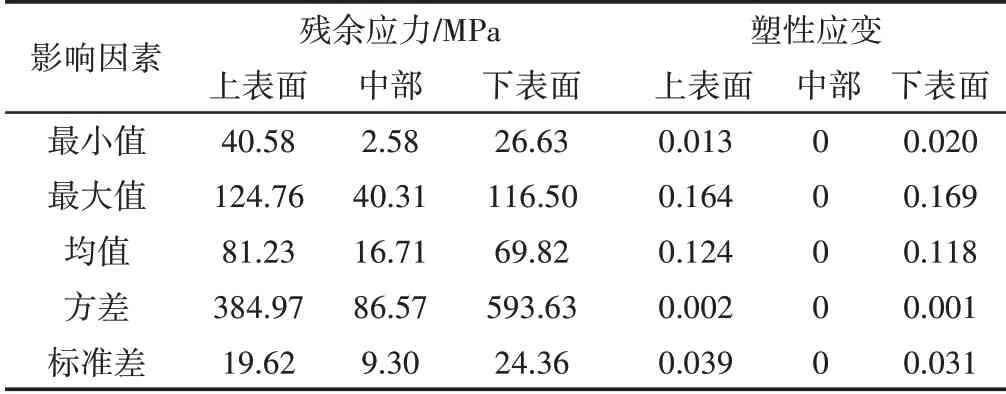
表1 不同路径下的残余应力和塑性应变数值Tab.1 Residual Stress and Plastic Strain Values under Different Paths

3.3 板束矫直应变分析

板束在矫直中和矫直后的应变分布，如图8所示。当板束完全进入矫直辊后，如图8（a）所示，在矫直区域内板束等效塑性应变较大，等效塑性应变分布沿板束长度方向呈现高低起伏的波浪形状态，沿板束宽度方向基本保持一致，沿板束厚度方向呈现由大变小，再由小变大的规律。当板束脱离矫直辊时即矫直完成后，如图8（b）所示，除板束两端没有明显的塑性应变外，板束其余区域内均显示有明显的塑性应变，这表明板束在刚进入矫直辊的咬合过程中，仅发生弹性变形，随着板束不断运动至矫直辊中，塑性变形发生，当板束运动至即将脱离矫直辊时，此段板束也仅发生弹性变形。现提取矫直后板束长度方向的上表面一路径绘制其塑性应变分布图，如图9所示。由图9可知，上表面路径的塑性应变分布为两端区域数值小，中间区域数值大，且数值呈现高低起伏的波浪形分布，这与图8（b）中的塑性应变分布规律一致。板束沿长度方向的中部路径、下表面路径的塑性应变分布规律与图9的上表面路径的塑性应变分布规律相似，中部路径、下表面路径的塑性应变分布数据，如表1所示。

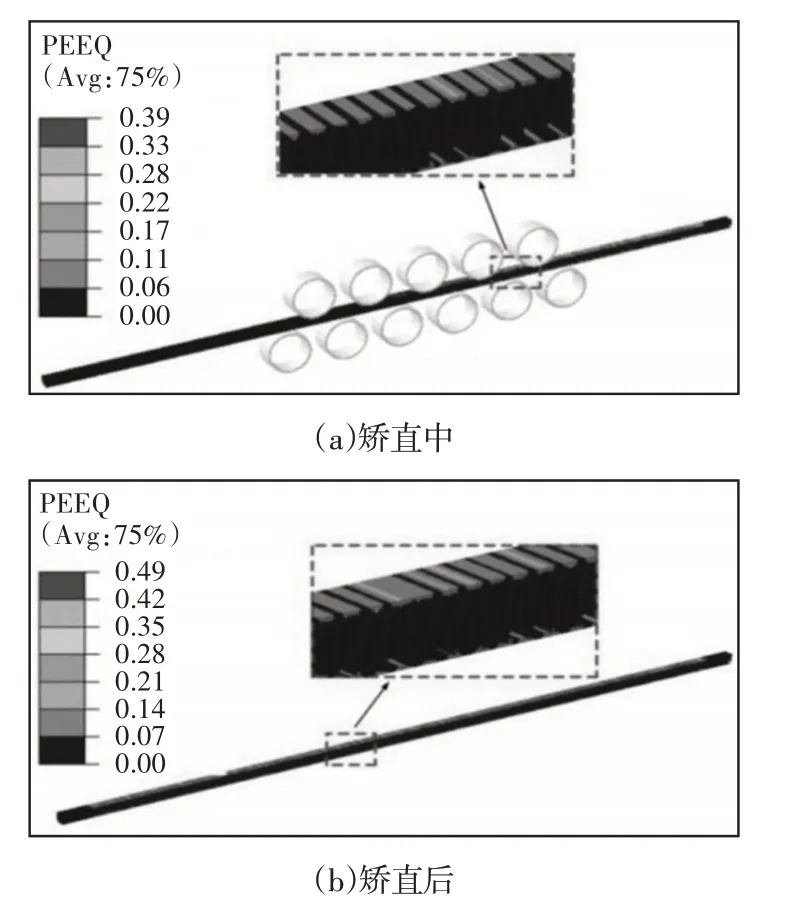
图8 板束矫直等效塑性应变分布Fig.8 Equivalent Plastic Strain Distribution of Plate Bundle Straightening

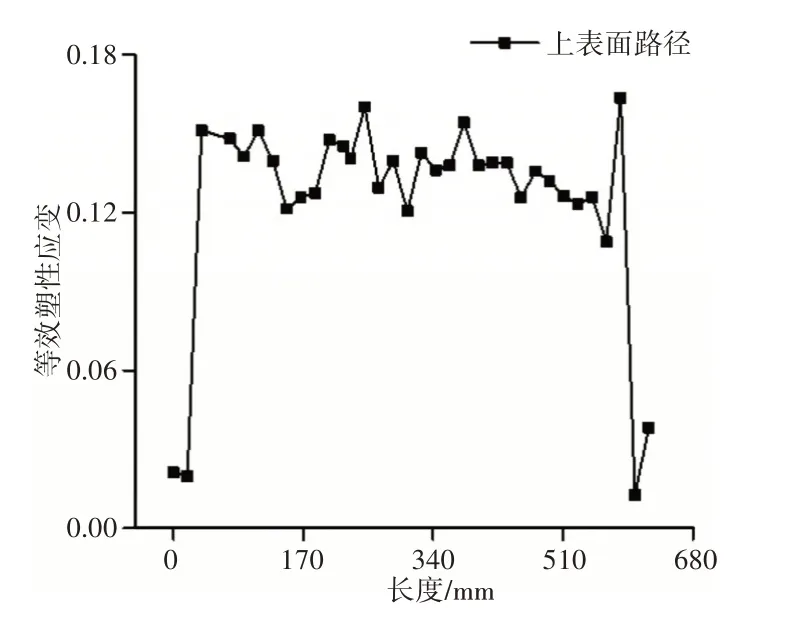
图9 板束上表面路径塑性应变分布Fig.9 Plastic Strain Distribution along the Surface Path of Plate Bundle

3.4 相关参数对残余应力和塑性应变的影响

在板束矫直作业中，板束的矫直效果由矫直后的残余应力、塑性应变的大小和波动范围决定，通过板束矫直后的平直度曲线体现出来。对矫直效果影响较大的因素有矫直工艺参数的选取和板束的初始平直度大小。矫直工艺参数中的上辊压下量对矫直效果影响显著，板束初始不平度由板束初始弧高决定，因此选取不同的压下量和板束初始弧高，来研究压下量和弧高变化对残余应力和塑性应变的影响规律。提取板束上表面沿长度方向路径的残余应力和弧高数值，绘制压下量对板束矫后残余应力和平直度影响规律曲线，如图10所示。

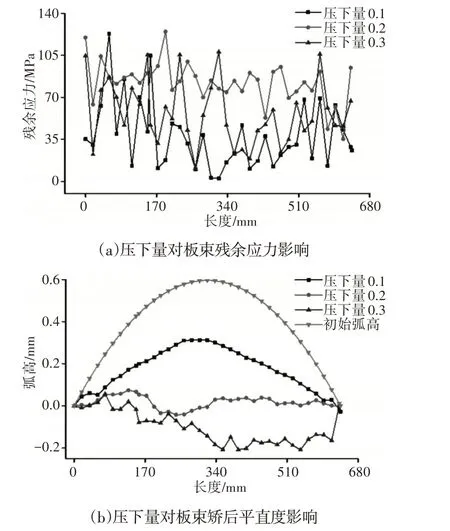
图10 压下量对板束残余应力和矫直效果影响Fig.10 Influence of Reduction on Residual Stress and Straightening Effect of Plate Bundle

由图10（a）可知，上辊压下量为0.1mm和0.3mm时板束矫后残余应力均值较小但波动较大，残余应力波动较大则板束矫后易反弹，矫直效果不稳定；压下量为0.2mm时，板束的残余应力分布较均衡，波动范围较小，说明矫直后板束稳定性好；由图10（b）可知，当压下量为0.2mm时，矫直后的板束平直度最好，说明选取压下量为0.2mm时的矫直效果最理想。不同压下量对板束矫后塑性应变的影响规律与图10（a）相似，现提取不同压下量和不同弧高影响下的板束长度方向上表面路径的残余应力、塑性应变数值，对得到的残余应力和塑性应变数值进行数理统计，统计结果，如表2、表3所示。

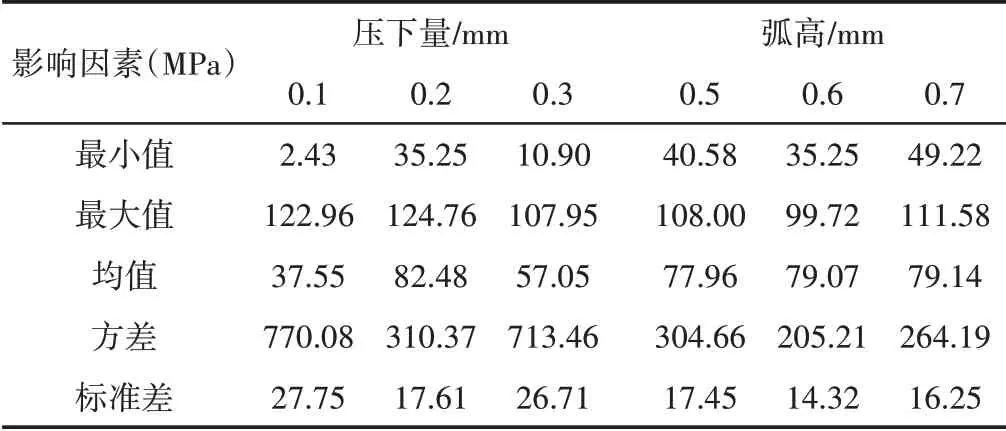
表2 不同压下量和初始弧高对残余应力影响Tab.2 Effect of Different Reduction and Initial Arc Height on Residual Stress

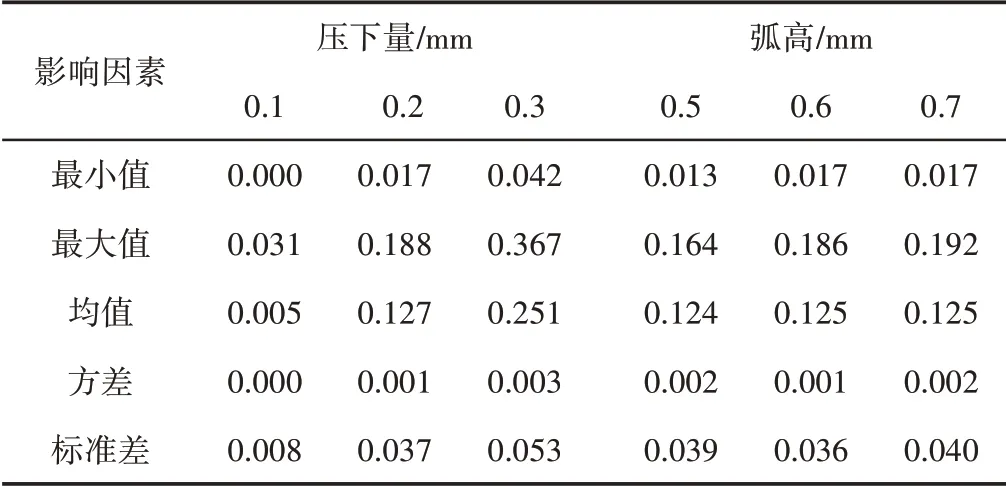
表3 不同压下量和初始弧高对塑性应变影响Tab.3 Effect of Different Reduction and Initial Arc Height on Plastic Strain

由表2 和图10（a）可知，压下量为0.2mm 时，残余应力均值较大，但方差较小，说明压下量为0.2mm 时残余应力波动较小，矫后稳定性高。在不同初始弧高对残余应力影响的统计分析中，不同弧高下的残余应力统计数值相接近，因此，不同初始弧高变化对残余应力影响较小。由表3 可知，不同压下量对矫后塑性应变影响较大，塑性应变的最小值、最大值、均值、方差、标准差随着压下量的增大而增大，而初始弧高的变化对塑性应变的影响较小。

4 结论

（1）通过对板束有限元矫直模型的仿真与实验结果的对比，表明仿真矫直后的板束轮廓变化趋势和实验矫直后板束的轮廓变化趋势基本吻合，仿真后的板束平直度为：0.137mm/m，实验后的板束平直度为：0.172mm/m，二者不平度仅相差2.03%，说明了有限元模型的准确性。

（2）在板束长度方向上取三条路径进行应力、应变分析，表明矫后板束的上表面路径和下表面路径的残余应力数值较大且波动剧烈，中部路径残余应力数值较小且波动平缓。矫后板束上表面路径、中部路径、下表面路径的塑性应变的分布规律和残余应力分布规律相似，即板束的上表面路径和下表面路径的塑性应变数值较大且波动剧烈，中部路径塑性应变数值较小且波动平缓。

（3）对板束的矫直效果进行影响因素分析，表明压下量对板束矫直效果影响最大，即当压下量为0.2mm时，板束矫后的残余应力数值较大，但波动平缓，板束矫后的塑性应变数值较小，波动平缓，板束在压下量为0.2mm时的矫后平直度最好；选取的不同初始弧高的板束在同一矫直工艺参数下的矫后残余应力数值大小和波动范围接近，各不同弧高对应的矫后塑性应变数值大小和波动范围也接近，表明所取板束不同初始弧高对板束矫后的残余应力和塑性应变影响较小。