车辆质心侧偏角容积卡尔曼滤波软测量方法

张 婧，张芝雨，季 晔

（1.许昌职业技术学院机电与汽车工程学院，河南 许昌 461000；2.洛阳理工学院机械工程学院，河南 洛阳 471023）

1 引言

近年来，随着汽车制造业的发展，汽车产业技术逐步壮大与成熟，汽车产品力日益提升，业内竞争也愈发激烈。伴随而来的是整个行业对于行业链中产品品质的精益求精，以及人们对于乘坐体验要求的日益提高。此外，汽车的智能制造与智能控制技术也得到了空前的关注于大力发展［1-2］。智能车集成了诸多的先进控制技术，具有更高的道路利用率与操纵稳定性，尤其是L3级别的智能车辆技术是当前的研究热点之一。在车辆控制技术应用中，准确可靠的环境感知信息与车辆自身行驶状态信息是决定车辆动力学控制性能好坏的关键一环［3-4］，因此，进行智能车行驶状态估计方面的研究具有非常重要的理论价值与实践意义。

卡尔曼滤波及其诸多的改进形式在车辆参数与车辆行驶状态估计的研究中得到了广泛的应用［5］，是一种普遍且有效的估计手段。文献［6］在考虑车辆模型的非线性特性基础上，结合自适应神经模糊推理方法与无迹卡尔曼滤波提出了一种车辆质心侧偏角估计方法，利用低成本传感器得到了准确的车辆状态估计量。文献［7］设计了一种车辆状态扩展卡尔曼滤波（Extended Kalman Filter，EKF）估计方法，并结合自适应辅助滤波的方式，通过误差迭代提高了估计精度。文献［8］考虑了非高斯噪声与轮胎的非线性，提出了一种将辅助粒子滤波与迭代扩展卡尔曼滤波相结合的估计方法。观察现有研究可知，在进行车辆行驶状态滤波估计中，通常将由惯导装置采集到的车辆横摆角速度或纵横向加速度作为测量方程的更新输入量［9-10］。然而，依赖单个装置或传感器测量所得的状态信息一旦出现故障或者受到外界未知干扰，容易对估计结果造成较大的偏差。四轮轮速耦合关系与车辆行驶状态息息相关，且轮速传感器价格相对较低，轮速信息相对较易获得，若将其应用到车辆状态滤波估计中，可以凭借测量信息的冗余度来提高整个估计系统的可靠性，因此具有较大的研究价值与空间。

针对车辆质心侧偏角软测量问题，提出了一种基于自适应容积卡尔曼滤波（Adaptive Cubature Kalman Filter，ACKF）的智能车质心侧偏角耦合估计方法。建立了三自由度车辆模型、轮胎模型、轮速耦合模型，并采用卡尔曼滤波进行车辆状态估计。结合车辆模型，设计了自适应渐消矩阵提高增益矩阵的调节能力，并将轮速耦合关系应用到ACKF的测量更新方程中，利用测量信息的冗余度来提高估计结果的精度与可靠性。

2 车辆动力学模型

2.1 三自由度车辆模型

为了实现车辆行驶状态估计方法的设计工作，需要定义与表征界定研究条件与范围下的车辆动态模型。车辆建模中所设定的建模条件与研究范围可以表示为：考虑车辆行驶水平平面内的动力学状态，研究车辆纵横向以及横摆方向的动力学方程，建立坐标系并将其表示为xoy，且将其原点放置于车辆质心。坐标系的x轴与y轴分别代表车辆运动的纵、横向。常规车辆的四个车轮的轮胎型号与安装方式、安装工艺通常来说是一致的，故这里设定车辆四个轮胎的特性相同。如图1所示，从而可建立车辆的三自由度动力学模型，且车辆动力学方程可以表示为：

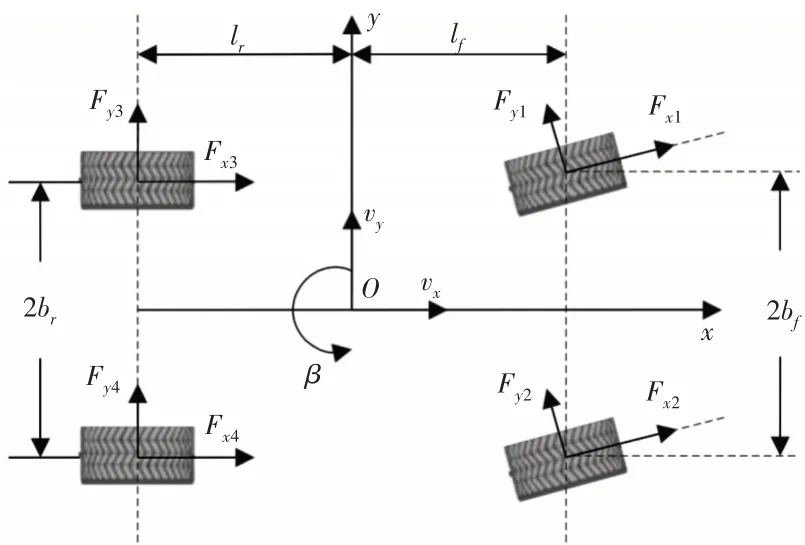
图1 三自由度车辆模型Fig.1 Vehicle Model with 3 Degree of Freedom

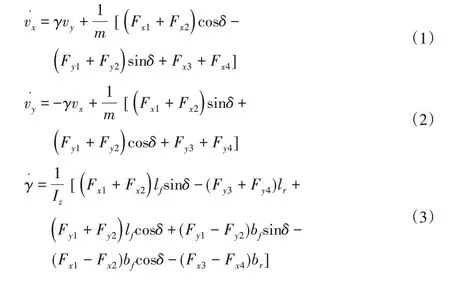
式中：vx—纵向车速；vy—侧向车速；γ—横摆角速度；m—汽车质量；Fxj和Fy（jj=1，2，3，4）—轮胎的纵向力和侧向力；δ—前轮转角；Iz—绕z轴的转动惯量；lf—质心距前轴的距离；lr—质心距后轴的距离；bf—前轮距的1/2；br—后轮距的1/2。

2.2 轮胎模型

魔术公式是目前公认且应用较为普遍的轮胎模型之一，对表征轮胎力具有较好效果。故这里采用成熟的基于魔术公式的轮胎模型对车辆的轮胎力进行计算，魔术公式可表示为：

式中：Y（X）—纵向轮胎力或侧向轮胎力；

X—滑移率s或轮胎侧偏角α；

B—刚度因子；

C—曲线形状因子；

D—峰值因子；

E—曲线曲率因子；

sh和sv—水平偏移和垂直偏移。

轮胎模型参数B、C、D、E都与轮胎的垂直载荷相关，各轮胎的垂直载荷为：

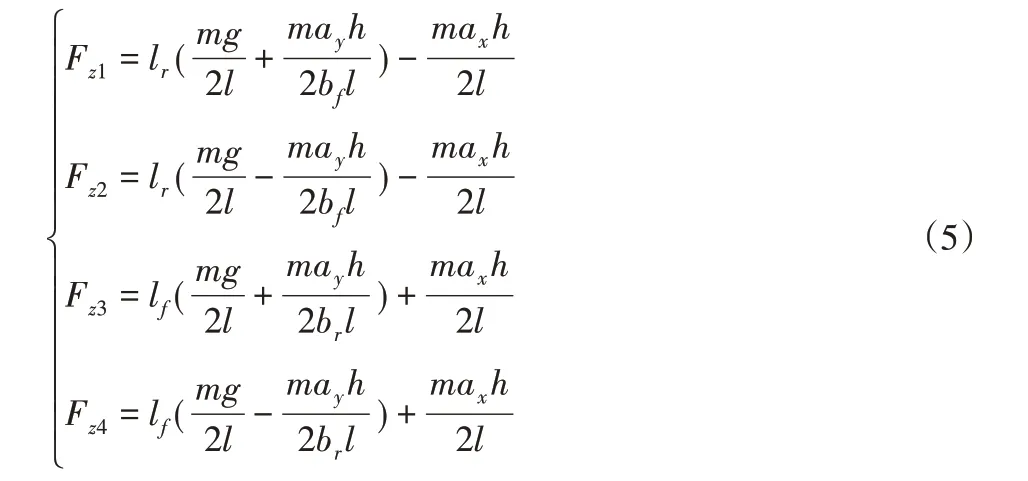
式中：Fz1、Fz2、Fz3、Fz4—对应轮胎的垂直载荷；h—质心高度；g—重力加速度。各轮胎侧偏角为：

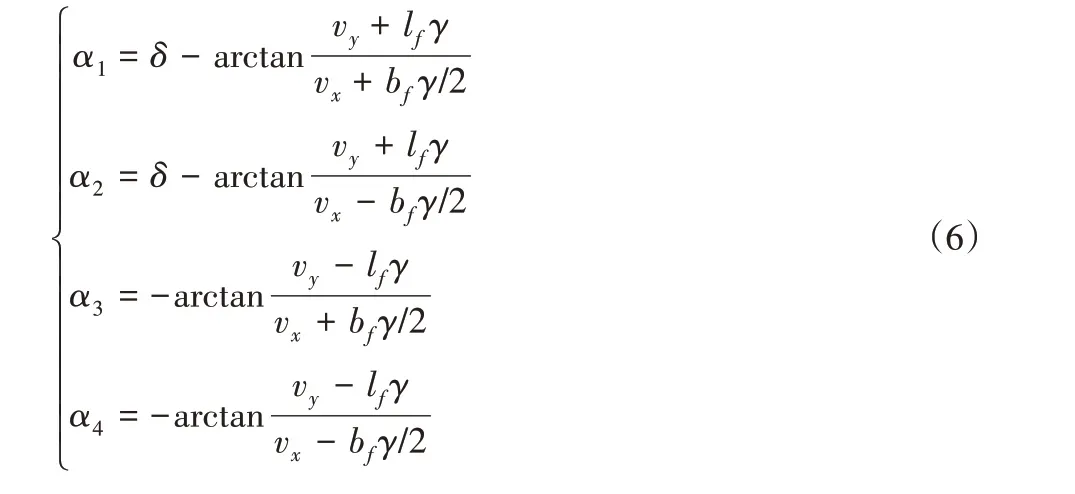
3 车辆质心侧偏角估计方法设计

3.1 基于ACKF的车辆状态估计方法

针对式（1）～式（3）中的车辆模型，可将其表示成如下的离散状态空间方程：

式中：xk—离散系统的状态空间向量；yk+1—离散系统的测量向量；（f·）—离散系统的状态转移函数；h（·）—离散系统的测量函数；wk和vk—互不相关的高斯白噪声。则式（1）～式（3）离散化结果可表示为：

式中：T—滤波迭代步长。

容积卡尔曼滤波（CKF）相比常见的扩展卡尔曼滤波降低了滤波的发散现象，其计算量仅仅与待估计系统的状态维数成正比，故相比粒子滤波其计算量又大大减小，因此近年来在诸多领域得到了广泛的应用。由于车辆行驶状况较为复杂，在非线性干扰或者一些不确定性因素作用下，常规CKF算法的估计精度以及估计稳定性很有可能受到影响。利用Sage滤波开窗法，结合多重次优渐消因子，设计ACKF算法用于车辆质心侧偏角估计，有助于提升估计效果。依据式（7）中的车辆非线性状态空间方程，ACKF算法迭代步骤可表示为：

（1）选取初值点。

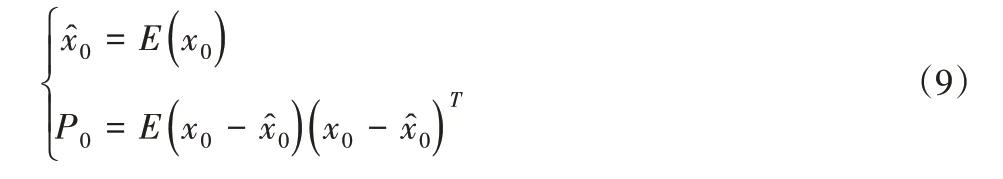
式中：x0—初始状态向量；P0—误差协方差阵。

（2）计算容积点。

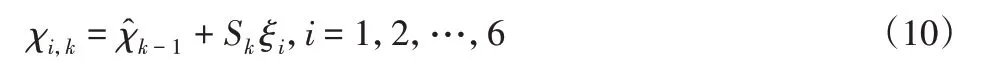
式中：i—容积点编号；Sk—Pk|k通过Cholesky分解所得且有Pk|k=—容积点，即容积点集可表示为：

（3）时间更新。

容积点传播，根据状态转移方程得到容积点：

状态一步预测：

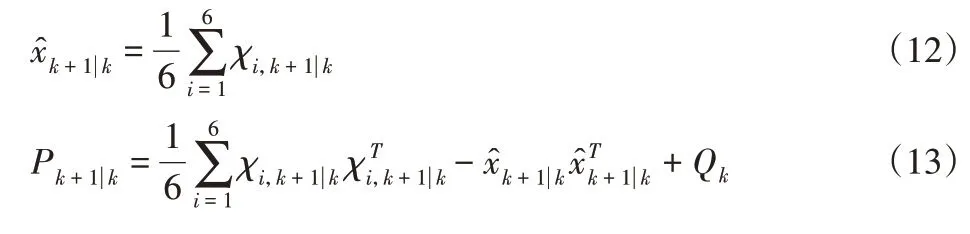
式中：Qk—wk的协方差阵。

（4）测量更新。

对Pk+1|k进行Cholesky分解可得：

计算容积点：

容积点传播：

测量预测值为：

测量预测协方差矩阵和互协方差矩阵分别为：

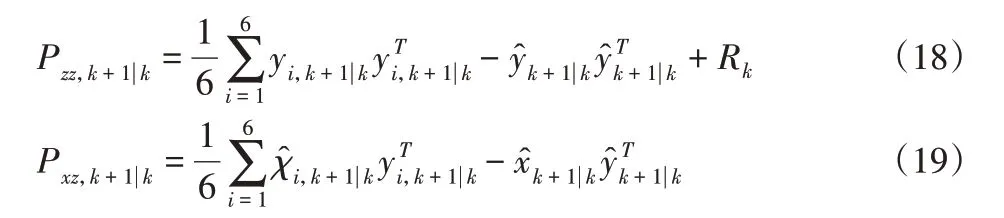
式中：Rk—vk的协方差阵。

预测误差εk+1|k可由实际测量值与预测测量值作差得到：

式中：yk+1—k+1时刻的实际测量值；

3.2 含自适应渐消矩阵的滤波增益设计

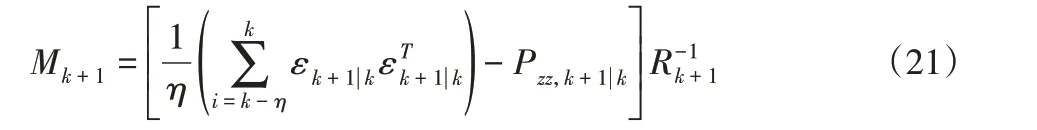
式中：η—滑动窗口宽，这里选取η=220。

观察式（21）可知，渐消矩阵Mk+1能够随着测量噪声的变化而自适应调整。然而，随着迭代误差的累积，渐消矩阵Mk+1的对角线元素有可能小于1，因此需要对渐消矩阵Mk+1进行进一步的修正，将其设计为：

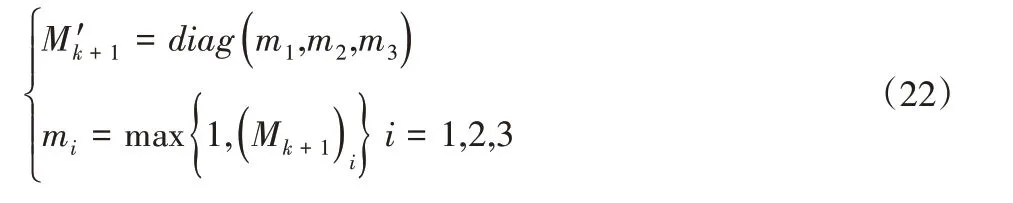
式中：(Mk+1)i—修正前渐消矩阵Mk+1的第i个主对角元素。

从而，含自适应渐消矩阵的滤波增益可设计为：

观察式（23）可知，当测量噪声异常变化时，修正渐消矩阵对应项Mk′+1将同样增加，则自适应滤波增益将会相应减小，从而削弱测量噪声异常对估计结果的影响。在完成自适应滤波增益的设计之后，继续进行测量更新的余下迭代步骤，即为车辆状态估计：

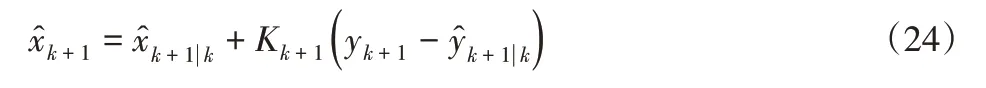
以及计算车辆状态误差协方差矩阵：

3.3 基于多信息融合的质心侧偏角估计

根据式（9）中的车辆非线性方程，利用上节中的ACKF算法可进行车辆状态估计，其中状态量为xk+1=[vx，k+1vy，k+1γk+1]T。在现有文献中，常选取车辆侧向加速度作为实际测量更新的输入量。纵向和横向车辆加速度可以表示为：

式中：ax和ay—车辆的纵向和横向加速度。

在轮胎模型中，侧向加速度也与轮胎力的计算结果息息相关，一旦车辆的惯导装置出现了难以预知的偏差，很容易造成误差自我循环以及误差累积，从而使得滤波估计结果逐渐偏离实际值。四个车轮的轮速之间满足如下关系：

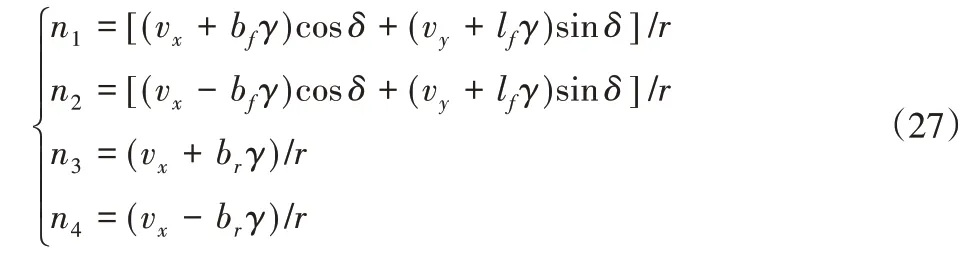
为了避免这一问题，将式（27）中的轮速耦合关系应用到测量更新迭代中，结合纵横向加速度的测量信息，将滤波器的测量状态量设定为yk=[ax，k ay，k n1，k n2，k n3，k n4，k]T，从而可充分利用测量信息的冗余度，基于多信息融合的方式提高估计结果的可靠性。利用上节的ACKF 算法，可得车辆行驶状态估计结果，从而车辆质心侧偏角估计值为：

4 仿真验证

为了验证这里所设计的基于ACKF的智能车质心侧偏角耦合估计方法的估计性能，基于CarSim和Simulink软件搭建了联合仿真模型并进行了仿真试验，然后将EKF的仿真估计结果与ACKF的仿真估计结果进行对比分析。试验中仿真参数，如表1所示。

表1 车辆参数Tab.1 Vehicle Parameters

4.1 双移线工况

双移线仿真工况，如图2所示。仿真工况具体设定为：车速25m/s，道路附着系数1.0，滤波迭代步长0.001s，状态初值x0=[ 25 0 0]T，误差协方差矩阵P=eye( 3 )×103，测量噪声协方差矩阵Q=eye( 6 )×103。仿真结果，如图3所示。其中，纵向车速、侧向车速、横摆角速度和质心侧偏角，如图3（a）～图3（d）所示。在整体估计趋势上，EKF和ACKF都能对车辆行驶状态进行很好地跟踪。但根据图3（a）、图3（b）、图3（d）以及图3（c）的局部放大图可知，在车辆行驶状态的峰值处，ACKF的估计精度明显高于EKF。

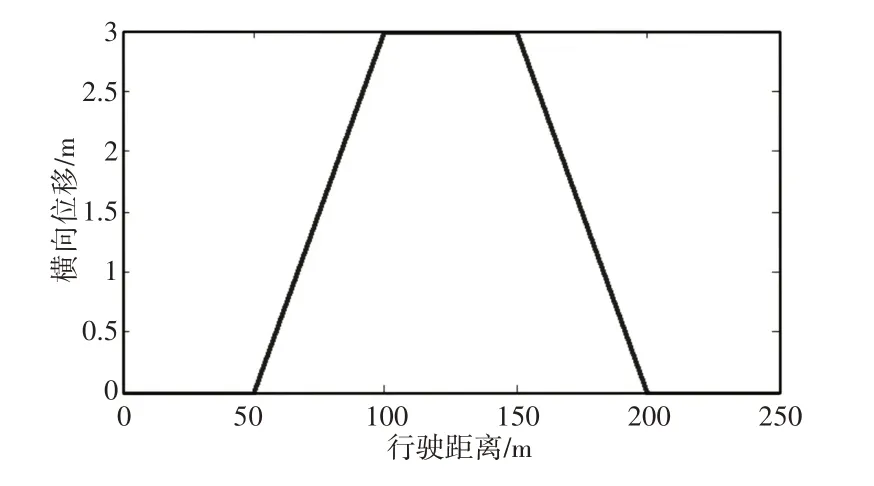
图2 双移线工况Fig.2 Double Lane Changes Manoeuvre

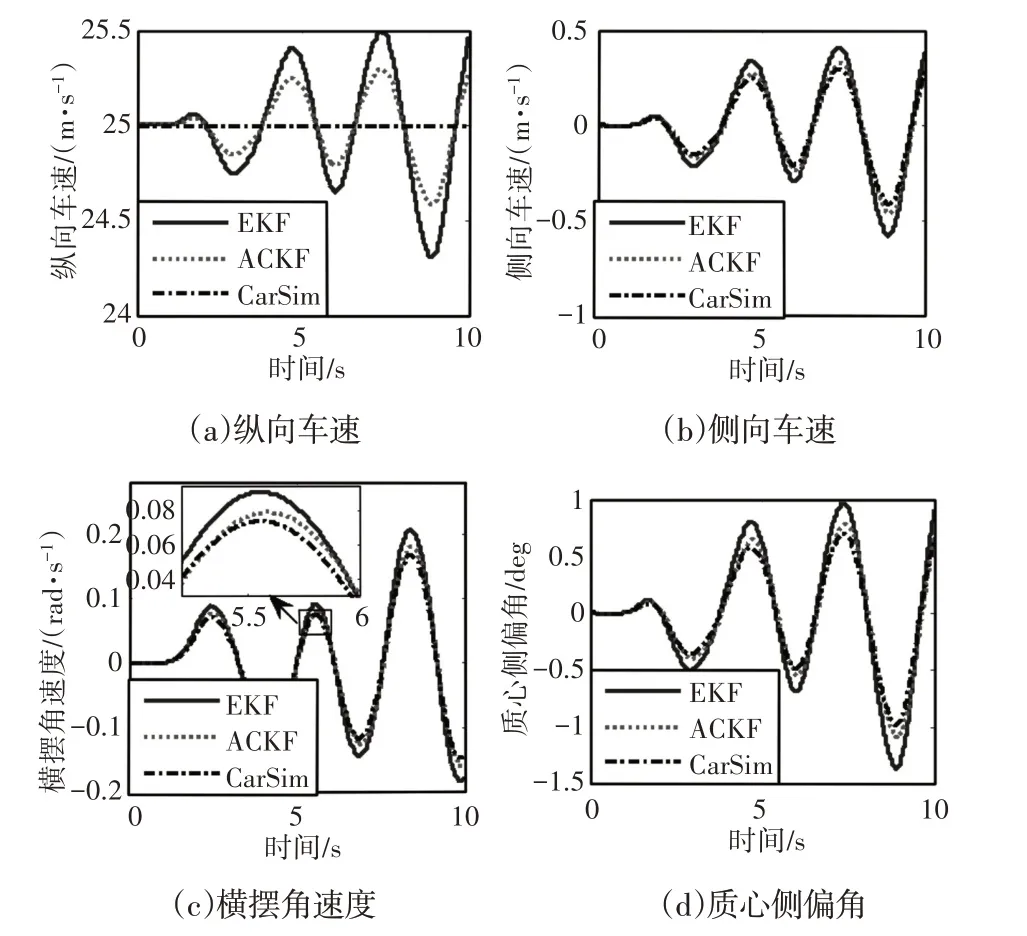
图3 双移线工况估计效果对比Fig.3 Comparison of Estimation Effects in DLC Manoeuvre

为进一步定量化地体现ACKF对估计精度的提升效果，采用估计结果的误差平均值（Average Error，AE）和误差均方根值（Root Mean Square Error，RMSE）来表征提出方法的估计效果（下同），计算公式为：

式中：n—采样常数；

xi—第i个采样时刻的车辆实际状态与估计状态。

双移线工况下估计结果的量化对比分析，如表2所示。由表2可知，EKF的AE和RMSE都小于ACKF，说明ACKF提高了整体估计结果的精度和稳定性。按照AE来评价估计精度提升效果，计算可得，相比EKF来说，ACKF对于纵向车速、侧向车速、横摆角速度和质心侧偏角的估计精度分别提升了0.20%，17.60%，4.23%，17.28%，取其平均值为整体估计精度提升比，即9.83%。

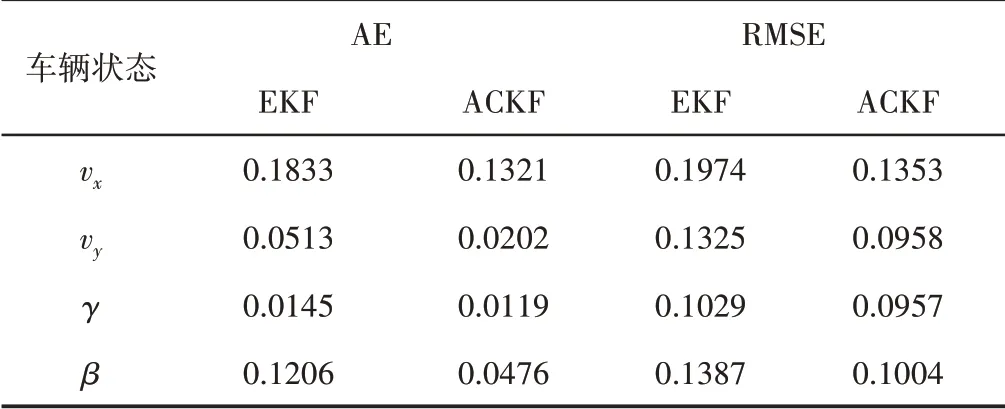
表2 双移线工况估计结果定量分析Tab.2 Quantitative Analysis of Estimation Results in Double Lane Change Manoeuvre

4.2 J-turn工况

为了进一步验证所提出的估计方法在复杂工况下的估计效果，进行了变车速低附着急转向情况下的仿真试验。J-turn工况仿真如图4所示。仿真工况具体设定为：道路附着系数0.5，滤波迭代步长0.001s，状态初值x0=[ 10 0 0]T，误差协方差矩阵P=eye( 3 )×103，测量噪声协方差矩阵Q=eye（6）×103。仿真结果，如图4所示。其中，纵向车速、侧向车速、横摆角速度和质心侧偏角，如图4（a）～图4（d）所示。通过图4（a）中局部放大图和图4（c）可知，ACKF 的纵向车速和横摆角速度估计效果优于EKF。由图4（b）和图4（d）可知，相比EKF，ACKF对侧向车速和质心侧偏角的估计精度提升较为明显。相比CarSim输出的实际车辆状态，ACKF的估计结果存在一些滞后，这主要是由于ACKF计算量更大导致的。而且相比侧向车速和质心侧偏角的量级来说，这种滞后导致的估计误差是非常小且在可容许范围内的。图4中的仿真结果表明：在车辆行驶状态变化剧烈、行驶工况较为严峻的情况下，所提出的基于ACKF的耦合估计方法仍能保持精确的估计性能，验证了所提出方法的抗干扰性与可靠性。按照式（32）、式（33）计算J-turn工况下的AE值和RMSE值，所得结果，如表3所示。可知J-turn工况下ACKF的AE值和RMSE值都小于EKF。相比EKF来说，ACKF对于纵向车速、侧向车速、横摆角速度和质心侧偏角的估计精度分别提升了0.47%，12.52%，3.06%，12.44%，整体估计精度提高了7.12%。从而，所提出估计方法的估计效果得到了验证。

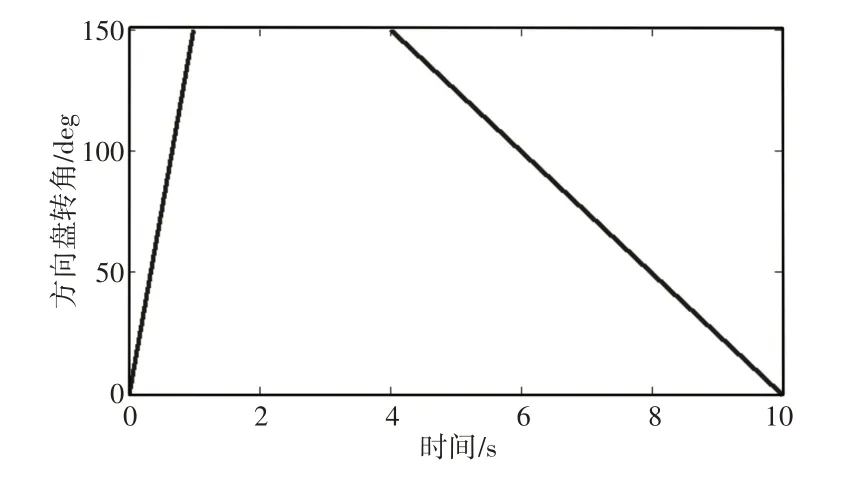
图4 J-turn工况Fig.4 J-turn Manoeuvre

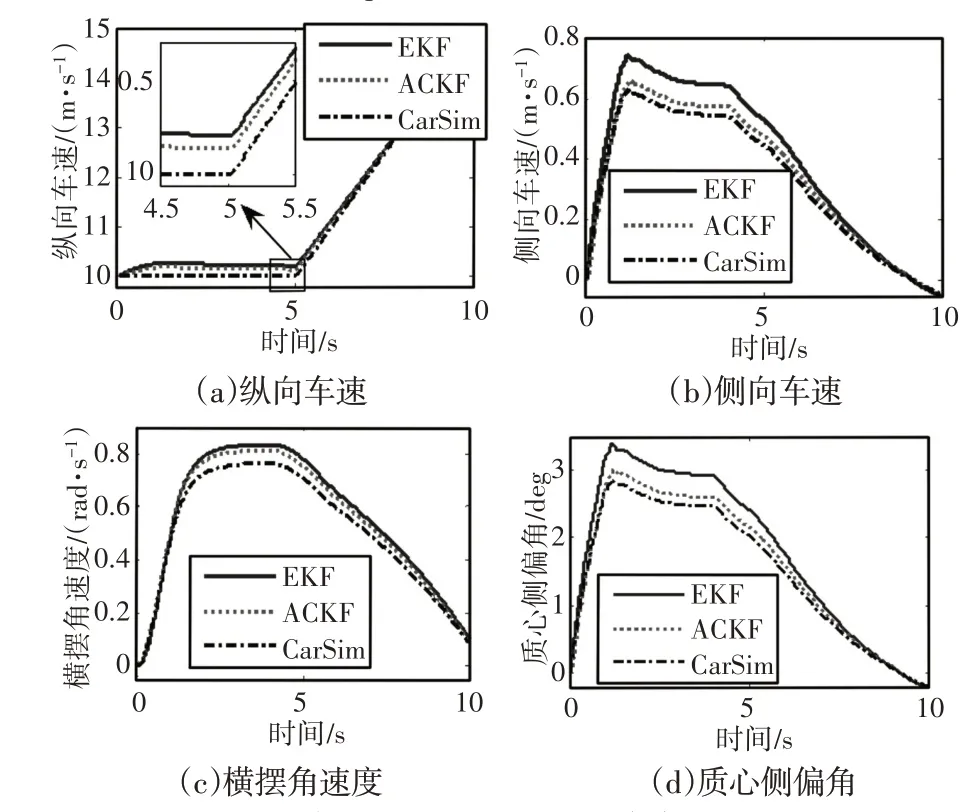
图5 J-turn工况估计效果对比Fig.5 Comparison of Estimation Effects in J-turn Manoeuvre

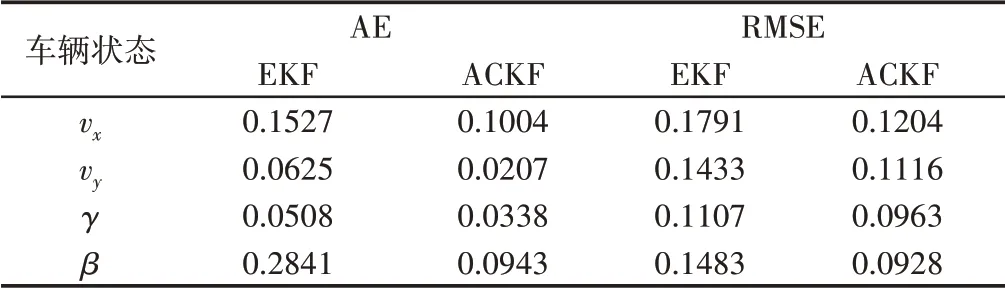
表3 J-turn工况估计结果定量分析Tab.3 Quantitative Analysis of Estimation Results in J-turn Manoeuvre

5 结论

（1）针对车辆质心侧偏角估计问题，建立了车辆三自由度动力学模型、轮胎模型和轮速耦合模型，并基于ACKF设计了车辆质心侧偏角耦合估计方法。（2）设计了含自适应渐消矩阵滤波增益的ACKF，来提高滤波过程中的噪声自适应性，并利将轮速耦合关系应用到滤波测量更新中，提高了估计结果的可靠性。进行了基于CarSim 和Simulink 联合仿真模型的仿真试验，并将EKF估计结果与ACKF进行对比分析。（3）结果表明：相比EKF，所提出的估计方法能够实现更为精确车辆状态估计，具有更好的实时性与可靠性，整体估计精度分别提升了9.83%和7.12%。