深海能源土抗剪强度的理论研究

2022-05-19戚承志朱守东王晓娇

长江科学院院报 2022年5期

于航，戚承志，朱守东，赵发,王晓娇

(北京建筑大学北京未来城市高精尖中心与城市基础设施建设北京市国际合作基地，北京 100044)

1 研究背景

海洋土与陆地土有很大的区别，一是承受着更大的孔隙水压力，二是形成了与陆地土差别很大的海洋土胶结物质，简称水合物。水合物是21世纪的主要清洁能源。含有水合物的海洋沉积物也称为深海能源土。在全球能源紧张的坏境下，对水合物的开采引起了重视，因此，为了保证开采的安全以及避免海底灾害的发生，正确认识水合物沉积物的力学性质是十分必要的。为此国内外不少学者针对海洋土力学特性展开了研究。

Cuccovillo等[1]对能源土进行了电子显微扫描，发现水合物广泛地存在颗粒之间。试验发现，深海能源土的力学性质受水合物的分布模式、含量等影响，水合物的含量和赋存状态对于土的力学性质的影响较为明显。赋存状态根据饱和度的增大分为3种：填充模式、持力体模式、胶结模式[2-4]，如图1所示。其中胶结模式对力学性质的影响最为明显，其主要原因是水合物的胶结作用能将周围的土颗粒胶结在一起形成一个整体骨架承载。

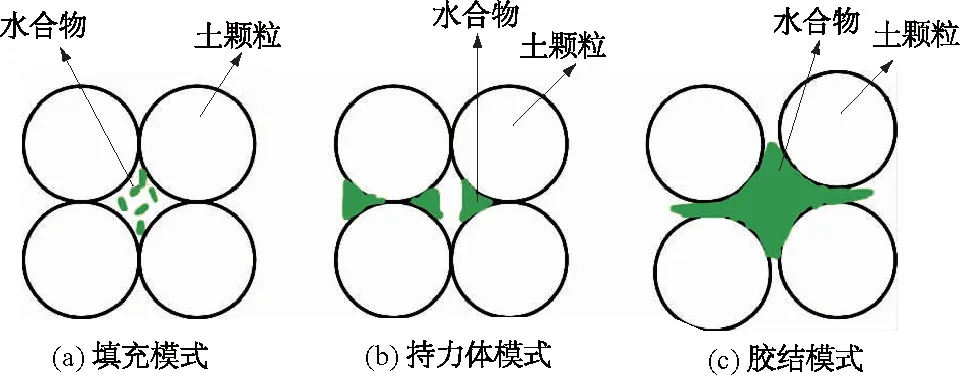
图1 水合物的赋存模式[2-4]Fig.1 Occurrence mode of hydrate[2-4]

对于能源土力学性质的研究，国内外学者已进行了大量的试验并获得了比较可靠的规律。Hyodo等[5]进行了能源土的三轴试验，发现随着水合物饱和度的增加，能源土抗剪强度增加；但水合物饱和度存在临界值，未达到临界值时强度变化不明显，达到临界值之后强度变化明显，说明水合物不同赋存模式对强度有较大影响。

蒋明镜等[6-7]开展了颗粒间水合物胶结宽度和厚度对能源土力学性质的影响，发现胶结宽度和厚度不同时，水合物力学性质也不相同，胶结宽度和厚度的不同总的来说可以归结为饱和度的不同。杨周洁等[8]利用自主研发的含水合物沉积物三轴试验机得到了不同围压和水合物饱和度对水合物沉积物强度和刚度的影响，说明水合物的含量对强度和刚度的影响是比较明显的。颜荣涛等[9]考虑水合物作为持力体以及胶结物提出了天然水合物沉积物的强度模型，能够反映不同赋存模式、不同含量、不同围压下沉积物的强度特性，但模型中的公式存在缺陷。

从上述学者展开的研究工作发现，颗粒间水合物饱和度对力学性质的影响是比较明显的。但目前大部分是通过试验得出的规律，对于理论的研究仍然存在缺陷。另外，水合物分解也会对力学性质产生较大影响。水合物的赋存稳定性对温度和压力条件十分敏感，极容易发生分解。张旭辉等[10]对以蒙古砂为骨架的水合物沉积物在分解前和分解后进行不排水剪切试验并得到应力-应变曲线，发现水合物分解后的强度远低于分解前的强度，约为分解前的1/7。

水合物分解造成沉积物强度降低有2个原因：一是水合物分解产生水和天然气，固态物质转变成液态，会降低沉积物的抗剪强度；二是沉积物层一般为淤泥质土层，透水性比较差，并且认为水合物分解产生甲烷气体的速率快于孔压消散的速率，此时可以将水合物分解的过程看成不排水过程，在这种条件下水合物分解会导致孔隙压力增大形成超压，有效应力减小，使沉积物的强度大大衰减[11]。当土体的抗剪强度达到土体破坏的临界状态时，便会发生海底滑坡。

由于沉积层中水合物分解产生的超孔隙压力难以通过实验测得，所以不少学者开展了超孔隙压力的理论和模拟分析。Xu等[12]研究了不同渗透性的海洋沉积物中水合物分解产生的超孔隙压力，水合物产生的甲烷气体溶解使周围土层的甲烷溶度降低使水合物继续发生分解，导致土体发生破坏。但该模型存在无法确定的参数，适用性有限。Grozic等[13]通过引入热力学的概念计算水合物分解的超孔隙压力，但没有给出具体的推导过程，并且存在比较难取值的土体参数，且未考虑甲烷气体在高压条件下在海水中的溶解。洪隽天等[14]通过FLAC3D模拟了水合物分解对边坡稳定的影响，并给出水合物分解后的孔隙压力表达式，将模拟结果与理论解进行了对比，能够较好地分析水合物分解对海底边坡稳定的影响，但同样未考虑甲烷气体的溶解。

综上，水合物对能源土强度影响的理论分析需要进一步研究。本文从2个角度分析水合物强度增大的原因。首先，根据图1，当水合物赋存模式变为持力体模式后，水合物的存在会增大颗粒间的接触面积，且随着水合物饱和度的增加，接触面积越大，这将增大颗粒之间的摩擦强度；其次，高孔压和水合物胶结作用会增大颗粒之间的黏聚力。根据上述分析，本文基于路德春等[15]对有效应力的分析，修正考虑水合物的有效应力表达式，同时提出考虑水合物种类和赋存模式的黏聚力表达式，从理论上分析抗剪强度与水合物饱和度之间的关系。另外修正了考虑甲烷气体溶解的水合物分解的孔压计算模型，从理论上分析了水合物分解使能源土抗剪强度降低的机理。本研究可为试验规律提供理论依据，为海洋岩土工程的开发和建设提供理论参考。

2 水合物的存在对抗剪强度影响的理论分析

2.1 水合物的存在对有效应力的影响

土体单元所受总应力以及土颗粒和孔隙水所承担的应力如图2所示，此处认为任意单元的孔隙率和密度是相同的，颗粒排列杂乱，表现为各向同性。并且假设将水合物作为土骨架的一部分，认为二者作为两种连续介质材料具有相同的应变。

图2 截面受力分析示意图Fig.2 Analysis of forces acting on cross-section

图2中σ为土体所受外荷载，σs为土颗粒承担的外荷载。孔隙水压力为u，总的横截面积为A,孔隙水的截面积为Aw，土颗粒的截面积为As，且A=As+Aw。由于水合物的存在增大了颗粒之间的接触面积，所以As可认为是水合物胶结面积的水平投影面积Ac，且随着水合物饱和度的增大(变为持力体模式后)，Ac增大。在a-a截面根据法线方向的平衡方程为

σA=(σs+u)Ac+uAw。

(1)

两边同时除以A可得

(2)

从上述推导结果可以看出，在推导的有效应力表达式中，随着水合物的饱和度增大，胶结面积比δ增大，有效应力线性增大。

2.2 水合物的存在对黏聚力的影响

首先，水合物本身的胶结作用会使土颗粒之间产生黏聚力，并且随着水合物饱和度的增加，黏聚力越大。目前多采用线性拟合表示水合物饱和度和黏聚力之间的关系[16]。根据张旭辉等[17]对不同水合物沉积物力学性质的试验研究中提供的黏聚力参数，得到不同种类的水合物对黏聚力影响是不同的。因此本文提出黏聚力与饱和度的关系式如式(3)所示，并绘出不同种类水合物沉积物黏聚力随水合物饱和度的关系，如图3所示。

图3 不同水合物沉积物的黏聚力与饱和度的关系Fig.3 Variation of cohesion of different hydrate sediments with saturation

c′t=c′+kS′h。

(3)

式中：c′t为含水合物土颗粒之间的有效黏聚力；c′为不含水合物的有效黏聚力；k为比例系数，反映不同水合物材料的影响；S′h为水合物饱和度。

另外，高水压对固体颗粒会产生压缩作用。水合物胶结作用使颗粒粘结在一起，增大了土颗粒之间的接触面积，土颗粒在高孔隙水压力的作用下，颗粒之间的接触应力变得更大，黏聚力增大，增大的黏聚力可以表示为uδ，如图4所示。即使孔隙压力足够大使得有效应力为0，该部分对抗剪强度的影响也是比较大的。

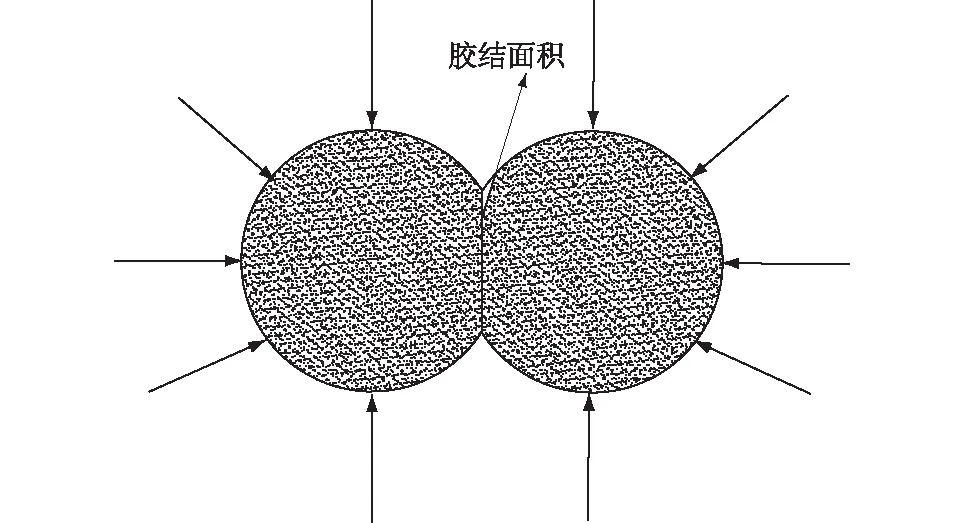
图4 高孔压对土颗粒黏聚力影响示意图Fig.4 Schematic diagram of the influence of high pore pressure on soil particle’s cohesion

土的抗剪强度的摩尔-库伦准则表达式为

τf=σ′tanφ′+c′ 。

(4)

式中：τf表示抗剪强度；c′为有效黏聚力；φ′为有效内摩擦角。

将式(2)和式(3)以及uδ代入式(4)得

τf=(σstanφ′+u)δ+kS′h+c′ 。

(5)

为了能比较直观地分析出抗剪强度与水合物饱和度之间的关系，需进一步分析胶结面积比δ与内摩擦角φ′与水合物饱和度之间的关系。刘乐乐等[18]发现水合物的饱和度对内摩擦角没有明显的影响，因此内摩擦角为定值。由于缺少试验规律反映水合物饱和度与胶结面积比δ之间的关系，因此本文通过杨期君等[19]制备水合物离散元试样时针对不同水合物饱和度设置的水合物颗粒数目来假设水合物饱和度和胶结面积比之间的关系。该模拟共设置了3种不同水合物饱和度的试样，分别为10%、20%、30%。3种饱和度对应的水合物的颗粒数分别为4 473、8 947、1 3421，颗粒数目是呈线性增加。由于水合物颗粒的直径一样，因此胶结面积也是呈线性增加。故本文同样假设胶结面积比与水合物饱和度之间是线性关系。

2.3 试验验证

为了证明该公式的合理性，引入颜荣涛等[20]水合物对砂土强度影响的三轴剪切试验。该试验采用非饱和成样法(称为第1种方法)和饱和试样气体扩散制样法(称为第2种方法)两种方法制备水合物砂土试样，以研究不同赋存模式下水合物对砂土强度的影响。本文引用两种方法制得试样得到的抗剪强度与水合物饱和度的试验数据与理论值进行了对比。

图5 抗剪强度与水合物饱和度关系曲线[20]Fig.5 Relation of shear strength versus hydrate saturation[20]

图6 颜荣涛等[9]强度模型模拟结果Fig.6 Simulation results of Yan Rongtao’s strength model[9]

3 水合物分解对抗剪强度的影响

由前文分析可知，水合物分解对沉积物的强度的影响是十分明显的，尤其是水合物分解产生超孔隙压力会影响海底边坡的稳定性，且深海区域随着压力增加，超孔隙压力增大得更快。所以通过理论来计算水合物分解产生的超孔隙压力值对水合物的开采以及避免海底灾害的发生有一定的参考意义。

3.1 孔隙压力计算

Duan等[21]研究了不同热力学温度T下甲烷气体在高压情况下的溶解度，溶解平衡曲线如图7所示。随着孔压的增大及温度的降低，甲烷气体的溶解度也增大，甲烷气体溶解会在一定程度上缓解孔隙压力的增长。为了更直接地与工程和实际相结合，甲烷气体的溶解是不能忽略的。

图7 孔隙压力与甲烷气体溶解度的关系Fig.7 Relationship between pore pressure and methane solubility

水合物分解引起的体积变化如图8所示，图中W、S、H分别表示为水、土颗粒和水合物的体积；W1、G表示为分解后产生的水和气体的体积；H1表示未分解的水合物体积。体积变化可以表示为

图8 水合物分解引起的体积变化Fig.8 Volume change caused by hydrate decomposition

ΔV=Vg0+VwH-V′g-V′H。

(6)

式中：Vg0表示为常温常压下水合物分解产生的甲烷气体的体积；VwH为水合物分解产生的水的体积；V′g为产生的甲烷溶于水的体积；V′H为分解的水合物的体积。

在常温常压下，1 m3的水合物分解将产生164.6 m3的甲烷气体和0.87 m3的自由水[22]。所以VwH=0.87V′H，Vg0=164.6V′H。

对于在海洋沉积物层，温压条件与常温常压条件并不一致，所以水合物分解产生的甲烷气体的体积与常温常压条件下并不相同，根据理想气体的状态方程uV=mRT(其中V为气体体积，m为气体物质的量，R为摩尔气体常数，T为海底沉积物层的热力学温度)，可以得到实际温压条件下水合物分解产生的甲烷体积(在常温常压下初始孔压u0=101.325 kPa，初始温度T0=298.15 K)。

理想气体状态方程为

(7)

式中：u0为初始海底沉积物层的孔压；u为水合物分解后沉积物层的孔压；Vg为实际温压条件下水合物分解产生的甲烷体积。

所以Vg可表示为

(8)

根据气体溶解度的定义可知，溶解于海水的甲烷气体的体积为(这里假定认为未分解前孔隙中不存在气体)

V′g=Vws=(Vw0+0.87V′H)s。

(9)

式中：s为在实际温压条件下甲烷在海水中的溶解度；Vw为孔隙中自由水的体积；Vw0为初始孔隙中海水的体积。

根据自由水的饱和度以及孔隙体积的概念可以得到

Vw=nVSr+0.87V′H。

(10)

式中：Sr为自由水的饱和度；V为沉积物的体积；n为孔隙率。

将式(10)代入式(9)可以得到常温常压下水合物分解产生甲烷气体的体积为

V′g=(nVSr+0.87V′H)s。

(11)

将式(8)和式(11)代入式(6)得

(12)

水合物分解使得有效应力减小，体积膨胀，这与卸载回弹过程类似，土骨架变形满足胡克定律，即

(13)

式中：Δσ1、Δσ2、Δσ3表示3个方向应力的变化值；K′为卸载过程中土骨架的平均体积模量。

由于土体处于侧限条件，假设上覆土体和海水的深度不变，因此竖向总应力不变。水平向有效应力改变量可以表示为竖向有效应力改变量以及泊松比的函数，即：

(14)

(15)

式中：V为总体积；ν为泊松比。

土骨架的压缩模量ES可以表示为

(16)

所以结合式(12)和式(15)可以得到只含有当前孔压u的一元二次函数，即

(17)

其中：

式中：η表示水合物分解程度；VV表示沉积物孔隙的体积。

求解可得

u=0.5{u0-0.13λES-(nSr+0.87λ)sES+

(18)

3.2 公式验证

目前对于水合物分解产生的超孔隙压力的研究还比较少，并且对于沉积物的试样采集也不太容易，很难通过试验来论证该结果的正确性。所以本文根据洪隽天等[14]利用FLAC3D对水合物分解过程模拟采用的土体力学参数(模型参数见表1)进行计算，将计算结果与模拟结果,以及其提出的孔压计算方法得到的理论解进行对比。

表1 模型单元参数Table 1 Model unit parameters

该模拟在计算孔压升高值时没有考虑甲烷气体的溶解结果,从而得到的超净孔压模拟值为261 kPa，其理论解为263 kPa。由于本文考虑甲烷气体的溶解，计算的结果为253 kPa，相比于模拟结果和理论结果会减小，且随着甲烷溶解度的增大，孔隙压力增大的程度更小。综上，本文修正的孔压模型更接近实际情况，更能描述孔隙压力增长规律，因此公式具有一定的参考意义。

3.3 水合物分解引起的抗剪强度的变化

根据式(5)可以看出，水合物分解使得饱和度减小导致胶结作用产生的黏聚力kS′h减小。根据式(3)有效应力可以写为σ′=σ-u，随着水合物的分解会产生更大的孔压即u增大，所以有效应力减小。但对于uδ这一项，尽管孔压增大,但水合物的分解使得胶结面积比减小，随着水合物分解孔压增大到一定程度，有效应力为0，颗粒之间也不再存在胶结作用，颗粒不再接触。因此，uδ这一项的影响会越来越弱，uδ随着水合物的分解可以忽略不计。另外，水合物分解也会使孔隙增大，含水量增大等从而使内摩擦角减小。所以综合上述分析，沉积物的抗剪强度随着水合物的分解减小，这样分解的水合物会形成一个滑动面，上部沉积物在重力作用下会发生滑坡，诱发海底灾害的发生。