基于多模态分类模型的芦山地震滑坡易发性评价

2022-05-19李齐荣苗则朗蒲明辉

长江科学院院报 2022年5期

李齐荣，苗则朗，陈帅，李珂，蒲明辉

(1.中南大学地球科学与信息物理学院，长沙 410083；2.中南大学地灾感知认知预知实验室，长沙 410083；3.长江三峡技术经济发展有限公司，北京 100038)

1 研究背景

我国地处环太平洋地震带和欧亚地震带之间，是世界上受地震影响严重的国家之一[1]。滑坡是地震的主要次生灾害，具有危害性强、分布范围大、发生频率高等特点。滑坡灾害每年都会造成大量的人员伤亡和财产损失，是我国主要自然灾害之一，特别是在西南地区的龙门山构造带上，如2013年4月20日的芦山Ms7.0级地震触发了22 528处滑坡，截止4月24日14时30分共造成约193人遇难[2-3]。此外，随着灾区灾后恢复重建和经济社会发展的有序推进，滑坡灾害的不确定性带来的潜在风险制约了灾区发展与规划。因此，科学准确地评价地震滑坡易发性对防灾减灾和规划重建具有重要意义。

滑坡易发性评价是降低滑坡风险影响的常用工具，能有效预测区域内滑坡发生的可能性。目前，国内外学者在滑坡易发性评价方面开展了大量研究，典型方法可分为定性和定量方法[4]。定性评价主要基于专家对滑坡的认知及实践经验，其评价结果精度不稳定而较少使用。随着对地观测技术和计算机技术的快速发展，定量评价方法被广泛应用于滑坡易发性评价。定量评价方法主要包括人工神经网络法、支持向量机法、随机森林法、逻辑回归法、频率比法等[5]。国内外学者为提升定量评价方法的评价精度开展了大量研究，如：滑坡影响因子选择[6-7]、评价模型参数优化[8-9]、不同模型之间组合优化[10-12]、区域划分[4,13]等。滑坡受多种影响因子相互作用的影响，而以往的研究大多只是简单地串联起影响因子，未考虑数据模态对评价精度的影响。与滑坡相关的数据模态主要有地震、地质、地形、水文等，不同模态的数据对滑坡发育的影响不同，可为滑坡易发性评价提供互补信息。在此基础上，本文提出一种新的滑坡易发性评价方法，即根据滑坡影响因子的固有属性将滑坡影响因子分为不同类型的模态数据，然后利用非线性图融合方法将不同的模态数据融合成统一的相似度图，再利用常用的分类算法对滑坡敏感性进行评价。

本文以芦山地震为例，根据前人的研究经验[14]并结合研究区地质环境以及数据可获取性，选取15个滑坡影响因子,包括地震峰值加速度(PGA)、距断层距离、地震烈度、岩性、高程、坡度、坡向、曲率、地貌类型、土地利用类型、土壤类型、距道路距离、距河流距离、地形湿度指数(TWI)和降雨量;然后采用本文提出的多模态分类(Multi-modal Classification, MMC)方法评价研究区地震滑坡易发性。

2 研究区概况和数据来源

2.1 研究区概况

芦山地震是继汶川地震后龙门山断裂带上又一次强烈地震，是由龙门山断裂带南段的逆冲运动造成的[15]。本文参考以往研究成果[16]，选定了一个椭圆区域作为研究区，其坐标范围为102°22′E—103°19′E，29°50′N—30°40′N，总面积约为5 396 km2。该区域位于四川省西南部，处于四川盆地与青藏高原之间的过渡地带，地形地貌复杂，地势整体呈西高东低，海拔范围539～4 850 m。根据芦山地震震后解译的滑坡编目，此次芦山地震共触发2万余处滑坡，滑坡总面积约19 km2，滑坡类型主要是深层滑坡、岩质崩塌、碎屑流等，其中多数为小型的岩质崩塌、土质滑坡与岩质滑动[17]。研究区地理位置及主要滑坡点分布如图1所示。

图1 研究区地理位置及滑坡点分布Fig.1 Location of Lushan earthquake and distribution of landslide points

2.2 数据来源

本研究采用的基础数据包括：①分辨率为30 m的数字高程模型(DEM)；②1∶500 000地质图；③中国区域地面气象要素驱动数据集(1979—2018年)中的2013年全国降雨数据[18-19]；④地震峰值加速度；⑤道路、河流和地表覆盖数据；⑥地震烈度；⑦土壤和地貌类型；⑧芦山地震滑坡编目，详细数据来源如表1所示。数据预处理包括地理坐标系统变换、图像配准、栅格数据矢量化、连续数据离散化等。为减少时间因素引发的影响因子与滑坡编目之间的矛盾，本文对基础数据进行了目视解译、判读及更新，以保证影响因子与滑坡编目之间的时间一致性。

表1 试验数据来源Table 1 Sources of experimental data

3 影响因子的选择及分析

3.1 影响因子的选择

根据影响因子的内在属性并结合文献资料[20-21]，本文将滑坡影响因子划分为4种模态：地震地质、地形地貌、地表覆盖和水文条件。

3.1.1 地震地质模态

地震峰值加速度：地面加速度和边坡重力叠加作用力在短时间内超过基岩附着力和摩擦强度引起边坡不稳定。地震滑坡分布与PGA密切相关，地震峰值加速度较大区域更容易发生滑坡。研究区滑坡分布与地震峰值加速度分布情况如图2(a)所示。

距断层距离：断裂构造带所处区域构造表面比较软弱，岩石风化严重，易形成深层的风化壳从而破坏斜坡稳定性。由地质构造运动形成的各组弱结构表面与斜坡自然环境或人类工程活动所形成的表面形成不同的构造组合，也是边坡失稳的内在因素。本文根据滑坡分布将距断层距离以1.5 km为间隔将研究区划分为7个部分，如图2(b)所示。

地震烈度：地震烈度是导致滑坡产生的主要动力因素之一，是衡量地震破坏程度的主要参数，地震烈度越大，地表所受破坏程度越大。研究区滑坡分布与地震烈度分级如图2(c)所示。

岩性：岩性决定了斜坡受破坏的难易程度，它是斜坡直接的物质组成基础，也是确定边坡强度、边坡变形、水理性质、应力分布等特征的基础。研究区的13种岩性分布与滑坡分布如图2(d)所示。

3.1.2 地形地貌模态

高程：高程是地形因素的主要代表，高程不同的区域局部集水能力不同，另外，人类工程活动强度在不同的高程上也有所不同。本研究根据滑坡分布将研究区高程划分为9个部分，如图2(e)所示。

坡度：坡度往往会影响边坡地表径流、应力分布、地下水补给和排水，进而改变滑坡的发育程度，是滑坡产生的重要因素之一。研究区滑坡分布与坡度分级如图2(f)所示。

坡向：坡向是指投影在水平面上的坡面的法向量方向。由坡向造成的地震滑坡存在差异性的主要影响因素包括地震波的传播方向、地壳运动方向以及板块运动方向等。同时，不同坡向区域受到外界环境的影响不同，如岩土体湿度、植被发育等，使得滑坡的孕灾环境在不同坡向上存在明显差异。研究区滑坡分布与坡向关系如图2(g)所示。

曲率：曲率反映了坡度变化程度，代表地面的复杂程度，会影响物质在斜坡上的运动状态(加速或减速)。通常，物质在凸坡和凹坡上比在平坡上更容易滑动，凸坡一般具有临空面且对地震波具有放大效应，其发生滑坡的危险性也更大。研究区滑坡分布与曲率分级如图2(h)所示。

地貌类型：滑坡的分布与地貌类型有关，滑坡往往发生在低山沟谷、黄土台塬以及丘陵地区，在平原地区不易发生。研究区地貌类型与滑坡分布如图2(i)所示。

3.1.3 地表覆盖模态

土地利用类型：不同土地利用类型对滑坡产生的作用主要在于边坡植被覆盖程度的不同。植被覆盖程度直接或间接影响地表蒸发、地表径流和入渗条件。同时，植物的根对土壤也有锚固作用。研究区土地利用类型与滑坡分布如图2(j)所示。

土壤类型：土壤是边坡材料的重要组成部分，不同类型的土壤具有不同植被覆盖情况、可塑性和透水性，其对滑坡的产生具有不同程度的影响。研究区土壤类型与滑坡分布如图2(k)所示。

距道路距离：距道路距离反映了人类工程活动对边坡稳定性的影响程度。在道路建设过程中，在斜坡顶部切割斜坡之类的工程活动会改变斜坡地形和强度，从而破坏斜坡结构的稳定性。研究区距道路距离与滑坡分布如图2(l)所示。

3.1.4 水文模态

距河流距离：距河流距离代表了斜坡受河流侵蚀作用的程度。河流对斜坡两岸具有侵蚀切割作用，会对坡脚产生扰动，从而破坏斜坡稳定性。研究区距河流距离与滑坡分布如图2(m)所示。

降雨量：降雨是滑坡产生的重要触发因素之一。在降雨过程中，地表水渗入斜坡，会增加斜坡重量；其次，雨水软化了滑动面，降低斜坡内物质间的摩擦力；同时，频繁的干湿交替作用易导致岩土体开裂，增加孔隙水压力，破坏极限平衡状态，为滑坡发生创造有利条件。研究区降雨量与滑坡分布如图2(n)所示。

地形湿度指数(TWI)：地形湿度指数代表了土壤中水含量的分布情况，土壤中水分含量会影响斜坡表面的岩石、土壤和植被状况，从而影响滑坡发育。研究区地形湿度指数与滑坡分布如图2(o)所示。

图2 本文使用的15种滑坡影响因子Fig.2 Fifteen causative factors used in the present research

3.2 影响因子分析

对于常规易发性评价模型，为防止影响因子的冗余信息对建模性能的影响，本文通过采用Pearson相关系数(Pearson correlation coefficient, PCC)对各影响因子间的相关性进行检验。PCC是衡量变量之间相关性程度的常用指标，其数值介于-1～1之间，PCC绝对值>0.5表示强相关[13]。

本文各因子间的相关性系数如表2所示，其中，C1—C15分别表示：地震峰值加速度、断层、地震烈度、岩性、高程、坡度、坡向、曲率、地貌类型、地表覆盖、土壤类型、距道路距离、距河流距离、地形湿度指数、降雨量。从表2可知高程与地震烈度、坡度、地貌类型和降雨量之间的相关性较大，降雨量与地震烈度和地貌类型相关性较大。此外，本文采用随机森林(RF)算法中的残差平方和对影响因子的重要性进行排序。从图3可知地震峰值加速度对该区域的滑坡具有最大影响程度，地形湿度指数影响程度最低。根据因子间的相关性系数和因子的重要性，剔除那些相关性系数大、重要性程度较低的影响因子。本文剔除与其他因子相关性较大的高程、降雨量2种影响因子，使用剩余13个影响因子作为对照组的输入特征。

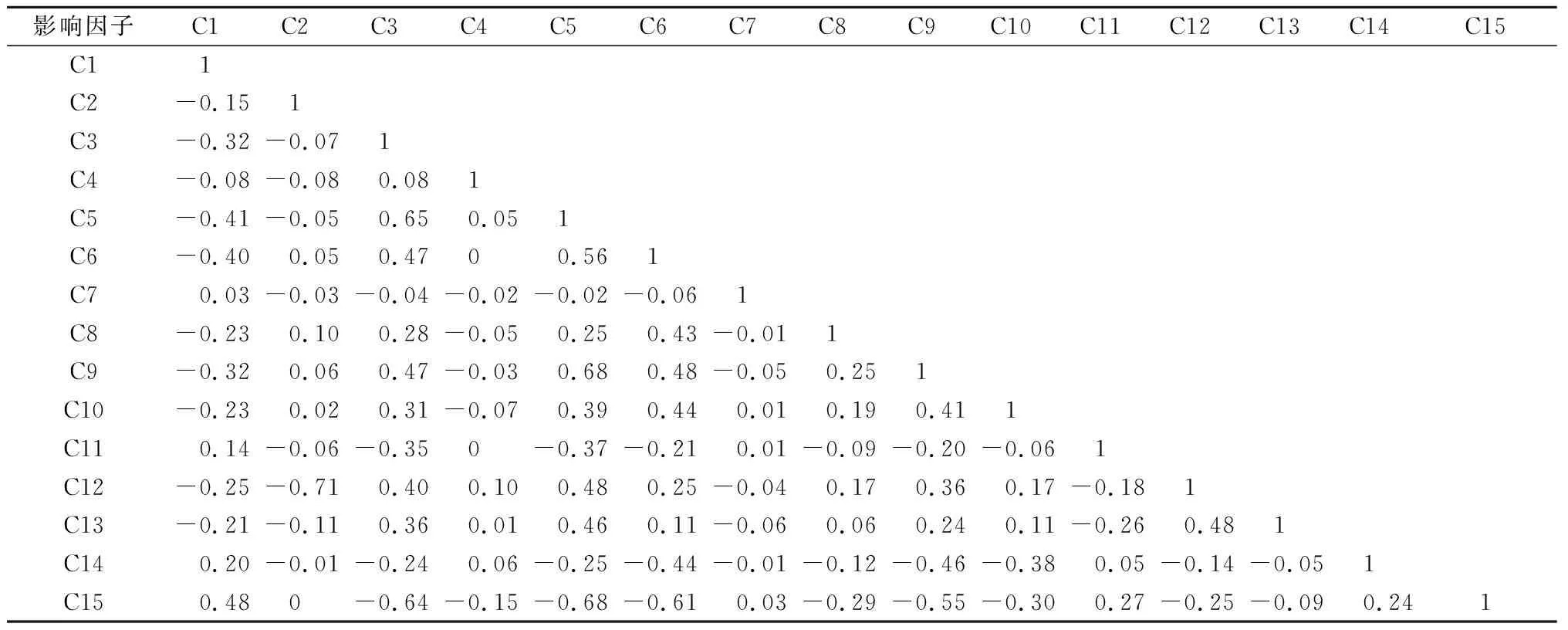
表2 影响因子间相关性系数Table 2 Coefficient of correlation between influence factors

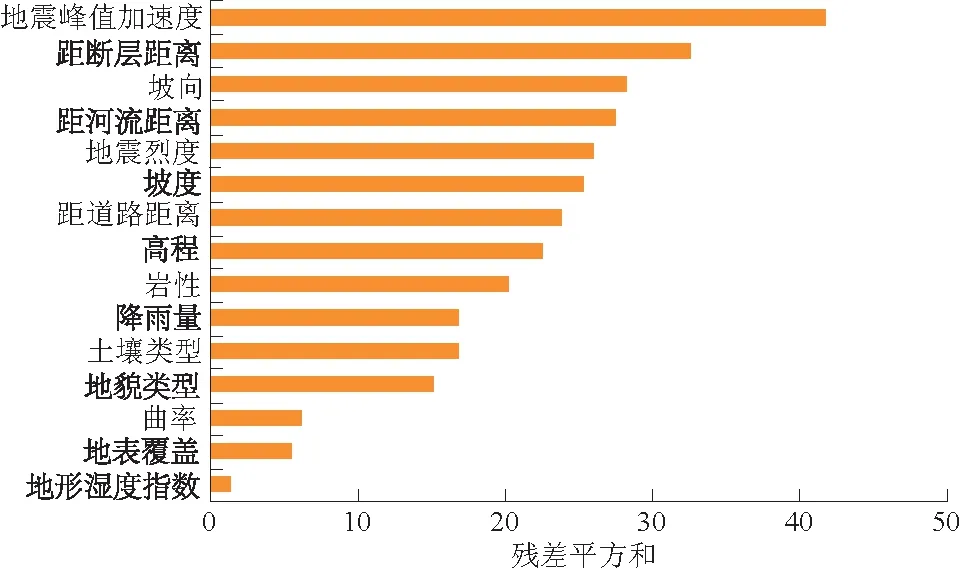
图3 影响因子重要性排序Fig.3 Ranking of the importance of landslide’s influence factors

4 多模态分类模型

4.1 确定数据模态并生成相似度图形

根据上文3.1节所述，本文将提取的15种影响因子划分为4种不同类型模态数据，分别为地震地质模态、地形地貌模态、土地覆盖模态和水文模态。对于其中任意一种类型模态数据所对应的L个特征数据，通过构建图Gi=(Vi,Wi)表征n个对象之间的关系，其中：i对应第i个模态；V代表n个对象；Wi是一个n×n的相似度矩阵；W(a,b)表示根据第i个模态数据的L个特征算出的对象a与对象b之间的相关性。由于随机森林可为多模态数据提取出一致的成对相似度，为组合不同模态数据提供了统一基准。因此，本文利用随机森林算法计算对象之间的相似度。

4.2 非线性图融合

4.2.1 相似度矩阵归一化

不同模态数据构建的图像Gi具有不同的Wi，融合不同模态数据本质上就是融合这些Wi。融合不同的相似度矩阵Wi，需要对其归一化。为避免归一化过程中Wi对角线上元素自相似性带来的数值不稳定问题，本文使用如下归一化方法：

(1)

4.2.2 相似度矩阵稀疏化

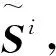
4.2.3 迭代交叉融合

(3)

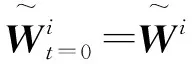
4.2.4 生成统一的图

(4)

其中m代表模态个数。

4.3 基于多模态分类的地震滑坡易发性制图

本文采用逻辑回归算法(Logistic Regression, LR)将统一相似度矩阵划分为不同滑坡易发性等级，方法流程如图4所示。

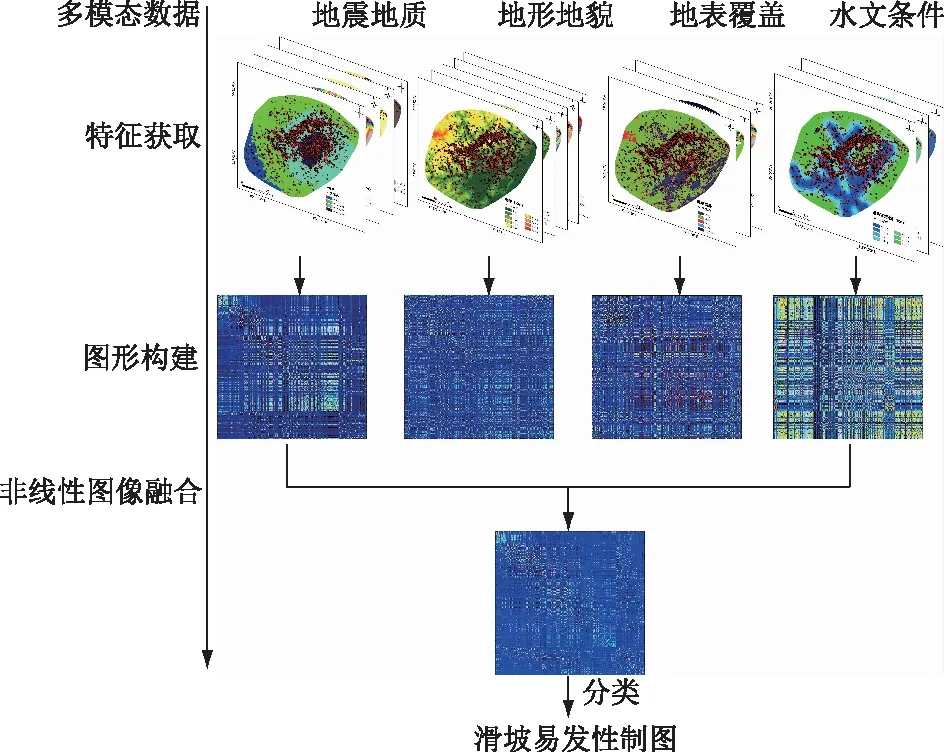
图4 基于多模态分类的地震滑坡易发性评价流程Fig.4 Flowchart of assessing seismic landslide susceptibility based on multimodal classification

5 地震滑坡易发性评价结果

5.1 评价单元确定

评价单元是进行滑坡易发性评价的基础步骤。目前，评价单元主要包含栅格单元、斜坡单元、地域单元、均一单元等[22]，其中，滑坡易发性评价中广泛使用的是栅格单元和斜坡单元。栅格单元具有数据处理简单、计算速度快等优点，然而，规则的栅格单元不能有效反映地质环境信息。因此，本文选择斜坡单元作为地震滑坡易发性评价单元。采用水文分析法，将研究区划分成2 373个斜坡单元。考虑到数据精度，将滑坡编目中面积>1 000 m2的4 541个滑坡点作为灾害点，参与地震滑坡易发性评价模型构建。由每个斜坡单元的滑坡点密度及目视解译，得到463个滑坡单元，随机选取等量的非滑坡单元共同构成样本数据。在样本数据中分别随机选择70%的数据作为训练数据，剩下的30%作为验证数据。

5.2 地震滑坡易发性制图

为对比本文方法和传统方法的性能，根据随机选取的训练样本，采用传统LR方法和基于多模态数据融合的MMC-LR方法开展地震滑坡易发性评价，分别得到2种模型的滑坡易发性指数，采用自然断点分类法将滑坡易发性指数划分为5个等级：极高易发区、高易发区、中易发区、低易发区和极低易发区，结果如图5所示。

图5 基于不同模型的滑坡易发性区划Fig.5 Zoning map of landslide susceptibility based on different models

将图5的滑坡易发性区划图与芦山地区实际分布的滑坡点叠加显示可以看出，同震滑坡点主要聚集在研究区中部，并向东北和西南方向延伸呈2条接近平行的条带状，2种模型得到的滑坡易发性区划结果与实际滑坡空间分布趋势较为吻合，区划结果具有一定的相似性，但在诸多区域存在差别。如在图中标注为F的区域中滑坡点分布稀疏，该区域在LR模型却被划分为极高易发区和高易发区，而在MMC-LR模型中该区域大部分被划分为中易发区和低易发区。另外，许多零散分布的滑坡点所在区域在LR模型未能被划分出来，如标注为A、B、C、D和E的滑坡区域在LR模型中被划分为低易发区，而在MMC-LR模型中被划分为极高易发区。

对此，分别统计2种模型区划结果中极高易发区和高易发区面积及其滑坡灾害点个数，得到LR模型结果为1 897.68 km2和3 598个，对应的MMC-LR模型结果为1 720.23 km2和3 857个，即MMC-LR模型对比LR模型更小的区域中有更多的滑坡点。总体而言，MMC-LR模型的滑坡易发性区划结果比LR模型的结果具有更为针对性的区划效果。

5.3 模型精度评估与比较

为定量比较不同评价模型的性能优劣，以特异性为横轴、以敏感性为纵轴绘制出受试者工作特征(Receiver Operating Characteristic,ROC)曲线，该曲线反映了不同阈值下模型的综合性能。对于不同模型的ROC曲线，当曲线下面积(AUC)值越接近1时，模型的精度越好。LR模型和MMC-LR模型的ROC曲线如图6所示，MMC-LR模型的AUC值为0.860，LR模型的AUC值为0.818，MMC-LR模型显示了更好的易发性评价性能。

图6 LR模型和MMC-LR 模型的ROC曲线Fig.6 ROC curves of LR model and MMC-LR model

将研究区滑坡灾害点与易发性区划图进行叠加分析，统计2种模型各等级易发性区划面积、区划中滑坡灾害点数和滑坡点密度,如表3、表4所示。由表3可知,LR模型中极高-高易发区面积占整个研究区面积的35.17%，滑坡点数量占总滑坡数量的79.23%;由表4可知,MMC-LR模型中极高-高易发区面积占整个研究区面积的31.88%，滑坡点数量占总滑坡数量的84.94%。

表3 LR模型滑坡易发区划统计Table 3 Statistics of landslide susceptibility zones obtained by LR model

表4 MMC-LR模型滑坡易发区划统计Table 4 Statistics of landslide susceptibility zones obtained by MMC-LR model

在2种模型得到的滑坡易发性区划结果中，滑坡点密度随着滑坡易发性等级的升高而增加，在极高易发区中滑坡点密度达到最大值，这与实际认知相符，从侧面反映了评价结果的合理性。相较于LR模型，MMC-LR模型在极低易发区、低易发区和中易发区滑坡点密度较LR模型低，而在高易发区和极高易发区中高于LR模型。这再次说明滑坡点在MMC-LR模型的易发性区划结果中的分布比在LR模型中的分布更具有针对性，MMC-LR模型的区划结果更为合理和可靠。