滑坡涌浪近远场划分及其水波特性分析

2022-05-19张少强黄筱云程永舟沈保兴

长江科学院院报 2022年5期

张少强，黄筱云,2，程永舟,2，沈保兴

(1.长沙理工大学水利工程学院，长沙 410114； 2.长沙理工大学水沙科学与水灾害防治湖南省重点实验室，长沙 410114)

1 研究背景

水库和河道的边坡长期受到水体的浸润作用，极易使得边坡失稳发生滑坡，滑坡体以一定速度冲入库区或河道等水体中，在极短的时间内冲击水体，造成水位迅速抬升形成涌浪。涌浪将沿着水库及河道进行传播，对沿途的涉水建筑物和居民生命财产安全构成巨大的威胁；同时，涌浪在航道上横向与纵向的传播会对沿途船舶构成一定的威胁。因此，对滑坡涌浪的产生与传播特性展开更为深入的研究，对于灾害风险的评估、库区的运营管理以及如何科学、有效地降低滑坡涌浪灾害损失具有重要的工程实际意义[1]。

近年来，随着全球气候变化，滑坡涌浪灾害日益频发。为防止和减轻滑坡涌浪带来的巨大破坏，国内外许多学者对滑坡涌浪灾害进行了大量的深入研究。滑坡涌浪按其发展变化的复杂过程，可以分为涌浪的产生、传播、爬高3个阶段。近场区域内涌浪的非线性程度高，具有极强的破坏力，滑坡涌浪最大波面高度往往出现在近场区域内。国内外学者通常把涌浪波高作为决定滑坡涌浪灾害强度的重要参数，如：Noda[2]基于单向流研究，在半无限水体中考虑2种极端条件下的滑坡体运动，垂直下落与水平推动，基于产生表面波得出涌浪最大首波计算公式；1980年，潘家铮[3]在考虑滑坡体垂直下落和水平推移的2种极限条件下，分析涌浪反射与叠加的特点，提出潘家铮法用来计算滑坡涌浪的初始涌浪高度。早期研究注重于对涌浪高度的公式推导，主要为了解决在工程实际中的安全问题，为其提供一定的经验公式作为依据；Wiegel[4]为探究滑坡涌浪波高与各个影响因素之间的关系，选取滑坡体淹没深度、水深、质量、滑坡体长度和滑动面倾角作为变量，展开物理模型试验，试验结果表明，涌浪波幅关于滑坡体质量、滑动面倾角、水深成正比，而与滑坡体淹没深度成反比；孔增增等[5]应用计算流体力学软件FLOW-3D对V型河谷滑坡涌浪进行数值模拟，考虑了5个相关因素，拟合了V型河谷最大波面高度的公式；韩林峰等[6]建立水库滑坡涌浪三维物理模型，利用获得的试验数据与理论计算结果，基于动量平衡理论推导出静水、波动条件下涌浪最大近场波幅的理论表达式。涌浪在传播过程中可以分为近场区域和远场区域，涌浪在产生之后经过一定距离的传播后，进入远场区域，受其弥散作用的影响，在远场区域内，涌浪波高大幅降低，波浪的非线性减弱，与近场涌浪相比破坏力较小。袁培银等[7]根据三峡库区实地调研结果设计物理模型试验，对三峡库区的岩体滑坡涌浪的传播与衰减规律进行了研究，结果表明，滑坡断面、直道和过弯直道3个区域涌浪的最大波高、衰减程度随着传播距离的增加而减小；Biscarini[8]通过FLUENT软件模拟了滑坡体冲击水体产生涌浪并传播的全过程；Risio等[9]进行三维水池试验，通过测量波浪爬坡高度，分析涌浪的爬坡特点和传播特性，得出在滑坡体与水体发生相互作用的区域，波高随传播距离的增大呈增大趋势，在滑坡体宽度2倍范围之外波高开始衰减；岳书波等[10-11]通过模型试验将滑坡体入水形成涌浪的全过程和涌浪传播过程中的水位变化进行了记录，非常直观地展示了涌浪的初始运动形态特征和衰减变化规律。

综上所述，研究成果集中在滑坡涌浪的产生及传播过程等方面，而对于滑坡涌浪近场与远场水波特性分析的数值模拟研究相对较少。本文以数值模拟的方法研究不同密度的刚性块体入水过程，结合相关物理模型试验对所建立的数值模型进行验证，对固体滑坡涌浪的近场和远场波浪特征进行描述与比较，可为工程防灾、减灾提供科学依据。

2 控制方程与数值求解方法

为模拟滑坡涌浪过程和分析涌浪的水波特性，引入FLOW-3D[12]软件进行建模、计算与分析。基于物质守恒、动量守恒和能量守恒原理，针对FLOW-3D的计算域，通过有限差分法对其进行离散化处理，以获得瞬态三维解，解决多尺度、多物理场的流动问题。

FLOW-3D采用FAVORTM与流体体积法( Volume of Fluid，VOF)技术可求解非牛顿流体、孔隙介质流、表面张力效应、两相流等的三维瞬态N-S方程，从而得到真实精确的自由表面流场数据。FAVOR和VOF的技术运用，在定义欧拉网格中的固体边界和追踪流体计算的相应固体边界上有了新突破，并实现了实体网格的自由生成、几何形状的快速准确定义。

2.1 控制方程

在FLOW-3D数值计算中，连续性方程为

(1)

式中：VF为可流动流体的体积分数；u、v、w分别为速度矢量在x、y、z方向上的分量；Ax、Ay、Az分别为x、y、z方向上单元网格面中流体区域的面积分数；R为紊流扩散系数；ρ为流体密度，本文研究对象为水，取值为1 000 kg/m3；RSOR为质量源项；RDIF为湍流耗散项，其表达式为

(2)

其中，

vρ=Scμ/ρ。

式中：μ为动量扩散系数(即黏度)；Sc为常数，其倒数通常称为紊流施密特数。

2.2 动量方程

流体速度分量(u、v、w)在3个坐标方向上的运动方程为带附加项的Navier-Stokes方程，即：

(3)

(4)

(5)

式中：Gx、Gy、Gz分别为物体在x、y、z3个方向的重力加速度；fx、fy、fz分别为物体在x、y、z3个方向的黏性加速度；vρ为动力扩散项，uw、vw、ww为质量源分速度；us、vs、ws为流体在源表面的相对速度；bx、by、bz分别为流体穿过多孔介质后在x、y、z3个方向的水头损失，最后一项为质量源项；p为流体中某一点的水压力；ξ、δ均为连续性方程的修正系数。

2.3 湍流模型

FLOW-3D提供了5种湍流模型,包括标准的k-ε模型、RNGk-ε模型、ε方程模型、普朗特混合长度模型和大涡模拟。针对一般情况下，运动要素变化不大的常规流体，使用标准的k-ε模型可以较好地模拟其流体的运动特征变化情况。但由于本文所建立的数值模型需要模拟滑坡涌浪的产生以及传播规律较为复杂，滑坡体下滑时会导致局部水体产生巨大的变形，故采用RNGk-ε模型进行三维数值模拟计算。

RNGk-ε两方程模型的使用与k-ε单方程模型非常相似，其差别在于模型中的系数与常数有所不同，在标准k-ε单方程模型中的方程系数与常数项是根据经验确定；而在RNGk-ε双方程模型中，不论是方程系数还是常数项均得到了明确的推导。RNGk-ε双方程模型中自定义参数RMTKE(用于计算湍流扩散系数的黏度乘数)、CDIS1、GUN(可调的无量纲参数)默认值分别为1.39、1.42、0.085，根据湍流动能项KT和湍流产生项PT计算得到CDIS2。一般来说，RNGk-ε双方程模型比k-ε单方程模型具有更广泛的适用性，特别是在刻画低强度湍流运动和强剪切区域流动时具有独特的优势。

3 模型验证与工况设置

为验证数值模型的有效性，借用Liu等[13]的物理模型试验作为参照来设计数学模型，以完成对其试验的复现。在其物理模型试验中，滑坡体长度为0.914 m，高度为0.457 m，宽度为0.653 m，滑坡体高于静水面0.454 m。所使用的物理水槽长为104 m，宽3.7 m，高4.6 m，水深为3 m，倾斜岸坡坡度为26.6°。图1为三维物理模型试验的照片以及平面布置示意图。

图1 物理模型试验照片和平面布置示意图Fig.1 Photo of physical model test and plane layout

3.1 模型自由波面对比

模拟计算得到结果同Liu等[13]的模型试验结果的自由波面高度相近，如图1(b)所示。测点坐标(x，y)分别为4#(1.83,0)、5#(2.74,0)、6#(1.83,-0.635)、7#(2.74,0.635)、8#(0.482 6,1.092)、9#(0.863 6,1.092)、10#(1.244 6,10.92)、11#(0.482 6,0.635)、12#(0.863 6,0.635)、13#(1.244 6,0.635),数值单位均为m。由图 2可见，本文所建立数学模型的数值模拟结果与Liu等的试验结果吻合较好。

图2 4#—13#测点自由波面对比Fig.2 Comparison of free wave surface of 4#-13# points

3.2 工况设置

建立滑坡涌浪模型如图3所示，计算域滑坡方向长为65 m，宽50 m，高17 m，静水深h=8 m，岸坡倾斜角度θ=45°。Heller等[14]表明滑块形状对涌浪最大高度影响不大，滑块采用断面为等腰直角三角形的三棱柱，滑坡体宽度ls=10 m保持不变，滑块总体积Vw随着断面边长b取值而变化，分别取值4、5、6 m。初始时刻滑块中心位置为25 m，滑块下端与静水面平齐，v为滑坡体初始下滑速度，分别取值为3、4、5 m/s。表1给出了27组数值模拟试验所设定的参数，其中水下运动时间为测量值，不可在试验前获知。

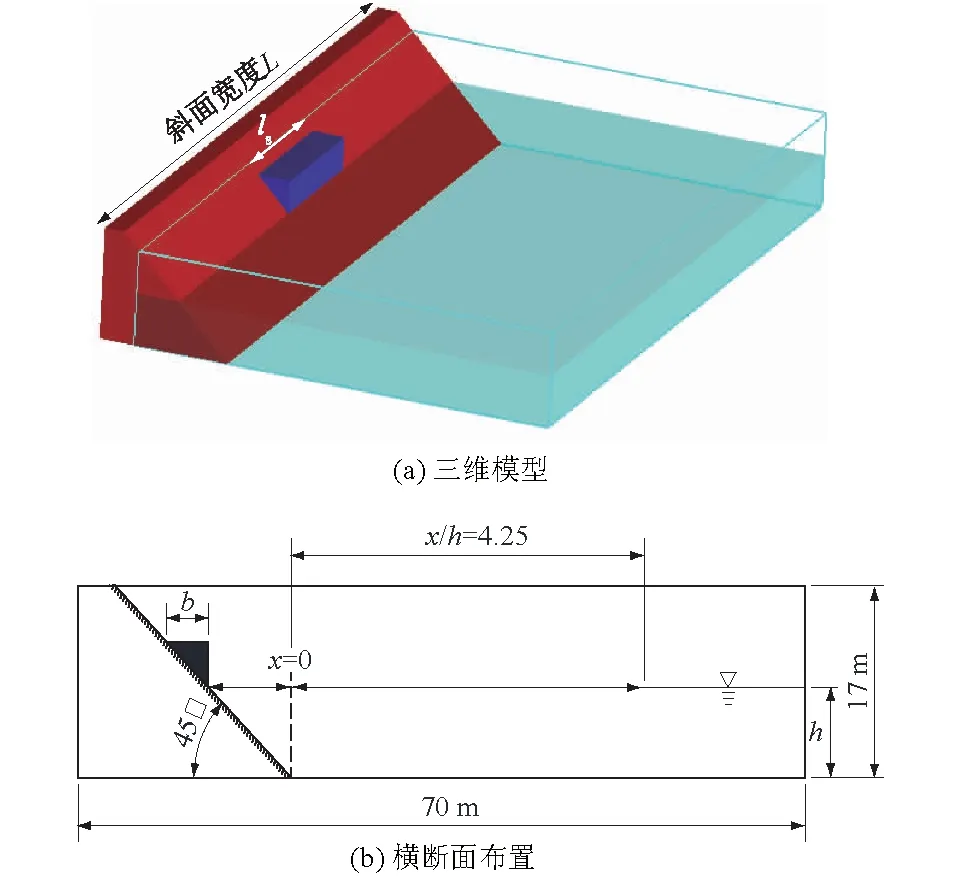
图3 三维模型及横断面布置示意图Fig.3 Schematic diagram of 3D model and layout of cross section

表1 数值试验工况设计Table 1 Design of numerical test conditions

滑坡涌浪数值模拟的结果受到求解方程、网格、边界条件等多方面的影响，其中网格的质量对其模拟结果的影响最为明显。为保障模拟结果的可靠性，计算域内采用正交的正六面体网格，其网格大小分别为0.5 m×0.5 m×0.5 m、0.4 m×0.4 m×0.4 m、0.3 m×0.3 m×0.3 m，采用3种不同尺寸的网格进行模拟计算，取其结果的平均值[15]。

4 滑坡涌浪的水波特性分析

4.1 近场涌浪特性

近场起始位置为斜面底部趾端位置如图 3(b)所示，并定义该位置为x/h=0。如图4所示，展示了不同密度滑坡体在近场x/h=0位置的涌浪时程曲线。结果表明，滑坡体冲击水体所产生涌浪的首波波高关于滑坡体密度呈正相关，因为密度越大的滑坡体入水时所携带的动能更大。

图4 x/h=0处不同密度滑坡体的近场涌浪时程曲线对比Fig.4 Comparison of time-history curves of near-field wave obtained at x/h=0 among landslide mass with vaired density

3种工况下的波浪曲线存在细微差异，但每条波浪曲线的特征均非常相似：滑坡体以一定速度冲击入水，由于具有较快的速度，入水点附近水体在滑块入水速度的冲击和滑块体积的侵占作用下向外加速运动；但受到周围静止水体的阻碍，则会向水面上方运动，产生水体的局部雍高，使得滑坡体正前方水体受到滑坡体的推挤向上运动形成波峰。同时滑坡体的下滑运动导致水体产生空腔，使得滑坡体上方水体液面下沉形成波谷。随着滑坡体的进一步下滑，滑坡体正上方形成空腔，周围水体涌入其中，激起水体自由表面的反复振荡，形成波幅不断衰减的波列向外传播。滑坡体冲击水体所生产涌浪的首波峰振幅略大于首波谷，滑坡体冲击水体所产的涌浪具有很强的色散性，涌浪在形成首浪之后转变为频率更高振幅较小的波浪进行传播。同时由图4可知，在x/h=0处，密度越小的滑坡体所产生涌浪的波长越小。

图5表示涌浪在计算时间内的全时程和首浪时程曲线(组次11，ρ=2 350 kg/m3)。涌浪全程势能能量公式与滑坡体入水动能公式[16]分别为：

图5 近场涌浪时程曲线Fig.5 Time-historiy curves of surge height at near field

(6)

(7)

式中：Ep(x/h)表示x/h处涌浪的势能；b为滑坡体宽度；ρw为流体密度；c为波速；Es表示滑坡体初始动能；v为滑坡体入水速度。将首波势能关于涌浪全程势能作比即为首波占总的涌浪势能的大小，实现对目标测点位置首浪能量的度量，展示其涌浪波首波特性。

在工况11中，当滑坡体密度为ρb=2 350 kg/m3时，计算无量纲全程涌浪势能Ep(0)/Es=1.614×10-3和无量纲首浪势能Eη/Es=1.194×10-3，两者之比Eη/Es=0.7Ep(0)/Es。图6为各工况下x/h=0处涌浪全程势能与涌浪首波势能的关系。通过幂函数对多组数据并置拟合，得到涌浪首波涌浪势能Eη与全程涌浪势能Ep(0)变化的函数关系为：Eη/Es=0.7Ep(0)/Es，拟合系数R2=0.99。

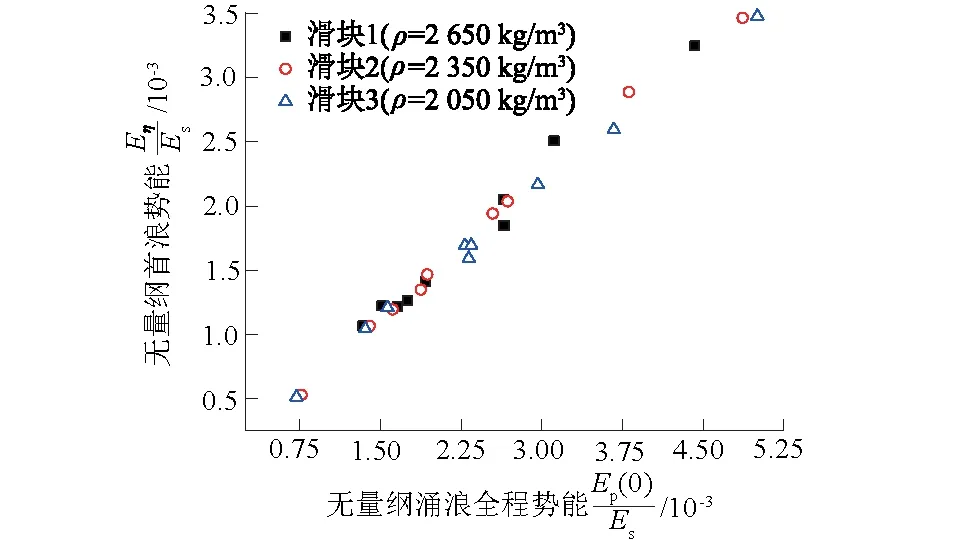
图6 首波势能与全程势能的关系Fig.6 Relationship between the first potential wave energy and the whole potential energy

图6中，涌浪首波势能Eη和全程涌浪势能Ep(0)存在明显的线性关系，试验结果表明在x/h=0处滑坡涌浪首波势能占全程涌浪势能的70%左右，且与滑坡体密度无关。

4.2 远场涌浪特性

图7为距离涌浪产生处较远的x/h=4.25处所记录的涌浪时程曲线，涌浪的传播表现为波列的色散特性，同时涌浪以小振幅水波进行传播，符合线性水波标准[17]。远场涌浪波形由一个前导波和其后续波列组成，且前导波和后续波列的振幅较小。前导波由滑坡体冲击水体时对水体做水平的推进运动作用而产生，滑坡体密度越大，则产生的涌浪前导波振幅越大。

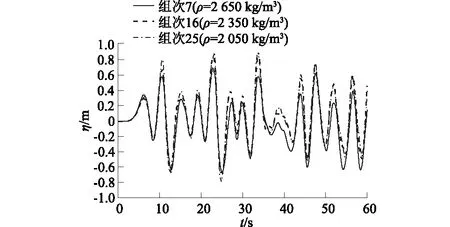
图7 远场x/h=4.25处涌浪高度时程曲线Fig.7 Time-history curves of surge height at far fieldx/h=4.25

计算涌浪在远场处的主波长之前，需要对涌浪的主周期进行预测，该周期对应于滑坡体入水所产生的线性水波频率较高的频谱。利用快速傅里叶变换对x/h=4.25处的涌浪时程曲线进行变化处理，其结果如图8所示，远场处的涌浪振幅关于滑坡体密度存在负相关关系，但各个工况所展示的频谱均非常相似，其涌浪主频率f≈(0.21±0.01)Hz，计算得出该位置处涌浪的主周期为T0≈5.0 s。基于27组滑坡体水下运动时间的平均值为2.5 s，定义涌浪周期以t0≈2.5 s为选定的特征值，可将远场涌浪主周期近似为T=2t0。

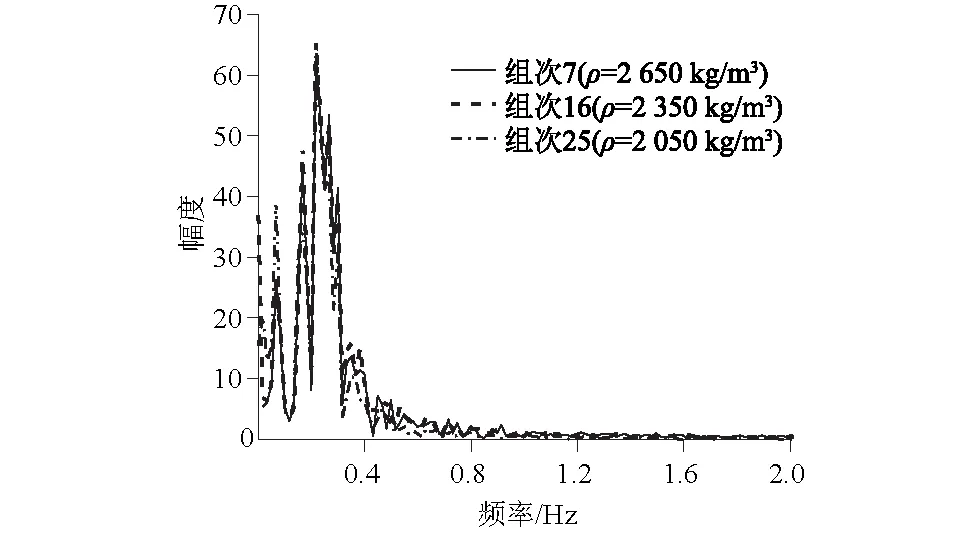
图8 各工况下远场涌浪傅里叶变换Fig.8 Fourier transform diagram of far field surge under various working conditions

涌浪自近场传播至具有恒定水深的远场区域，在其传播过程中，涌浪的波浪类型会呈现出具有特定波长的2种波浪形式：中等水深波与浅水波[18]。忽略波浪发生浅水变形的情形，即远场涌浪的主波长λd为

(8)

式中：t0为远场涌浪周期；g为重力加速度；h为水深。

4.3 远场涌浪起始位置判定

探讨涌浪在传播过程中不同位置处的能量关系，根据结果，提出远场起始起点位置的判断依据。涌浪在传播过程中，不考虑波浪破碎的情形下，能量的消耗在其传播过程中几乎没有。由于其线性波列所具有的色散特性，导致以群速度进行传播，而非以单波的波速传播，而涌浪是波能的一种物理表达形式。对x/h位置处总的波浪势能进行计算可知，滑坡所产生的涌浪中，可能存在一部分驻波，其波能被束缚在近场范围内，无法向外进一步传播。同时，涌浪在近场区域内的能量总值保持为一恒定值，动能与势能相互转换维持稳定。运用式(6)计算不同位置处的涌浪势能，随着涌浪传播时间与距离的推移，自由液面也将趋向于静止。图9为无量纲涌浪势能Ep/Es关于x/h的变化。

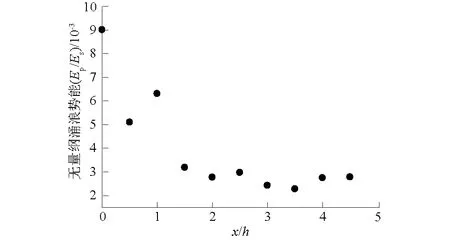
图9 无量纲涌浪势能Ep/Es随距离x/h的变化Fig.9 Change of dimensionless potential wave energyEp/Es with distance x/h

由图9可知，在近场范围内即涌浪产生区的能量是远场处涌浪能量的2倍以上。但是涌浪从近场传播至远场过程中，总能量将会小于线性波传播至远场势能的2倍。根据计算结果推理，在近场范围内20%左右的波能以驻波的形式存在，其余的能量均以势能形式继续向外传播。

对于x/h>1，在涌浪传播过程中大量的势能被转化为动能，直至传播至无穷远处使动能与势能处于均分平衡状态，无量纲涌浪势能Ep/Es=2.5×10-3保持恒定，因为在远离涌浪产生区的线性水波的动能与势能是相等的[19]。涌浪能量积分达到最大值之后，涌浪能量向平稳过度的过程中，将会出现一处涌浪的势能与动能相等的位置附近[15]。由图9可知，x/h=1.5～2.0为第一次涌浪势能与动能相等的位置，取其平均值作为远场涌浪起始位置，即x/h=1.75，此位置即判定为滑坡倾斜角度为45°、水深为8 m的陆上滑坡涌浪远场传播开始的位置。因此，前文所述的位于x/h= 4.25的涌浪数据可以作为测量远场涌浪传播的信息。