冰上石笼自然沉排的冰热力学和力学理论及应用
2022-05-19李春江李志军王庆凯张宝森
李春江,李志军,杨 宇,王庆凯,张宝森,邓 宇
(1.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2.沈阳工程学院 基础教学部,辽宁 沈阳 110136;3.黄河水利委员会 黄河水利科学研究院,河南 郑州 450003;4.水利部堤防安全与病害防治工程技术研究中心,河南 郑州 450003)
1 研究背景
利用寒区结冰河道,实施冰上石笼沉排是一种因地制宜且有效的河道岸坡防护技术[1],它分为自然沉排和强迫沉排。自然沉排主要等待春季气温升高,冰层升温和融化,石笼排体自然沉入河底;强迫沉排主要依靠人工破冰沉放石笼排体。1980年以来,中国东北地区河流相继应用冰上石笼自然沉排(以下简称“石笼沉排”)技术,例如:1986年在辽河的二龙眼、兰旗、李河套、平安堡和杨家窝5 处应用冰上石笼沉排实施护岸工程[2];1998年冬季在松花江的苏家工程600 m 崩岸段采取40 cm 厚石笼沉排护岸[3];2003年3月在嫩江白沙滩险工处布放宽度15 m,总面积49 500 m2石笼沉排[4]。钟华等[5]系统总结了冰上石笼沉排的制作、连接、锚固、压载和沉放等工艺。汪恩良等[6]综述冰上石笼沉排在寒区护岸工程应用的研究进展。总的来说,冰上石笼沉排施工首先方法简单,易掌握,节约投资;其次,具有良好的整体性和柔性,能很好自适应边坡及河床地形起伏,防护效果好。
冰上石笼沉排的工程应用涉及冰层承载力,冰层承载力是以板壳力学为基础发展起来的,国内外已有相关报道。中国学者1986年在辽河开展了不同冰厚条件下冰上石块压载试验,得到冰厚与极限荷载的关系曲线[2]。张栋[7]利用低温试验室内水槽开展了12 组室内悬臂梁试验,得到冰层平均弯曲强度为842.5 kPa,还模拟了冰上石笼自然沉排和强迫沉排的下沉过程。李吉庭[8]利用ANSYS 软件开展不同冰层厚度的承载力数值模拟。冰层自重同水位波动联合作用下的冰层开裂或破碎也是承载力问题,已被国内学者关注[9-10]。同样冰上娱乐[11]和冰上交通[12-13]也有涉及冰层承载力。国外学者Wyman[14]在1950年研究加拿大湖冰承载力时,分析了集中荷载和均布荷载下的承载力理论模型。Frederking 等[15]推导出冰层应力与应变关系,指出海冰静荷载承载力的安全条件是冰层最大挠度不超过干弦高度。Sinha 等[16]发展了包括冰晶结构、时间和温度三因子的淡水冰短期弹性-黏弹性承载力模型。Kerr[17]总结了短期静荷载、长期静荷载和移动荷载3 种工况的冰层承载力试验成果。到21 世纪,Beltaos[18]从应力、挠度/应变、应变能和尺寸效应讨论了浮冰承载力的失效准则,并利用5 组试验数据进行检验。Masterson[19]介绍在钻井、管道运输工程中不同荷载类型下计算冰层极限承载力的方法。Weale 等[20]以南极冰上补给运输为背景,从最大拉应力和最大挠度两方面评估了McMurdo 站在4 个海冰表面温度区间(-4~-10 ℃、-10~-20 ℃、-20~-27 ℃、<-27 ℃)的冰层承载能力。国内外关于冰层承载力的研究已取得丰硕成果,但未见有将冰热力学与冰力学耦合来评价冰层承载力的成果。
2020—2021 年冬季围绕黄河冰上石笼自然沉排,开展了以下工作:(1)获取黄河什四份子弯道整个冰期连续气象要素和雷达监测冰厚数据;(2)钻孔实测石笼沉排施工区域冰厚;(3)现场布放铅丝石笼和摆放已知质量的石块;(4)观测石笼沉排期间的冰面变形。具体思路是:(1)利用现场连续监测气象和冰厚数据,确定冰-水界面平均热通量,在此基础上,计算石笼沉排下冰温;(2)利用热力学获得的石笼下冰层温度和力学试验获得的冰弯曲强度、弹性模量与温度关系,计算冰层相应的承载力;(3)利用石笼周边冰面变形和冰力学中的长期强度概念,获得冰力学中承载力衰减指数;(4)利用热力学获得的关键参数冰-水界面平均热通量和力学获得的黄河冰长期承载力衰减系数,以形成用于评估石笼沉排铺放后的冰层承载力计算式,为黄河实施冰上石笼沉排提供科学依据。
2 冰上石笼沉排现场试验
2.1 研究区概况黄河什四份子弯道(图1)位于内蒙古托克托县境内(111°2′53″E,40°17′39″N),它是典型的“Ω”型弯道,河道比降约0.1%,河宽200~600 m,海拔991.8 m[21]。

图1 黄河什四份子弯道试验现场
每年11月中旬至翌年3月中旬,该河道将经历流凌-封河-开河凌汛过程,河道流量变化较大。2020—2021年凌汛期河道流量362~1270 m3/s,什四份子弯道实测最大冰厚90 cm,平均水深7.8 m,冰下平均流速0.5 m/s。2021/1/20 现场查看,什四份子弯道凹岸护岸滑塌,出现宽约0.07 m 纵向裂缝,岸坡下滑深度0.6 m。封河期该弯道凹岸经常形成冰塞体,河道断面进一步缩窄[22],流速增大,凹岸河床容易发生冲刷,开河期退水阶段护岸工程有继续滑塌风险,因此开展冰上石笼沉排试验,防止岸坡再次滑塌。
2.2 冰上石笼沉排试验过程2021/1/24—2021/1/26 开展冰上石笼沉排试验,石笼沉排铺放方式如图2。每一石笼沉排单元的长×宽×高为6 m×2 m×0.5 m,石笼沉排单元内每隔2 m 设置一个铅丝隔断。采用宾格石笼串联方式,计划铺放15 组,但因冰面提前开裂,实际铺放9 组。具体实施时,吊车将块石从岸边投放到网笼内,人工进行石头整平和石笼封装,从上游向下游依次铺放。根据现场称重测量确定石笼体平均密度为2200 kg/m3。在图2 设计铺放的石笼沉排四周安置5 个冰面变形观测点,在每个变形观测点处钻洞,插入并冻结一根木桩,保证木桩与冰面相对静止。在木桩侧边钉一颗钉子,利用全站仪观测钉子的高程。2021/1/24 9∶00 开始施工,2021/1/26 16∶00 黄河水沿着冰裂缝溢出,部分石笼沉排下沉被水淹没。
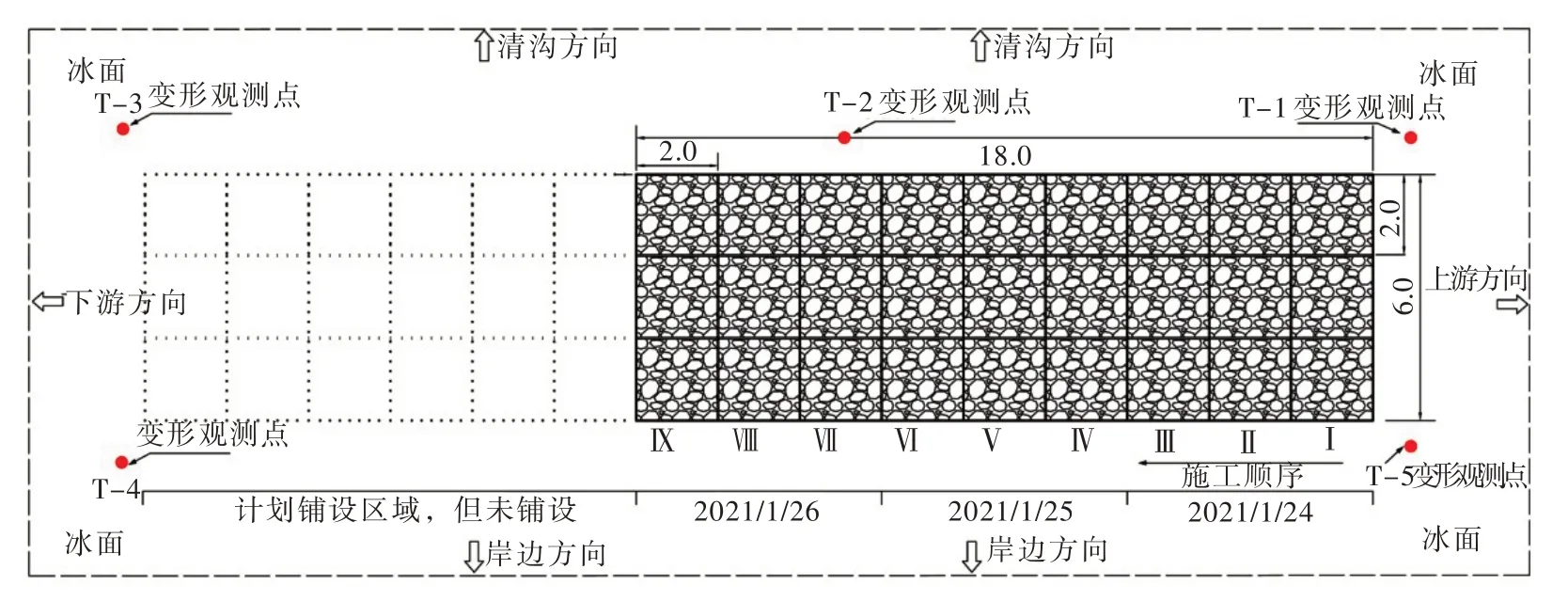
图2 冰上石笼沉排铺放和冰面变形观测点平面图(单位:m)
2.3 数据监测及采集2020—2021年冬季,首先利用图1(a)B 点的非接触式冰厚雷达系统[23]获取B点整个冰期的冰厚和冰面高程数据,设计精度0.01 m。试验A 点距离B 点70 m,距离头道拐水文气象观测站(C 点)3100 m。C 点长期记录气温、气压、湿度、风速和风向等气象数据。B 点和C 点的记录频率均为1 h。石笼沉排铺放时刚刚处于黄河融冰期,铺放处钻孔实测冰厚60 cm。试验期间,利用全站仪每天观测1~2 次石笼沉排周边5 个冰面变形观测点的高程变化,精度为±2 mm。
3 冰上石笼沉排的冰热力学理论和关键冰参数确定
3.1 冰热力学描述当石笼沉排铺放到冰面,石笼沉排下的冰内热量交换发生改变。由于石笼沉排的颜色和厚度,一般起到保温作用。20 世纪末发展的一款一维高分辨率气-雪-冰-水热力学数值模式(简称HIGHTSI)[24-25],它比只能计算冰厚度的斯蒂芬热力学模型或者修正的各种斯蒂芬表面能量平衡模型精度高[26-27],并且既能模拟冰的生消过程,又能给出冰内温度。当冰-水界面热通量归一化为常量后,该模式简洁,物理涵义清晰。另外它与国内发展的水库冰热力学模型[28],河冰热力学模型[29]原理上基本相同,只是参数化方案的选择差异。这对短期冰的生消模拟差异不大,但不能用于整个冰期的河冰生消过程。本文作者曾多次成功地将HIGHTSI 模型应用于中高纬度的湖冰和极地海冰,所以采用HIGHTSI 作为黄河冰石笼沉排的冰热力学过程模拟。一般来讲黄河宁蒙段冰面积雪存留时间很短,本文模拟计算时假设河冰上无积雪。冰面铺放石笼沉排后的冰温是评估冰层承载力的依据,因而不能采用石笼沉排外围的冰内温度,对石笼沉排的外围冰面采用气-冰-水三层结构热力学模型;对石笼沉排下冰层采用气-石-冰-水四层结构热力学模型。二种结构的热力学平衡示意图由图3 给出。由于HIGHTSI 模型及其参数化方案在国内冰研究中有详细介绍[30],具体细节不再叙述,仅给出该模式计算关键参数的取值。
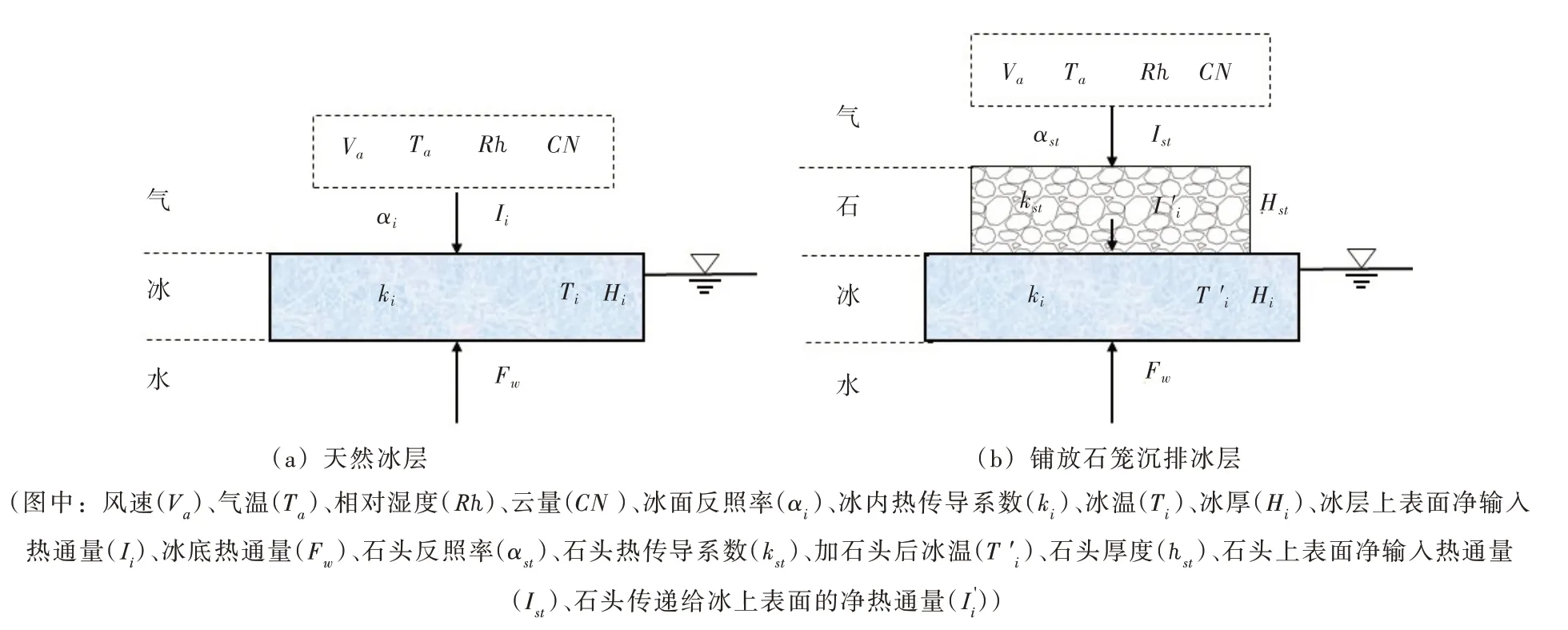
图3 二种情形热量平衡示意图
(1)石笼沉排外围冰层热平衡方程思想:在风速、相对湿度、云量、辐照度(冰面反照率影响)和气温联合作用下产生的净热通量Ii向下输入冰层,冰-水界面热通量Fw向上输入冰层。

(2)有石笼沉排时冰层热平衡方程思想:在风速、相对湿度、云量、辐照度(石头反照率影响)和气温联合作用下产生的净热通量Ist向下输入石头层,在石头热传导率kst影响下,传递到冰层上表面的净热通量I′i再向下输入冰层内,冰-水界面热通量Fw向上输入冰层。

利用HIGHTSI 模型开展冰厚和冰温模拟计算,所涉及关键参数取值见表1。
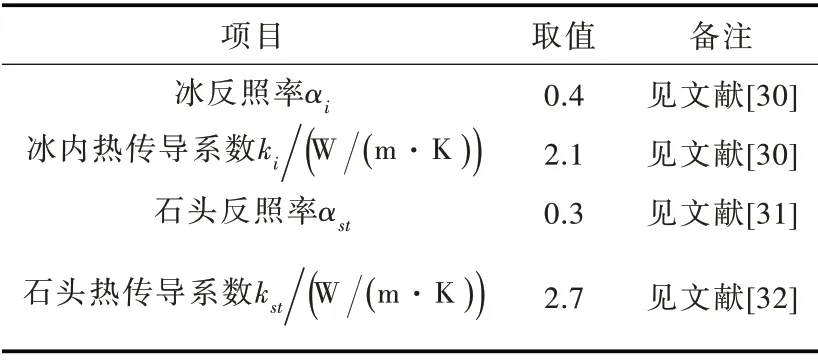
表1 HIGHTSI 模式关键参数取值表
3.2 冰-水界面热通量的确定冰-水界面热通量Fw是HIGHTSI 模式中关键热力学参数,应用中需要首先确定适用于黄河宁蒙段的归一化冰-水界面热通量,之后利用优化后冰-水界面热通量输入HIGHTSI 模型计算冰温,冰温将作为冰力学计算的输入参数。
以冰-水界面热通量(Fw)为辨识参数,构建观测冰厚与HIGHTSI 模拟冰厚差值最小为目标的最优辨识模型,见式(3)和式(4),确定冰-水界面热通量。根据已有湖冰冰-水界面热通量观测结果3~10 W/m2[30],黄河冰底因水流流动冰-水界面热通量可能会有所增加,因此本文以FW=[0,15]为冰-水界面热通量辨识范围,辨识间隔为0.01 W/m2。
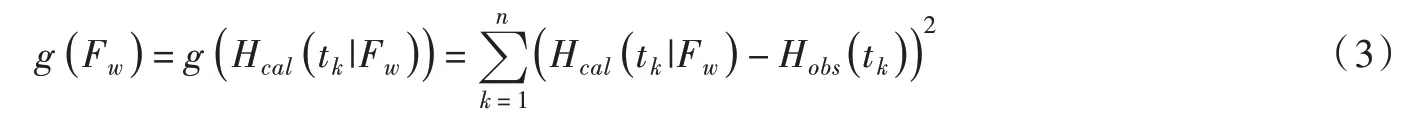
最优辨识模型

式中:g(Fw)为性能指标函数;Hcal(tk|Fw)为tk时刻热通量为Fw时计算的模拟冰厚;Hobs(tk)为tk时刻观测冰厚;n为模拟计算冰厚次数;H0为模拟计算初始冰厚值,取0.48 m;FW为冰-水界面热通量辨识范围。
不同时期冰-水界面热通量是不同的,本文将主要确定试验期间(施工前一周和施工期)的冰-水界面热通量。以雷达冰厚为观测数据,利用辨识优化方法,对冰-水界面热通量进行辨识。辨识模拟计算时间间隔tk为1 h,计算次数n=168,经过辨识优化计算,获得黄河什四份子试验期间冰-水界面热通量为9.06 W/m2。
4 冰上石笼沉排的冰力学理论和黄河关键参数确定
4.1 冰力学描述冰上石笼沉排成功与否同冰层承载力密切相关,国际上已在板壳力学的基础上发展数个冰层承载力模型,并被国内学者应用,但应用的数个冰层承载力模型主要针对瞬时载荷。无论何种冰承载力模型,都需要冰弯曲强度和弹性模量。冰温影响弯曲强度和弹性模量,冰面铺放石笼沉排后,冰内温度升高意味着冰强度随之降低。结合黄河冰晶体、密度和含泥量等物理指标[33]及冰层弯曲强度和弹性模量[34],推导出包含冰厚、冰温和衰减时间的石笼沉排下冰层承载力表达式。
(1)冰层承载力与弯曲强度、弹性模量和冰厚的隐式关系。当冰层受到半径为r的均布荷载时,冰层弯曲变形,表现为冰层上部受压下部受拉,国际上普遍采用式(5)和式(6)表示冰层承载力与弯曲强度、弹性模量、冰厚的隐式关系[19]。
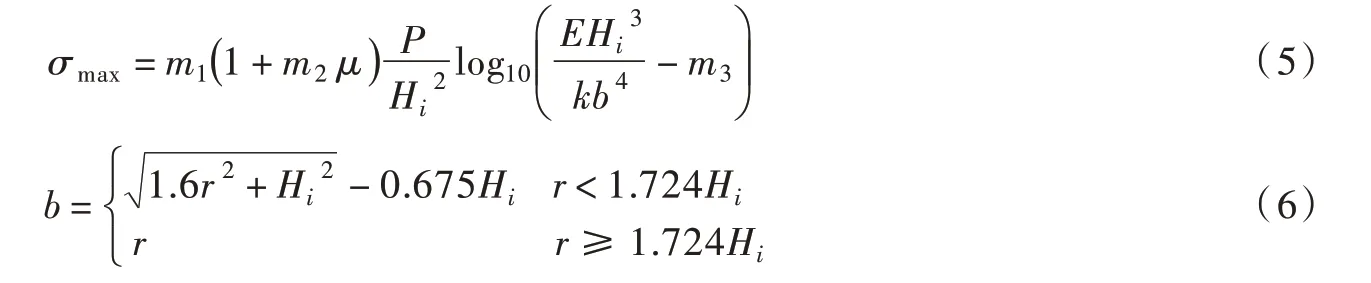
式中:σmax为最大弯曲强度,kPa;μ为泊松比,取0.3[35];P为冰层所受石笼沉排荷载,kN ;E为弹性模量,kPa;Hi为冰厚,m;k为基床反力系数,取9.8 kN/m3;r为荷载作用半径,取1.9 m;m1、m2和m3为不同加载方式的取值参数,见表2。

表2 不同荷载加载方式条件下式(5)中m1、m2和m3参数的取值
(2)冰层弯曲强度和弹性模量与冰温的关系。冰层弯曲时弯曲强度和弹性模量与冰温有关,现场试验获得黄河边乌梁素海天然冰层瞬时峰值弯曲强度和弹性模量与冰温的关系[34],见式(7)和式(8)。由于采用自然沉排,冰层承载力不得不考虑蠕变引发的长期强度。通过冰长期强度的幂函数形式[36],引入时间变量t。在式(7)和式(8)的基础上建立冰层长期载荷弯曲强度和弹性模量,见式(9)和式(10)。
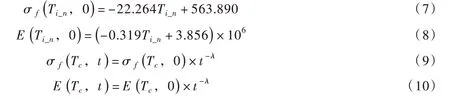
式中:σ f(Tc,t)为冰层长期弯曲强度,kPa;σ f(Ti_n,0)为冰层瞬时弯曲强度,kPa;σ f(Tc,t)为冰层瞬时等效弯曲强度,kPa;E(Tc,t)为冰层长期弹性模量,kPa;E(Ti_n,0)为瞬时弹性模量,kPa;E(Tc,0)为瞬时等效弹性模量,kPa;Ti_n为冰盖第n(n=1~20)层冰温,℃;Tc为中性轴冰温,℃;t为冰上石笼沉排单元铺放后的历时,h;λ为衰减指数。
(3)基于中性轴冰温表达的长期弯曲强度和弹性模量。石笼沉排使整个冰层失稳,只有冰层弯曲时中性轴位置的弯曲强度和弹性模量能体现整体冰层的弯曲强度和弹性模量,Kerr 和Palmer 给出确定冰层弯曲时中性轴位置的公式[37]:

式中:ℎc为中性轴距离冰表面的深度;Hi为整个冰层的厚度;E(ℎ)为冰层不同深度的弹性模量。
利用HIGHTSI 模型计算每层冰温,带入式(8)计算对应位置E(ℎ),经过式(11)迭代计算,确定ℎc。再利用ℎc所在层的冰温,带入式(7)和式(8)计算出冰层的等效弯曲强度σ f(Tc,0)和等效弹性模量E(Tc,0),之后带入式(9)和式(10)计算冰层长期弯曲强度σ f(Tc,t)和长期弹性模量E(Tc,t)。
(4)冰层失稳时刻的冰层承载力。在石笼沉排布放冰层后,冰层长期弯曲强度和长期弹性模量随着中性轴冰温和时间t变动,当t=t(b冰层失稳时刻)时,冰层出现失稳,石笼沉排开始自然下沉。将tb带入式(9)和式(10)得到冰层失稳时刻冰层长期弯曲强度σ f(Tc_b,tb)和长期弹性模量E(Tc_b,tb),钻孔实测石笼沉排区域冰厚Hi_b。
令此时的σmax=σ f(Tc_b,tb),E=E(Tc_b,tb),Hi =Hi_b,代入式(5),计算tb时冰层承载力Pb,见式(12),之后根据现场石笼沉排周边冰面变形监测结果确定tb,最后确定出冰层长期强度的衰减指数λ。
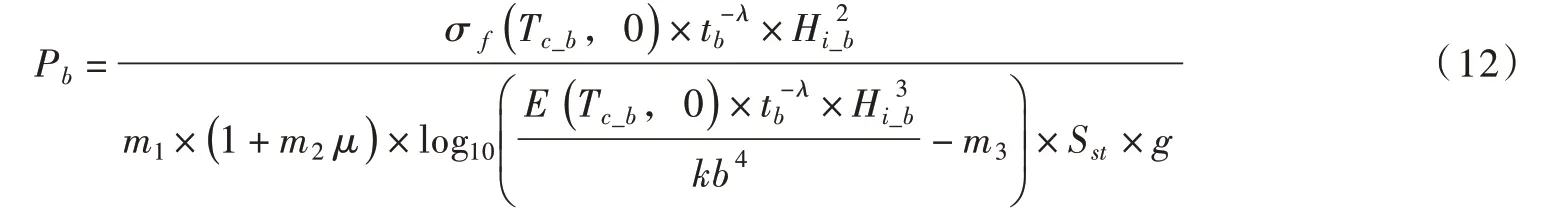
式中:tb为冰层失稳时刻,h;Tc_b为冰层失稳时刻中心轴冰温,℃;Hi_b为失稳时刻冰厚,m;Sst为石笼沉排底面积,m2;Pb为tb时刻冰层承载力,kg/m2。
4.2 冰层失稳时刻的确定试验期间5 个监测点共观测4 次冰面高程变化,分别为2021/1/24 16∶00、2021/1/25 16∶00、2021/1/26 11∶00 和2021/1/26 16∶00,获取图1(a)B 点雷达系统相同时刻监测的冰面高程数据。
为更好说明冰层在石笼沉排自重作用下的变形速率变化,去除冰面变形监测期间水位上涨影响,将监测点冰面高程变化量与同时段水位高程变化量之差作为冰面的相对变形量。以2021/1/24 16∶00作为冰面变形的起始时刻,绘制图4(a)。
从图4(a)看出,5 个监测点总体是下沉趋势,T-1 和T-5 的下沉量最大,T-1 累积下沉量0.13 m,累积下沉速率2.7×10-3m/h,T-5累积下沉量0.17 m,累积下沉速率3.5×10-3m/h,特别是2021/1/26 11∶00—16∶00 下沉量最大。对图4(a)中的T-1 和T-5 的冰面累计变形量进行拟合并计算冰层变形速率,得到图4(b)。
从图4(a)看出,随着时间增加,T-1 和T-5 累积相对变形量逐渐增大,并且存在快速增长点。图4(b)给出冰面累计变形量和变形速率随时间的关系,可以看出T-1 和T-5 处冰层出现明显变形,冰层失稳时刻为开始加载后30 h,即tb=30 h。

图4 布放石笼沉排后冰面变形监测
4.3 长期强度衰减指数的确定将布设石笼沉排试验前后2021/1/23—2021/1/28 的实测气温、湿度、风速和云量及辨识优化后的冰-水界面热通量,输入HIGHTSI 模型,计算试验期间石笼沉排下的20 层冰温。通过式(11)获得冰层弯曲时的中性轴位置,确定中性轴处冰温T(c图5)。并通过式(7)和式(8)获得冰层瞬时等效弯曲强度σ f(Tc,0)和等效弹性模量E(Tc,0)。结合试验处实测冰厚60 cm,计算天然冰层和石笼沉排下冰层承载力随时间的变化。图5 显示布放石笼沉排前中性轴位置处的冰温波动较大(-4.9~-1.6 ℃),布设石笼沉排后,则冰温先升高后下降,整体符合该时段气温先升后降的过程。
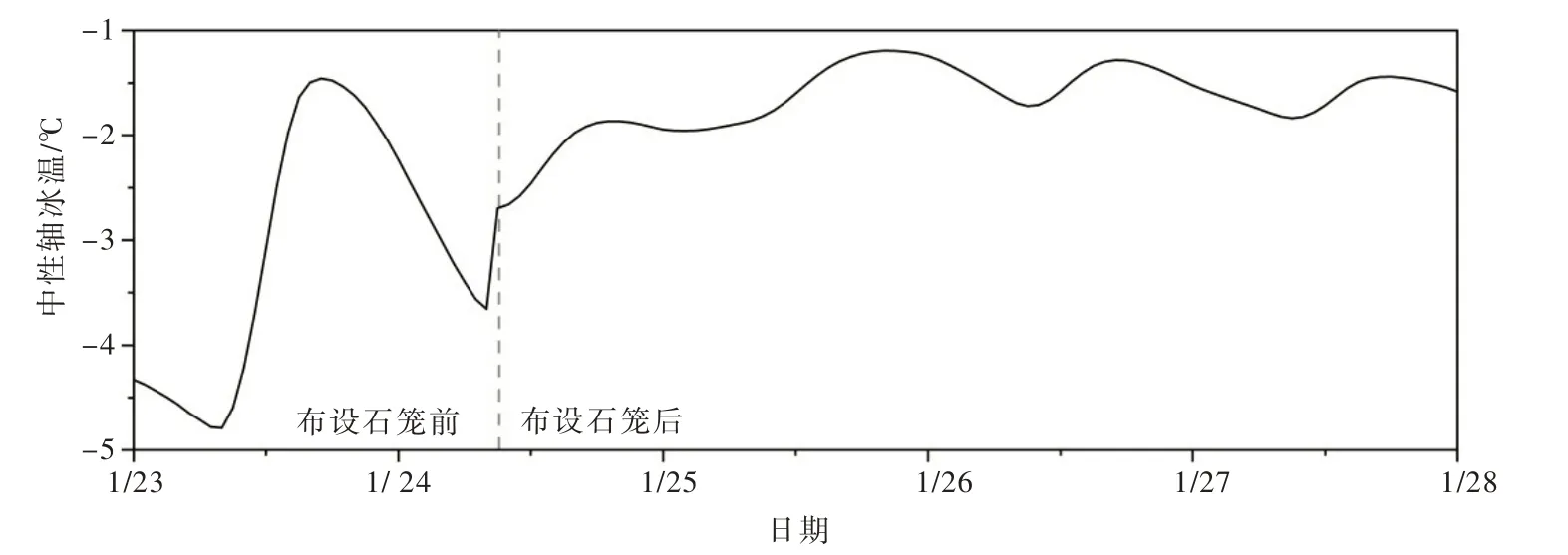
图5 2021年计算冰层承载力所需的中性轴冰温
石笼沉排加载于冰面后,结合现场实测冰厚60 cm,式(12)中冰层允许承受荷载Pb随着加载时间和中性轴冰温衰减,当Pb衰减到第1 天铺放石笼沉排失稳时刻tb=30 h 时,认为此时的Pb=1100 kg/m2(50 cm 厚的石笼沉排单位面积自重),但Pb计算式中λ值影响冰层承载力衰减速度,需要通过试算使tb=30 h 时Pb=1100 kg/m2,试算过程见图6,确定试算结果为λ=0.08。
基于确定的衰减指数λ=0.08,计算第2 天和第3 天加载石笼沉排的冰层承载力衰减过程(图7)。图7 显示第1 天和第2 天铺放石笼沉排处冰层允许承载力在第3 天前都衰减到石笼沉排单位面积自重线,即前两天铺设石笼沉排处的冰层开裂,石笼沉排淹没于水中,这与第3 天(2021/1/26 17∶00)现场观测结果一致(图8)。
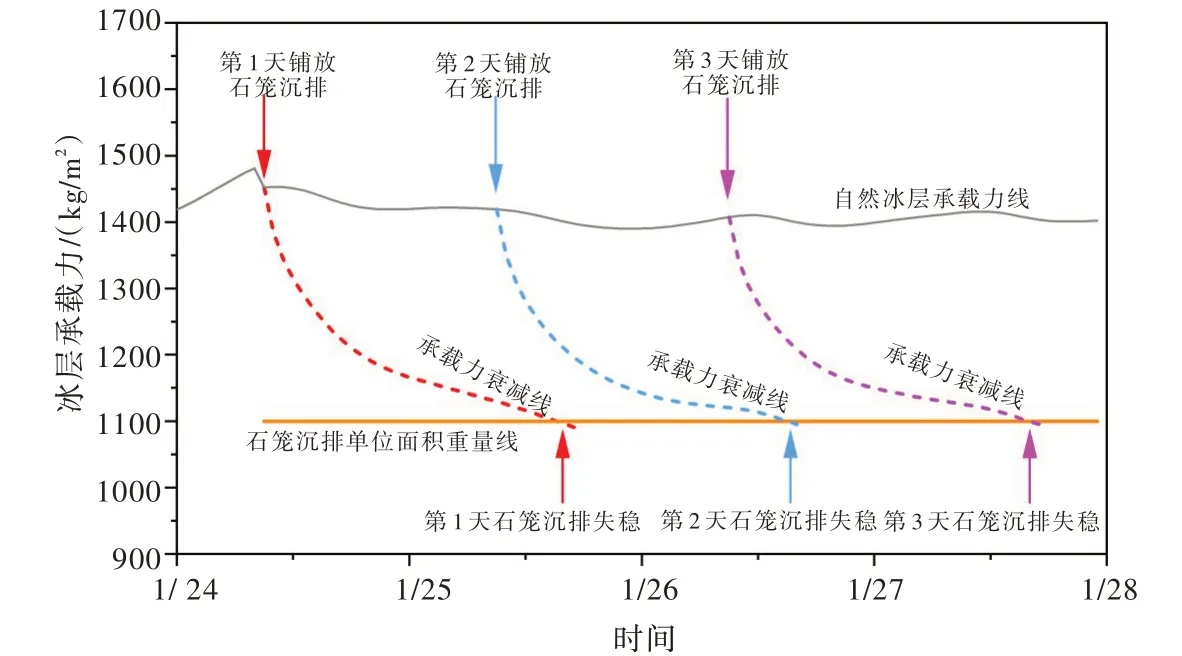
图7 试验期间自然冰层承载力和石笼沉排下冰层承载力衰减历程
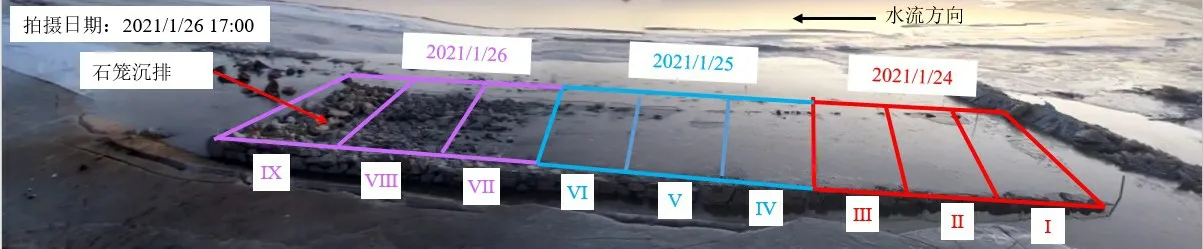
图8 2021/1/26 17∶00 冰面石笼沉排沉没状况
5 气候变暖背景下黄河冰上石笼沉排适用性分析
冰上石笼沉排利用冰层作为承载体,因此能否成功实施的关键是确认不同气温和不同冰厚组合下冰层允许承载力。在黄河宁蒙段哪些位置,哪些水文气象环境下可以实现?特别全球气候变暖的大背景下,它能否发挥作用?尽管目前黄河河冰有数个不同形式的冰生消模型[26-29],包括本文利用现场实测冰厚确定黄河冰-水界面平均热通量的一维热力学模型[30],当具体到某个河段,模型的结果难以满足工程精细要求。因此未来还需对黄河宁蒙段关键河道,典型河段开展相关现场研究,提升黄河热力、动力联合作用下的冰厚和冰温预测能力。
本节将具有不确定性的气候变化、黄河宁蒙段不同位置不确定的冰模型相关热力、动力参数等均假设为确定的。认为黄河宁蒙段同什四份子条件一致,忽略河道走向引起的辐射差异,流速差异和不同河段底泥热通量差异,即假设冰-水界面热通量9.06 W/m2和冰层长期承载力衰减系数0.08 适用于整个黄河宁蒙段,并且采用实施石笼沉排最低速度,需要5 天工作时间。按照本文方法,回答未来应用石笼沉排的需要考虑的几个问题。
目前黄河宁蒙河段沿线水文站有记载最低气温,以及多年记录的冬季风速、湿度和云量等资料,统计分析黄河宁蒙段冰上石笼沉排的环境参数范围,即冰厚30~110 cm、气温0~-30 ℃、风速5 m/s、相对湿度45%和云量20%,再利用辨识优化后HIGHTSI 模型计算各环境组合条件下冰温,利用式(12)计算石笼沉排下冰层失稳时(120 h)的承载力,加载方式为中心加载(表2),计算结果绘制图9。它是黄河宁蒙段实施冰上石笼沉排的气温和冰厚组合线。从图9 看出,随着气温降低和冰厚增加,冰面承载力越来越大。相对气温而言,冰厚对石笼沉排下冰层承载力的贡献更大。以50 cm 厚的石笼沉排单位面积重量1100 kg/m2为例,若气温为最高温度0 ℃,根据式(12)计算的无缺陷冰层条件下布放石笼沉排时施工安全冰厚至少应为66 cm,其它气温条件下施工安全冰厚见图9 中的黑色实线以上部分。
除了冰厚和冰温影响冰层承载力外,冰层内裂缝数量和深度、气泡含量、泥沙等均可视为缺陷引起承载力下降。如果冰层含有气泡、泥沙及细小裂缝(小缺陷冰层),建议对冰层中心加载方式下计算的施工安全冰厚增加10%(见图9 中黑色点划线以上部分)。如果冰层裂缝深度超过冰厚50%或者裂缝内存在水流(大缺陷冰层),这时应采用冰层边缘加载方式[8,13],它计算所得施工安全冰厚比中心加载计算的施工安全冰厚偏大32.3%~38.1%,因此建议在图9 的施工安全冰厚基础上增加40%(见图9 中黑色短划线以上部分)。
文献[38]统计了1957—2020年黄河宁蒙河段4 个水文站冰厚资料,资料显示黄河宁蒙段冰厚处于减薄趋势。它说明在全球气候变暖背景下,黄河宁蒙段冰厚会减薄。未来在黄河宁蒙段实施石笼沉排时可能遇到自然冰厚不能满足图9 计算的承载力要求,这时建议在一定条件下采取人为增加冰厚的漫灌或淋喷措施和减薄石笼沉排厚度措施。
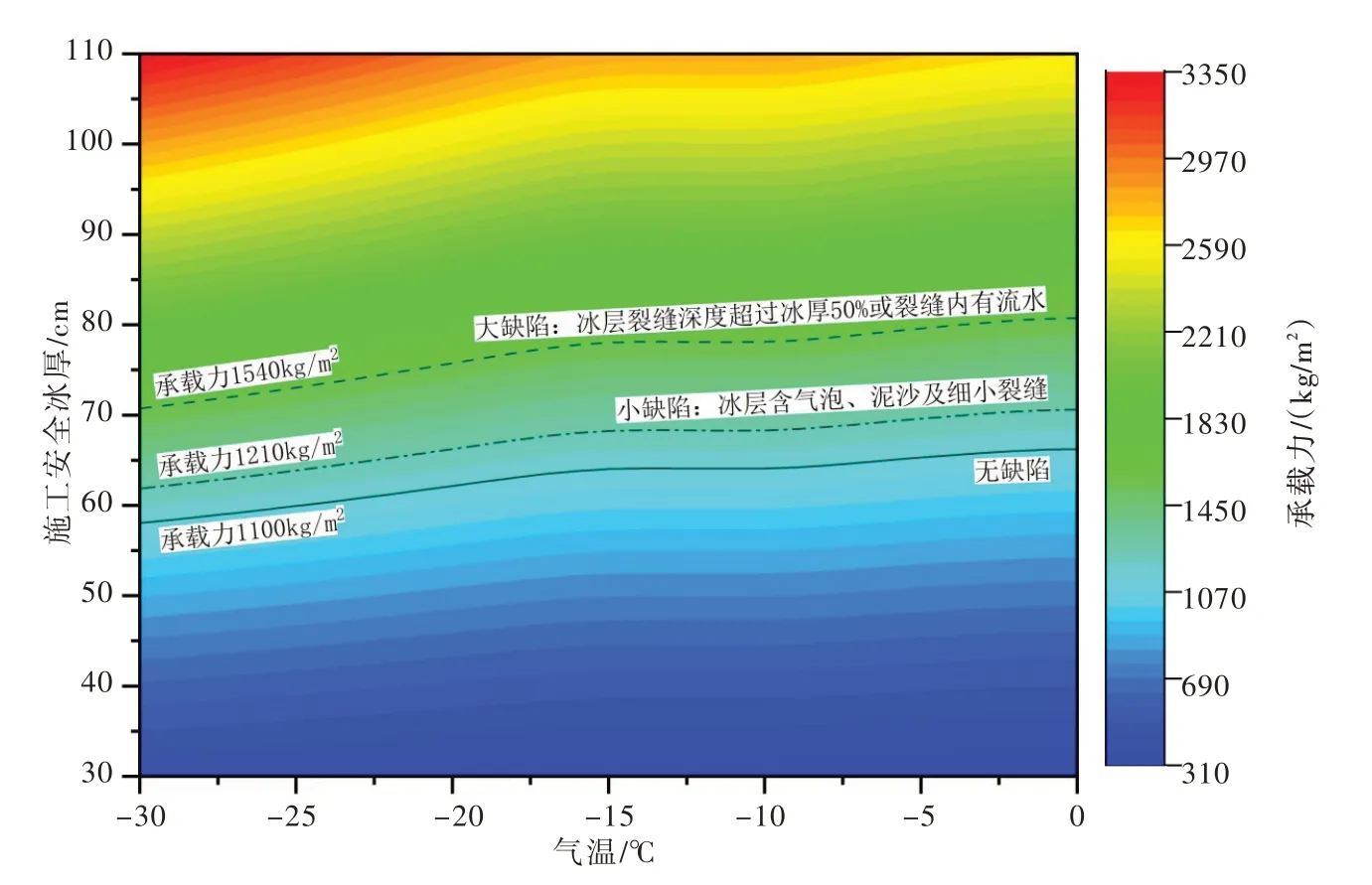
图9 不同气温与冰厚组合下冰层120h 时承载力
6 结论
本文利用冰热力学和冰力学理论知识,以及现场观测数据,对什四份子冰上石笼自然沉排试验区域冰层承载能力进行评估和分析,得出如下结论:
(1)基于HIGHTSI模型和辨识优化方法,确定出黄河什四份子试验期间冰-水界面热通量为9.06 W/m2,依据该关键参数能够计算石笼沉排下冰温剖面。利用冰层变形、冰温、冰弯曲强度和弹性模量确定什四份子石笼自然沉排长期荷载的衰减指数λ=0.08。据此,构建包含冰厚、冰温和衰减时间的冰层承载力表达式。
(2)利用构建的冰层承载力表达式,得到50 cm 厚度石笼自然沉排在无缺陷冰层条件下的气温及冰厚组合施工安全界限。如果冰层内存在气泡、泥沙和细小裂缝(小缺陷冰层),建议相同气温下施工安全冰厚增加10%。如果冰层存在裂缝深度超过冰厚50%或裂缝内有水流情况(大缺陷冰层),建议相同气温下施工安全冰厚增加40%。
(3)如果将什四份子的成果推广应用到黄河宁蒙段,目前各种黄河冰生消模式的参数化方案无法满足到具体河段的石笼自然沉排要求精度。建议未来对宁蒙段典型河段,河道开展详尽的现场调查研究。另外,未来在气候变暖条件下,可能遇到不满足承载力要求的冰厚和气温组合,建议采取增加冰层厚度(漫灌/淋喷)或者减薄石笼沉排厚度等措施。
