干湿循环作用下原状黄土宏-微观参数关系研究
2022-05-19刘禹阳来弘鹏谢门东
刘禹阳,王 耕,来弘鹏,谢门东,安 驰
(1.长安大学 建筑工程学院,陕西 西安 710064;2.长安大学 公路学院,陕西 西安 710064)
1 研究背景
黄土中含有丰富的易溶胶结物质和吸水膨胀矿物成分,其物理力学性能受水环境的影响显著。干湿循环条件下,黄土的力学性能会产生明显劣化,对实际工程建设将产生不利影响,如干湿循环劣化可能引起黄土边坡滑坡事故[1-2]。黄土具有显著的结构性[3],其宏观物理性能与微观结构特征有着密切联系,黄土微观颗粒排列特征的改变会对宏观力学性能造成重大影响。所以,全面了解黄土劣化过程中宏观力学性能的演化规律和机理,需对目标黄土开展多尺度研究,既要对黄土宏观尺度下力学性能的变化规律进行研究,也要对微观尺度下黄土颗粒联结和排列的变化机理进行分析,同时,黄土宏-微观现象跨尺度联合分析与黄土宏-微观典型参数的关系研究也十分必要。
近年来,学者们对黄土微观结构和宏观性能的关系进行了很多研究。叶万军等[4-5]通过CT 扫描试验分析了干湿循环过程中重塑黄土裂隙的演化规律及发育机理,并以此对重塑黄土宏观力学性能衰减和黄土边坡剥落的原因进行了解释;田晖等[6]通过扫描电镜试验研究了干湿循环过程中重塑新黄土微观结构的演化规律;许健等[7]通过三轴渗透试验对干湿循环过程中新黄土的渗透系数进行了分析,利用CT 扫描试验揭示了渗透系数演化规律的细观机制;潘振兴等[8]通过液塑限测定、直剪试验以及核磁共振等手段分析了干湿循环过程中多种宏观和微观参数的演化规律;袁志辉等[9-10]通过三轴试验和单轴压缩试验对压实黄土微观结构与宏观力学性能的关系进行了定性分析;郝延周等[11]发现黄土的抗剪强度与干湿循环次数和干湿循环幅度均存在非单调关系,并基于干湿循环过程中黄土微观结构的变化机理予以解释,定义了临界干湿次数和最不利干湿循环幅度;王飞等[12]对干湿循环过程中压实黄土湿陷性演化规律进行了研究并从微观尺度对其进行了解释;胡长明等[13]通过三轴试验得到了不同干湿循环次数下压实黄土的强度参数,利用扫描电镜图像对强度劣化机制进行了定性分析;李丽等[14]从微观尺度解释了盐分迁移对黄土强度和边坡稳定性的影响机理;刘博诗等[15]对不同固结度下人工湿陷性黄土的物理和力学性质进行了研究,并通过扫描电镜试验分析了微观结构参数对力学性能的影响;王铁行等[16]通过动三轴试验和扫描电镜试验获得了不同干湿循环次数下压实黄土的动强度和微观结构图像,并从微观尺度对黄土动强度劣化机制进行了解释。
可以看出,关于黄土宏观与微观尺度间的联系研究已经取得了丰厚的成果,但相关研究主要集中在黄土微观结构的演化机理和黄土宏-微观关系的定性分析方面,黄土宏观和微观典型参数定量分析需要作更深入地研究。同时,黄土干湿循环方面的研究多集中于地表新黄土或重塑黄土,而Q2原状黄土同样可能受到干湿循环作用影响,例如在地下水位升降和季节性降雨的影响下,黄土塬区隧道底部黄土围岩以及低等级公路的深路堑黄土边坡均处于干湿循环环境之中,加之地下Q2黄土的干湿赋存环境,如温度、下限含水率和含水率循环幅度等,与地表黄土差异较大,不同干湿循环条件势必产生不同的干湿劣化效应,Q2原状黄土宏-微观干湿劣化效应研究也有待开展。
本文以Q2原状老黄土为研究对象,通过三轴试验和扫描电镜试验获取干湿循环过程中原状黄土的宏观和微观土性参数,分析干湿循环过程中宏-微观土性参数的变化规律,明确不同干湿循环条件对宏微观土性参数的影响差异,最后利用宏观力学参数定义了原状黄土可变性参数,同时推导了用于描述黄土微观结构特征的孔隙特征参数,以二者作为桥梁对原状黄土宏-微观参数的函数关系进行了研究。
2 试验研究
2.1 试验材料试验土体为Q2原状黄土,取自甘肃省庆阳市宁县上阁村隧道掌子面,取土点埋深约68 m。该类黄土分布于黄土塬表层上更新统地层下部,呈棕黄色,土质均匀且较为致密。原状黄土基本物理性质指标如表1所示。

表1 Q2原状黄土基本物理性质指标
2.2 试验方案本次研究首先将Q2原状黄土削制为39.1 mm × 80 mm 的三轴试样,之后对其进行干湿循环试验,在达到规定干湿循环次数后,开展三轴压缩及扫描电镜试验,获得不同干湿循环次数下原状黄土的宏观力学参数和微观结构参数。
(1)干湿循环试验。根据隧道地勘资料,相近埋深黄土的天然含水率总体在17% ~19%之间,饱和含水率为26%,为方便分析和区别循环参数的影响,试验将18%和26%定为关键含水率,以干湿循环幅度和下限含水率为划分标准,三种干湿循环工况设置为:工况1 为含水率10% ~18%循环、工况2 为含水率10% ~26%循环、工况3 为含水率18% ~26%循环,其中,工况1 与工况2 下限含水率相同循环幅度不同,工况1 与工况3 循环幅度相同下限含水率不同。工况3 可以反映试验黄土在天然条件下的性能劣化情况,分别对比工况1 与工况2、工况1 与工况3 试验结果,可得到不同循环幅度和不同下限含水率对黄土劣化规律的影响。
取样点为隧道洞周黄土2 m 深处,地层温度在17 ~20 ℃之间,试件干燥过程中烘箱温度设定为20 ℃。由于黄土试样干密度已知,在确定目标含水率后,可换算得到相对应的试样目标质量,烘干过程中,通过监测试样质量变化,可实现目标含水率的控制。在众多黄土干湿循环研究中[3-14],黄土的干湿循环次数为3 ~12 次不等,黄土的劣化程度与干湿循环次数正相关。对于Q2原状黄土,其颗粒排列紧密,对干湿循环作用的抵抗能力较强,因此,为了使试验土体在干湿循环过程中充分劣化,本试验分别对3 种工况下的原状黄土试样进行12 次干湿循环,并在第1、3、6、9、12 次循环后进行三轴压缩和扫描电镜试验。
(2)三轴剪切试验。研究通过GDS 静态三轴仪进行三轴固结不排水剪切试验,采用应变控制,根据《土工试验方法标准》(GB/T 50123-2019),剪切速率设为0.08 mm/min。分别对不同工况和干湿循环次数下的原状黄土试样重复进行3次剪切试验,用以确定不同循环条件下黄土的抗剪强度、黏聚力和内摩擦角,测试含水率为各工况的干湿循环下限含水率,即工况1和工况2为10%,工况3为18%。受开挖卸荷作用影响,深埋黄土隧道围岩压力一般在100 ~500 kPa左右,本次试验围压σ3分别取100、200、300 kPa。
(3)扫描电镜试验。采用JSM-6460LV 型低高真空数字化电子显微镜进行扫描电镜试验,基于不同工况和干湿循环次数下原状黄土的微观图像,直观观测土颗粒与孔隙的形态和结构特征,定性分析黄土微观结构的演化规律,通过ipp 软件进行图像处理定量获取黄土微观结构参数。为确保清晰观测到黄土颗粒和孔隙的微观结构,试验中微观图像的放大倍数取为1000 倍。孔隙面积比F为孔隙总面积AV和图像总面积A0的比值,用于衡量黄土中的孔隙含量,孔隙面积比越大则孔隙含量越高;孔隙分形维数D可以反映黄土中孔隙结构的复杂程度,分形维数越大则孔隙分布越复杂,孔隙集中度越高,计算公式见下。

式中:F为孔隙面积比;D为孔隙分形维数;AV为孔隙总面积;A0为图像总面积;L为孔隙等效周长;A为单个孔隙面积;C为常数。AV、A0、L和A可由图像处理直接得到。
2.3 试验结果及分析
(1)宏观和微观土性参数定量分析。不同干湿循环工况下原状黄土峰值偏应力随循环次数的变化曲线如图1 所示。随着干湿循环次数的增加,原状黄土试样的峰值偏应力持续降低,同一工况不同围压下,峰值偏应力变化曲线整体相似(图1(a))。工况2 条件下,原状黄土峰值偏应力衰减量最大且速度最快,特别是循环3 次后,工况2 峰值偏应力衰减量远大于其他工况,工况3 和工况1 条件下黄土峰值偏应力变化量除第3 次循环时偏差较大外,其他循环整体变化量较为接近(图1(b))。
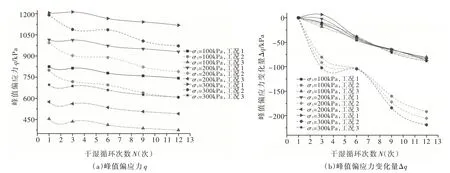
图1 原状黄土峰值偏应力与干湿循环次数的关系曲线
不同工况原状黄土宏观力学参数随干湿循环次数变化曲线如图2 所示。随着干湿循环次数的增加,3 种工况下原状黄土试样的黏聚力均持续降低,工况2 条件下黏聚力衰减最快且衰减值最大,12次循环后降低48.9 kPa,衰减率达到27.9%,工况3 黏聚力衰减速度与衰减值低于工况2,12 次循环后降低24.6 kPa,衰减率22.0%,工况1 黏聚力衰减最慢且衰减值最小,降低22.4 kPa,衰减率12.1%(图2(a))。干湿循环过程中,3 种工况下原状黄土内摩擦角变化幅度始终较小,工况2 条件下变化幅度最大但仍仅有1°(图2(b))。
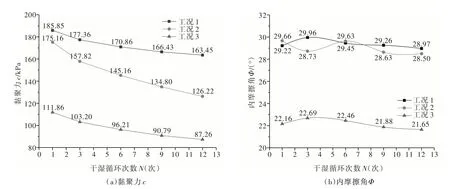
图2 原状黄土宏观力学参数与干湿循环次数的关系曲线
图3 为不同工况黄土微观结构参数随干湿循环次数变化曲线。如图所示,随着干湿循环次数的增加,各工况孔隙面积比基本呈线性显著增加,工况2 条件下孔隙面积比的增长速度最快且量值最大,量值增加0.14,工况3次之,量值增加0.08,工况1增长最慢且最小,增加0.03(图3(a));12次干湿循环过程中,3种工况下原状黄土的孔隙分形维数均呈非单调缓慢增大,但整体变化不大,工况2 条件下黄土孔隙分形维数增长速度最快,增加0.15,工况3 次之,增加0.06,工况1 最慢,增加0.04(图3(b))。
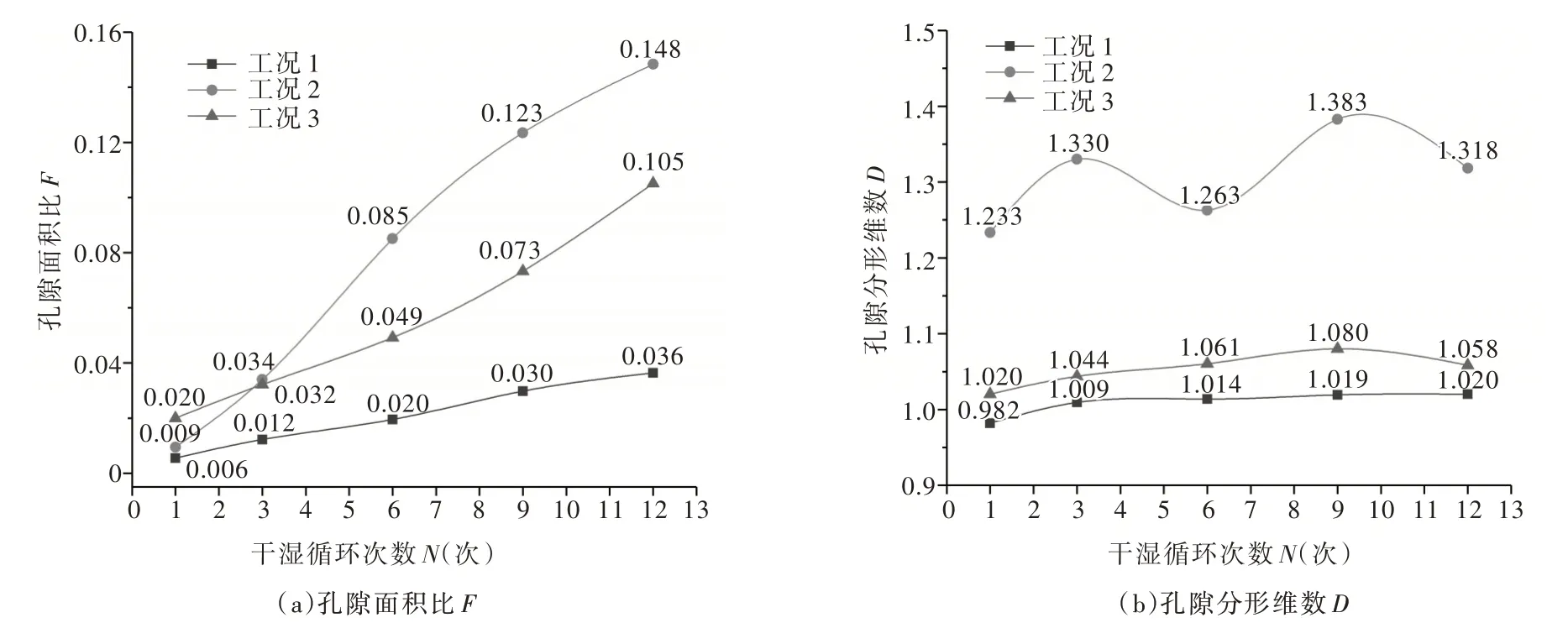
图3 原状黄土微观结构参数与干湿循环次数的关系曲线
综上所述,3 种干湿循环工况对原状黄土的劣化影响效果明显不同且存在较为相同的规律。工况2 的干湿循环条件下,原状黄土试样劣化效果最显著,宏观强度参数和微观结构参数的变化速度最快(图2(a)、图3(a)(b)),工况3 整体次之,工况1 整体最小。对比3 种工况发现,工况1 和工况2 的下限含水率相同,但工况2 的干湿循环幅度更大;工况1 和工况3 的干湿循环幅度相同,但工况3 的下限含水率更高。因此,干湿循环幅度越大,下限含水率越高,则干湿循环对黄土的劣化影响越显著,黄土内部孔隙含量和集中度的增长速度越快,黏聚力和抗剪强度的衰减速度也越快。另外,工况3 的测试含水率远大于工况1 和工况2,较高的含水率使得黄土颗粒间的原始黏聚力和固化黏聚力降低,滑动摩擦与咬合摩擦变弱。因此,从量值上来看,工况3 中原状黄土的峰值偏应力、黏聚力和内摩擦角均小于另外两种工况(图1(a)、图2(a)(b))。
(2)电镜图像定性分析。利用微观图像直接观测黄土颗粒和孔隙的微观结构,对不同循环条件下的黄土微观结构变化特征进行定性分析,限于篇幅,仅展示工况2 中第1 次和第12 次干湿循环后黄土试样微观结构图像,如图4 所示。1 次干湿循环条件下,黄土结构较为紧密,土颗粒间以嵌固排列和面接触为主,孔隙含量相对较低,如图4(a)。12 次干湿循环后,黄土微观结构逐渐松散,大量中、大孔隙存在,黄土结构较为薄弱位置有孔隙贯通形成微观裂隙,孔隙发育处黄土颗粒间的连接方式转变为架空排列和点接触,如图4(b)。究其原因为干湿循环过程中,黄土颗粒间的胶结物质反复溶解迁移,使得颗粒间的联结强度持续降低,部分矿物在干湿循环过程中不断膨胀或收缩,导致颗粒间的联结作用在不均匀的拉应力下发生破坏,颗粒较大的集粒逐渐破碎,土颗粒间趋向于离散。

图4 工况2 干湿循环中原状黄土微观图像
由上述宏微观结果分析可知,干湿循环过程中,原状黄土表现出了明显的劣化特征,土颗粒间稳定的面接触和嵌固排列逐渐转变为不稳定的点接触和架空排列(图4(a)(b)),黄土结构变得松散。随着循环次数的增加,原状黄土孔隙结构持续发育,孔隙含量不断增长(图3(a)),同时由于原状黄土内部孔隙分布不均匀[17],孔隙的扩张过程主要集中在孔隙较多的脆弱部位,因此孔隙的集中度也呈现增长趋势(图3(b))。随着黄土孔隙结构的不断扩张,黄土颗粒间的距离逐渐增大,使得颗粒间的吸引力不断降低,与此同时,黄土中普遍存在的胶结物质在干湿循环作用下反复溶解迁移,使得颗粒间的胶结力持续衰减,导致黄土黏聚力在干湿循环过程中不断减小(图2(a))。然而,黄土颗粒间的咬合摩擦作用受干湿循环影响并不显著,黄土内摩擦角变化幅度较小(图2(b))。原状黄土峰值偏应力反映黄土抗剪强度,受黏聚力和内摩擦角影响,呈现出持续减小的变化规律(图1(a))。
3 原状黄土宏-微观参数关系研究
大量研究表明,土体微观结构特征的改变会对宏观力学性能产生重大影响,二者之间有着千丝万缕的联系。为定量研究原状黄土宏观和微观参数间的数量关系,分别定义黄土可变性参数和孔隙特征参数表达式,将二者作为桥梁用以研究原状老黄土宏-微观参数的函数关系。
3.1 基于宏观力学参数的原状黄土可变性参数
3.1.1 原状老黄土可变性参数表达式 综合结构势思想首先由谢定义等[18]提出,众多专家学者在其基础上进行了深入的研究并取得了丰硕的成果。综合结构势思想认为土体的结构性是联结和排列两方面的综合反映,结构的联结特征和排列特征分别称为结构的可稳性和可变性。结构性参数定义为m1与m2的比值[19],其中m1反映土体的可变性,m1越大则可变性越大,m2反映土体的可稳性,m2越小则可稳性越大,即土体结构性的大小由可变性与可稳性的乘积决定。黄土的结构性与其宏观力学性能有着密切联系[17],原状黄土在压剪作用下的抗力构成主要表现为胶结产生的抗力、水膜吸力作用产生的抗力以及嵌固摩擦作用产生的抗力三部分,而黄土可变性和可稳性的丧失会分别使三者所表现出的结构势释放,导致黄土抗剪强度衰减,即可以认为黄土的抗剪强度源于黄土的结构性,结构性越强,则在结构破坏前黄土的抗剪强度就越强。
基于以上观点,本文将原状黄土的可稳性和可变性视为黄土宏观抗剪强度的贡献者,二者的乘积决定了原状黄土抗剪强度的大小,可变性越大,则黄土抗剪强度中可变性的贡献比例就越大,可稳性亦然。将黄土抗剪强度与可稳性的比值定义为黄土可变性参数m,用以反映黄土的可变性,m越大则可变性越大,反之则越小。对于原状黄土抗剪强度,本文用三轴试验下原状黄土试样的峰值偏应力q表示;对于黄土的可稳性,其来源于所有土粒间的结合力[20],在宏观尺度下即为黏聚力c和内摩擦角φ的综合反映,与c+tanφ成正比,由于干湿循环过程中黄土内摩擦角φ变化幅度很小(图2(b)),因此本文用黏聚力c表示原状黄土的可稳性。则原状黄土的可变性参数m可由式(3)表示:

式中:q为原状黄土峰值偏应力;c为原状黄土的黏聚力。
3.1.2 干湿循环条件下原状黄土可变性参数变化规律 利用试验所获得的数据计算各工况下原状黄土可变性参数m,σ3=100 kPa时可变性参数变化曲线如图5 所示。由图可知,在干湿循环过程中,原状黄土可变性参数m总体呈现增长趋势,其中,工况2 条件下m的增长速度最快,工况3 次之,工况1 最慢。可以看出,对于原状老黄土而言,干湿循环作用会增大可变性对黄土抗剪强度的贡献比例;干湿循环作用的影响能力越强,则干湿循环对黄土可变性的增大效果越显著;土体可变性大小取决于结构破坏时所造成的宏观强度损失量[21],即为不稳定结构的承载能力,受测试含水率影响显著,虽然工况3条件下黄土可变性的增长速度快于工况1,但由于其测试含水率远大于另外两种工况,因此工况3条件下土体可变性对黄土抗剪强度的贡献比例最低。另外,在3种工况下,原状黄土可变性参数的变化规律均表现出了非单调性,这是由于黄土内部结构的破坏和新结构的产生所导致的。
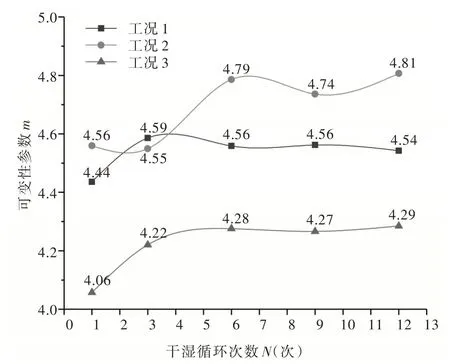
图5 可变性参数的变化曲线
3.2 原状黄土可变性参数与孔隙特征参数关系研究
3.2.1 原状老黄土孔隙特征参数 黄土内部结构的稳定性和承载力受孔隙含量及分布情况影响显著[22],孔隙结构的发育程度越高,则黄土颗粒排列越松散,架空排列结构越多,结构承载能力越弱。而对于黄土的可变性,其反映的是黄土内部结构的承载能力。因此可以看出,原状黄土的可变性与孔隙结构特征是存在联系的。
在黄土的微观结构参数中,孔隙面积比F可用于衡量黄土中的孔隙含量,孔隙分形维数D可以反映黄土中孔隙结构的复杂程度,本次研究将孔隙面积比F与孔隙分形维数D的乘积F·D定义为孔隙特征参数K,孔隙特征参数K越大,则表示黄土微观孔隙结构发育程度越高,颗粒的排列结构越不稳定,如下式所示。

利用试验所获得的数据计算不同工况下的孔隙特征参数K,绘制曲线如图6 所示,在干湿循环过程中,原状黄土的孔隙特征参数在3 种工况下均单调增长,其中工况2 条件下孔隙特征参数增长速率最快,工况3 次之,工况1 最慢。可以看出,对于原状老黄土而言,干湿循环影响能力和干湿循环次数的增长均会导致土体内部孔隙结构发育,结构稳定性降低。同时,3 种工况下孔隙特征参数的变化规律和大小关系与黄土孔隙含量(图3(a))一致,说明孔隙特征参数K可以正确反映黄土的微观孔隙结构特征。
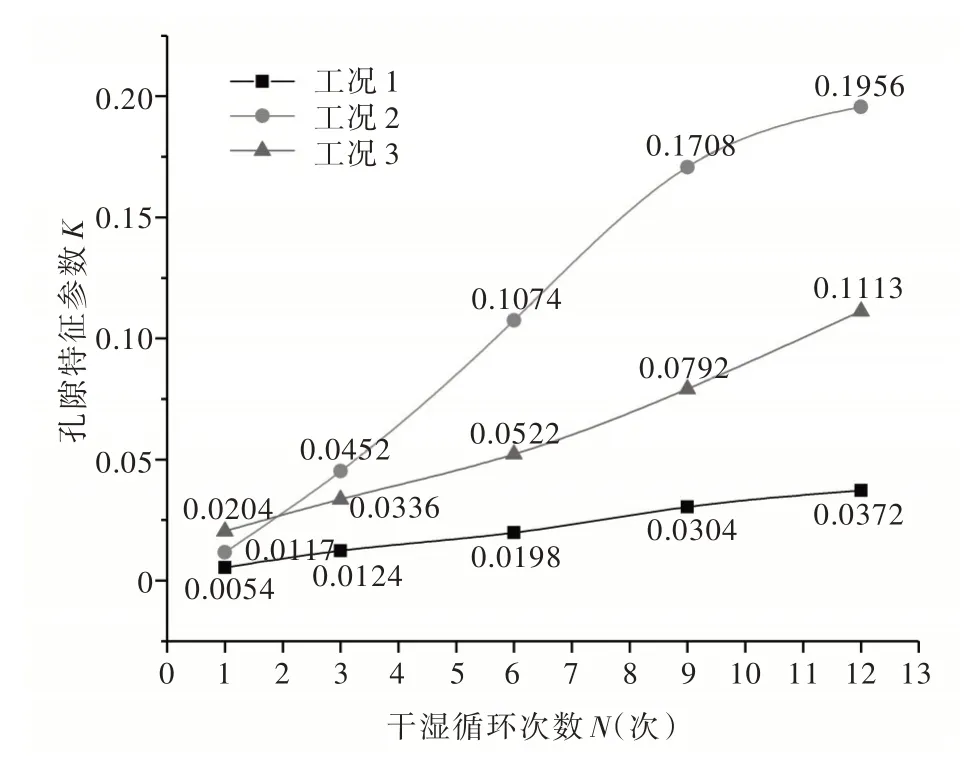
图6 孔隙特征参数的变化曲线
3.2.2 原状黄土可变性参数随孔隙特征参数的变化规律 为研究原状黄土可变性参数与孔隙特征参数的变化规律,绘制3 种工况下黄土可变性参数m与孔隙特征参数K的关系图像如图7 所示,随原状黄土孔隙特征参数的增大,3 种工况下黄土可变性参数的变化规律均表现出了非单调性,可变性参数总体而言均有所增长,二者的变化规律与三角函数接近。可以看出,对于原状老黄土而言,黄土内部孔隙含量和分布情况的改变会对微观结构的承载能力产生重大影响,进而导致黄土可变性产生变化。但是,黄土可变性参数随孔隙特征参数的变化规律是非单调的,即孔隙特征参数并非是决定黄土可变性的唯一因素。
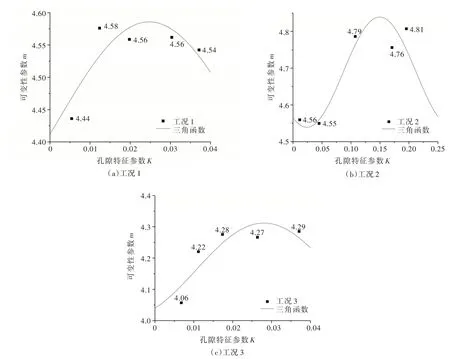
图7 原状老黄土可变性参数与孔隙特征参数的关系图像
3.3 原状黄土宏-微观参数的函数关系黄土的可变性参数由峰值偏应力q与黏聚力c的比值得到,孔隙特征参数由孔隙面积比F和孔隙分形维数D的乘积得到,上文定性分析了原状黄土可变性参数随孔隙特征参数的变化规律,发现二者间存在联系,即表明上述4 个宏观和微观参数间存在联系。但是,可变性参数与孔隙特征参数的变化曲线比较复杂,想要以此定量描述黄土宏观和微观参数间的关系是很困难的。为研究原状黄土宏-微观参数的函数关系,以黄土黏聚力c作为横坐标,峰值偏应力与孔隙特征参数的比值q/K作为纵坐标,绘制二者的变化曲线如图8 所示。
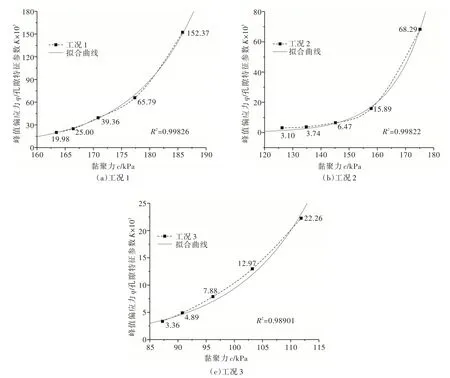
图8 原状老黄土峰值偏应力与孔隙特征参数的比值和黏聚力的关系曲线
由图可知,随着黄土黏聚力的增大,3 种工况下峰值偏应力与孔隙特征参数的比值均单调增加,且二者的变化规律均服从指数函数关系,拟合曲线如图8 所示,由此得到原状黄土宏-微观参数的函数关系如式(5)所示:

式中B1、B2为拟合参量。
可以看出,在3 种工况中,式(5)均取得了良好拟合效果,拟合度均大于0.9,且图形较为简单,仅含有两个拟合参量,易于描述黄土各项宏观和微观参数间的数量关系。为研究式(5)的物理意义,参考原状黄土可变性参数m,将原状黄土抗剪强度视为黏聚力和孔隙特征参数的贡献量之和,用q/K来衡量黏聚力c对原状黄土抗剪强度的贡献比例。随着原状黄土黏聚力的增加,一方面,颗粒间的联结强度增大,黄土可稳性对抗剪强度的贡献增加;另一方面,黏聚力的增大使颗粒排列结构的稳定性和承载力增强,可变性对黄土抗剪强度的贡献增加,两方面共同作用下,黏聚力的贡献量在黄土抗剪强度中的占比呈指数增长。
为验证上述黄土宏-微观参数函数关系式的合理性,利用Jian Xu 等[23]的原状黄土试验数据进行验证。文献中试验土体为Q3原状黄土,干湿循环下限含水率为小于1%的绝对干燥条件,干湿循环上限含水率和三轴试验测试含水率均为20%,文中以试样不同初始含盐量将干湿循环工况划分为4 种,初始含盐量分别为0.0%、0.5%、1.0%和1.5%。文献中相关试验数据,以及孔隙特征参数K和峰值偏应力与孔隙特征参数比值q/K计算结果如表2所示,峰值偏应力与孔隙特征参数的比值q/K和黏聚力c的拟合曲线如图9 所示。由图可知,文献4 种工况下,试验数据均服从式(5)分布,拟合度均大于0.9,说明利用式(5)来分析解释黄土宏观和微观参数的函数关系是较为合理的。

图9 4 种工况下原状黄土峰值偏应力与孔隙特征参数的比值和黏聚力的关系曲线
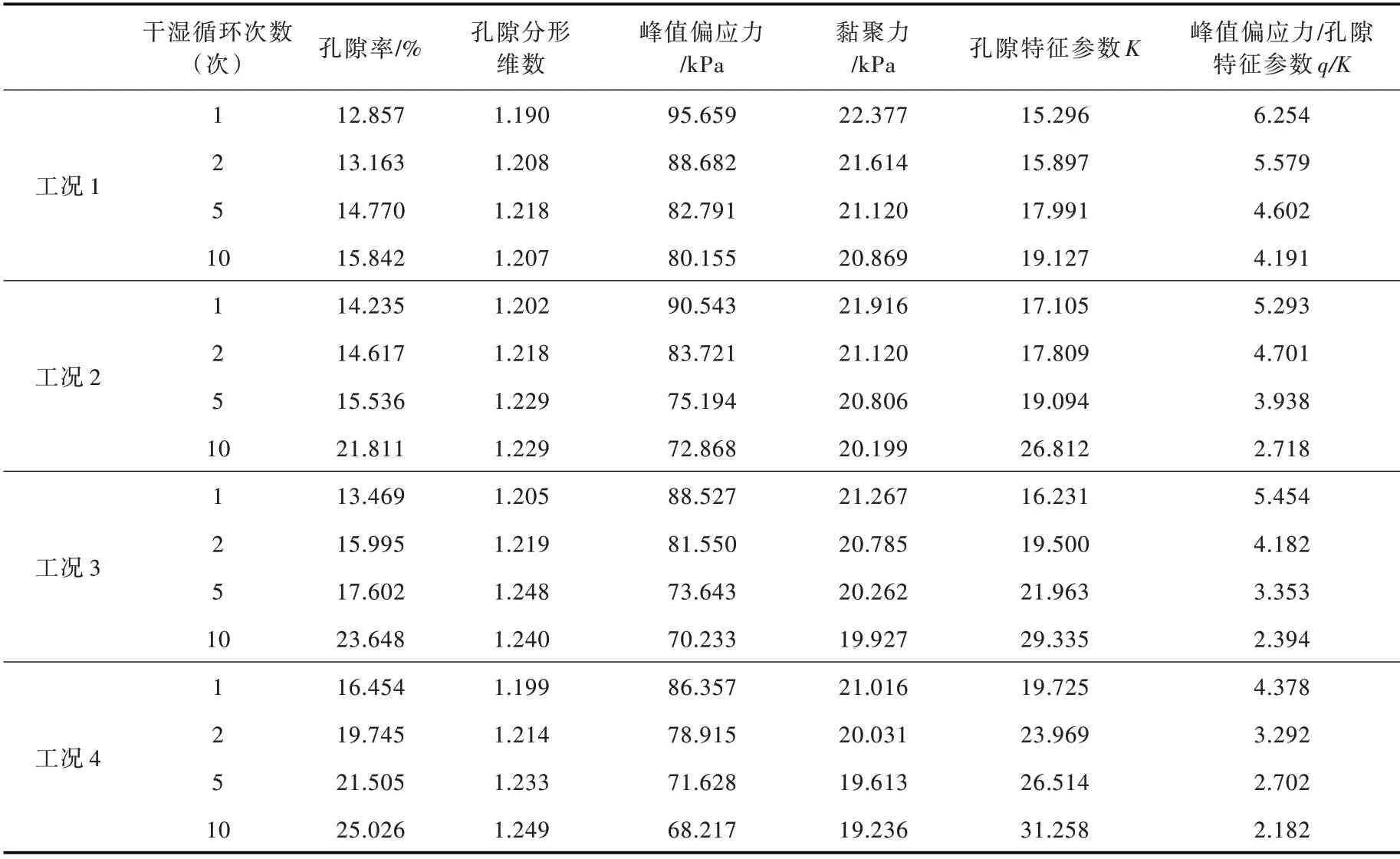
表2 不同循环工况下原状黄土试验数据[23]及计算结果
4 讨论
由上文可知,随着原状黄土内部孔隙含量和集中度的增大,黄土可变性参数m呈现出非单调变化规律(图7)。现对干湿循环过程中黄土可变性的变化机理作进一步讨论。
黄土的可变性是黄土内部不稳定结构承载能力的反映,在结构未发生破坏时,其本身可以承受部分荷载,增强黄土的抗剪强度,而在结构发生破坏后,其承载能力将会丧失,导致黄土强度降低。黄土可变性的大小并不仅仅取决于孔隙特征参数,同时与黄土的黏聚力也有着密切联系。在干湿循环过程中,原状黄土孔隙特征参数和黏聚力的变化规律示意图如图10 所示,黄土的孔隙含量随循环次数的增加而不断增大(图3(a)),且孔隙集中度增加(图3(b)),而黄土的黏聚力却随着循环次数的增加而不断减小(图2(a))。当黄土中的孔隙发育程度很低时,土颗粒间以面接触和嵌固排列为主,内部架空结构较少且均为稳定结构,这些结构由于变形空间的限制而难以发生破坏。所以,即使黄土黏聚力较大,结构承载能力强,黄土的可变性实际上并不大;而当黄土中的孔隙发育程度很高时,土颗粒间存在大量点接触和架空排列,结构很容易发生破坏,但由于黄土黏聚力低,颗粒间联结强度弱,故结构的承载力不高,黄土可变性也不大。可以看出,在黏聚力和孔隙发育程度处于极大或者极小的情况下,黄土的可变性均不大,反而是在黏聚力和孔隙发育程度均处于大小适中的状态时,黄土内既存在充足的不稳定结构,颗粒间也有足以维持结构稳定承载的联结力,黄土的可变性也较大。
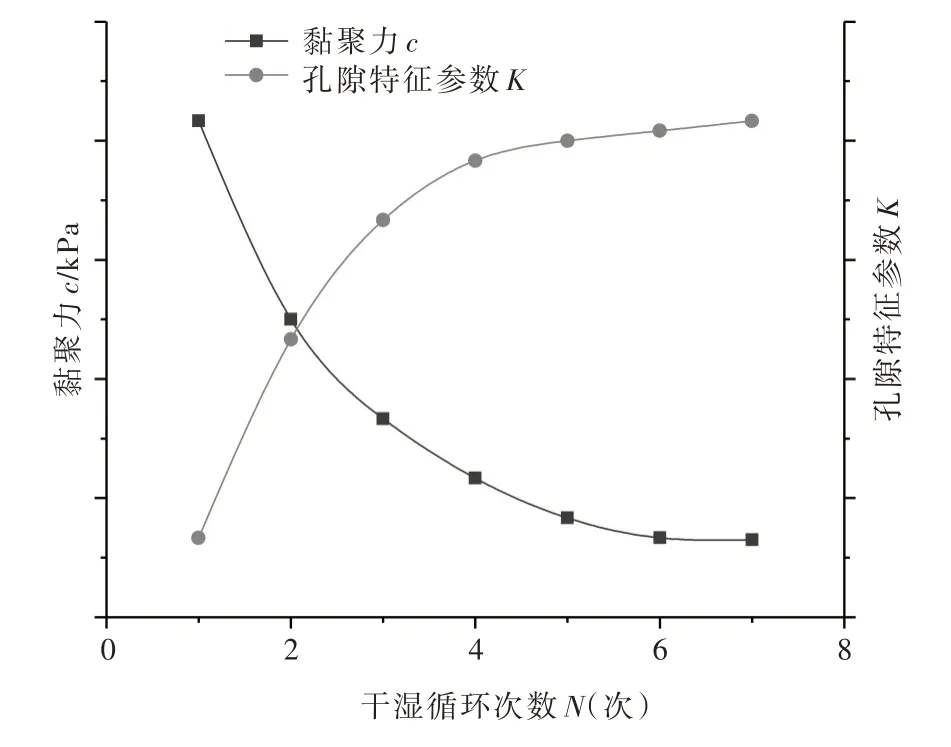
图10 黄土黏聚力和孔隙特征参数变化规律示意
对于结构密实的原状老黄土,在初始状态下,其内部多为稳定结构,黄土可变性较低。随着干湿循环次数的增加,原状黄土内部的不稳定结构开始增多,黄土可变性有所增大。之后由于不稳定结构的承载力持续降低,黄土可变性又会有所减小。因此干湿循环过程中,原状老黄土的可变性参数会呈现出先增大后减小的变化规律,考虑到黄土原生结构的破坏和次生结构的产生过程,可变性参数的增大和减小过程会不断重复发生,其变化曲线的波动现象(图5)可以得到解释。
5 结论
本文通过三轴压缩试验和扫描电镜试验对不同干湿循环条件下原状黄土的宏观和微观参数进行研究,基于综合结构势思想定义了黄土可变性参数,推导了孔隙特征参数表达式,并通过研究二者的数量关系,构建了原状黄土宏-微观参数的函数关系式,得到结论如下:(1)在同一工况下,随着干湿循环次数的增加,原状黄土孔隙含量不断增大,孔隙集中度增加,黏聚力逐渐降低,抗剪强度持续劣化,但内摩擦角变化幅度较小;干湿循环幅度越大,下限含水率越高,干湿循环对原状黄土的劣化影响越强,宏观力学性能的衰减和孔隙结构的扩张越快。(2)干湿循环过程中,原状黄土可变性对抗剪强度的贡献比例有所增大;干湿循环幅度越大,下限含水率越高,干湿循环作用对黄土可变性的增强效果越显著;随着干湿循环次数的增加,原状黄土内部原生结构逐渐破坏,次生结构逐渐产生,黄土可变性参数的变化规律表现出非单调特征。(3)原状黄土可变性受孔隙发育程度影响显著,可变性参数m随孔隙特征参数K非单调变化。随孔隙特征参数K的增大,原状黄土可变性参数m整体呈增长趋势变化,二者的变化规律与三角函数接近。(4)随着原状黄土黏聚力的增大,一方面,颗粒间的联结强度增大,可稳性对黄土抗剪强度的贡献增加;另一方面,颗粒排列结构的承载力增大,可变性对黄土抗剪强度的贡献增加,两者共同作用下,黄土峰值偏应力与孔隙特征参数的比值q/K随黏聚力c的变化规律服从指数函数关系。
