水幕隔尘用缝隙喷口的边界流线构造与出流速度分布*
2022-05-19温智超王海桥陈世强蒋加川
温智超,王海桥,2,陈世强,2,刘 宇,蒋加川,吴 朋
(1.湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201;2.湖南省矿山通风与除尘装备工程技术研究中心,湖南 湘潭 411100;3.深圳市中金岭南有色金属股份有限公司 凡口铅锌矿, 广东 韶关 512300)
0 引言
水幕除尘是湿式除尘技术的一种具体实施方式[1-2],采用通风和净化水幕的方式,将含尘气流与连续液膜或喷雾式水幕混合而达到气流净化效果,主要涉及惯性碰撞、接触阻流等除尘机理,一般可实现水膜、水滴、水雾3级除尘,除尘效率高[3-4]。同时,传统的连续液膜式水幕会阻隔巷道或隧道,喷雾式水幕在较大风量、烟尘粒径大等复杂工况下对烟尘的阻隔能力并不理想。因此,研究新型除尘装置对降尘作业尤为重要。
对于连续液膜式水幕,国内外学者主要对水幕安装位置、除尘系统结构等影响水幕除尘效率的因素展开研究:吴慧英等[5]研制悬浮水幕式除尘器,从根本上解决了管道、喷嘴堵塞的问题;熊建军等[6]围绕自激式除尘器,借助微压检测技术获得除尘腔体内的负压分布规律;张巍等[7]和贾彬彬等[8]先后确立风量、节流装置开度、除尘效率和全压损失之间的量化关系,指导工程优化。采用纱网辅助形成水膜可解决自激式阻力大等应用问题,但是为了使粉尘和水膜能够进行持续惯性碰撞,需要足够的供水量。针对井下巷道粉尘污染,田晓红等[9]研制水幕除尘装置,该装置利用除尘液在纱网上小孔形成水膜而吸附气流中的粉尘,实现污风净化。针对单道或多道防尘水幕帘在实际应用中除尘效率低于预期的问题,丁尧等[10]改进纱网喷嘴布置方式,研制全断面双层水幕帘,显著提升巷道内的抑尘率。但类似于一种水幕除尘装置的纱网辅助水幕除尘,会阻隔巷道或者隧道影响作业。喷雾式水幕相比液膜式极大地增加与周围气体进行动量、热量交换的表面积,具有良好的隔烟降温性能,因此国内外学者对其研究集中于隧道火灾治理技术领域中。根据相似性原理按比例搭建实验平台并建立数值模拟模型, Reiko等[11]发现水幕对高温和烟尘具有较好的隔断效果;Makot等[12]研究热烟对水幕隔断效果的影响,发现水幕的隔断效果和防火门与防火百叶窗类似;Blanchard等[13]对隧道中水雾、热烟的相互作用进行研究,发现细水雾具有很强的吸热作用,但是小雾滴在离开喷嘴后会迅速减速; Jiayun等[14]发现在较强的纵向通风条件下,烟气会从小雾滴间的孔隙中逸出,喷雾式水幕对烟气阻隔的有效性降低。大量研究表明,喷雾式水幕仅在较小通风条件下具有良好的隔烟降温效果。
缝隙喷口和箱式水幕可以形成宽薄水幕,常用于轧钢冷却和地下建筑防火隔烟[15-16],但箱式水幕体积较大并且喷出的水幕不均匀,因此提出1种利用缝隙喷口直接形成连续液膜式水幕用于隔尘以及除尘的方法,其优点在于不会对巷道或者隧道形成阻隔;水幕主体为连续液膜,对含尘气流形成阻隔,液膜底部破碎形成的水滴和水雾,可以捕捉气流中的尘粒,达到降尘效果。但目前常规锥形缝隙喷口形成的水幕存在出流速度不均、水膜破碎快的问题。
因此,在前人研究基础上,本文基于边界流线构造提出流线型边界线,建立流线型缝隙喷口的三维物理模型,采用流体动力学技术,比较分析不同缝隙喷口的内部流场,以得到更好的缝隙喷口边界流线结构,为隔尘水幕用缝隙喷口研发提供依据。
1 流线型边界方程的理论推导
1.1 流线型边界的提出
缝隙喷口内的流动是三维流动,狭缝出口宽度一般在0.5~5.0 mm左右,喷口长度远远大于宽度,因此,可将这种三维流动状态转化为二维流动进行分析。采用平面势流法,可将流动从求解速度场问题转化为求解势函数和流函数的问题。王英敏等[17]基于东工流线型扩散塔,利用平面势流理论把复杂流动分解成为几种简单流动的叠加,模拟不同结构形式的扩散塔内分流流场和压力场,其模拟结果符合理论分析预期,并在工程实际中验证了平面势流法的可行性。
常规缝隙喷口一般采用锥形收缩的方式,如图1所示[18-19]。其中,W1为缝隙喷口入口宽度,W2为缝隙喷口出口宽度,α是收缩角。水流在进入收缩段和离开收缩段时,易引起边界流动失控而导致阻力损失大和流场失稳,从而进一步影响缝隙喷口形成水幕的稳定性,使缝隙喷口出流不均匀,导致水幕厚度不均匀、成膜后容易扩散、破裂,因此需要对锥形缝隙喷口内部流道边界线进行优化。
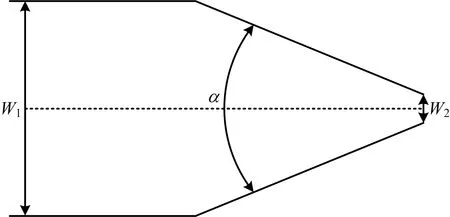
图1 锥形缝隙喷口
1.2 流线型边界方程
将平行段进入收缩段的水流视为平行平面流和点汇的合成流动,建立特定的势函数和流函数。由于喷口关于截面中心线对称,可只研究单侧的边界流线;收缩段的边界流线关于中点M对称,将中点后方的收缩段视作点汇和平行平面流的合成流动,可将整个喷口的边界流线简化为a,b实线所在区域的边界流线,如图2所示。
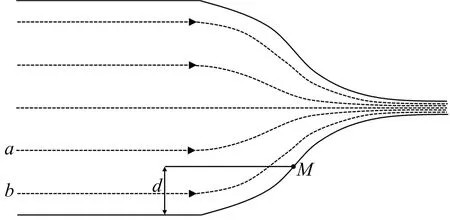
图2 势流叠加示意
平行平面流的复势如式(1)所示:
(1)
式中:Z为复变量;Q为二维平面上的流量,m3/h;d为渐缩段边界中点与平行段的高度差,mm。
考虑喷口较强的对称性,汇流角度取45°,使其收缩角在20°~30°之间,则渐缩管前半段的汇流叠加中的点汇取圆形汇流的1/8,其复势如式(2)所示:
(2)
渐缩管前半段的水流复势为上述平行平面流复势和点汇复势的叠加组成,如式(3)所示:
W(Z)=W1(Z)+W2(Z)
(3)
由此可得出汇流的流函数如式(4)所示:
(4)
式中:θ为角度,以弧度表示;ψ为流函数值。

(5)
当θ取值为π时,y=3d,从工程实际出发,缝隙喷口的边界只需取边界流线的一部分,即θ∈(π/2,28π/36);取修正系数为3,则有式(6):
(6)
2 几何建模
针对边界流线方程取不同θ值得到对应的y值,通过正切函数换算x值,依据得到的x,y值在直角坐标系上进行线性拟合,得到边界流线如图3所示。设定狭缝出口宽度为1 mm,依据所得边界流线,对称绘制形成流线型缝隙喷口的二维边界,如图4所示。
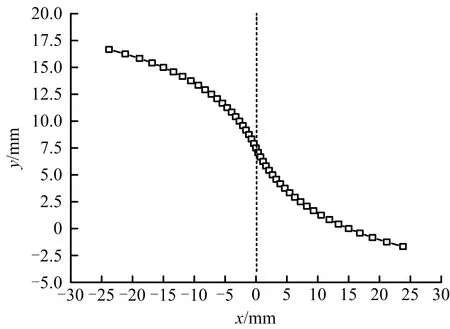
图3 边界流线

图4 流线型缝隙喷口边界
基于图4,在SolidWorks软件中建立流线型缝隙和常规锥形缝隙喷口的三维物理模型,如图5所示。

图5 2种不同结构的缝隙喷口
由图5可知,2种物理模型除边界流线外,其余参数均采取相同设定:进水口直径32 mm,出水口宽度1 mm,出水口长度450 mm,喷口高度71.95 mm,上壁面宽度37.67 mm。
3 控制方程和边界条件
1)控制方程
缝隙喷口内流动介质为液态水,喷口入水口和出口处速度变化大,存在不同程度的湍流,选取能够精确模拟平面和圆形射流的扩散速度,对于有旋流动、流动分离有更好的表现的Realizablek-ε湍流模型进行计算。
2)边界条件
考虑工程用水和隔尘效果的最优化问题,设定模型入口为速度入口,大小为1 m/s,出口设置为压力出口。考虑重力对流场的影响,壁面采用无滑移壁面条件,压力速度耦合方式采用SIMPLE算法,压力离散格式为Second Order,动量、湍动能以及湍流耗散率离散格式均设置为二阶迎风格式,初始化方法选取Hybrid Initialization,计算步长设定为1 000步,收敛判据为进出口流量平衡和残差曲线波动幅度。
4 计算结果与流场分析
对2种缝隙喷口采用抽取线和抽取面的方法,在2个模型上抽取径向截面Ⅰ(x=-0.205 m)、径向截面Ⅱ(x=0 m)、径向截面Ⅲ(x=0.205 m)、轴向截面Ⅳ(z=0 m)4个截面得到相应速度云图、湍动能云图,并在2个模型的缝隙出口抽取中心线得到喷口出口中心线速度分布曲线。分别抽取的Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个截面位置如图6所示。

图6 截面抽取位置
4.1 不同流线结构缝隙喷口内部速度分布
对于锥形缝隙喷口和流线型缝隙喷口而言,2者在不同截面的速度分布云图如图7所示。

图7 2种结构的缝隙喷口速度云图
由图7可知,不同缝隙喷口的流体均在入口段附近受边界结构突扩和壁面黏性力影响,发生流动分离,并且在两侧入水端下侧存在涡旋。其中,流线型喷口在入水端下侧涡旋区域比锥形大。2种结构缝隙喷口中,流体在流动过程中均呈现流速先从两侧入水口逐渐下降,在靠近出口时快速上升的趋势。流线型喷口在出口附近的高流速区相比锥形更宽,这是由于流线型喷口的流道在接近出口时,速度缓慢上升至峰值。
4.2 不同流线结构缝隙喷口内部湍动能分布
对于锥形缝隙喷口和流线型缝隙喷口而言,2者在不同截面的湍动能分布云图,如图8所示。

图8 2种结构的缝隙喷口湍动能云图
湍动能作为湍流强度的度量,可以表征流动中的能量损失。由图8可知,2种结构缝隙喷口均在进水端附近和出口端存在较大的湍动能,这是由于入水端下侧形成的涡旋所致,而出口端则由于过流断面面积收缩明显,流速大幅上升,加剧了流体的湍流脉动;流线型缝隙喷口最大湍动能为0.246 m2/s2,锥型缝隙喷口最大湍动能为0.195 m2/s2,流线型在进水端两侧湍动能强度比锥形更大,这是由于进水端附近渐扩区更大,流体在此减速增压更加明显,旋涡区的增大产生更大的局部阻力损失;在出口端,流线型缝隙喷口湍动能强度大于锥形喷口,这是由于流线型缝隙喷口出口附近具有更宽的高流速区。
4.3 不同流线结构缝隙喷口对出流速度的影响
对于锥形缝隙喷口和流线型缝隙喷口而言,2者出流速度随中心线位置不同的分布曲线,如图9所示。
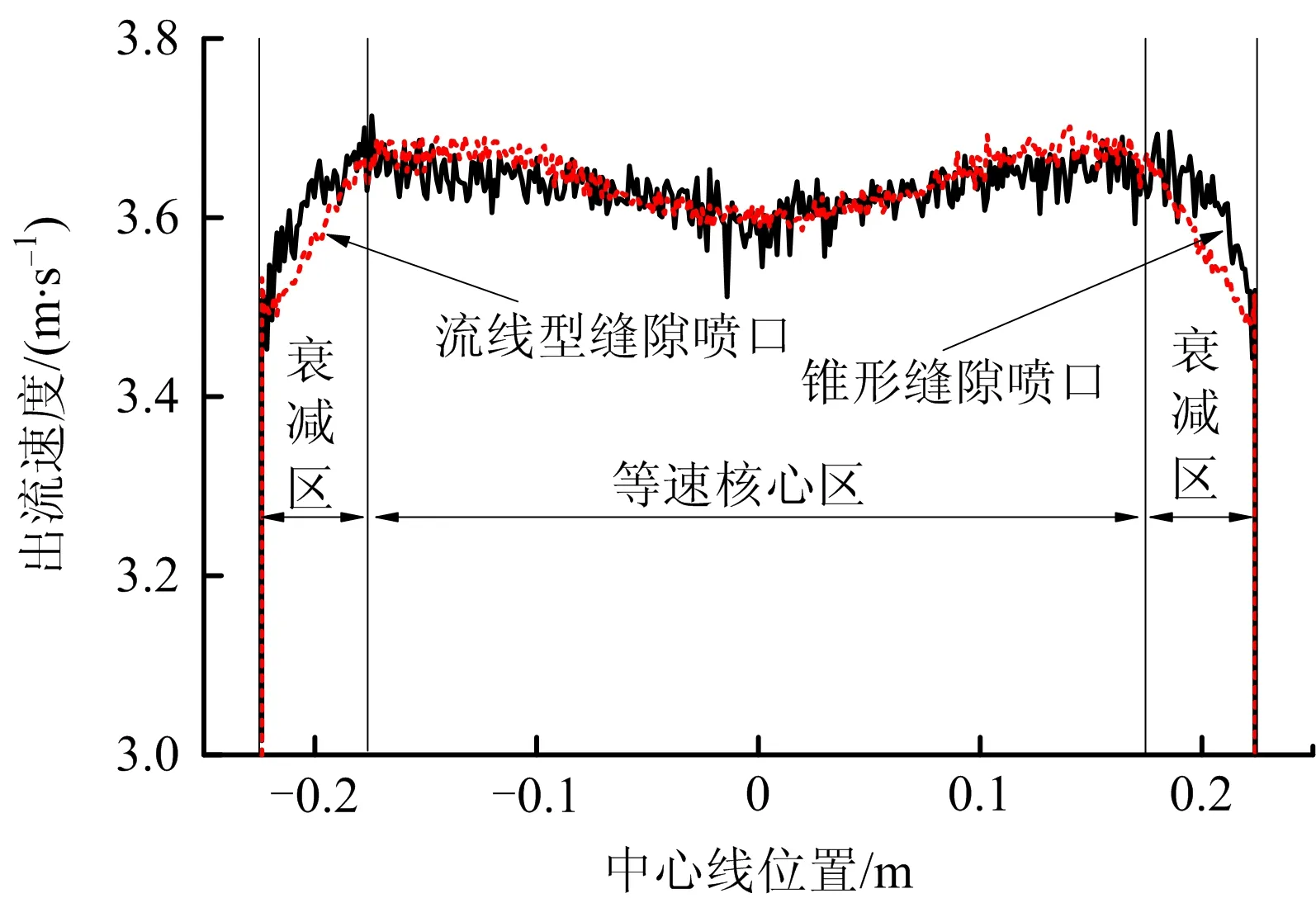
图9 喷口出口中心线速度分布
2种不同结构的缝隙喷口在流速分布均呈现两侧波峰中间波谷式曲线,这是由于缝隙喷口为两端进水结构,两端水流在中心段汇合,轴向速度衰减,因此出流速度曲线中心处出现波谷。锥形缝隙喷口在速度衰减区衰减趋势较流线型平缓,但在等速核心区速度波动幅度大,尤其在曲线中点处出现较大速度波动及下降现象,最小速度为3.51 m/s,而流线型缝隙喷口在等速核心区出流速度曲线波动幅度较小,最小速度为3.58 m/s,这是由于在流线型边界线作用下,喷口内部流动平缓,流场更加稳定。
移动极差MR可以用来描述1组数据的离散程度,如式(7)所示:
MRi=|Xi-Xi+1| (i=1,2,…,k-1)
(7)
式中:Xi,Xi+1分别为第i,i+1个检测值。


图10 不同缝隙喷口的出流速度移动极差
由图10可知,对于完整出流速度曲线,锥形缝隙喷口在中心线位置-0.22 m时出现移动极差最大值0.093 8,移动极差平均数为0.021 5;流线型缝隙喷口在中心线位置0.1 m时出现移动极差最大值为0.049 7,移动极差平均数为0.011 4。采取移动极差平均数作为出流速度离散程度评价指标,对比锥形缝隙喷口,流线型缝隙喷口出流速度离散程度下降46.98%;在等速核心区,锥形缝隙喷口在中心线位置-0.02 m时,出现移动极差最大值0.090 3,移动极差平均数为0.020 5;流线型缝隙喷口在中心线位置0.1 m时,出现移动极差最大值为0.049 7,移动极差平均数为0.011 7。对比锥形缝隙喷口,流线型出流速度离散程度下降42.93%。
5 结论
1)采用平面势流法推导边界流动方程,对流线型缝隙喷口和锥形缝隙喷口进行数值模拟,得到不同喷口出流速度分布,证明流线型边界线用于流道降阻优化的合理性。
2)流线型缝隙喷口相比锥形缝隙喷口而言,在等速核心区出流速度曲线波动幅度较小,并且在全段出流曲线和等速核心区速度离散程度均大幅下降。
3)通过模拟发现,缝隙喷口入水端处存在的流动分离现象,会进一步影响出水端流速衰减快慢。
4)流线型缝隙喷口的内部流场更稳定,出口速度更均匀,可对水幕隔尘用缝隙喷口的研制提供参考依据。
