随机源-荷影响下配电网运行不确定性量化理论方法与应用展望

2022-05-19王晗徐潇源严正惠红勋方晓涛

智能电网 2022年3期

王晗，徐潇源*，严正，惠红勋，方晓涛

（1．电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市闵行区 200240；2．智慧城市物联网国家重点实验室（澳门大学），澳门特别行政区 999078）

0 引言

随着全球气候与环境的日益恶化，大力发展清洁能源，积极推进能源结构低碳化转型已成为全球各国共识[1-3]。以“碳达峰、碳中和”目标为引领，中国提出构建以新能源为主体的新型电力系统，并加速推进用能设施再电气化建设，在此背景下，以分布式风、光发电并网和新型再电气化负荷接入为特征的智能配电网将成为串联能源绿色生产与低碳消费的重要形式[1]。然而，高比例接入的可再生能源发电具有间歇性，大规模异质电力负荷（电动汽车、空调等）具有随机性，均会对配电网运行状态造成显著影响。因此，有必要分析源-荷不确定性的传播过程，研究配电网运行不确定性量化方法，以保障配电网的安全经济运行[3]。

计及随机源-荷的影响，不少学者开展了有关配电网运行不确定性量化方面的研究。考虑可再生能源发电间歇性和负荷波动性，文献[4-9]研究了基于概率潮流计算的配电网潮流不确定性表征问题，所用方法包括模拟法[6]、点估计法[7]、半不变量法[9]等；文献[10-12]研究了考虑源-荷不确定性影响的配电网运行状态感知与估计问题；文献[13-15]引入了基于方差分析的灵敏度分析方法，通过量化指标辨识了显著影响配电网运行状态的关键随机源-荷。上述文献方法均属于配电网运行不确定性量化的研究范畴，但目前并未形成统一的不确定性量化理论研究框架，对随机源-荷影响下量化方法的选择、可适用场景、结果表征形式缺乏系统性论述，影响了不确定性量化理论方法的进一步扩展应用。

针对上述问题，文献[16]从不确定性的定义出发，阐述了不确定性的来源、认知程度分类，以及不确定性分析的典型方法，并给出了建议的综合分析框架；文献[3]从不确定性建模、不确定性因素影响评估、不确定性环境下决策方式，以及不确定性平抑措施四个方面综述了现有研究方法与应对不确定性的手段。上述研究为本文工作的开展奠定了基础，但与上述研究不同，本文侧重不确定性量化理论框架的构建与研究方法的总结，旨在搭建起不确定性认知研究与不确定性应对措施研究之间的桥梁，通过量化表征、科学评估不确定性因素的影响，深化对不确定性因素的本质认识，并为不确定性应对措施的实施提供指导。

本文从配电网源-荷不确定性因素建模出发，针对不确定性量化科学中的前向不确定性传播问题和逆向不确定性评估问题，提出涵盖不确定性表征和灵敏度分析的配电网运行不确定性量化理论框架。在不确定性表征方面，从计算效率和准确性出发，总结现有基于高保真度模型和低保真度模型的不确定性表征方法，并构建兼顾高/低保真度模型特点的多保真度模型；在灵敏度分析方面，引入基于方差、面积和距离的全局灵敏度分析方法，并对比不同灵敏度分析方法的特点与适用场景。最后，展望所提不确定性量化理论方法在耦合系统（如综合能源系统、交通网-配电网耦合系统）中的应用，以期为多时间尺度运行下耦合系统的不确定性分析研究提供方法支撑。

1 不确定性因素建模

1.1 不确定性环境下配电网运行状态的表达

本文以随机源-荷作为输入随机变量，以配电网运行人员所关注的相关指标作为输出变量，构建不确定性环境下反映配电网运行状态的输入-输出响应通用模型：

式中：Y为配电网运行中所关注的指标，即输出变量；ξ为N维输入随机变量。

需要说明的是，针对配电网运行研究中不同的问题，式（1）可扩展为不同的形式，如配电网概率潮流研究中以节点电压、线路功率为输出变量的潮流方程[17]，配电网最大光伏接入能力研究中以光伏最大接纳能力为输出变量的运行风险评估方程[18]等。同时，通用模型的计算过程中也会存在场景生成、模型变换、指标计算等过程。本文利用此通用模型最大化展现所构建的不确定性量化理论框架在配电网运行研究中的适用性与可扩展性。

1.2 不确定性因素的边缘分布

刻画随机源-荷的边缘分布是表征源-荷不确定性的主要手段，常用的方法包括参数模型和非参数模型两种。

1）参数模型：指在历史数据和实际经验的基础上，给定合适的概率分布函数描述输入随机变量的统计特性。参数模型的常用场景包括利用正态分布刻画负荷预测误差概率分布、利用威布尔分布刻画风速概率分布、利用Beta分布刻画光照强度概率分布等。在实际应用中，需要根据配电网所处区域随机源-荷的类型和特点选取概率分布函数。

2）非参数模型：指利用源-荷的历史数据，研究其分布特征并给出概率分布函数。核密度估计是一种常用的非参数模型构建方法[19]，其利用多个平滑的核函数来刻画样本点附近的分布特征，并采用线性叠加的方式给出概率分布函数。在实际应用中，非参数模型需要大量的数据作为支撑。

基于配电网源-荷历史数据，参数模型构建过程中，运行人员会根据先验知识，指定特定的概率分布函数（如正态分布、威布尔分布和Beta分布）刻画输入随机变量的边缘分布，而由于主观认知不确定性的影响，所指定的分布函数可能会与实际概率分布函数之间存在较大误差，从而导致参数模型拟合精度较低。非参数模型不依赖于事先假定的边缘分布函数，能够最大化利用数据本身的分布特征获取输入随机变量的概率分布函数，但其计算过程中存在边界效应，且最优宽度的选取也会影响非参数模型的拟合精度。因此，实际计算中需要兼顾人为经验和数据分布特征，适时选择不确定性因素的边缘分布刻画方法，尽可能提高计算精度。

1.3 不确定性因素的相关性

由于区域内气象环境、负荷特征的相似性，配电网内随机源-荷之间存在着不同程度的相关性，在利用边缘分布函数表示单个输入随机变量的统计特征后，还需要进一步刻画多维输入随机变量之间的相关性。目前，常用的相关性刻画方法包括线性相关系数和Copula函数。

1）线性相关系数。

线性相关系数也被称为Pearson相关系数，在现有研究中是最为常用的相关性度量指标[20]。线性相关系数的取值区间为[-1,1]，正、负值分别表示随机变量间正、负相关性，其绝对值越大表示随机变量间的相关程度越高。在配电网不确定性因素建模过程中，线性相关系数获取方便且易于计算，但线性相关系数不能用于表征随机变量间非线性的相依关系，具有一定的局限性[21]。

2）Copula函数。

Copula函数是刻画多维随机变量相关性的重要手段，通过连接多个随机变量的边缘分布，从而实现多维随机变量联合概率分布函数的构建。常用的刻画多维（三维及以上）随机变量间相关性的方式包括椭圆Copula函数族和Vine Copula方法。

椭圆Copula函数族包括Gaussian-Copula和T-Copula，其能够直接应用于三维及以上随机变量间相关性的刻画，但所得相依结构始终是对称的，难以捕捉随机变量间相依结构的非对称特性。

Vine Copula方法通过引入藤结构将不同类型的Copula函数组合起来，并采用逐层依次合并的方式建立随机变量的联合分布函数，主要包括D-Vine和C-Vine两种结构类型[22]。Vine Copula方法所构建的相依结构，能够刻画多维随机变量间非线性的相依关系，有效弥补线性相关系数方法的不足，但Vine Copula方法增加了计算的复杂性，且随机变量维数越高，计算复杂性增加越明显。

值得说明的是，不确定性因素建模完成后需要通过采样的方式获得随机源-荷样本，对于采用线性相关系数刻画随机变量之间相关性的场景，需要引入Nataf变换[23]实现样本生成；对于采用Vine Copula方法刻画随机变量之间相关性的场景，需要引入Rosenblatt变换[24]实现样本生成。

2 不确定性量化理论方法

基于不确定性因素模型和系统输入-输出关系，从不确定性量化理论需要解决的问题入手，本章构建配电网运行不确定性量化理论框架，提出不确定性表征和灵敏度分析两个不确定性因素影响量化环节，并分别总结现有可行方法，为不确定性量化理论的应用与拓展研究奠定基础。

2.1 配电网运行不确定性量化理论框架

不确定性量化（uncertainty quantification，UQ）是实现不确定性环境下系统输出特征表征和输入因素影响评估的科学，主要包括两类研究问题[25]：①前向不确定性传播问题，指输入不确定性因素在系统内传播后，系统输出响应特征的量化表征问题；②逆向不确定性评估问题，指获得系统输出响应特征量后，对输入不确定性因素的影响评估与参数校正问题。从上述两类研究问题出发，针对随机源-荷影响下的配电网运行不确定性量化研究，本文提出了如图1所示的不确定性量化理论框架，包括不确定性表征和灵敏度分析两个环节。其中，不确定性表征环节用于解决随机源-荷影响下配电网内前向不确定性传播问题（对应图1中过程①、②、③），灵敏度分析环节用于实现随机源-荷对配电网运行状态影响程度的逆向量化评估（对应图1中过程④、⑤）。利用所提出的不确定性量化理论，能够准确量化随机源-荷对配电网运行状态变量的影响，辨识具有显著影响的关键随机源-荷，为储能装置的优化运行策略、量测装置的配置点选择提供指导。同时，仅保留关键源-荷降低了复杂随机问题的处理维度，有利于提升配电网运行分析的效率。基于所提不确定性量化理论框架，本文后续将着重介绍不确定性表征和灵敏度分析环节中所涉及的具体方法，为不确定性量化理论的应用提供支撑。

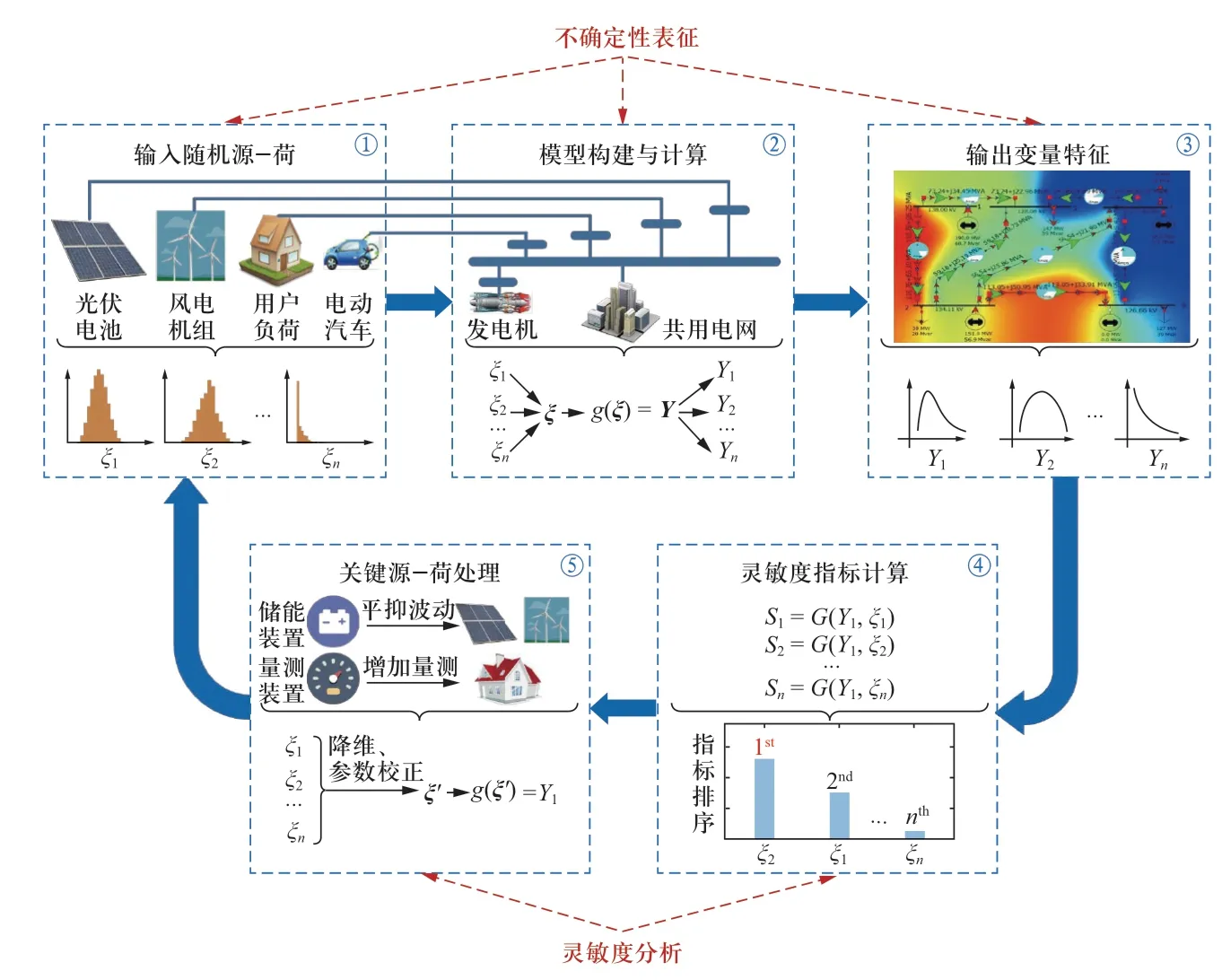
图1 配电网运行不确定性量化理论框架Fig.1 Framework of uncertainty quantification theory for distribution network operation

2.2 不确定性表征方法

不确定性表征以系统输出响应的统计特征为量化指标表征输入随机变量（如配电网随机源-荷）的影响，常用的量化指标包括输出响应的均值、方差、概率密度函数（probability density function，PDF）和累积分布函数（cumulative distribution function，CDF）。在不确定性表征的过程中，如何快速、准确地实现上述量化指标的计算一直是研究人员重点关注的问题。针对该问题，本文从计算效率和准确性两方面出发，总结现有基于高保真度模型和低保真度模型的不确定性表征方法，并提出基于多保真度模型的不确定性表征方法。

2.2.1 基于高/低保真度模型的不确定性表征方法

在配电网运行分析中，给定输入随机变量数据，通常有两种方式获得输出响应的结果：①建立复杂、精细化的高保真度模型，在给定输入下获得高精度的输出结果，但需要付出极高的计算成本；②通过线性化、逼近等手段建立低保真度模型，在给定输入下获得近似的输出结果，但所付出的计算成本较低。如图2所示，对比高/低保真度模型的计算成本和计算误差可知，低保真度模型以牺牲计算精度为代价换取了计算效率的提升。

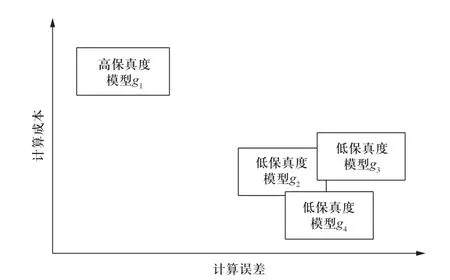
图2 高保真度模型与低保真度模型对比Fig.2 Comparison of high-fidelity and low-fidelity models

现有配电网运行状态不确定性表征方法同样可以划分为不同保真度模型计算的范畴。其中，以基于原始物理模型的蒙特卡洛模拟（Monte Carlo simulation，MCS）为基础的方法均属于高保真度模型计算的范畴，包括基于简单随机采样的MCS方法[26]、基于拉丁超立方采样的MCS方法[27]、基于Sobol序列的MCS方法[28]等；以点估计法为代表的近似法[29]、以半不变量法为代表的解析法[30]和基于代理模型的MCS方法[31]均属于低保真度模型计算的范畴。为提升不确定性表征过程的计算效率，低保真度模型构建方法一直是不确定性表征方法研究的重点。其中，通过代理模型替换原始物理模型的MCS方法是近几年研究中的热点话题，常用的代理模型构建方法包括多项式混沌展开法〔如随机响应面法（stochastic response surface method，SRSM）[32]、广义多项式混沌法（generalized polynomial chaos method，gPCM）[33]、稀疏多项式混沌展开（sparse polynomial chaos expansion，SPCE）[34]〕，低秩逼近（low-rank approximation，LRA）[35]，高斯过程回归（Gaussian process regression，GPR）[36]，人工神经网络（artificial neural networks，ANN）[37]，支持向量回归（support vector regression，SVR）[38]。值得说明的是，近年来不少代理模型辅助构建平台迅猛发展，包括UQLab[39]、Libsvm[40]、UQ-PyL[41]等，上述平台工具的运用为基于低保真度模型的不确定性表征方法扩展应用提供了有力支撑，多种代理模型详细构建过程与对应平台工具的功能介绍可参见文献[42]。

2.2.2 基于多保真度模型的不确定性表征方法

考虑高保真度模型与低保真度模型在计算准确性和计算效率方面的互补性，近年来不少学者研究了高/低保真度模型相结合的多保真度模型构建方法。文献[43]描述了多保真度问题的一般形式，并指出利用多保真度模型能够降低输出响应结果的计算成本且保证计算精度；文献[44]提出了基于多保真度建模的层次回归模型；文献[45-47]研究了多保真度的Monte Carlo估计方法，以提升传统MCS方法的计算效率。上述工作为不确定性表征方法中多保真度模型的应用奠定了基础。

考虑配电网输出状态变量的均值和方差指标，本文引入一种多保真度Monte Carlo估计模型[48]，以实现系统输出响应均值、方差的高效计算。假定M=[M(1),M(2),…,M(k)]为k维样本规模向量，M(1)＞0且k≥l＞g≥1时M(l)＞M(g)，给定M(k)组输入随机变量样本[ξM(1),ξM(2),…,ξM(k)]，输出响应Y的多保真度均值与方差估计结果可表示为

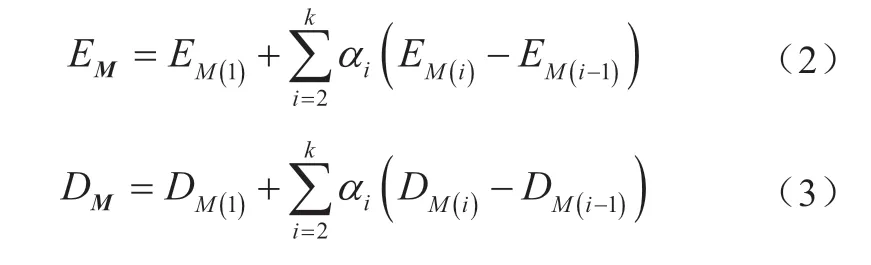
式中：α2,α3,…,αk为多保真度均值、方差估计模型的控制系数；EM(1)、DM(1)分别为1个高保真度模型在给定M(1)个输入随机变量样本ξM(1)下输出响应Y均值和方差的计算结果；EM(i)、DM(i)（i= 2,3,…,k）为第i-1个低保真度模型在给定M(i)个输入随机变量样本下输出响应Y均值和方差的计算结果。

文献[48]和[49]证明式（2）和（3）所得结果是高保真度模型所得均值和方差的无偏估计（unbiased estimator）。进一步，根据给定可接受的计算负担（即计算时间）、不同低保真度模型的单次计算负担（即计算时间）、低保真度模型输出响应结果与高保真度模型输出响应结果间的相关性，可通过优化问题求解确定多保真度均值、方差无偏估计模型中的控制系数α2,α3,…,αk，从而实现不确定性表征中均值和方差的高效计算，具体流程可参见文献[49]。值得说明的是，多保真度模型可基于所选择的低保真度模型构造不同的形式，典型的多保真度模型还包括co-Kriging模型[50]、多保真度径向基函数（radial basis function，RBF）模型[51]等，其在不确定性表征中的应用具有很大的探索空间。

2.3 灵敏度分析方法

灵敏度分析以输出变量相对于输入随机变量的灵敏度为量化指标，用于反映各个输入不确定性因素对系统输出的影响程度，常用的灵敏度分析方法包括局部灵敏度分析（local sensitivity analysis，LAS）和全局灵敏度分析（global sensitivity analysis，GSA）。LSA用于评估参考运行点附近单个输入变量波动（幅度在±10%以内）对系统输出的影响。然而，当输入变量的随机波动范围较大时，系统参考运行点会发生偏移，此时LSA便不再适用。为弥补LSA的不足，近年来GSA被应用于量化电力系统内随机源-荷的影响[52]。GSA能够考虑输入随机变量的整个分布范围及分布特性，从而实现多种不同特征的输入随机变量影响量化。本文总结了几种常用的GSA方法，并对比了不同GSA方法的特点及其在配电网运行不确定性量化研究场景中的可用性。

2.3.1 基于方差的GSA方法

文献[53]中，数学家I.M.Sobol基于方差分析（analysis of variance，ANOVA）理论提出了基于方差分解的GSA方法，并定义了全局灵敏度指标。给定N维独立输入随机变量ξ=(ξ1,ξ2,…,ξN)，对于定义在ΩN={ξ|0≤ξi≤1,i=1,2,…,N}空间的输出响应Y=G(ξ)，可得方差分析的高维模型表示：

式中：D为输出响应Y的总方差；Dm…n（1≤m≤n≤N）为输出响应Y的偏方差。

进一步，定义输入随机变量ξi的一阶灵敏度指标Si和总灵敏度指标ST,i如下[53]：

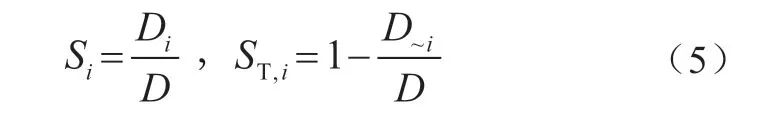
式中：D～i为所有Dm…n（i∉[m,n]，1≤m≤n≤N）之和。

上述一阶灵敏度指标（first-order sensitivity index，FSI）反映了输入随机变量ξi对输出响应Y的影响程度，FSI值越大，ξi的不确定性对输出响应Y的影响越大；全局灵敏度指标（total sensitivity index，TSI）反映了输入随机变量ξi本身以及ξi与其他输入随机变量的交互作用对输出响应Y的共同影响，TSI值越大，共同影响程度越大。需要注意的是，若输入随机变量间相互独立，则ξi的TSI始终大于其FSI[53]。利用FSI和TSI，基于方差分解的GSA方法已应用于配电网的概率潮流分析[54]、配电网分布式光伏的关键参数辨识[55]、配电网负荷参数建模[56]、配电网状态估计[14]等研究。

2.3.2 基于面积的GSA方法

基于面积的GSA方法通过量化PDF（或CDF）与相应的条件PDF（或条件CDF）之间的差异面积作为全局灵敏度指标，以评估输入随机变量的影响。文献[57]中所提出的Borgonovoδ方法就是一种典型的基于PDF间差异面积计算的GSA方法，对于输出响应Y，Borgonovoδ方法定义全局灵敏度指标：

式中：fY(Y)为考虑所有输入随机变量影响时输出响应Y

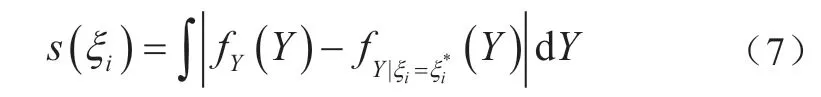
如图3所示，阴影部分面积即为差异面积s(ξi)，利用式（6）中的积分计算获得差异面积的期望，从而实现输入随机变量ξi对输出变量Y的影响评估。对于独立的输入随机变量，文献[57]证明的取值范围为[0,1]，值越大，输入随机变量ξi对输出响应Y的影响程度越大。

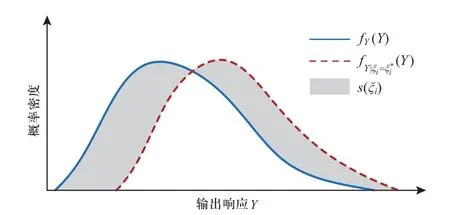
图3 基于PDF的差异面积示意图Fig.3 Diagram of area difference based on PDF

由于PDF的估计问题是不适定的[58]，准确估计PDF比较困难且存在计算过程收敛慢、带宽计算复杂等缺点[59]，针对此问题，文献[60]提出利用CDF与条件CDF之间的差异面积定义全局灵敏度指标：

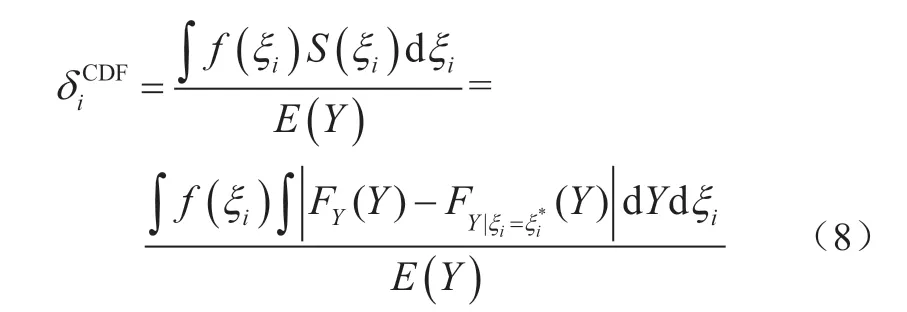
式中：FY(Y)为考虑所有输入随机变量影响时输出响应Y的CDF；为第i个输入随机变量ξi为固定值其他输入变量随机变化时输出响应Y的条件CDF；E(Y)为输出响应Y的均值；S(ξi)为Y的CDF与其条件CDF之间的差异面积，表示为

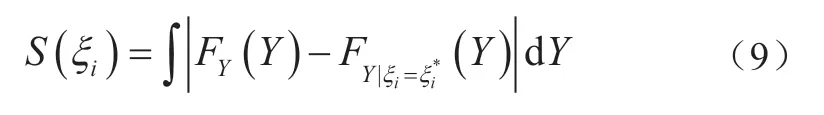
如图4所示，阴影部分面积即为差异面积S(ξi)，利用式（8）中的积分计算差异面积的期望占比，从而实现输入随机变量ξi对输出变量Y的影响评估。需要注意的是，当输出响应的均值为0时，规定式（8）中的分子项即为相应的全局灵敏度指标。目前，基于面积的GSA方法已应用于电力系统概率小干扰稳定分析[61]、孤岛微电网概率潮流计算[4]等研究。

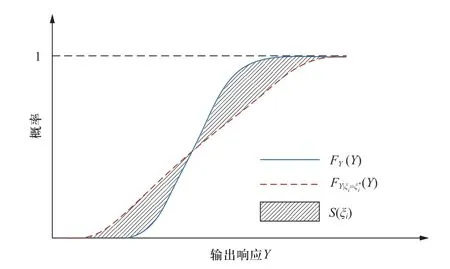
图4 基于CDF的差异面积示意图Fig.4 Diagram of area difference based on CDF

2.3.3 基于距离的GSA方法

基于距离的GSA方法通过量化CDF与相应的条件CDF之间的距离作为全局灵敏度指标，以评估输入随机变量的影响。文献[62]提出利用Kolmogorov-Smirnov（K-S）距离定义全局灵敏度指标：

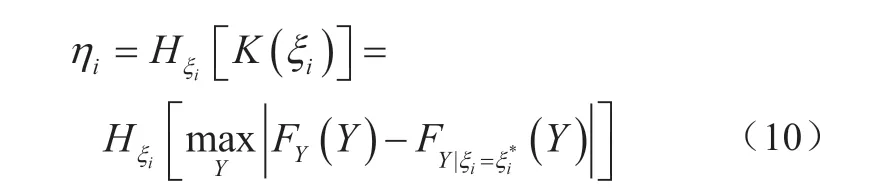
式中：Hξi[·]为输入随机变量ξi取不同固定值时输出响应Y的CDF与其条件CDF间K-S距离的最大值（或中位数）；K(ξi)为Y的CDF与其条件CDF之间的K-S距离，如图5所示。

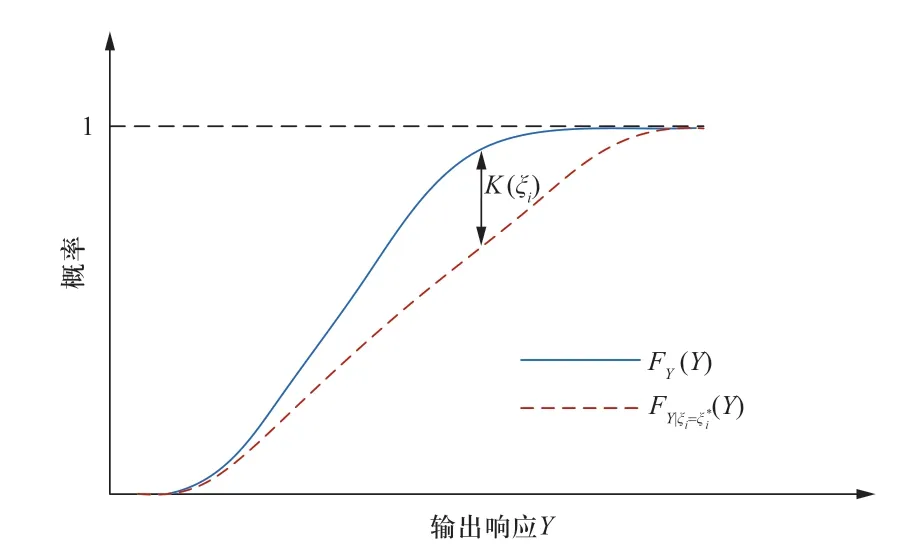
图5 基于CDF的K-S距离示意图Fig.5 Diagram of K-S distance based on CDF

文献[62]指出通过式（10）计算所得全局灵敏度指标ηi取值范围为[0,1]，ηi值越大，表明输入随机变量ξi对输出响应Y的影响程度越大。

表1对比了基于方差、面积和距离的三种GSA方法的特点与配电网运行中的适用场景。相比而言，基于方差分析的GSA方法计算效率高，但仅利用方差反映输出随机特征具有一定的片面性；基于距离的GSA方法尽管也利用了输出响应的分布函数计算全局灵敏度指标，但其计算过程不需要积分计算，相比基于面积的GSA方法具有更高的计算效率；但由于距离计算结果的差异性较小，所得重要性排序结果具有一定的局限性。

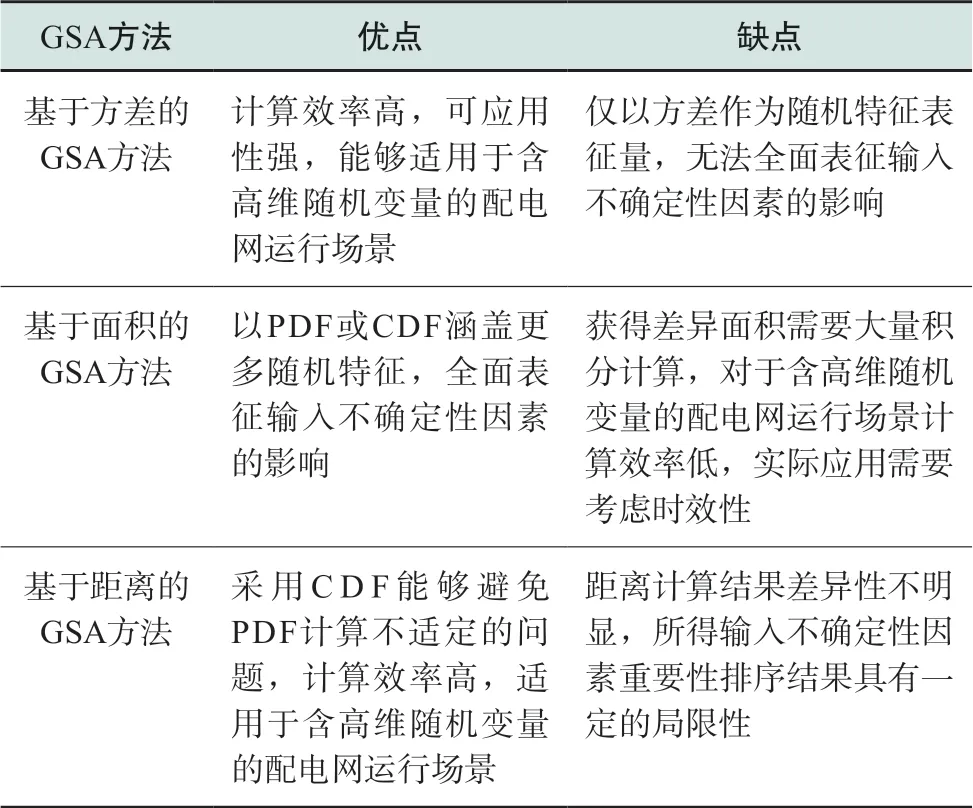
表1 不同GSA方法对比Table 1 Comparison of various GSA methods

3 耦合系统中不确定性量化理论应用展望

随着能源转型战略的实施，以电力为主要媒介的耦合系统不断发展，并逐渐成为消纳绿色能源的关键范式。目前研究中，典型的耦合系统包括综合能源系统和交通-电力耦合系统。耦合系统各主体内含有特性各异的多重不确定性因素，伴随多时间尺度下耦合系统间的不断运行交互，多重不确定性因素的传播将直接影响耦合系统的安全运行。因此，有必要进一步展望所提配电网运行不确定性量化方法在耦合系统中的应用，主要包括以下三个方面。

3.1 耦合系统内多重不确定性因素交互影响量化

考虑多时间尺度运行，建立计及不确定性因素影响的耦合系统运行特征表征模型，研究不确定性环境下各子系统间的耦合交互运行机理，量化不确定性因素通过耦合环节对各子系统运行状态的影响。具体而言，对于综合能源系统，利用不确定性表征方法，研究不确定性因素影响下系统概率多能流计算过程与表征方式；利用全局灵敏度分析方法，研究电、热、气子系统内不确定性因素经能量集线器后对异质能流波动的影响。对于交通-电力耦合系统，研究基于不确定性表征的交通流-电力流概率特征量化方法，构建适用于交通流、电力流均衡特征刻画的高/低保真度模型，分析道路容量波动性、出行需求随机性、可再生能源出力间歇性对交通-电力概率联合流的影响，辨识影响耦合系统运行状态波动的关键不确定性因素，从而为复杂不确定性环境下耦合系统的优化运行提供指导。

值得说明的是，不确定性因素在耦合系统内的传播具有时滞性，如电力网络注入功率的瞬时波动并不能导致热力系统温度的瞬时变化；交通流量的实时变化并不会瞬时影响路段充电站负荷的波动。因此，耦合系统的运行分析需要采用多时间尺度下的模型，这使得不同时间尺度下随机输入变量的影响难以利用局部灵敏度分析方法量化，而本文所提全局灵敏度分析方法考虑的是不确定性因素长时间尺度下的概率分布特性，从而将不确定性因素的影响表征与量化过程置于同一时间尺度下，在不确定性环境下耦合系统的运行分析中具有优势。

3.2 耦合系统内不确定性因素间相关性的影响评估

耦合系统内不确定性因素间相关性复杂，尽管本文1.3节已给出常用的不确定性因素相关性刻画方法，且现有不确定性量化分析的研究也常以独立和相关两种不同场景为研究对象，给出考虑不确定性因素间相关性的分析结果，但实际上目前大多数研究均仅停留在不确定性表征阶段，以获得考虑相关性场景下输出变量的均值、方差、概率分布为目标，较少涉及不同程度相关性、不同相依结构对输出变量影响程度的量化研究。目前，不确定性因素间相关性的影响量化问题仍处于基础理论探索阶段，且耦合系统内多维、异质的不确定性因素间相关性复杂，需要进一步开展理论方法与应用验证，实现从理论研究到应用实践的突破。近年来，文献[63]研究了源-荷不确定性及相关性对区域电-气联合系统运行的影响，文献[64]定义了量化随机变量间相关性影响的全局灵敏度指标，均是对不确定性因素间相关性影响量化问题的有益探索。

3.3 考虑认知不确定性的不确定性量化理论研究

根据文献[65]和[66]可知，不确定性分为随机不确定性和认知不确定性。随机不确定性指规律演化中物理事物本身存在的固有特性，其不随样本数量的增加而发生改变；认知不确定性指由于知识或数据缺失、人类主观认识不足而导致的模型构建或参数刻画不准确[67]。一般情况下，随机不确定性能够用概率分布函数刻画，而认知不确定性可通过非概率方法（如模糊集理论）表征。本文所提出的不确定性量化方法主要针对随机不确定性而言，暂未考虑认知不确定性的影响，但实际耦合系统运行中存在大量的认知不确定性。具体而言，多时间尺度下综合能源系统的多能流模型存在多处简化处理；可再生能源发电数据按时间周期聚类存在主观性，导致随机模型参数具有模糊性；交通网-配电网耦合系统内用户出行路线的选择具有偏好性，导致均衡模型中出行需求的刻画具有认知不确定性。因此，在现有随机不确定性量化方法的基础上，如何考虑认知不确定性因素的影响，进一步扩展不确定性量化理论在耦合系统内的应用范围需要进一步研究。文献[68]提出了一种基于模糊分布参数的全局灵敏度分析方法，文献[69]提出了考虑源-荷随机-模糊特征的配电网潮流不确定性量化方法，为考虑认知不确定性的不确定性量化理论研究提供了新思路。