数据驱动的高比例新能源发电集群分布式电压控制

钟成元，桂前进*，江千军，徐文法，黄昊，郭力，王中冠

（1.国网安徽省电力有限公司安庆供电公司，安徽省 安庆市 246003；2.天津大学电气自动化与信息工程学院，天津市 南开区 300172）

0 引言

国家“双碳”战略的制定明确了建设新型电力系统目标，电力系统的创新和转型升级已成为必然[1-2]。近年来，分布式发电快速增长，呈现出集群化发展趋势，多地提出建设整县分布式光伏发电，使得越来越多的区域配电网电源渗透率不断提升，形成高比例新能源发电集群[3-4]。

然而，由于新能源发电天然具有的不确定性，接入配电网的发电集群出力常常呈现明显的波动。随着新能源装机容量的持续增长，配电网及新能源发电集群的运行控制正受到严峻的挑战[5-7]。由于新能源接入电网末端改变了单一的潮流流向，造成局部消纳困难问题的同时，可能导致末端电压抬升和网损增加问题，不仅影响用电器寿命，更可能造成由电压越限导致的电源脱网和供电中断事故[8]。

与此同时，现有的配电网电压运行控制方法主要依赖于传统的控制设备，例如有载调压变压器和电容器档位的调节，由于设备特性限制，其控制时间尺度远大于新能源发电出力变化尺度，导致传统方法无法有效应对随机波动[9]。相比传统无功控制设备，新能源发电并网变换器自身的无功调节能力能够对电压控制起到关键作用，保障系统的安全高效运行。因此，成本更低、响应更快的通过调节变换器无功输出而改善电压分布的方式受到了广泛的关注[10-12]。

事实上，若集群调控系统可快速完整获取全局模型与运行状态信息，电压优化控制的本质即是最优潮流问题的求解。在集中式策略下，集中控制器与所有新能源发电变换器通信并下发控制指令。然而，集中式控制需要复杂的通信以采集并处理大量数据，因此控制时延较长，且可能遭遇单点故障问题[13-14]。考虑到集群状态的快速变化，通信时延将影响系统稳定性，网络结构的变化也需要对控制模型进行重新维护，影响了供电可靠性。

与之相比，分布式控制模式由于降低了集中计算负担，能够显著提升电压控制的响应速度[15-16]。在此概念基础上，一些分布式控制方法采用多代理系统，在相邻节点之间实现信息交互[17-18]。例如，文献[19-21]采用交替方向乘子法，而文献[22]则开发了基于次梯度迭代的求解器以实现配电网最优无功调度。由此可见，在具有完整模型的高比例新能源发电集群中，采用基于次梯度算法的分布式电压控制策略能够实现大规模可控对象的高效协调，改善集群电压分布。

电压控制问题与潮流分布密切相关，分布式迭代控制虽然无需集中模型维护和求解，但仍需各可控对象获取相邻支路的阻抗参数，以此计算每步迭代中的功率调整方向。因此，一旦集群支路模型不完备，或阻抗参数存在较大误差，势必将对分布式电压控制迭代产生不良影响[23]。现行电网运行调度体系中，调度中心不掌握大多数中低压配电网完整的阻抗参数信息，将导致分布式电压控制效果与速度受限。

在模型不完备的中低压新能源发电集群中，利用节点量测数据样本，通过数据驱动方式建立等效潮流模型，实现精确潮流计算是一种可行的替代思路[24-25]。节点电压与电源无功之间的潮流约束为非线性方程，根据空间变换理论，低维空间下的非线性模型，在高维空间中可通过升维变换表示为线性方程而不影响模型精度[26]。因此，以历史运行数据作为训练样本，通过数据驱动方式，能够得到节点电压与电源无功间的高维线性化方程，从而计算分布式电源控制过程中的精确迭代方向。

本文提出一种基于数据驱动的迭代方向修正方法，利用各节点海量运行量测数据样本，基于Koopman升维线性化得到高精度全局潮流模型，并以此离线校正分布式次梯度电压控制的迭代方向，避免模型不精确对迭代收敛性与控制效果的影响。

本文内容主要安排如下：第1章基于线性潮流推导给出在假设具备完整模型参数的前提下，基于次梯度法的分布式电压控制迭代策略，第2章构建数据驱动的分布式电压控制架构，并介绍基于Koopman数据驱动方法训练高精度潮流模型及计算分布式迭代方向的方法，从而实现不依赖于精确模型参数的电压控制，其控制方法算例效果分析在第3章给出，第4章总结全文。

1 集群电压控制模型与迭代策略

1.1 基于线性潮流的集群电压模型

本文讨论的新能源发电以分散形式接入配电网，新能源发电装机容量占负荷需求比例较高，形成高比例发电集群。由于有功功率在线路末端的注入，集群中各节点出现电压越限风险。通过对大量新能源发电单元的协调控制，调整新能源输出的无功功率，能够显著改善集群中的电压分布。

本章首先在假设存在精确模型参数的前提下构建集群电压优化控制模型。需要强调的是，本文提出的电压控制方法并不需要获取精确模型参数，但本文控制方法的理论依据建立在对基于模型的电压控制方法的改进之上，因此本章需首先对无功-电压控制模型进行介绍。

中低压配电网拓扑主要为辐射状，因此本章模型针对辐射状网络进行分析，但本文方法并不局限于辐射状网络，对存在环网的情况同样适用。为方便表达，定义N ={0,1,…,N} 表示集群各节点所构成的集合，表示节点对(i,j)间的支路所构成的集合。定义节点0代表集群参考节点，一般情况下代表所接入变电站的低压母线，即辐射状网络的根节点。其余变量定义如图1所示。

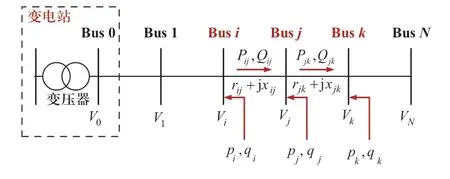
图1 集群电压控制模型中的变量定义Fig.1 Notation of voltage control model of cluster

如图1所示，定义Vi代表节点i的电压幅值，pi和qi分别代表节点i的有功功率和无功功率注入值，rij和xij分别代表支路(i,j)的支路电阻与电抗值，Pij和Qij分别代表由节点i首端流向节点j的有功功率和无功功率。此外，为方便表示，定义节点i的下游相邻节点，即相较节点i更加远离参考节点，并与节点i之间具有支路直接相连的节点所构成的集合为。例如图1中，节点j就为集合Ni中的全部元素。

根据上述定义，基于支路潮流约束，可得到如下的支路形式线性化潮流方程：

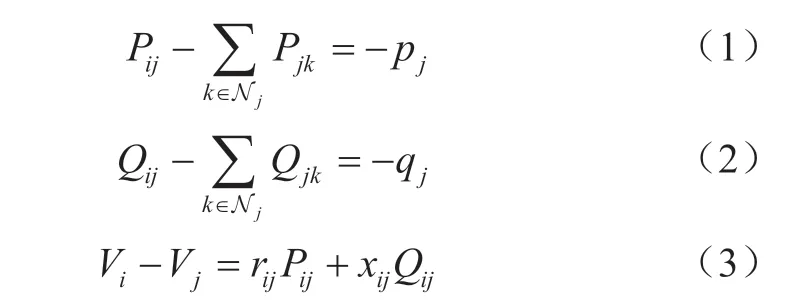
该线性化模型忽略了网损所对应的非线性项，并假设电压标幺值接近1，因此其精度有限。但该模型仅用于后续分布式电压控制的推导分析，并非用于电压控制结果的精确推导计算，因此不影响电压控制的精度。

定义M0代表新能源集群网络的完整节点-支路关联矩阵，由于假设分析对象为辐射状网络，易知其矩阵维数为N×N(－1)。根据定义，若节点j∈Ni，则矩阵M0中的元素且，其中l为支路(i,j)的编号。易知，完整节点-支路关联矩阵M0的行与列之和均为0，在矩阵M0的基础上，删去参考节点0所对应的第1行，用矩阵符号M代表剩余部分的(N-1)×(N-1)维节点-支路关联矩阵。由于删去首行，矩阵M为满秩方阵，可以进行求逆运算。基于节点-支路关联矩阵M，式（1）与式（2）的支路有功、无功方程可改写为矩阵形式：

式中：向量P和Q分别代表由支路有功功率Pij和无功功率Qij所构成的列向量，而向量p和q则分别代表由节点注入有功功率Pij和无功功率Qij所构成的列向量。在集群电压控制问题中，通常假设参考节点电压为固定值，此处不妨假设变电站低压侧母线电压满足V0=1，则支路电压方程（3）可采用矩阵形式表达如下：

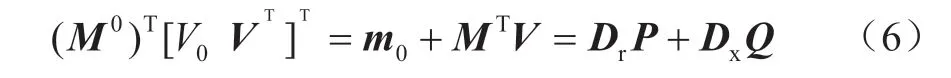
式中：向量V代表由节点电压幅值构成的列向量；代表矩阵M0中的第一行，也即对于参考节点的一行；矩阵Dr和Dx则分别代表对角元素为rij和xij，而其他元素均为0的N×N阶对角矩阵。将支路有功、无功方程（4）和（5）代入支路电压方程（6），可得到电压向量V与节点注入功率间的线性关系如下：

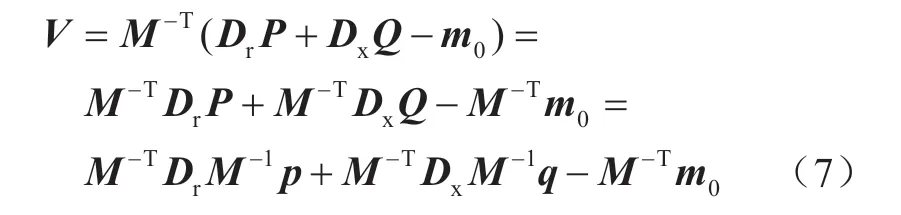
其中，为简化表达，M-T代表MT的逆矩阵。

进一步定义矩阵R和X分别为

则电压方程（7）可简化为

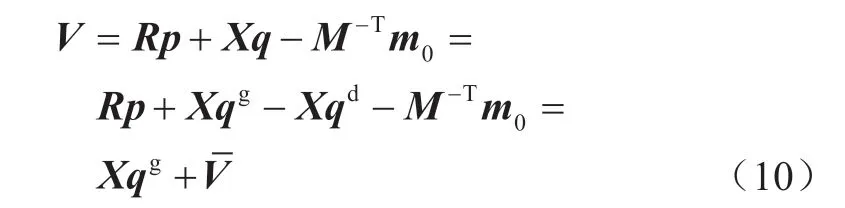
式中：向量qg代表由节点i电源无功注入构成的向量；向量qd代表由节点i负荷无功需求构成的向量；向量代表新能源发电集群的天然电压分布，即电源无功注入不进行优化控制下的电压分布：

线性模型（10）即参数完备下的集群潮流电压约束方程，可作为分布式电压控制的依据。

1.2 基于次梯度法的分布式电压控制策略

1.2.1 电压优化控制模型

本文电压优化控制主要在给定的电源有功发电功率（一般为最大功率跟踪模式）及负荷有功、无功值的前提下，通过调节新能源发电无功功率qg实现改善集群电压分布的目标，即优化变量为qg。

1）目标函数。

电压优化目标为各节点电压幅值与额定电压偏差的平方和最小，即

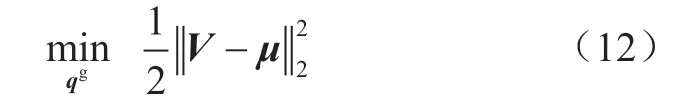
由于优化问题应满足潮流电压方程（10）的约束，为清晰表述节点电压与电源无功注入的关系，将式（10）代入式（12），得到目标函数的新形式：

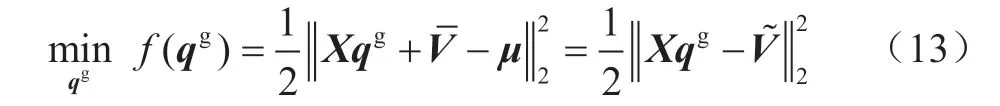
2）约束条件。

电压控制中，需要满足的约束条件包括潮流平衡约束、电源无功调节能力约束、节点电压上下限约束、线路载流量约束等。其中潮流平衡约束在1.1节中线性化的支路潮流方程中已考虑，并通过代入目标函数体现了电压与无功之间的潮流约束。而受限于分布式次梯度法仅能求解盒约束（即各变量约束彼此独立）凸优化问题的限制，本文暂不考虑节点电压上下限约束和线路载流量约束。事实上，由于目标函数的设置，集群各节点电压将尽可能接近额定值，而在实际工程中，配网线路容量的冗余性亦不会明显制约无功流动。

针对各电源无功调节能力受逆变器容量的限制，本文将其表示为优化变量的有界约束，即

因此，式（13）及式（14）构成了完整的有界约束二次规划电压优化控制模型。在参数完备的条件下，采用集中式方法可以非常方便地进行求解。然而，由于前述原因，本文需采用分布式方法进行求解，模型参数不完备的处理方法在第2章中给出。

1.2.2 基于次梯度法的分布式电压控制

为解决集中式电压控制存在的通信时间长、模型维护困难、可靠性低的问题，本文采用分布式反馈电压控制的模式，通过新能源发电控制器的协调自治，实现对电压优化控制模型的分散求解，同样能够得到最优无功策略。方法的主要步骤为：

1）各新能源发电单元采集本地节点电压、无功注入等信息；

2）通过支路直接相连的新能源发电单元间交互各自节点电压信息；

3）各分布式发电单元根据本地信息及相邻新能源发电单元信息，调整无功功率；

4）重复上述步骤，直至迭代达到收敛。

分布式反馈控制的优势在于，无需集中模型求解，对模型维护及参数精度要求较低；无需待求解完毕后再发布控制指令，响应速度更快，适合波动性较强的新能源发电集群；对通信可靠性要求更低，仅需点对点通信构成连通拓扑，即可保证控制收敛。分布式反馈控制的架构如图2所示。

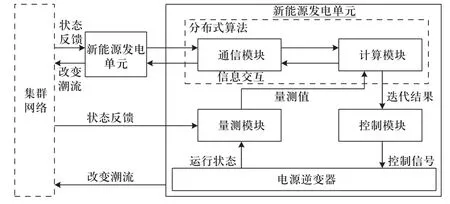
图2 分布式反馈控制架构Fig.2 Framework of distributed control

分布式电压控制的关键在于设计合理的分布式算法，从而计算每步迭代中各电源的无功调整量。本文采用分布式次梯度法进行迭代控制，每步迭代中的控制公式如下：

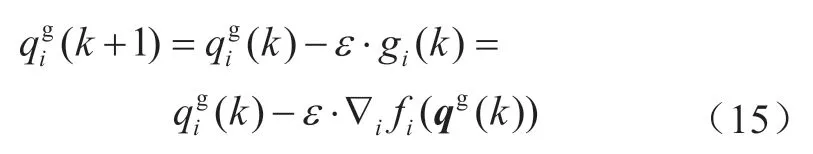
式中：Ni代表与节点i之间具有支路直接相连的节点（包括节点i自身）所构成的集合；Vj(k)代表第k步迭代后节点j的电压幅值。因此，可得本地梯度

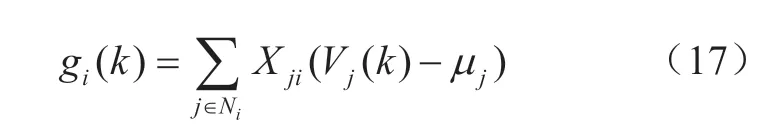
综上所述，式（15）及式（17）即为完整的分布式电压控制迭代公式。不难看出，在每步迭代过程中，节点i电源仅需从全部相邻节点j获取电压幅值Vj(k)，即可完成分布式迭代计算流程。迭代最终收敛时，各新能源发电单元无功注入下，集群电压分布达到最优。由于优化问题形式为盒约束的凸优化，且目标函数需能够拆分成各分布式代理的子目标函数之和，因此根据文献[27]中的证明，其收敛性和最优性可以保证。文献[28]也对类似电压控制模型下采用分布式次梯度及分布式牛顿法的控制收敛性进行了分析和证明。

式（17）的梯度迭代通过电压量测值替代了线性化的无功电压模型关系，因此尽管前述潮流模型推导采用了线性近似，但电压反馈的模式仍可保证电压控制精度不受影响。需要注意的是，上述迭代步骤中尽管无需集中模型维护和求解，但计算本地梯度的式（17）中，节点i电源仍需获取全部相连的支路电抗Xji后方能进行迭代计算，因此分布式方法无法完全脱离线路阻抗参数实现电压控制目标。

在集群配电网中，线路模型参数精确度较差，一旦支路电抗Xji不准确且偏差较大，则可能对分布式迭代收敛速度和电压控制效果产生影响，影响其工程实用性。因此，在第2章中将给出不依赖模型参数的解决方案。

2 基于Koopman的分布式迭代方向校正

2.1 数据驱动的分布式电压控制架构

在第1章中基于模型的分布式电压控制的基础上，为解决该方法仍依赖于模型参数的问题，本文采用基于Koopman方法的数据驱动构建高精度线性潮流模型，并以此推导得出分布式迭代控制中的Xji系数，从而代替第1章中基于模型的Xji获取方式。相比基于阻抗参数的分布迭代方法，由于系数是通过实际运行数据作为样本得到的，控制效果不依赖于模型参数的精度。上述控制架构可划分为两个层级：

1）集群模型训练层：采集各节点功率注入与电压幅值作为样本输入，周期性地离线训练升维线性等效潮流模型，并以此推导计算Xji系数，通过广播通信下发至各新能源发电单元。

2）电源分布迭代层：利用下发的Xji系数，根据本地与相邻节点电压量测，通过分布式次梯度迭代实时控制新能源无功功率，调节集群电压分布，采用循环反馈迭代方式实现电压优化控制目标。

上述数据驱动的分布式电压控制架构如图3所示。集群模型训练层可基于采集的历史样本进行参数计算，且该参数为全局线性结果，并非平衡点线性化的结果，因此在网络拓扑结构不发生明显改变时，训练得到的参数始终适用，进行周期性维护下发即可。电源分布迭代层可根据参数进行全分布式在线迭代。

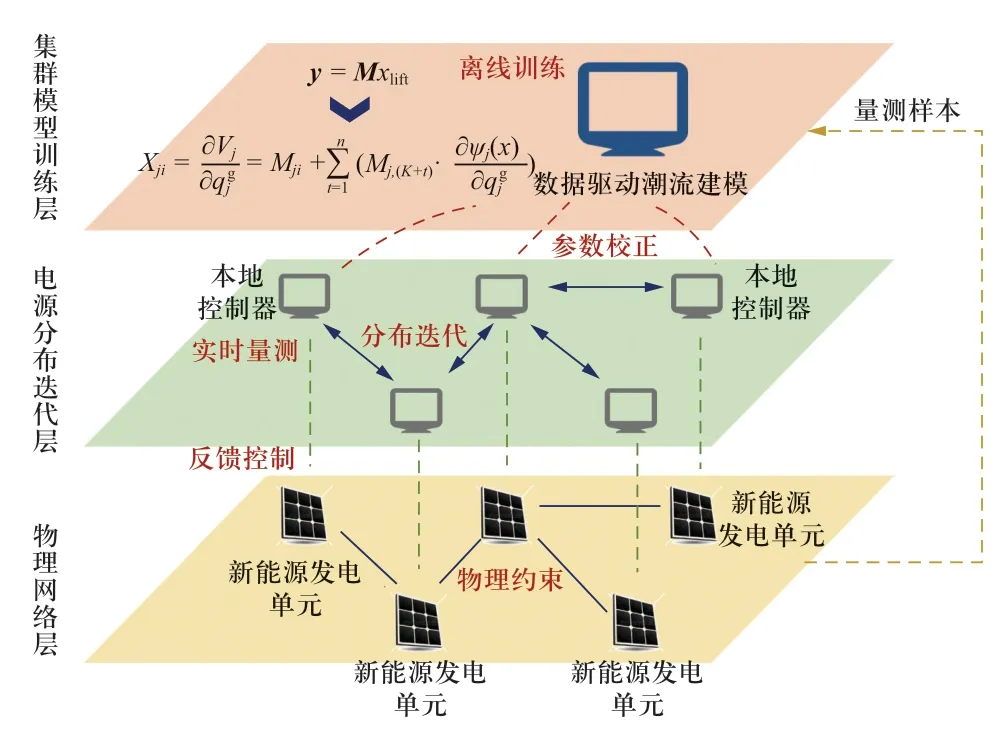
图3 数据驱动的分布式电压控制架构Fig.3 Data-driven distributed voltage control framework

2.2 基于Koopman算子的高维线性化潮流

如前所述，集群潮流模型本质为非线性方程，根据Koopman算子理论，非线性方程可在无穷高维空间中通过线性方程表出，因此基于Koopman方法的潮流建模本质是通过大量实际采集的历史运行数据样本，以数据驱动的方式在升维后的高维空间中，训练得到状态变量与输入变量之间的高维线性关系。具体而言，假设新能源集群满足如下的非线性潮流模型：

式中：状态变量y=[V θ]T由电压幅值与相角构成；输入变量x=[p q]T由有功功率和无功功率构成。

通过对输入变量升维构造线性关系，其本质为坐标系的扩充变换，从而得到全局线性化方程。具体而言，建立升维运算函数ψ(x)，则必然存在线性矩阵M，使得状态变量与输入变量之间满足

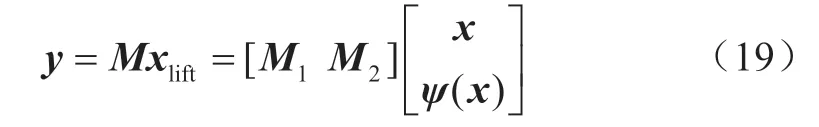
理论上，上述等式仅在升维运算函数ψ(x)为无穷维时方可全局严格成立，但在实际应用中，仅需对输入变量进行一定程度的升维扩充，即可获得较好的线性关系。当升维函数为n维时，其由n个标量函数ψi(x)构成，不同升维函数需要选定不同的基底向量，即

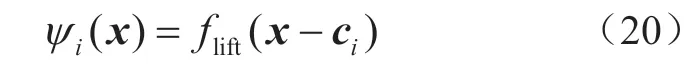
式中：ci为扩充的第i维基底向量，其取值可选择变量范围内的随机值。

升维函数的选择有多种方式，本文采用polyharmonic型升维函数[29]，其表达式为

式中：xi代表x中的第i个元素；cij代表ci中的第j个元素；K为输入变量x的维数。

据此，可根据海量历史样本数据，对线性化矩阵M进行最小二乘估计，得到升维线性潮流方程。假设用于训练的历史样本集共包含S个断面数据，则可定义输入变量样本集X及输出变量样本集Y分别为

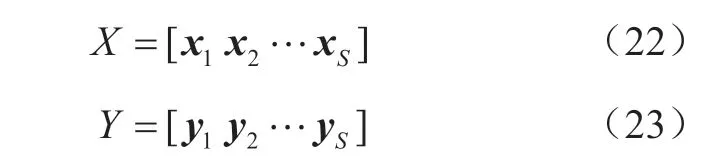
式中：xi和yi分别代表第i个样本断面的输入、输出量测结果。基于上述样本集合，可得线性化矩阵M的估计公式

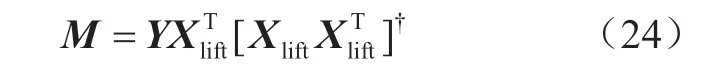
式中：[·]†代表矩阵的Moore-Penrose逆。

根据式（24）计算得到的线性化矩阵M，在集群模型参数未知的情况下，即可描述输出变量y与升维后的输入变量xlift之间的线性潮流关系，得到不依赖于精确参数的潮流方程，且该线性方程并非通过平衡点线性化得到，而是通过升维变换得到的全局线性关系，其优势将在分布迭代中体现。

2.3 基于数据驱动的分布式迭代方向校正

在模型不完备的集群中，通过上述方式可基于历史数据样本得到高精度全局线性化潮流方程。在此基础上，可进一步推导得到式（17）中更为精确的分布式迭代方向，实现模型不完备下的分布式电压控制。

Xji代表节点j电压幅值对节点i无功注入的灵敏度。通过数据驱动得到的全局线性潮流方程，即可计算Xji的精确取值，计算公式如下：

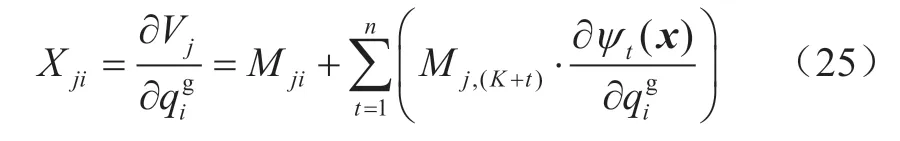
式中：Mji代表线性矩阵M中对应输出变量Vj与输入变量的元素；代表对应输出变量Vj与第t个升维变量ψt(x)的元素，且等式右侧的偏导数可按下式计算：

因此，本地梯度gi(k)的取值可基于离线训练得到的矩阵M、基底向量ci和本地与相邻节点电压量测Vj(k)得到，通过数据驱动方式实现模型不完备情况下分布式迭代方向的校正。

3 算例分析

本章通过算例验证所提出的数据驱动分布式电压控制效果。为了便于效果分析，理想电压幅值μi设定为单位标幺值。本文采用IEEE标准33、69及123节点系统作为基础测试系统，并增加分布式光伏构造高比例新能源发电集群。每个算例系统下均测试4种不同的光伏渗透率场景：10%、15%、20%、30%。

在电压控制过程中，集群参考节点电压V0假设保持为1，全部节点的电压安全范围设定为[0.95,1.05]。电压控制效果的仿真计算通过MATLAB软件实现，其中潮流及电压变化的计算在MATPOWER中完成，并以此作为实际系统运行状态反馈。这种电压反馈模式保证了电压控制的精确性，使得迭代结果足够接近真实最优解。

为训练分布式迭代中的灵敏度参数，本文在每种算例系统的不同渗透率场景下利用MATPOWER各构造3000个运行样本，并通过将输入变量升维至2000维进行数据驱动训练，从而得到各场景下的数据驱动潮流矩阵M。为验证所提出方法的收敛性、最优性及电压控制效果，本文将数据驱动的分布式电压控制结果与基于模型参数的分布式电压控制结果进行对比，并讨论模型参数存在误差（在精准线路电抗参数上添加±（3%～8%）的随机扰动）时的影响。基于模型参数的分布式电压控制采用1.1节中构造的线性化支路潮流方程，以此计算分布式次梯度控制过程中的迭代方向。与此同时，以基于精确模型的集中式内点法计算得到的交流最优潮流作为电压控制问题的最优解。

3.1 正常通信条件下的效果分析

在光伏渗透率为10%的场景下，图4对比了33节点系统中控制前后的电压分布效果。其中蓝色曲线代表本文方法控制下的节点电压分布，红色曲线代表不进行电压控制下的自然电压分布。不难看出，通过分布式电压控制，节点电压分布更为平缓且接近额定电压。电压控制前由于分布式光伏的功率注入，导致部分节点出现电压越限现象，通过采用本文提出方法，电压越限问题得到解决，各节点电压均控制在安全范围内，有效地改善了电压剧烈波动，降低新能源发电的脱网风险。

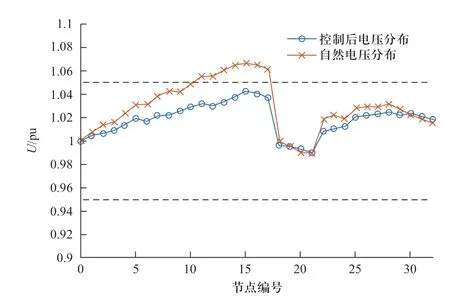
图4 33节点系统电压控制效果Fig.4 Voltage control performance in the 33-bus system

在分布式迭代收敛性方面，图5给出了在33节点系统中光伏渗透率为10%的场景下电压控制目标函数值随分布式迭代步数的变化曲线，其中蓝色曲线为提出的数据驱动分布式电压控制下的目标函数值变化。不难发现，目标函数值在16步迭代内快速下降到最优值附近。如前所述，本方法采用实时电压量测作为反馈，且通过数据驱动方式得到精确迭代方向，因此迭代结果与理论最优值足够接近。

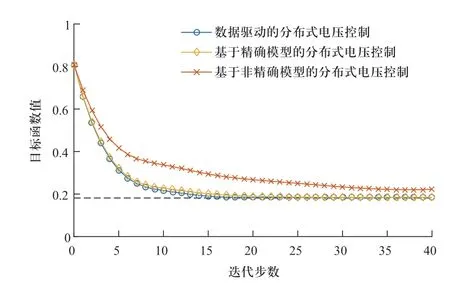
图5 33节点系统中3种方法收敛速度Fig.5 Convergence of 3 methods in the 33-bus system

作为对比，黄色曲线代表基于精确模型参数的分布式控制下的目标函数值变化，而红色曲线代表采用非精确模型参数的分布式控制下的目标函数值变化。由于采用模型参数的方法在推导过程中进行了较多线性近似，收敛速度上相比本文方法稍慢，而基于模型的方法一旦遭遇参数不精确问题，其收敛速度将受到明显影响，限制了分布式电压控制的在线应用，且收敛结果产生偏差，影响电压控制效果。上述对比验证了本文所提出的方法在模型不完备场景下的显著优势。

为更好地验证不同方法间的效果差异，进一步给出同样在光伏渗透率10%场景下69节点系统和123节点系统目标函数值的变化曲线。图6给出了69节点系统中3种不同方法下目标函数值随迭代步数的变化结果，可见通过数据驱动方法修正迭代方向的方法在54步迭代后收敛到最优值附近，而基于精确和非精确模型参数的迭代则分别需要68步和197步达到收敛。图7给出了123节点系统中3种不同方法下目标函数值随迭代步数的变化结果，可见本文方法目标函数值在133步迭代内下降到最优值附近，而基于模型的方法则分别需要168和392步迭代达到收敛。因此，在不同规模系统下，均验证了本文方法相比依赖于模型参数的分布式电压控制的显著优势。

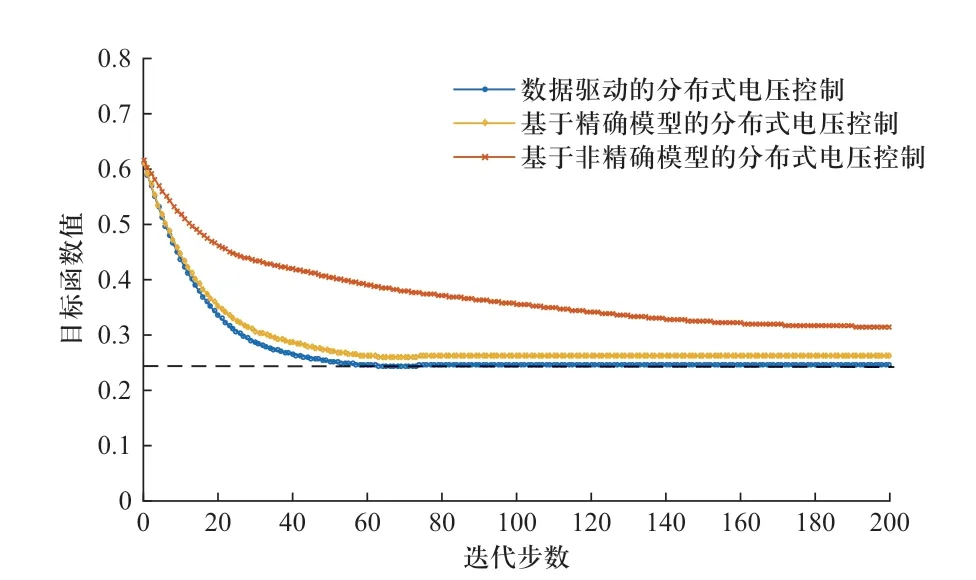
图6 69节点系统中3种方法收敛速度Fig.6 Convergence of 3 methods in the 69-bus system

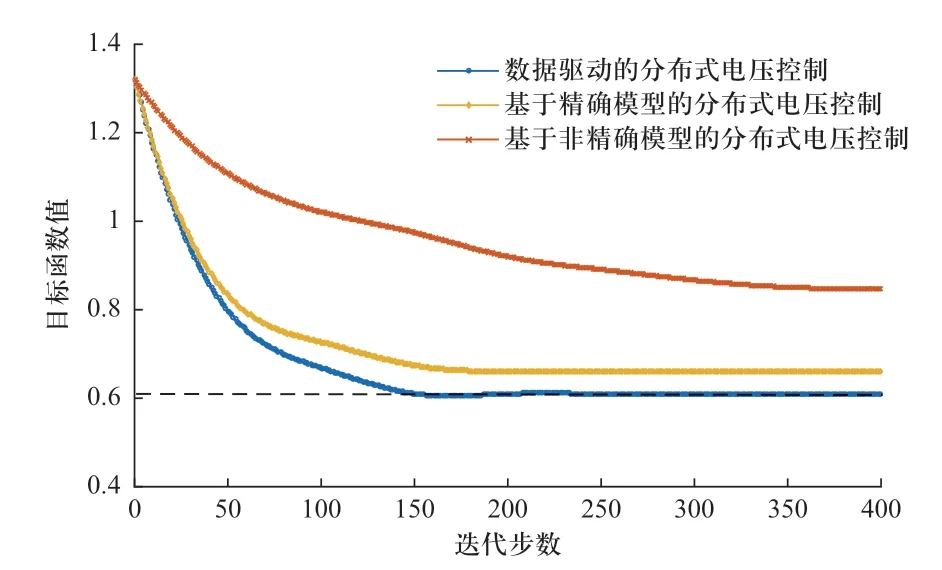
图7 123节点系统中3种方法收敛速度Fig.7 Convergence of 3 methods in the 123-bus system

表1—表3分别给出了4种不同渗透率下在33节点、69节点和123节点系统中3种方法达到收敛所需的迭代步数。可以看出，在总共12种场景下，基于数据驱动的分布式电压控制均以最快的速度实现收敛，特别是在参数不精确场景下，本文方法相比基于参数的迭代无论收敛性和最优值均有显著优势。随着系统节点规模的增加，本文方法收敛性的优势更加明显，因此更适用于海量新能源接入的高比例发电集群电压控制。

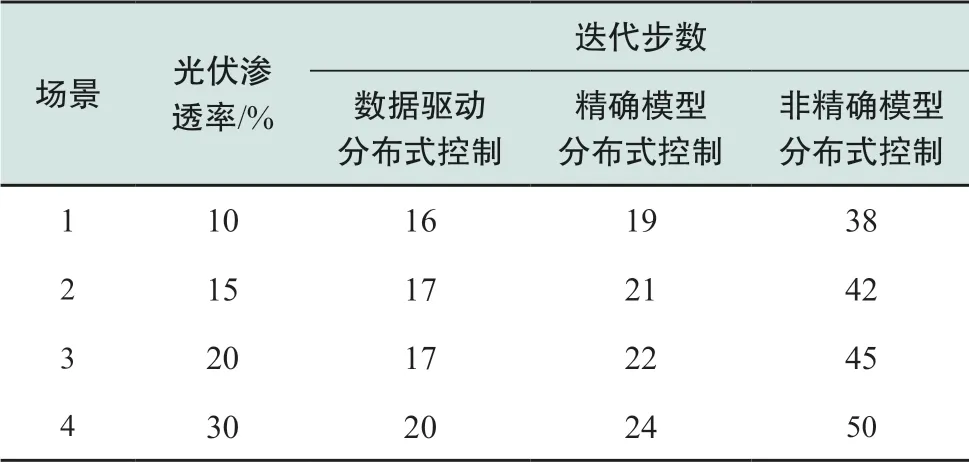
表1 33节点系统收敛性对比Table 1 Comparison of convergence in the 33-bus system

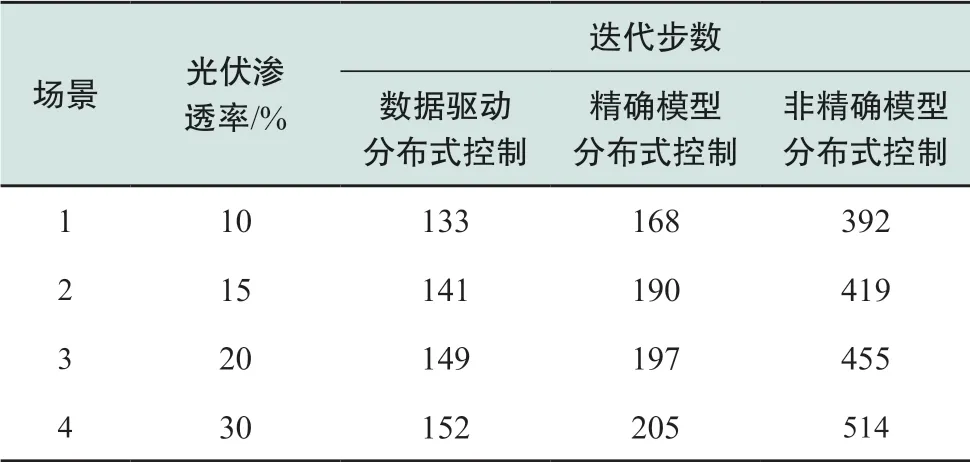
表3 123节点系统收敛性对比Table 3 Comparison of convergence in the 123-bus system

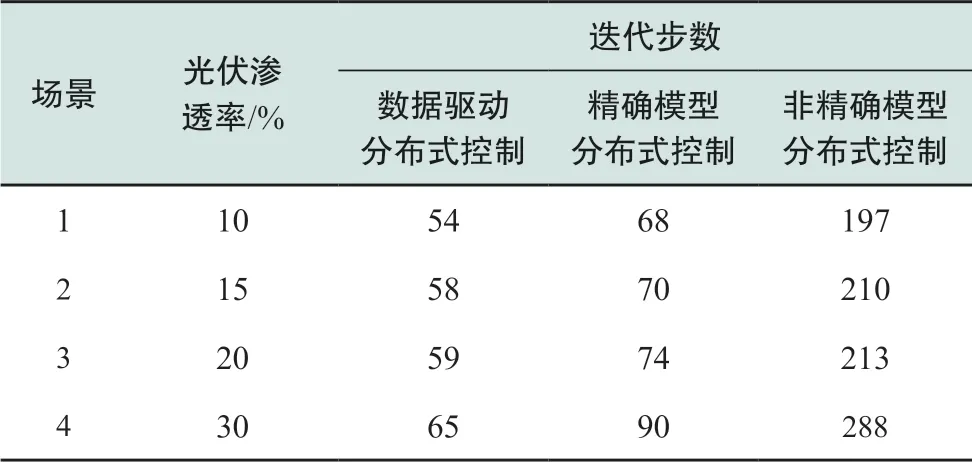
表2 69节点系统收敛性对比Table 2 Comparison of convergence in the 69-bus system

3.2 通信故障条件下的效果分析

相比集中求解电压优化问题，分布式反馈控制的优势在于跟踪电压变化的响应速度更快，且发生单点通信故障导致全局崩溃的风险降低。然而，即使在分布式点对点通信条件下，仍有可能发生因通信系统问题导致全部通信中断的风险。因此，有必要对失去通信条件下的分布式控制效果进行分析。

从式（17）中可以发现，当相邻节点的电压量测无法通过通信获取时，分布式控制退化为仅依靠本地电压幅值量测Vi(k)及数据驱动灵敏度Xii进行梯度和迭代方向计算的方法，可视为改进的下垂控制策略。

为验证失去通信后采用数据驱动迭代方法的效果，采用安徽某区域实际量测的日光照变化值作为输入，图8给出了10%光伏渗透率下33节点系统中6号节点电压在正常情况和通信故障下的电压日波动曲线。可以看到，在进行电压控制前，由于午间光伏出力导致6号节点电压出现越限情况，而通过分布式电压控制，节点日电压变化全部控制在安全范围内。即使在通信全部失去的场景下，通过数据驱动方法训练得到的本地迭代方向，仍能够保证电压不越限，且与正常情况下的电压控制效果相比较为接近。这一结果验证了本文方法在通信故障条件下的适应性，在实际工程中具有较好的应用价值。

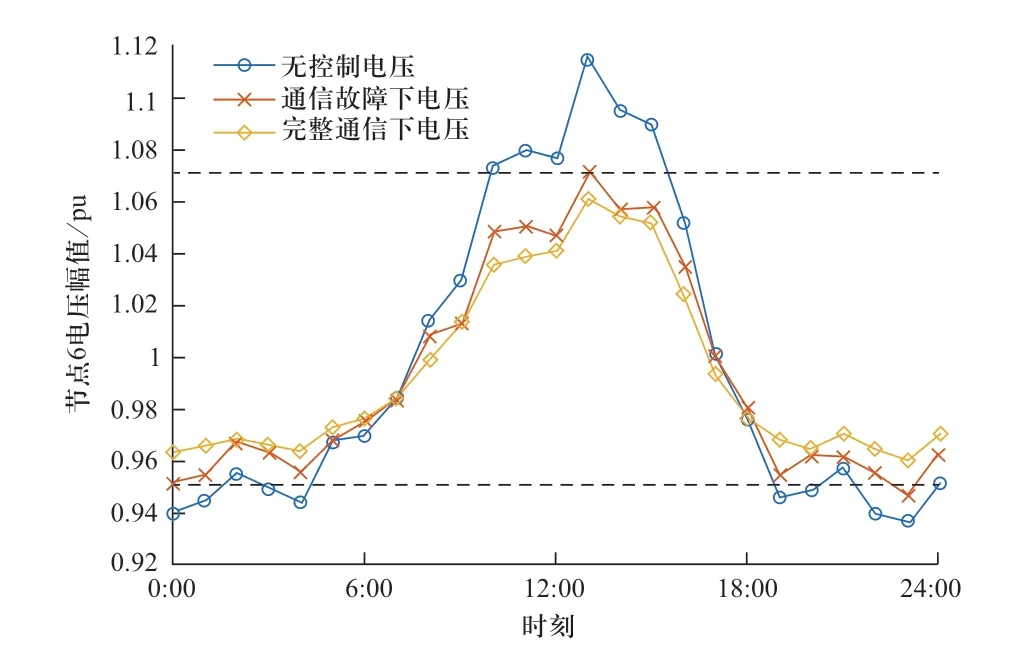
图8 33节点系统6号节点电压日变化曲线Fig.8 Daily voltage variation of bus 6 in the 33-bus system

4 结论

新能源发电集群模型参数精度问题制约传统基于模型的新能源发电集群电压控制方法效果。已有的分布式电压控制研究虽然能够解决单点故障的问题，但仍需依赖线路参数确定迭代方向。本文提出了一种基于数据驱动的高比例新能源发电集群分布式电压控制方法。在集群层面，基于集群海量运行数据采集，通过Koopman方法对非线性潮流方程进行高维线性等值，离线获取不依赖于集群模型参数的高精度无功-电压灵敏度数值，并周期性下发至新能源发电单元。在新能源发电层，基于数据驱动获取的灵敏度修正分布式次梯度迭代方向，实现新能源发电集群实时分布式高效迭代电压控制。算例分析表明，所提出的数据驱动分布式电压控制能够改善集群电压分布并实现最优无功分配，且在模型不精确场景下，在迭代收敛速度和电压控制结果方面本文方法相比传统基于模型参数的分布式优化方法具有显著优势。在通信故障条件下，本文方法依然具有较强的适应性，在实际工程条件下具有较好的应用价值。