基于数据拟合的配电网线性运行约束建模方法
2022-05-19杜嫣然杨帆王颖许寅
杜嫣然,杨帆,王颖*,许寅
(1.北京交通大学电气工程学院,北京市 海淀区 100044;2.北京电力经济技术研究院有限公司,北京市 西城区 100055)
0 引言
配电网的稳态运行需要满足一系列运行条件,这些条件通常作为运行约束在配电网优化问题中予以考虑,如配电网优化运行问题和故障恢复问题等。具体来说,配电网稳态运行约束包括潮流约束、节点电压限制约束、线路电流限制约束等。其中,后两种约束均可建模为线性约束,而潮流约束为非线性等式约束,属于非凸约束,在优化问题中较难处理。
针对上述问题,大量学者对于潮流方程在配电网优化问题中的处理方式开展了一系列研究,并取得了诸多富有价值的研究成果。总体来说,相关处理方法主要有三类,包括启发式/元启发式方法、基于神经网络的方法以及数学规划方法。其中启发式/元启发式方法主要通过提出某些基于启发式思想的规则或智能算法等随机择优机制,确定部分变量的值,再用潮流校验的方式进行验证,具有运算速度快的优点,但难以保证全局最优解[1-6]。基于神经网络的方法主要通过训练神经网络来建立节点电压与注入功率的关系,当选择的神经网络模型为凸时,则最终构成的优化问题为凸优化问题[7-8],具有一定参考价值。但此种方法对神经网络及其训练过程涉及的各种参数具有较高要求,且实用性有待验证。数学规划方法的主要思想是将潮流方程进行凸松弛或基于某些假设进行线性化处理[9-29],将原问题转化为连续凸优化问题,如线性规划(linear program,LP)[9-10]、半定规划(semidefinite program,SDP)[11-13]、二阶锥规划(second order cone program,SOCP)[13-14];或转化为混合整数优化问题,如混合整数线性规划(mixed-integer linear program,MILP)[15-17]、混合整数二阶锥规划(mixedinteger second order cone program,MISOCP)[18-20]或混合整数半定规划(mixed-integer semi-definite program,MISDP)[20],利用成熟的优化求解器进行求解,近年来取得了一系列成果。其中,采用凸松弛手段将潮流约束松弛为半定约束或二阶锥约束,若得到的解不满足松弛前的约束,则该解无意义;此外,由于该类约束仍为非线性约束,将其应用于恢复问题等混合整数优化问题时,可能导致求解速度过慢难以满足在线应用需求的问题[13]。因此,诸多学者将潮流方程进行线性化处理,并取得了一定进展,主要分为两类解决思路。一类是根据潮流方程的特点,基于一定的假设对其线性化[10-11,21-23]。其中,基于线路损耗较小、系统中节点各相电压平衡的假设,文献[11]提出了一种忽略网损的经典线性潮流模型(linear power flow,LPF),该模型潮流计算误差满足实际应用,并在不同的优化场景下得到了广泛的准确性与计算效率的验证[24-27]。可见将潮流线性化是高效解决优化运行问题的良策。但该模型没有考虑电流,且会因未考虑网损而导致在某些场景下求解结果不可行的问题[15-17]。另一类思路是基于数据拟合的方法将潮流方程线性化[28-29],但尚未发现将其用于优化问题建模方面的相关研究。
综上,现有配电网运行约束模型存在一定的难以兼顾求解效率与模型精度的问题[30-33]。因此,本文基于数据拟合的方法,针对三相不对称配电网,构建了配电网运行约束的线性模型,并将其应用于配电网优化运行与故障恢复问题,并在多个算例中验证所提模型的有效性和优越性。
1 基于数据拟合的运行约束建模方法
潮流方程中涉及的主要状态参量包含节点电压、线路电流与节点注入功率。根据文献[34],对于在正常运行范围内的配电系统,即整体节点电压在0.9~1.1 pu间且负荷未过度超载的情况下,各状态参量间的关系近似线性。本节以该文献对潮流方程涉及的状态参量间线性程度的分析结果为基础,建立基于数据拟合的线性运行约束模型。模型建立过程如图1所示。
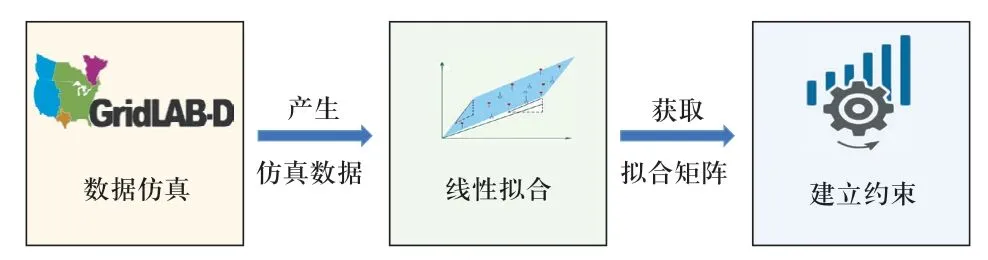
图1 基于数据拟合的运行约束建立过程Fig.1 Procedure of establishing operation constraints based on data fitting
1.1 数据仿真
本文利用配电系统仿真软件GridLAB-D[35]产生模型拟合所需的数据组。首先根据配电系统的网架参数和拓扑信息建立仿真模型,然后按照正态分布调节系统各节点负荷量。考虑到新能源的接入以及负荷日常波动对电网运行所带来的不确定性,在配电系统节点电压处于0.9~1.1 pu范围内的情况下进行仿真,仿真数据集包含了配电网运行可能出现的多种运行情况,最终产生大量关于配电系统各节点电压、线路电流和节点注入功率的仿真数据组。
1.2 线性拟合
在配电网潮流方程中,线路和设备阻抗等静态参数为常数,主要状态变量为节点电压和支路电流,主要输入变量为节点注入功率。对于(n+1)节点(包含一个平衡节点)辐射状配电网,基于多元线性回归方法,利用丰富的仿真数据,建立配电网节点注入功率平衡关系及其与节点电压和线路电流的最优线性映射,能够简化原潮流模型中数据间的非线性关系。可以拟合绝对误差的平方最小化为目标,获得所述状态参量间的近似线性关系。即根据大量仿真数据组,以式(1)为目标,求解优化问题:
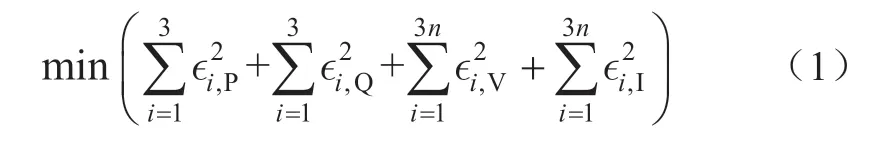

式中:∊i表示绝对误差;表示近似模型计算得到的估计值,其计算方式如式(3)所示;表示真实值或准确模型计算值。

其中:式(4)表示各节点注入功率平衡关系;式(5)和式(6)分别表示电压和电流随注入功率的线性变化关系。以上约束共同构成了基于数据拟合的线性潮流模型(fitting linear power flow,FLPF)。
1.3 线性运行约束模型
根据上述方法,利用大量的仿真数据,基于线性回归,通过优化算法可得到注入功率线性平衡关系及其与节点电压和线路电流的线性关系矩阵。对应安全运行约束如下:


式(7)表示配电网各相有功、无功功率平衡约束,式(8)表示节点电压约束,式(9)表示线路电流极限约束,式(10)表示电源出力极限约束。以上约束共同构成基于线性拟合模型的配电网优化运行约束。
2 含线性运行约束的配电网优化模型
2.1 配电系统优化运行问题
2.1.1 目标函数
配电系统运行优化问题亦可称为最优潮流问题(optimal power flow,OPF),一般以网损最小为目标函数,考虑到配电网电压问题也较为突出,因此某些研究在进行配电网运行优化时以整体电压偏移最小为目标[36]。本文分别就这两种情况展开讨论。
1)网损最小。配电网运行经济性对应目标函数如式(11)所示:

式中:Pi是所有节点各相有功注入功率向量(PG—PL)中的元素,维度为3(n+1)。
2)整体电压偏移最小。配电系统整体电压偏移最小目标函数可以建模如下:
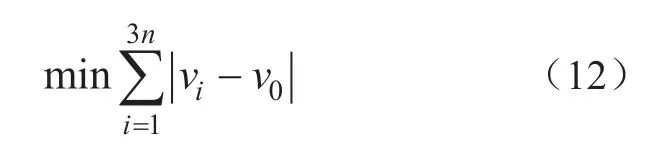
式中:vi为各节点各相电压幅值;v0为基准电压值。
2.1.2 约束条件
根据上一节数据拟合的线性建模方法,可得到注入功率与节点电压、线路电流、平衡节点功率的线性关系矩阵。配电网最小网损模型和最小电压偏移模型的约束条件主要包括潮流约束、节点电压越限、节点电流极限约束以及各分布式电源出力约束,约束形式与式(7)至式(10)相同。
对于最小电压偏移问题,根据目标函数引入的电压变量vi增补等式约束如下:

式中:V表示维度为3n的待决策节点电压变量,vi为其中的元素。
综上,建立了配电网优化运行问题的两个优化模型,均为基于数据拟合的线性规划模型(fitting-linear program,F-LP)。
2.2 配电系统故障恢复问题
本文关注的配电系统故障恢复问题是面向大停电场景下利用配电网本地电源实现重要负荷优先恢复的问题[18]。考虑到配电网的联络开关个数有限,配电网潜在的运行结构种类为有限个数,通过离线仿真能够针对不同的运行状态拟合出相应的潮流矩阵系数。本文要解决的恢复问题旨在确定恢复策略,即恢复后线路状态(拓扑)、负荷恢复状态(恢复哪些负荷)和电源出力(系统运行点),并不解决恢复操作次序问题,也不考虑拓扑改变问题。因此,基于团队前期成果,可首先确定恢复所形成的孤岛系统最优拓扑结构[37],即重构方案;然后,利用下文所建立的恢复模型确定可恢复的重要负荷集合。
2.2.1 目标函数
故障恢复模型以最大化加权负荷恢复数目为目标:

式中:ω为已知常量,表示负荷权重系数构成的向量;r为各个负荷恢复状态构成的向量,内部元素为0-1整数变量。
2.2.2 约束条件
根据建立的基于数据拟合的运行约束模型,故障恢复问题的优化约束形式如下:

式(15)表示配电网各相有功、无功功率平衡,式(16)表示节点电压约束,式(17)表示线路电流极限约束,式(18)表示发电机出力限制约束。
在上述故障恢复模型中,决策变量包含整数变量,目标函数和约束条件均是线性的,因此该模型为基于数据驱动的混合整数线性规划模型(fitting-mixed integer linear program,F-MILP)。
3 算例测试
本文分别对所提出的基于数据拟合的线性潮流模型及含所提运行约束的两类优化模型在三相不对称配电网系统中进行算例测试。在线性潮流模型准确性测试中,以利用仿真软件得到的结果为基准参照数据。在配电系统优化模型测试中,对于OPF问题,以SDP模型[13]计算结果为基准;对于故障恢复问题,以MISDP[20]求解结果为基准。利用Julia语言进行编程,利用成熟的求解器Mosek和Gurobi求解优化模型。所有测试均在配置为Intel Core i5中央处理器、主频1.6 GHz、运行内存16 GB 的台式机上进行。
3.1 基于数据拟合的线性潮流模型准确性测试
针对IEEE 13、34、37、123节点三相不对称配电网标准算例,以各算例的GridLAB-D仿真潮流结果为基准,根据式(2)绝对误差的计算公式,计算了基于本文提出的FLPF模型的电压、电流的拟合绝对误差,同时利用文献[11]提出的经典线性潮流模型LPF计算得到电压及误差,测试结果如表1所示。
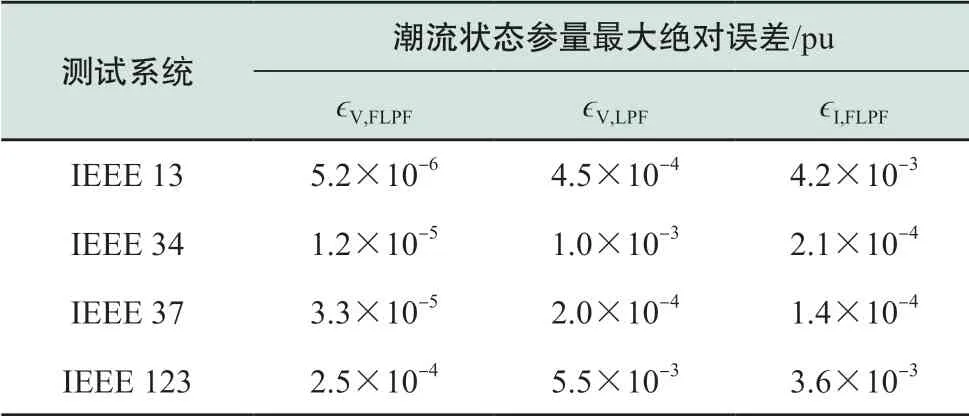
表1 两潮流模型在不同测试系统下最大计算绝对误差Table 1 Maximum absolute error of different test feeders in two power flow models
如表1所示,本文提出的FLPF模型的节点电压和线路电流的线性拟合最大绝对误差较小,满足优化应用需求;对比两模型中电压结果的绝对误差,本文模型误差更小、模型精度更高;由于LPF模型中未考虑电流量,并未列出对比。综上,本文拟合的线性潮流模型相比LPF更为精确。
3.2 配电系统优化问题测试结果
1)以网损最小为目标的OPF问题。
在IEEE 13节点标准算例的基础上,分别在节点3、节点8和节点11处配置了3个分布式电源,如图2所示。
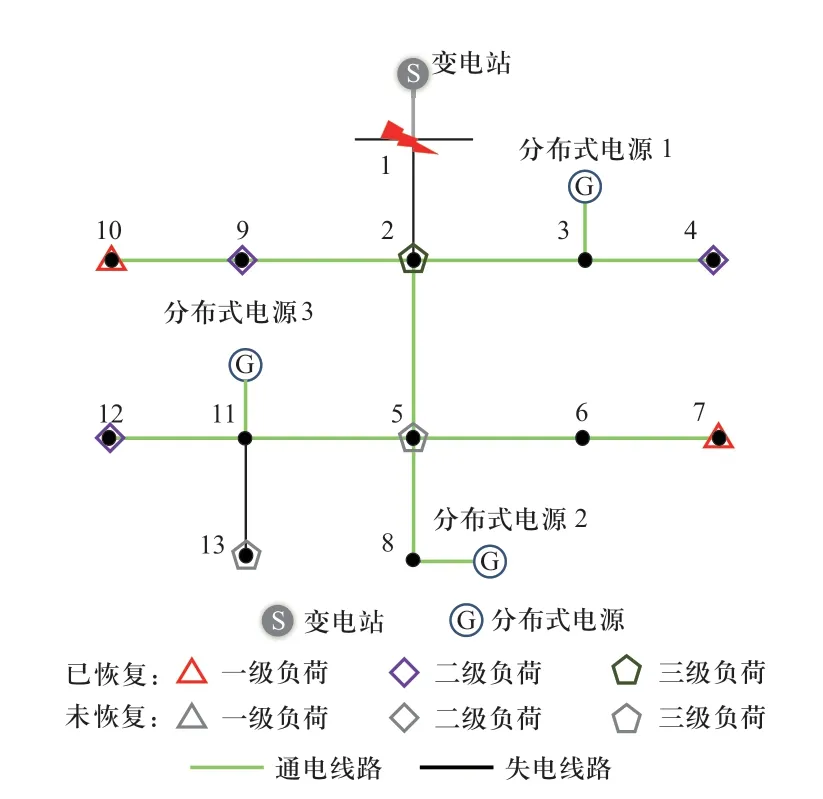
图2 修改后的IEEE 13节点算例故障恢复结果Fig.2 Restoration results of the modified IEEE 13-bus system
各分布式电源的额定有功功率分别为400 kW、500 kW和860 kW,额定无功功率分别为240 kvar、320 kvar和550 kvar。针对修改后的IEEE 13节点算例,测试结果如表2所示。
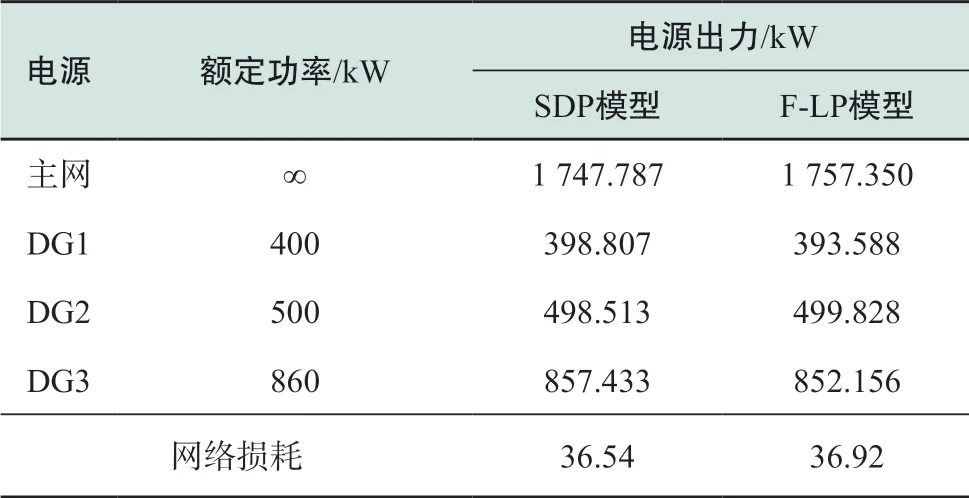
表2 修改后的IEEE 13节点系统最小网损优化结果Table 2 Optimization results of minimum power loss problem for modified IEEE 13-bus system
从表2可以看出,SDP模型与F-LP模型的电源出力数值近似,误差不超过1.3%,验证了本文所提出的基于线性拟合的规划模型的准确性。
2)以电压偏移最小为目标的OPF问题。
针对修改后的IEEE 13节点算例,以电压偏移最小为目标,分别利用本文提出的F-LP模型与SDP模型进行求解,各节点各相电压幅值的计算结果如图3所示。
从图3可以看出,两个模型所得的电压幅值曲线相似度很高,三相电压最大绝对误差为0.000 82 pu,验证了本文提出优化模型的准确性。
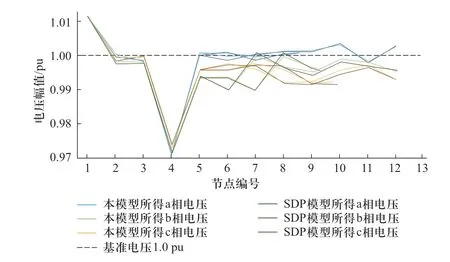
图3 修改后的IEEE 13节点系统电压分布Fig.3 Voltage profiles of the modified IEEE 13-bus system
3)故障恢复问题。
基于修改后的IEEE 13节点配电网算例校验本文提出的F-MILP模型的准确性。依据负荷等级规范,将负荷分为一级负荷、二级负荷和三级负荷3个等级,各等级负荷的权重系数分别为10、1和0.1。假设极端事件导致配电网无法从上级电网获取电能,各节点电压上下限为0.95~1.05 pu。本算例共有2个一级负荷,3个二级负荷和3个三级负荷。恢复结果如图2所示。
结果中,F-MILP模型与MISDP模型优化求解得到的加权负荷恢复数均为23.1。一级负荷和二级负荷全部被恢复,还有1个三级负荷被恢复,两模型的恢复结果相同,验证了本文模型的准确性。
3.3 与经典线性模型LPF对比测试结果
3.3.1 OPF问题
针对修改后的IEEE 13、34、37、123节点三相不对称配电网算例,分别以最小网络损耗和最小电压偏移为目标,利用SDP模型、基于LPF的LP模型以及本文提出的F-LP模型进行了测试和对比。修改后的IEEE 34、37和123节点算例新增分布式电源信息见附录A。利用加速比k来对比模型的计算速度:

式中:to表示基准模型计算时间;tm表示新模型计算时间。
1)以网损最小为目标的OPF问题。
由于LP模型并没有考虑网损,因此无法求解以网损最小为目标的OPF问题。F-LP和SDP两个模型的测试结果如表3所示。
如表3所示,对比优化结果,在不同规模的标准算例下最小网损优化结果几乎一致,体现了本文所提线性模型的准确性;在计算时间方面,测试的所有系统中,本文提出的F-LP模型的计算速度都优于SDP模型;另外,随着系统规模的不断扩大,加速比增大,本文提出模型的计算速度优势越明显。
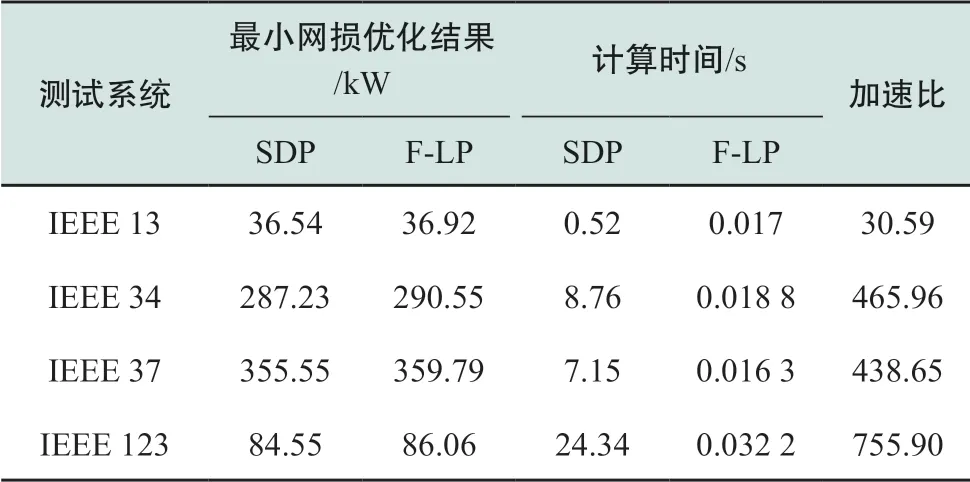
表3 不同测试系统最小网损优化结果Table 3 Optimization results of minimum power loss problem for different test feeders
2)以电压偏移最小为目标的OPF问题。
对于最小电压偏移问题,以SDP模型求解所得到的各节点电压为基准,对比本文模型与基于LPF的LP模型各节点电压的最大绝对误差,算例测试结果如表4所示。
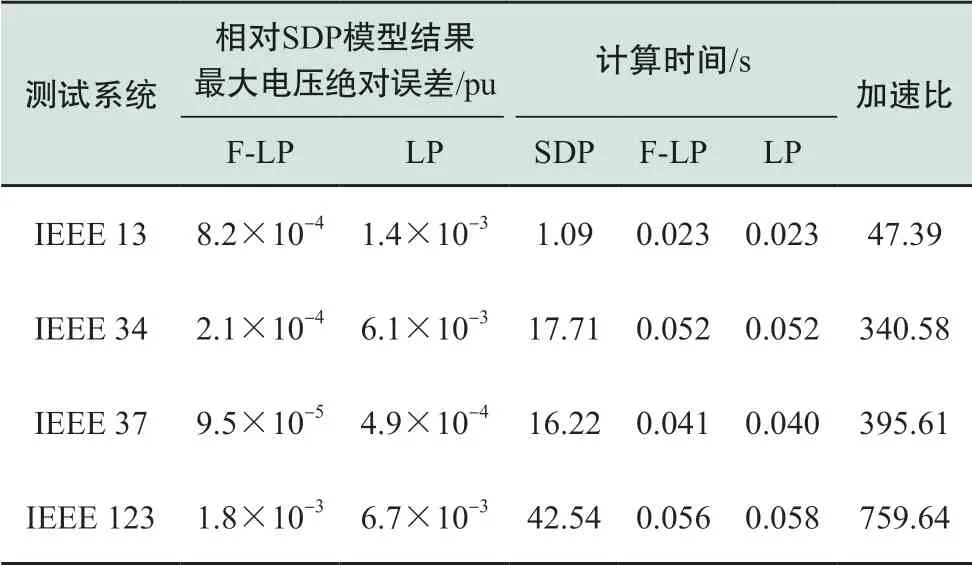
表4 不同测试系统最大电压绝对误差Table 4 Maximum absolute error of voltage for different test feeders
如表4所示,在不同规模的标准算例下,对于最小电压偏移问题,本文模型相比基于LPF的经典LP模型更准确,两模型计算时间近似。可以看出,随着算例规模的扩大,加速比增大,本文模型的计算速度不断提升;在较大规模的算例中,计算速度相比于SDP模型高出约两个数量级。
3.3.2 故障恢复问题
针对修改后的IEEE 13、34、37、123节点三相不对称配电网算例,利用MISDP模型、基于LPF的MILP模型以及本文提出的F-MILP模型进行恢复策略的求解并进行对比。故障恢复测试结果如表5所示。
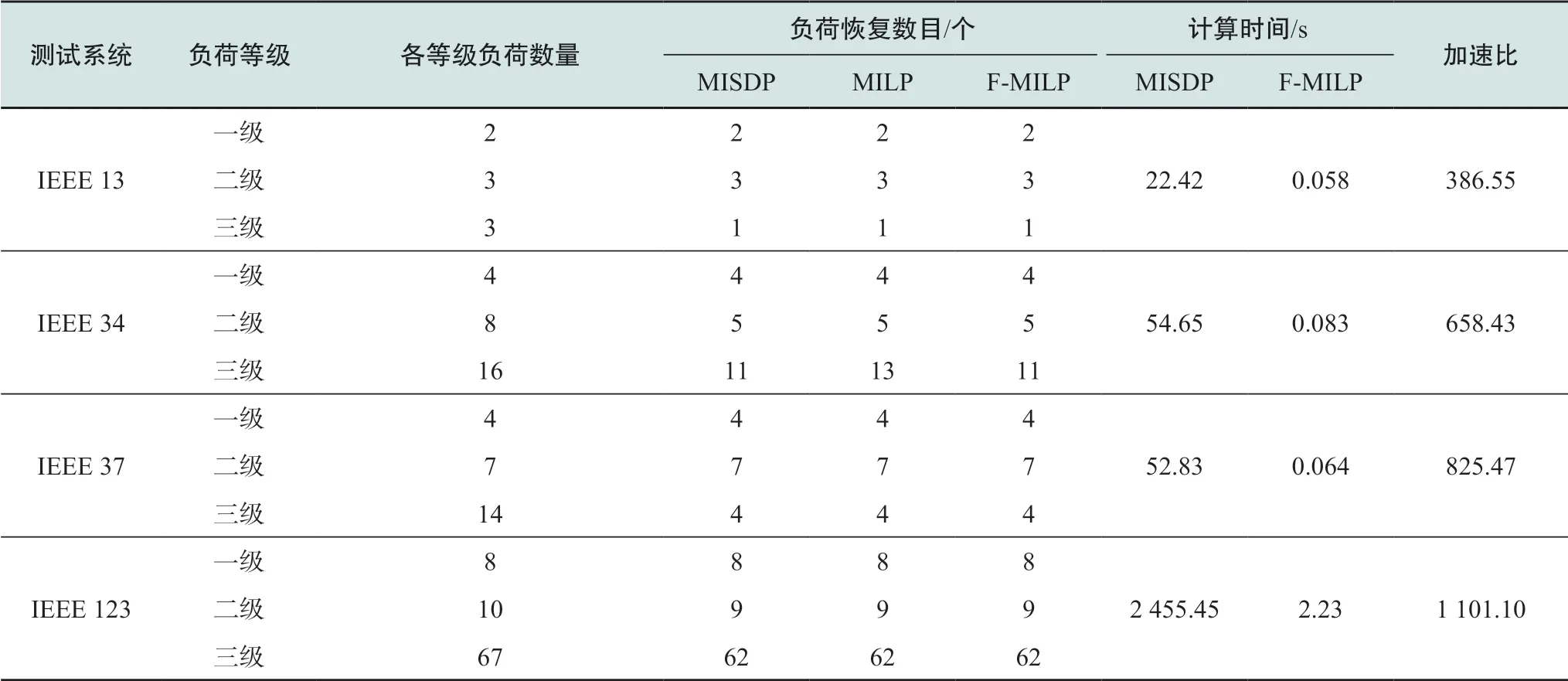
表5 不同测试系统恢复结果Table 5 Restoration results for different test feeders
根据表中的结果可以得出,本文模型与MISDP模型在所有算例中得到的恢复策略结果相同;而MILP模型在IEEE 34配电系统中多恢复了2个三级负荷,此时恢复结果是不可行的。究其原因,IEEE 34节点算例的网损较大且存在负荷需求较小的三级负荷,因此忽略网损会影响测试结果的准确性,而本文模型在拟合过程中考虑了网损,因此与MISDP模型确定的恢复结果相同。进一步,改变分布式电源的位置和容量大小,在5000个场景下对IEEE 13节点算例进行了故障恢复测试,在所有场景下本文模型与MISDP模型的恢复结果都一致,在3.61%的场景下MILP模型会过于乐观地估计恢复结果,即会恢复更多的负荷。观察模型的计算时间可以发现,一方面,MISDP模型的计算效率在所测试的所有算例中均低于本文提出的F-MILP模型;另一方面,随着算例规模的扩大,F-MILP模型的计算效率优势更加明显。
4 结语
本文针对配电网优化中含三相不对称潮流方程的运行约束难以处理且难以兼顾求解效率和模型精度的问题,提出了基于数据拟合的配电网线性运行约束建模方法,并建立了关于配电网优化运行问题的线性规划模型F-LP和配电网故障恢复问题的混合整数线性规划模型F-MILP。测试结果表明,本文提出的F-LP模型和F-MILP模型相比于基于凸松弛潮流约束建立的SDP模型和MISDP模型,求解结果误差小,求解速度优势大,且随着算例规模的扩大,本文模型的计算效率优势更加明显。此外,本文模型求解结果相较于以经典线性潮流LPF为基础的配电网优化模型更为准确,尤其是对于故障恢复问题,可较好地规避乐观估计网损造成的优化结果不可行的问题。未来,拟基于数据拟合方法,进一步探索可以灵活应对拓扑变化的线性运行约束,并将其应用于故障恢复等配电网优化问题中。
附录A 修改后的IEEE 34、37和123节点三相不对称配电系统分布式电源参数
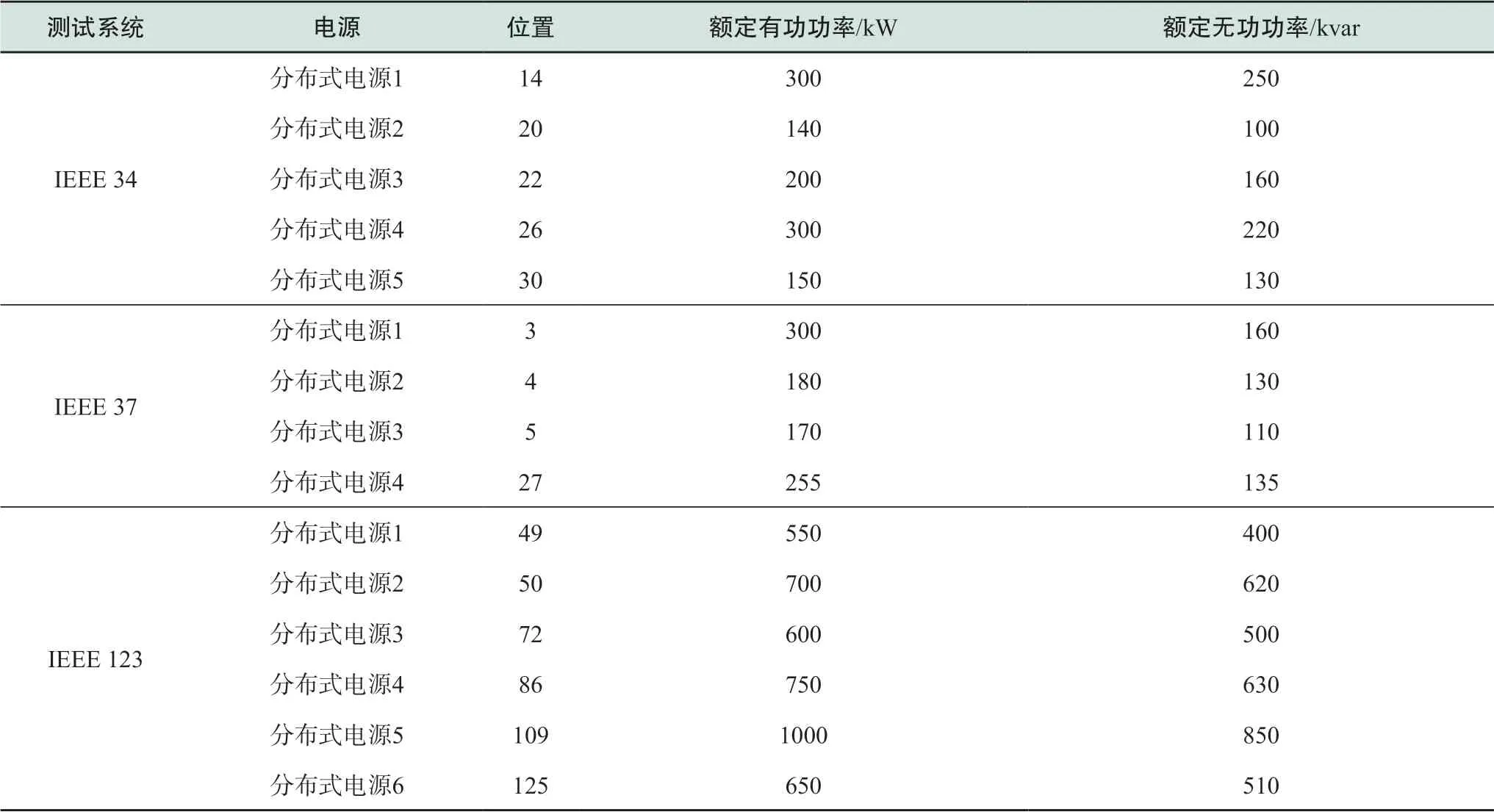
表A1 修改后的IEEE 34、37和123节点三相不对称配电系统分布式电源参数Table A1 Parameters of distributed generations for modified IEEE 34,37,and 123 unbalanced test feeders
