考虑稀薄气体有效黏度的微轴承弹流润滑研究*
2022-05-19郗文君杨利花张彩丽曹巨江
吴 垚 郗文君 杨利花 张彩丽 曹巨江 王 哲
(1.陕西科技大学机电工程学院 陕西西安 710021;2.西安交通大学航天航空学院 陕西西安 710049;3.施耐德(西安)创新技术有限公司低压事业部 陕西西安 710075;4.西安工程大学材料工程学院 陕西西安 710048)
随着微型燃气轮机、微电机、超精密机床主轴、谐振滤波器和惯性导航系统等具有高能量密度和高功率密度的微动力机电系统(micro-electromechanical systems,MEMS)和微流体器件的快速发展,微气体滑动轴承因其结构简单、高转速、高精度、低功耗、低摩擦特性以及工作温度范围宽等优点在微旋转机械领域中被广泛应用[1-3]。传统轴承设计中通常假设滑动轴承轴瓦为刚性且润滑剂黏度保持不变。而微型轴承由于气膜厚度和特征尺度较小,轴瓦弹性变形会显著改变轴承表面几何形状甚至与初始轴承间隙达到相同数量级;此外,根据VEIJOLA和TUROWSKI[4]的有效黏度模型,可压缩润滑剂黏度是Knudsen数的函数,而Knudsen数是表征气体稀薄程度的参数,定义为气体分子平均自由程与微通道内气体流动特征长度的比值[5]。因此,刚性体和常黏度润滑剂假设在超薄气膜润滑计算中将不再适用,非常有必要分析轴瓦弹性变形和黏度变化对稀薄气体润滑性能的影响,为提高微气体轴承-转子系统的稳定性提供理论依据。
近几十年来,国内外学者关于超薄气膜润滑技术已开展了许多卓有成效的研究并取得了一些重要成果。其中,BURGDORFER[6]、HSIA和DOMOTO[7]、MITSUYA[8]、FUKUI和KANEKO[9-11]、BAHUKUDUMBI、BESKOK[12]分别提出了不同的泊肃叶流流量模型,推导了相应的修正Reynolds方程,研究了气体稀薄效应对轴承性能的影响。由于在求解磁头/磁盘的超薄气膜润滑性能时轴承数很大且剪切流项含有压力,黄平和牛荣军等[13-14]提出了求解大轴承数气体润滑Reynolds方程的有效有限差分算法。ZHANG等[15]利用有限体积法和原子力显微镜数据研究了随机粗糙表面对气体微型轴承流动特性的影响,计算表明分形表面的粗糙指数越大,壁面气体滑移速度变化越大。YANG等[16]通过13矩方程将滑移系数视为壁面适应系数和Knudsen数的函数,推导出了新的滑移速度边界条件。ZHANG等[17]耦合Greenwood-Williamson模型和修正Reynolds方程计算了不同槽深和粗糙峰高度标准差的气体螺旋槽推力微型轴承的轴承力和粗糙面接触力。关于轴承弹流润滑分析,在DOWSON和HIGGINSON[18]首次求解等温条件下受重载弹性圆柱体弹流润滑问题后,弹性流体动力润滑理论得到了长足的发展。近年来,YAGI和SUGIMURA[19]对一维固定滑动面轴承的弹流动压润滑性能进行了数值仿真,结果发现小于100 nm的弹性变形对薄膜动压润滑的承载力有明显影响,润滑薄膜形状有从入口出现的恒定薄膜厚度区、位于中心的略微增加区和出口周围的收敛区3个区域。肖乾等人[20]应用COMSOL Multiphysics软件建立了考虑弹性变形和黏压、黏温效应的止推轴承有限元模型,仿真结果表明载荷增大使承载瓦上产生较大变形且油膜压力峰值向出口移动。SUN等[21]研究了轴颈偏斜、表面粗糙度、黏压效应以及弹性变形对径向滑动轴承性能的影响,结果表明轴承表面弹性变形时,表面粗糙度对油润滑偏斜轴承有轻微影响且轴承偏心率越大,轴瓦变形对轴承特性影响越明显。LINJAMAA等[22]考虑了轴承表面的弹性变形和热变形,建立了含有柔性聚合物的动静压径向滑动轴承参数化计算模型,该模型评价了包括轴颈偏斜等不同运行条件下主要轴承性能参数。根据湍流润滑理论,CHETTI[23]推导了考虑湍流状态、耦合应力流体和弹性变形影响的修正Reynolds方程,得到了不同耦合应力系数、弹性系数和Reynolds数下的承载力、偏位角、摩擦因数以及端泄量(side leakage),结果表明耦合应力流体提高了刚性和弹性滑动轴承在层流和湍流状态下的稳态性能。
综上所述,已有的文献对微型气体轴承弹性流体动力润滑性能的研究较少。另外,由于微型动压轴承复杂的气弹耦合行为,在求解微型轴承微观弹流润滑问题时,需要考虑气膜厚度、气膜压力、稀薄气体黏度、轴瓦弹性变形以及Knudsen数等参数间的相互作用。因此,本文作者研究了轴瓦弹性变形和气体有效黏度对微气体滑动轴承静动态特性的影响;利用有限元法求解控制轴瓦位移场的三维弹性方程,推导了包含稀薄气体泊肃叶流流量的广义修正Reynolds方程;通过耦合迭代求解超薄气膜润滑Reynolds方程和三维弹性方程中不断修正黏度项和气膜厚度项,得到不同轴承参数和弹性模量下的微型轴承承载力、摩擦因数以及动态刚度和阻尼系数,并与不考虑气体薄膜有效黏度的刚性轴承结果进行对比。这对于保持高速微旋转机械稳定性具有重要意义。
1 薄膜气体润滑控制方程
对图1所示的微气体滑动轴承,忽略润滑膜中的惯性效应和热效应且假设可压缩气体流动为层流。由于轴颈材料的弹性模量远大于轴瓦材料,轴颈可看作刚性体,不考虑其弹性变形。则考虑稀薄效应和轴瓦弹性变形的修正Reynolds方程可表示为
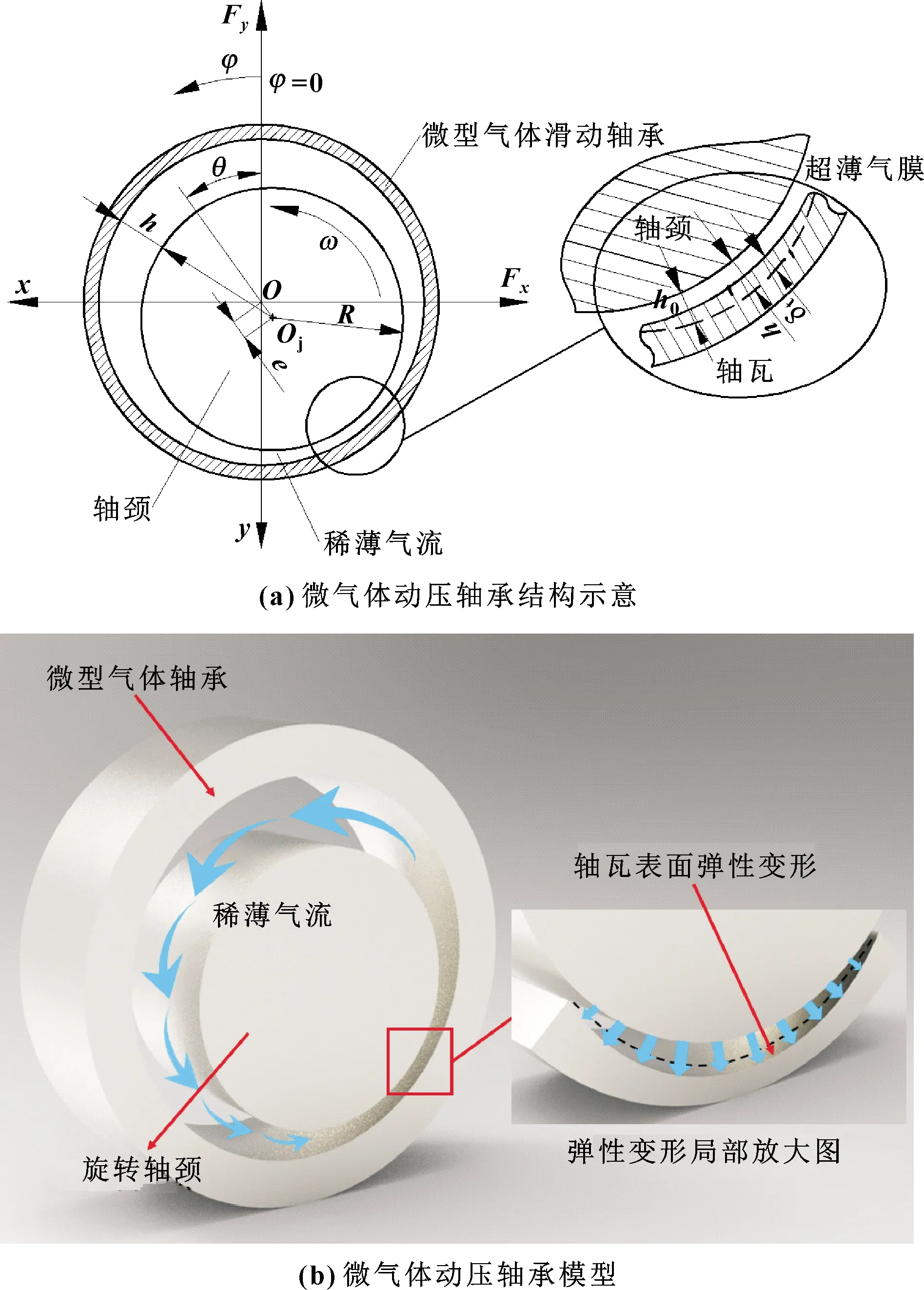
图1 考虑轴瓦弹性变形的微气体滑动轴承结构和三维模型
(1)
式中:量纲一气膜压力P=p/pa;量纲一气膜厚度H=h/c;p为气膜压力;pa为环境气体压力;h为气膜厚度;c为轴承半径间隙;φ=x/R,λ=z/R分别是量纲一周向和轴向坐标,R为轴颈半径;Λeff=6μeffωR2/(pac2)为轴承数,μeff为气体有效动力黏度;ω为轴颈转动角速度;T为量纲一时间;Q为量纲一流量修正系数[24]。
Q=1+0.108 42Kn+9.359 3/Kn-1.174 68
(2)
式中:Knudsen数Kn=λ0/h,λ0为气体分子平均自由程。
学者VEIJOLA和TUROWSKI[4]提出了气体动力黏度也受稀薄效应的影响,即气体有效黏度是Knudsen数的函数,气体有效黏度的计算公式为
(3)
式中:μ为气体润滑剂动力黏度。
为了得到考虑轴瓦弹性变形和气体有效黏度的微滑动轴承静动态性能,通过数学变换PH=S,(PH)2=S2=Π,将方程(1)转化为椭圆型偏微分方程形式求解气膜压力。假设轴颈在弹性微型轴承静平衡位置(ε0,θ0)以扰动频率Ω作周期性小扰动[25],任意时刻的轴颈位置可表示为
(4)
式中:E0和Θ0是扰动偏心率和扰动偏位角定义在复数范围内的幅值;Ω=ν/ω为量纲一扰动频率,ν轴颈扰动频率;i为虚数单位。
在轴颈动态小扰动条件下,假设量纲一气膜压力P和气膜厚度H包含静动态两部分:
(5)
(6)

轴承在水平和竖直方向的气膜合力为
(7)
微气体轴承的偏位角、承载系数和摩擦因数的计算公式为
(8)
将式(5)代入式(1)可得到考虑稀薄效应、轴瓦弹性变形以及气体有效黏度的动态修正Reynolds方程的一般形式:
(9)
为求解式(9)得到微气体轴承的动态刚度和阻尼系数,采用偏导数法定义:
(10)
式(6)和(9)分别对E0和Θ0求偏导,可得到关于PE、HE、Pθ和Hθ的偏微分方程,求得PE和Pθ后,按式(11)计算轴颈小扰动时微气体滑动轴承的动态刚度和阻尼系数。
(11)
将式(9)中的动态系数进行转换,得到相应笛卡尔坐标系下的动态刚度和阻尼系数为
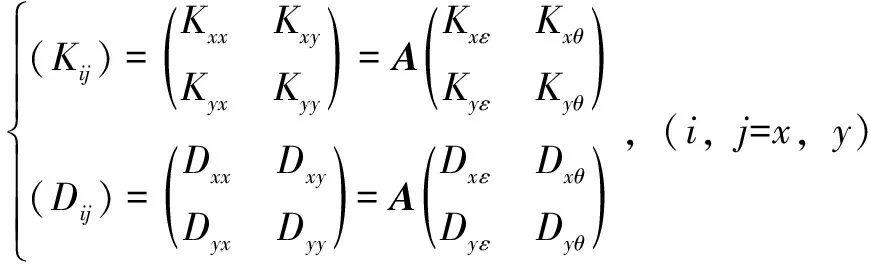

(12)
通过MATLAB软件中偏微分方程工具箱和有限元法编写相关程序,采用松弛迭代法提高计算的精度和效率,收敛精度均为 0.000 1,微型气体轴承弹流润滑的计算流程如图2所示。

图2 微型气体轴承弹流润滑计算流程
2 轴瓦弹性变形和气膜厚度变化
微型滑动轴承在气膜压力作用下导致轴瓦表面发生弹性变形,而表面弹性变形直接改变气膜厚度反过来也会影响气膜压力分布。由于轴瓦表面弹性变形量很小,因此可认为变形和载荷呈线性关系,利用有限元法建立轴瓦柔度矩阵求解轴瓦表面弹性变形。
如图3所示,将微气体滑动轴承沿圆周方向展开,由于轴瓦厚度远小于轴瓦展开后长度,轴瓦模型近似为规则的长方体,采用八节点六面体线性单元将模型离散;根据最小位能原理得到各单元体的节点位移和节点载荷间的关系,再将各单元的刚度矩阵进行组装,建立轴瓦模型结构的整体刚度矩阵为

图3 微气体轴承的有限元模型
K=∭VBTDBdxdydz
(13)
式中:
B=[B1B2B3……B8],
(i=1,2,3,...,8)
(14)
(15)
其中N为形函数。
对整体刚度矩阵求逆矩阵得到微型轴承的柔度矩阵C来确定气膜压力引起的轴瓦上表面各节点径向变形。
δt=∑C·P=∑K-1·P
(16)
式中:δt为气膜压力矩阵P下微型轴承内表面所有节点的径向位移矩阵。
通过计算微型轴承表面的弹性变形对气膜厚度进行修正
H=H0+δt=1+εcos(φ-θ)+δt
(17)
在求解修正Reynolds方程得到气膜压力的每次循环迭代中计入有限元法求解轴瓦弹性变形和气体有效黏度的影响,最终同时达到收敛,得到考虑气体有效黏度的弹性微气体滑动轴承的静动态性能。
3 结果及讨论
文中对考虑和不考虑气体有效黏度的刚性和弹性微气体滑动轴承计算结果进行了分析和讨论。微型轴承的几何参数:c=1 μm,R=1 mm,轴承宽度B=200 μm,pa=1.033×105Pa,长径比B/D=0.1。
为验证当前模型的准确性,如图4所示,将文中计算结果与文献[26]给出的轴承中间截面量纲一气膜压力分布进行对比,可以看出2种方法得到的仿真结果非常接近,误差小于3%。

图4 文中数值结果与文献[26]量纲一气膜压力分布对比(R=2.0 mm,B=0.4 mm,pa=1.033×105 Pa,Λ=2.4)
图5所示为分别计入轴瓦弹性变形和同时计入气体有效黏度条件下微型轴承量纲一承载力CL随轴承数Λ的变化规律。可以看出,气体稀薄效应显著降低轴承承载力,微气体轴承的承载力随轴承数的增加近似线性增加,这与润滑表面的高轴颈转速和气体的可压缩性有关。而CL随轴瓦弹性模量降低而增加,这是因为气体弹流润滑状态在一定程度上削弱了气体稀薄效应的影响。不考虑气体有效黏度的弹性微型轴承量纲一承载力大于考虑气体有效黏度的情况。轴瓦弹性变形和轴承数越大CL增加越明显。

图5 轴承数、气体有效黏度和轴瓦弹性模量对承载力的影响(ε=0.7,υ=0.3)
对于不同柔性的微型轴承,其轴颈表面摩擦因数随轴承数的变化曲线如图6所示。由于微气体滑动轴承的摩擦来自稀薄气流的黏性剪切力,轴承数越高,即轴颈转速越高,黏性剪切力则越大,因此轴承数对摩擦因数的影响就越明显。随着轴瓦弹性模量E降低,微型轴承柔性增加,轴颈表面摩擦因数增大。这是由于气膜厚度随弹性模量的减小而增大,更多的气流进入超薄润滑间隙导致轴颈表面摩擦因数增加。此外,考虑气体润滑剂的有效黏度时,微型轴承摩擦因数低于气体黏度不变时的结果。
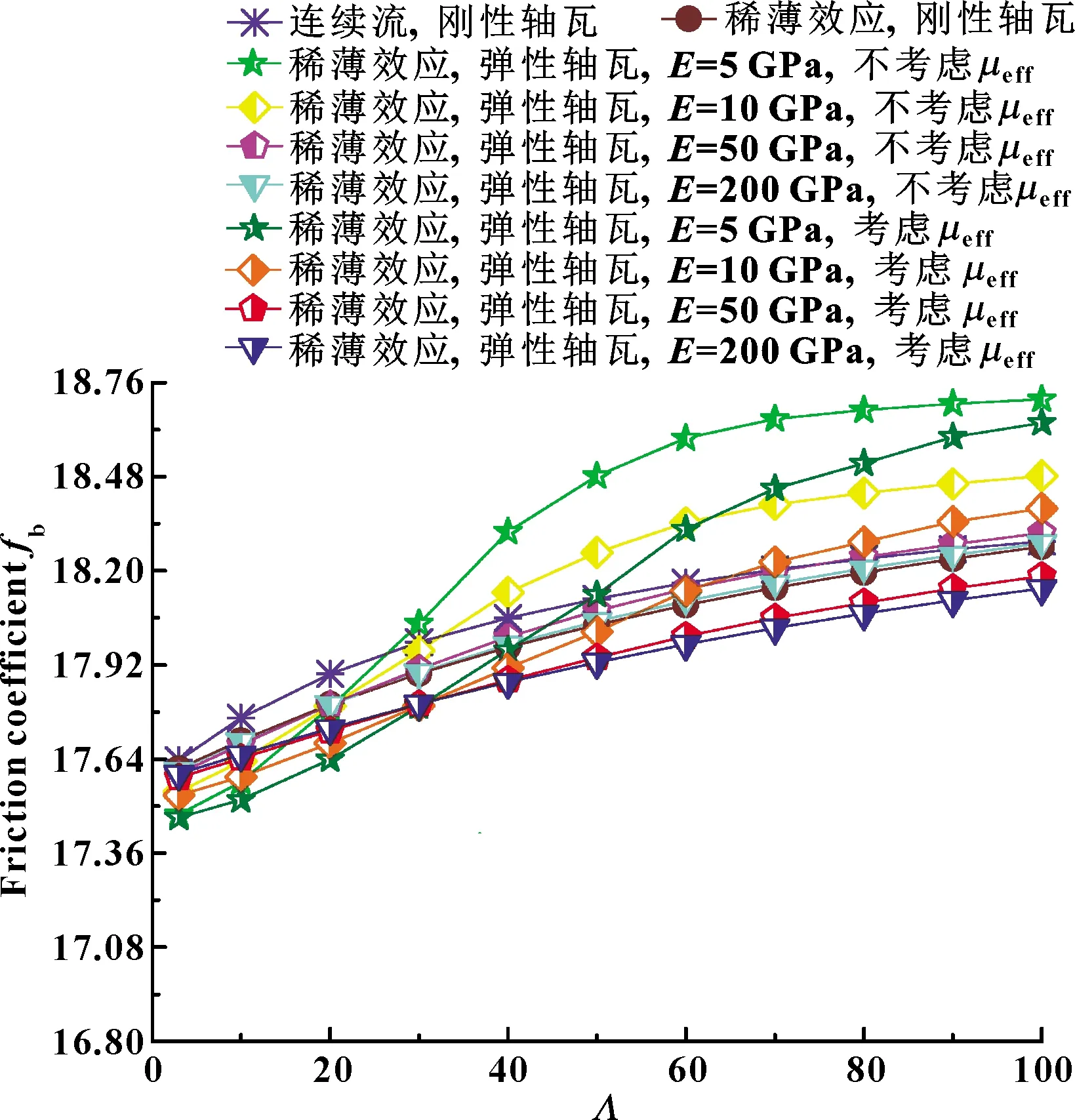
图6 轴承数、气体有效黏度和轴瓦弹性模量对摩擦因数的影响(ε=0.7,υ=0.3)
图7描述了计入不同轴瓦柔性和气体有效黏度的量纲一承载力CL随偏心率ε的变化情况。结果表明,随偏心率的增大,微型轴承的承载能力越来越强。当偏心率ε<0.7时,随轴瓦弹性模量从5 GPa增加到200 GPa,量纲一承载力CL逐渐增大。而在ε较高时,CL随E的增大呈现出相反的变化趋势,这是因为轴瓦弹性变形增加了气膜承载区域从而弹性微型轴承的承载能力增强。考虑稀薄气体有效黏度的影响,随着ε的增加进一步降低了弹性微型轴承的承载力CL。

图7 偏心率、气体有效黏度和轴瓦弹性模量对承载力的影响(Λ=30,υ=0.3)
图8和9分别示出了在不同轴瓦弹性模量E和量纲一扰动频率Ω条件下,考虑和不考虑稀薄气体有效黏度的微型轴承动态刚度和阻尼系数计算结果。可以看出,刚性和弹性2种微型轴承情况下,随着Ω的增加,正交刚度系数Kxx和Kyy均增大,交叉刚度系数Kyx减小而Kxy先增大后减小。由于润滑薄膜主要在垂直方向支承转子重力,因此Kyy略大于Kxx。与刚性微型轴承相比,弹性微型轴承中轴瓦弹性模量的降低使动态刚度系数有所增加且随着轴承柔性上升其刚度系数增加幅度更显著。这是由于轴瓦弹性变形带来气膜厚度增加导致流过轴承间隙内的气流增加。微气体滑动轴承的动态阻尼系数除了交叉阻尼Dyx均随扰动频率的增加而减小。当弹性模量减小,弹性微型轴承的直接阻尼系数小于刚性微型轴承。与恒定黏度气体润滑相比,当扰动频率Ω>2时,气体有效黏度效应降低了微型轴承的直接刚度,同时增加了其直接阻尼系数,刚性和弹性微型轴承的交叉耦合阻尼系数的绝对值均随Ω的增大而趋于0。
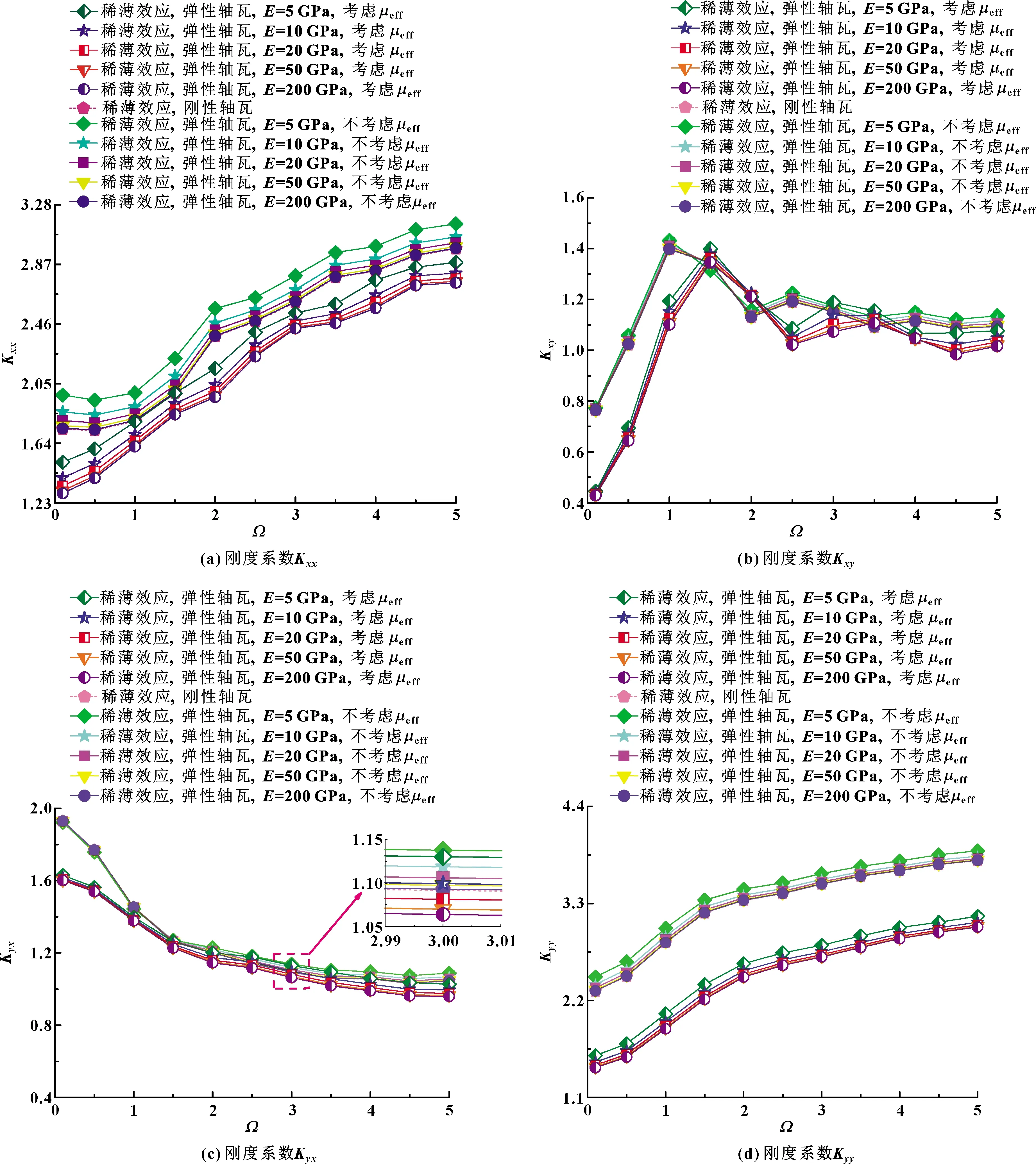
图8 扰动频率、气体有效黏度和轴瓦弹性模量对刚度系数的影响(ε=0.7,Λ=80,υ=0.3)
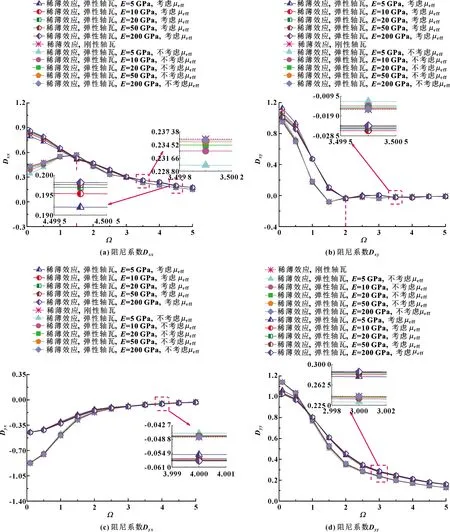
图9 扰动频率、气体有效黏度和轴瓦弹性模量对阻尼系数的影响(ε=0.7,Λ=80,υ=0.3)
图10和11分别给出了当扰动频率Ω=3.5和偏心率ε=0.7时,计入不同轴瓦弹性模量和气体有效黏度效应的微气体轴承动态刚度和阻尼系数随轴承数Λ的变化曲线。可以看出,所有的动态刚度系数均随着轴承数的增加而增加,而动态阻尼系数除了交叉阻尼Dyx均呈现出先增加后减小的趋势。与刚性微气体轴承相比,当Λ>30时,刚度系数随轴瓦弹性模量减小而显著增大,相反直接阻尼系数变小。这是因为较高的轴承数,即高轴颈转速增强了微气体滑动轴承中的动压效应,有效减少了超薄轴承间隙中的能量耗散。另外,气体润滑剂的有效黏度效应显著降低了微型轴承的直接刚度系数,并增加了微型轴承的直接阻尼系数。这表明如果应用恒定气体黏度计算超薄气膜润滑特性,会导致计算的动态阻尼系数偏小。
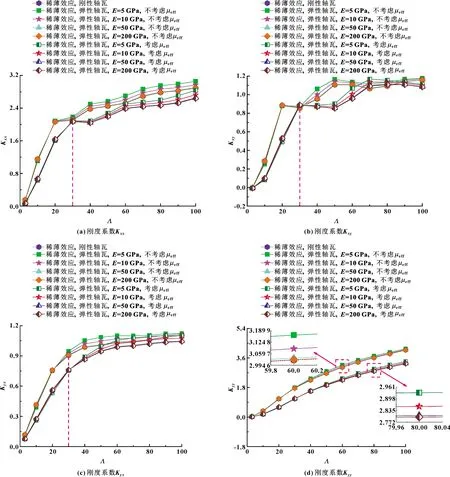
图10 轴承数、气体有效黏度和轴瓦弹性模量对刚度系数的影响(Ω=3.5,ε=0.7,υ=0.3)

图11 轴承数、气体有效黏度和轴瓦弹性模量对阻尼系数的影响(Ω=3.5,ε=0.7,υ=0.3)
4 结论
基于VEIJOLA提出的稀薄气体有效黏度模型,利用偏导数法、松弛迭代法和有限元法对修正的Reynolds方程和轴瓦弹性方程进行了耦合数值求解。结果表明稀薄效应、轴瓦弹性变形以及气体有效黏度对微气体滑动轴承润滑特性有显著影响。一些重要规律总结如下:
(1)气体稀薄效应显著降低了微型轴承的承载能力。量纲一承载力和摩擦因数随轴承数的增加而增加。由于气体弹流润滑状态一定程度降低了稀薄效应的影响,轴瓦柔性的增加可提高轴承承载力和摩擦因数。相比恒定气体黏度润滑的刚性微型轴承,考虑气体有效黏度的弹性微型轴承承载力和摩擦因数较小。
(2)微气体轴承的量纲一承载力随偏心率增加越来越高。当偏心率较小时,随着轴瓦弹性模量的增加,轴承承载力增大。而在大偏心率情况下,量纲一承载力随微型轴承柔性增加略有增加。
(3)正交刚度系数Kxx和Kyy随扰动频率的增加而增加,而动态阻尼系数除交叉阻尼系数Dyx均随扰动频率的增加而减小。微气体滑动轴承的动态刚度系数均随着轴承数的增加而增加,而相应的动态阻尼系数除了交叉阻尼Dyx均呈现出先增加后减小的趋势。相比刚性微气体轴承,轴瓦柔性的提高显著增加了动态刚度系数且降低了微型轴承的直接阻尼系数。稀薄气体的有效黏度效应降低了微型轴承的直接刚度,同时增加了其直接阻尼系数。
