多成像模式下舰船目标SAR成像仿真*

张寅，范君杰，闫钧华，章琪琪，夏翀翔

（南京航空航天大学a.空间光电探测与感知工业和信息化部重点实验室；b.航天学院，江苏 南京 211106）

0 引言

合成孔 径雷达（synthetic aperture radar，SAR）是一种通过二维匹配滤波获取高分辨率图像的主动探测技术。SAR利用天线与目标相对运动产生的多普勒信息，将小孔径天线的运动等效成较大的合成孔径，提高方位向分辨率［1-2］，利用脉冲压缩技术提高距离向分辨率［3］。与传统光学传感器相比，SAR具有抗干扰能力强、全天时、全天候、一定的云雾穿透性等优点，是一种应用前景广阔的广域远距离感知手段。

SAR广泛应用于军事侦察领域，成像特性对视角、平台运动等观测条件较为敏感。在目标检测与识别研究中，为提高识别率需要大量不同成像条件下的SAR图像数据进行学习和训练。实测SAR图像难以获得，无论从数量还是条件覆盖性上均无法满足要求。因此，通过建立波束传输物理模型进行数字仿真成为数据获取的重要途径［4］。另一方面，通过研究SAR图像仿真技术，有助于理解不同工作模式、工作参数条件下SAR电磁波与目标的作用机理，提升目标与背景特性认知水平，促进SAR图像目标检测与识别技术发展［3］。

本文针对条带模式、聚束模式、扫描模式下舰船目标SAR成像仿真方法开展研究。首先，根据SAR典型工作模式成像机理，建立电磁信号发射与回波传输模型；其次，基于面元法将舰船目标三维模型划分为多个小三角形面元，利用弹跳射线（shooting and bouncing ray，SBR）法计算目标的散射回波强度；然后，利用距离多普勒（range-Doppler，RD）回波处理算法得到仿真图像。最后，以典型舰船目标为例，进行SAR成像仿真实验与验证。

1 多成像模式SAR成像仿真原理

1.1 典型SAR成像模式

SAR有多种成像模式，其中最为常见的3种成像模式分别为条带模式、聚束模式和扫描模式［5-6］，如图1所示。条带模式（图1a））下的SAR在成像时，其天线始终指向同一方向，方位向分辨率在一定范围内随天线孔径的减小而提高［7］。聚束模式（图1b））通过控制天线转动使其波束指向某一固定区域，增加了合成孔径长度，以牺牲成像范围的方式来提高方位向分辨率［8］。扫描模式（图1c））在平台运动的过程中，天线波束沿距离向周期性扫描多个子带，利用先后扫描测绘带的重叠部分，对各子带所成图像进行拼接，以牺牲方位向分辨率的方式获得测绘区域远大于条带模式的图像。

1.2 典型成像模式发射信号模型

如图2所示，P为成像区域内的一个目标，R(t)为目标的斜距。SAR在运动过程中，以一定的周期向成像区域发射线性调频脉冲信号，经目标散射后形成回波信号，再被载机接收［9］。

图2 SAR成像几何关系图Fig.2 SAR imaging geometry

用慢时间ts描述线性调频脉冲信号的发射时间，用快时间t描述雷达电波传播时间，则SAR的发射信号是关于慢时间ts和快时间t的二维函数s(ts，t)。条带模式和聚束模式下，SAR对成像区域进行连续成像，其发射信号为［10-11］

式中：θ(t)为线性调频脉冲信号的相位；Kr为线性调频率；f0为信号初始频率；函数rect(⋅)为矩形窗函数。

在扫描模式下，SAR依次对各个子带进行扫描。SAR扫描各子带的时序如图3所示，Tp为扫描周期；Tb为一个扫描周期内天线波束在一个子带的驻留时间。

图3 SAR扫描模式时序关系图Fig.3 Time sequence of SAR scanning mode

因此，扫描模式SAR对某一条子带的发射信号是不连续的，其表达式为

1.3 典型成像模式回波信号模型

由于SAR回波系统是线性的，因此目标的回波等于目标各面元散射中心回波之和［12］。

条带模式和聚束模式下，划分为M个面元的舰船目标的回波信号可以表示为

式中：σi为第i个可见面元的雷达散射截面（radar cross section，RCS）；w为雷达的双向天线方向图加权；τi为第i个面元的回波的延时；Ri(ts)为第i个面元与雷达的瞬时斜距；c为光速。

扫描模式下，某子带内划分为M个面元的舰船目标的回波信号为

电磁波会在舰船目标表面产生多次散射，故使用弹跳射线（shooting and bouncing ray，SBR）法以快速计算目标各面元的RCS［13-15］。弹跳射线法结合物理光学法和几何光学法，产生大量由波源射向目标的射线管来模拟入射电磁波，利用几何光学法计算电磁波在目标面元间的散射；而当电磁波发生最后一次散射离开目标时，利用物理光学法计算其远场散射功率。

1.4 SAR成像算法

SAR在沿方位向运动过程中持续进行成像，目标各面元的回波信号将在慢时间ts和快时间t的二维时间域上发生混叠。本文采用经典的RD成像算法［16］进行计算，将各面元回波分散在二维时间域上的强度集中于一点，从而解除回波的混叠，得到方位-距离二维图像。图4为RD成像算法的流程图。扫描模式下单个子带的SAR成像算法与条带模式和聚束模式相同，但需要对得到的各个子带图像进行拼接才能得到完整的扫描图像。

图4 RD成像算法流程图Fig.4 Flow chart of RD imaging algorithm

2 仿真结果及分析

本文仿真所使用的舰船目标为阿利·伯克级驱逐舰，尺寸为158.3 m×20.3 m，图5为该驱逐舰的三维模型及其面元划分，驱逐舰表面共划分为7 184个三角形面元。由于阿利·伯克级船体表面大部分采用钢合金、铝合金、钛合金等良导体，在L～X波段下的趋肤深度为1μm左右，且其表面的灰漆对于电磁波的散射影响较小，故将所有的面元视作厚度为0的理想导体三角面。

图5 驱逐舰三维模型及其面元划分Fig.5 3D model and surface segmentation of a destroyer

2.1 典型成像模式图像仿真

参考文献［8］给出的机载SAR典型参数，如表1所示。分别得到条带模式、聚束模式、扫描模式下阿利·伯克级驱逐舰的SAR回波数据和仿真图像，如图6所示。

图6a）为舰船目标在条带模式下的仿真图像，由于条带模式下SAR的方位向分辨率为真实天线孔径的0.5倍，因此在表1的参数下，条带模式SAR的方位向分辨率只有2 m。图6c）为舰船目标在聚束模式下的仿真图像，聚束模式SAR的方位向分辨率和SAR平台在聚束时间内运动的距离即合成孔径长度有关，而与真实天线孔径无关，因此在相同的天线孔径下，聚束模式能实现更高分辨率的成像。图6e）为舰船目标在三子带扫描模式下某一子带的仿真图像，由于仿真时对3个子带进行扫描，因此扫描模式下SAR的方位向分辨率是相同成像参数下条带模式的3倍，即6 m。虽然扫描模式成像的方位向分辨率较大，但将扫描模式的3个子带图像拼接后，其距离向成像范围是相同参数下条带模式的3倍。因此，若要对大范围区域成像而对分辨率无过高要求，可考虑扫描模式。

表1 SAR成像仿真参数Table1 Parameters of SAR imaging simulation

图6b），d），f）分别为上述3张仿真图像对应的原始回波数据。可见，条带模式和聚束模式下的回波数据是连续的，而扫描模式下的回波数据是不连续的，这是由于扫描模式下SAR天线在某子带的非驻留时间内既不向该子带发射信号也不接收该子带的回波信号。

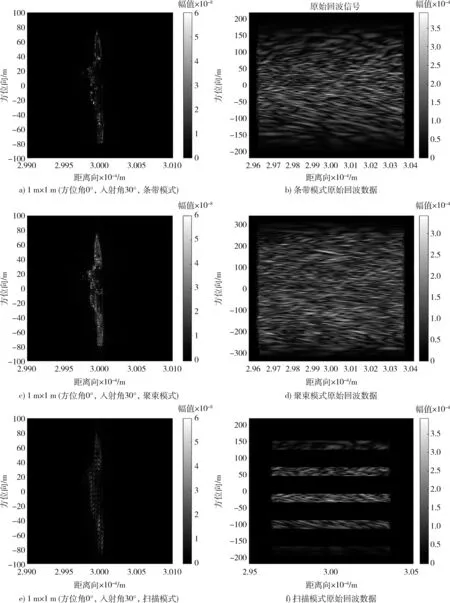
图6 多成像模式仿真图像及其回波数据Fig.6 Simulated images and echo data of multi-mode SAR

2.2 多成像角度图像仿真

图7a），b）和c）分别为表1成像参数下，方位角为0°，45°，90°时的聚束模式仿真图像。可以看出，不同方位角下的舰船目标的SAR图像具有显著差异。在进行目标检测与识别时，针对光学图像的旋转等数据增强方式对于SAR图像效果较差，而仿真SAR图像能较真实地反映不同成像角度下SAR图像的特征，能有效补充SAR图像数据集。

与光学图像不同，SAR图像的2个坐标分别代表相对于雷达方位和斜距，因此，SAR图像具有阴影、叠掩、透视收缩等特征。图7d）为入射角为60°时的聚束模式仿真图像，相较于图7a），图7d）由于入射角更大，目标处于阴影区的部分更多了，阴影效果更加明显；同时，目标在斜距上的叠掩效果更强，在图像上表现为叠掩区域亮度更大。

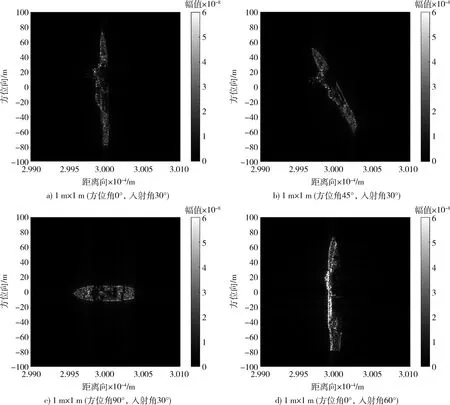
图7 多成像角度仿真图像Fig.7 Simulated SAR images of multiple angles

2.3 多次散射效应对仿真图像的影响

由于舰船目标具有较多二面角结构，电磁波在舰船表面将发生多次散射，所以单纯利用物理光学法等基于一次散射的电磁计算方法会引入较大误差。图8 a），b）分别为表1成像参数下，使用物理光学法和弹跳射线法计算舰船目标回波得到的SAR聚束模式仿真图像。由于弹跳射线法考虑了电磁波的多次散射效应，因此图8 b）中舰船目标的桅杆、炮台、上层建筑与甲板连接部分等二面角结构处亮度明显强于图8 a）。将仿真图像应用于图像检测与识别时，考虑多次散射的仿真图像更能真实地反映目标图像的特性，因此本文使用SBR算法计算目标的回波是合理的。

图8 考虑/未考虑多次散射效应的仿真图像Fig.8 Simulated images with/without considering multiple scattering effects

2.4 仿真图像和实测图像的对比

为说明本文提出仿真方法的有效性和准确性，进行SAR仿真图像和实测图像的对比。由于缺少公开的舰船目标实测数据，本文使用哨兵一号A星（Sentinel-1A）在条带模式下拍摄的SAR图像作为实测图像。图9a）为一型号未知的舰船图像，截取自表2成像参数下哨兵一号A星于2014-10-30 T 05：16（UTC时间）拍摄的荷兰阿姆斯特丹附近海域（E5°，N52°）的图像；图9b）为在该成像参数下仿真得到的阿利·伯克级驱逐舰的图像。

图9 SAR实测图像和仿真图像Fig.9 Comparison of measured and simulated SAR images

表2 哨兵一号A星部分成像仿真参数Table 2 Some parameters of Sentinel-1A satellite for SAR imaging simulation

目前，国内外常用于评价SAR图像仿真性能的指标主要有均值、方差、峰值旁瓣比等，但上述指标难以同时满足评价的直观性和高效性。因此，本文采用改进的Hausdorff距离测度和归一化交叉相关系数（normalization cross correlation，NCC）来评价仿真图像。

Hausdorff距离测度定义为

归一化交叉相关系数定义为

式中：I1和I2分别为仿真图像和实测图像的灰度矩阵和分别为I1和I2的均值。归一化交叉相关系数代表了2幅图像的匹配相关性，其越接近1，说明2幅图像匹配性越好。

图9实测图像与仿真图像的Hausdorff距离测度为0.075 1，接近于0，说明实测和仿真得到的舰船目标图像形态非常相似，且舰船在图像上的成像位置一致。实测图像与仿真图像的归一化交叉相关系数为0.69，接近于1，说明仿真图像和实测图像中散射中心分布和亮度比较接近。由于仿真图像和实测图像中的2个舰船目标不是同一型号，所以散射中心分布和亮度不可能完全一致。但是2个目标同为舰船，散射中心分布和亮度也具有一定相似性，因此实测图像与仿真图像的归一化交叉相关系数达到了0.69，也能验证本文仿真方法的可靠性。

3 结束语

本文建立了条带模式、聚束模式、扫描模式等典型工作模式下SAR电磁信号发射与回波传输模型，提出一种基于面元法和弹跳射线算法的SAR成像仿真方法。通过仿真实验，验证了方法的有效性。该方法可应用于目标检测与识别领域，为舰船目标电磁散射特性研究提供支持，也可作为SAR图像数据集补充的有效手段。