双电机同步消隙伺服系统的鲁棒滑模控制策略*
2022-05-19李方俊王生捷
李方俊,王生捷
(北京机械设备研究所,北京 100854)
0 引言
针对某大惯量交流伺服系统,如何克服末端齿轮传动结构齿隙对系统控制性能的影响具有十分重要的意义。在单电机驱动控制方案中,国内外众多学者提出了许多消除齿隙影响的算法,如根据齿隙的数学模型,在反步法设计过程中对齿隙进行补偿[1-4];利用状态观测器对齿隙大小进行估计[5-6]。但以上方法对系统模型建立精度要求较高,且算法实现复杂,传动结构存在较大的变形与应力,故在大惯量齿轮传动系统中常采用双电机同步消隙驱动方案[7-9]。
常见的双电机同步消隙伺服系统由电流环、速度环以及位置环构成,采用变偏置力矩曲线施加置电流环上对齿隙进行补偿。此种方法不依赖于齿隙的数学模型,控制算法实现简单,延长了机械结构的使用寿命[10]。同时,采用交叉耦合方式来减小两侧电机速度偏差引起的结构冲击[11-13]。但此种控制方法仍存在不足之处,如系统响应速度较慢且对内部结构参数变化以及外部扰动鲁棒能力较弱,在运行过程中产生的冲击力将打破系统的静态平衡,甚至引起结构的抖动。
本文提出了一种以反步控制理论为基础,仅由位置环和电流环构成的新型双电机同步消隙伺服系统控制方案。在控制器设计过程中引入了一种积分非奇异终端滑模面,削弱了滑模控制常见的抖动问题,使得系统在有限时间内达到平衡状态;系统的参考位置指令采用指令滤波的方式,避免了在控制器设计中求导过程导致的控制量过大的问题。为了克服外在扰动的影响,系统引入了扩张状态观测器对扰动力矩进行补偿。在Matlab/Simulink与Adams中的联合仿真实验结果,证明了本文所设计方案能有效提高双电机同步消隙伺服系统的响应能力及鲁棒性能。
1 双电机同步消隙系统数学模型
如图1所示为双电机驱动系统的示意图,从图中可看出,两侧电机输出力矩经减速器作用后传递至系统末端的齿轮传动机构,从而带动负载运行。
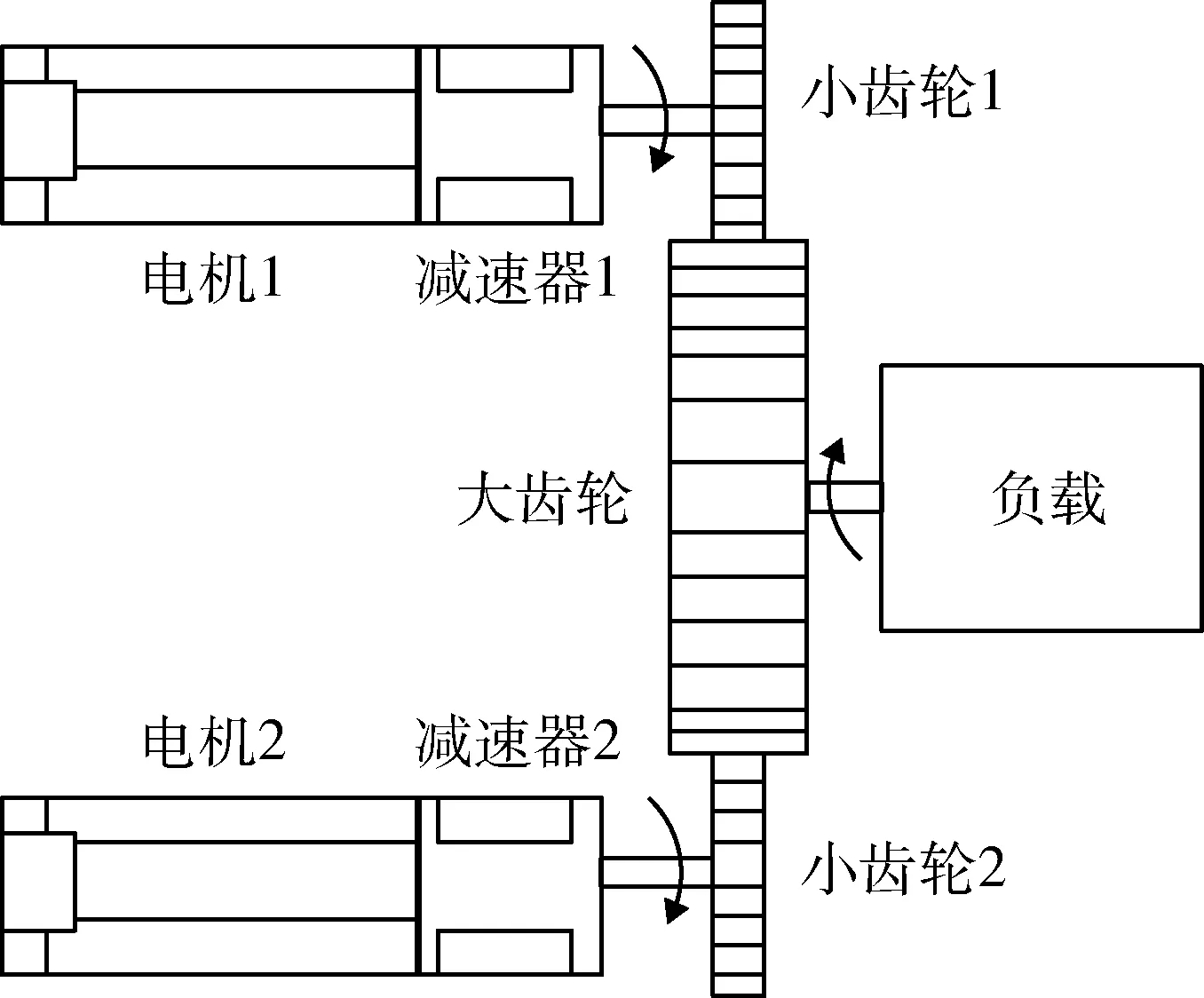
图1 双电机驱动系统Fig.1 Dual-motor driving system
由于永磁同步电机体积小、功率密度大的特点,在交流传动系统中得到了广泛的应用,其数学模型可以表示为
式中:Ld,Lq为d,q轴电感;id,iq为d,q轴电流;Ud,Uq为d,q轴电压;R为定子电阻;λf为转子磁链;ωe为电角速度;np为电机极对数;Te为电磁力矩。
经减速器作用后,系统的动力学方程可表示为
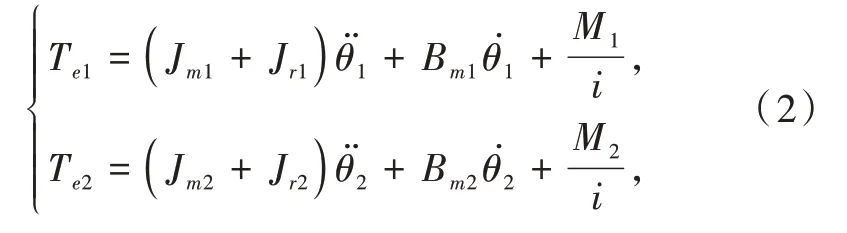
式中:Jm1,Jm2为电机转动惯量;Jr1,Jr2为减速器转动惯量;θ1,θ2为电机转动机械角度;Bm1,Bm2为动摩擦因数;M1,M2为减速器输出力矩;i为减速器传动比。
减速器输出至末端小齿轮结构的动力学方程为

式中:Jg1,Jg2为小齿轮转动惯量;θg1,θg2为小齿轮转动角度;Bg1,Bg2为动摩擦因数;Mg1,Mg2为大小齿轮间的传递力矩。
齿轮传动结构间的动力学方程为

式中:Jm为大齿轮与负载的转动惯量;θG为大齿轮的转动角度;Bm为动摩擦因数;Mm为大齿轮与负载的驱动力矩;TL为外部扰动力矩;iG为大小齿轮的传动比。
由于齿隙的影响,大小齿轮间的传递力矩变化并不连续,根据常见的齿隙死区模型,其数学模型可表示为

式中:Δ为齿隙的间隙大小;K为齿轮间的接触力刚度系数;C为接触摩擦系数。为了克服齿隙的影响,在双电机驱动伺服系统中常采用预加变偏置力矩的方式来补偿结构中的传动间隙,原理图如图2所示。
如图2所示,根据参考电流指令输入值的大小,可将偏置电流曲线分为3部分:
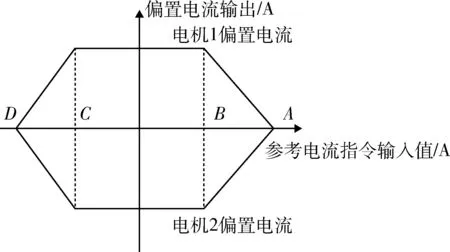
图2 变偏置电流原理图Fig.2 Var iable bias cur r ent schematic diagr am
(1)在BC段内,施加于两侧电机的偏置电流处于最大值且方向相反,此时双电机处于互相出力阻碍运动状态。
(2)在AB与DC段内,随着负载的逐渐增加,参考电流指令绝对值也逐渐变大,这一过程中为了提高电能的利用率,将使偏置电流曲线以固定速率恒定衰减。
(3)当负载在原有基础上进一步变大,参考电流指令绝对值已超出AB段与DC段的范围,两侧电机偏置电流大小衰减为0。
为了保持双电机驱动系统中两侧电机的转速平衡,减小两侧电机转速差异引起的结构冲击,在双电机同步消隙伺服系统中常采用交叉耦合均速负反馈方式设计系统的转速闭环,系统的传动部分控制框图如图3所示。
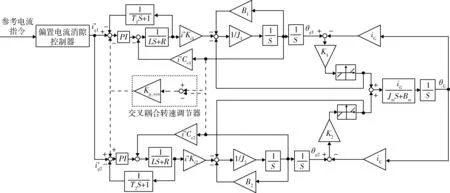
图3 系统传动部分控制框图Fig.3 Control block diagram of the system transmission part

式中:T1,2为电流滤波系数;Kt1,t2为 电 机 力 矩 系 数;Ce1,e2为反电势系数;Kp_syn为转速同步调节器比例系数。
2 新型双电机驱动算法设计
2.1 反步积分非奇异终端滑模(BINTSM)控制器设计
为了简化传统双电机同步消隙伺服系统的控制结构,提高系统的响应能力及鲁棒能力,本文基于反步控制理论设计了系统的新型控制算法,具体过程如下:
依据式(4),可将大齿轮及负载动力学方程改写为

式中:ωG为大齿轮转动角速度;u为两侧电机驱动大齿轮及负载运行的驱动力矩。
令x1=θG,x2=ωG,ϑ=Bm Jm,Λ=TL/Jm,yr为位置指令参考值,依据反步法构造新的状态变量z1,z2为

式中:α1为反步法中的虚拟控制变量,现构造第1步Lyapunov函数为

则
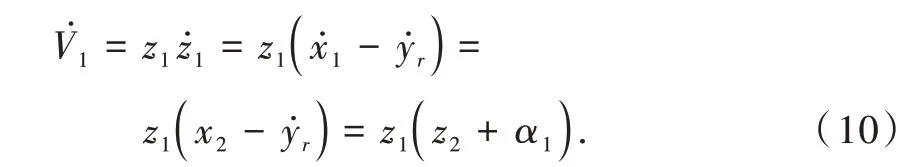
令α1=-c1z1(c1为正比例系数),代入式(10)可得
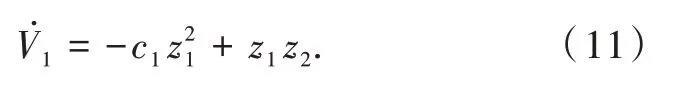
由式(11)可知,当z1,z2趋近于0时,能保证V̇1≤0,因此V1正定,V̇1负定,能保证第1步Lyapunov函数的稳定。
下一步为了提高系统的响应能力及面对结构参数变化的鲁棒能力,在此步设计中引入了积分非奇异终端滑模面。相较于其他滑模面,积分非奇异终端滑模面具有控制量抖动小,收敛速度快的优点[14-15],因此可设计反步法的第2步Lyapunov函数为


这里采用指数趋近率Ṡ=-Dsgn(S)-Ks S,D>0,Ks>0,对控制器输出u进行计算可得

考虑到齿隙已被前文所述变偏置力矩方法所补偿,可得

则最终反步积分非奇异终端滑模(backstepping integral nonsingular terminal sliding mode,BINTSM)控制器的输出电流参考值为

2.2 稳定性证明
将式(14)代入(13)中可得

现对的稳定性进行讨论:
通过选取D值可使D≥|Λ|成立,则D|S|+ΛS≥0成立;由于β,p,q,Ks均为正数,故对的正负进行分析:

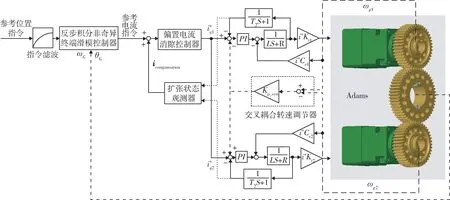
由于p,q均为奇数且q 可知反步法所设计第2步Lyapunov函数V2稳定性成立,故积分非奇异终端滑模面将在有限时间内收敛至0,此时状态变量z2也将保持为0状态,则第1步Lyapunov函数V̇1≤0成立,状态变量z1将在有限时间内趋于0状态,系统实际位置到达指令位置。根据式(12)中的控制器输出表达式,符号函数sgn()的不连续性将使控制量存在高频抖动部分,可能会激发系统的高频特性从而影响系统的稳定,故本文在算法中针对符号函数做如下处理,选择饱和函数sat()来取代符号函数: 这样将使控制量连续变化,削弱其高频抖动部分;针对在控制率中对参考位置指令求一阶导数甚至二阶导数的计算,为了避免如阶跃信号求导后引起控制量过大的问题,本文采用指令滤波的方式对位置参考信号进行了平滑处理。 由于双电机同步消隙伺服系统中存在着各种扰动力矩,如摩擦力矩、冲击干扰力矩等,本文为了有效抑制这些扰动因素采用了扩张状态观测器(ex‑tended state observer,ESO)对 这 些 扰 动 进 行 补偿[16-17]。扩张状态观测器能将系统的各种扰动总和进行处理,无需依赖系统的精确模型,具有很强的实用性。根据式(7)且考虑到系统结构参数的变化,可将大齿轮及负载动力学方程重写为 令x1=ωG,则式(21)可重写为 式中:h为总扰动的变化率;现可设计线性扩张状态观测器(liner ESO,LESO)为 则根据式(22)与式(23)可得观测误差矩阵为 式中:λ为误差矩阵特征值;I2为二阶单位矩阵;ωf为设计观测器的带宽。 解式(25)可得 为了避免噪声的影响,观测器带宽ωf不宜设计过大,且考虑到双电机同步消隙伺服系统中的齿隙已被变偏置力矩所补偿,则观测器输入可表示为 观测器输出反馈至系统电流环的补偿值为 根据式(5)中所示的齿隙数学模型,可知在运行过程中齿隙间传递力矩大小是会随着齿隙变化而变化。如何更精确地对齿隙模型进行仿真且考虑到齿隙变化的动态过程,本文提出了基于Matlab/Simulink与Adams的联合仿真方式,即在Simulink中运行控制算法与逻辑,在Adams中进行动力学的仿真。在三维建模软件中创建好模型后导入至Ad‑ams,在Adams中对齿轮结构添加接触力约束,以物体嵌入深度与速度作为接触力大小计算的依据,故在Adams中对齿轮传动机构的仿真更符合实际工况。建立好的新型双电机同步消隙伺服系统控制框图如图4所示。 图4 新型双电机同步消隙伺服系统控制框图Fig.4 Control block diagram of the new dual-motor synchronous anti-backlash servo system 仿真所用表贴式永磁同步电机、齿轮传动结构参数如表1所示。 设定仿真对比实验为PID型常规双电机同步消隙伺服系统、PID+ESO型扰动补偿双电机同步消隙伺服系统和BINTSM+ESO型新型双电机同步消隙伺服系统。将分别对各方案的系统响应能力及抗扰动能力进行仿真实验分析,对于各方案中共有的偏置电流消隙控制器和交叉耦合转速调节器,其参数设置如下:偏置电流幅值为5 A,参考电流为0;交叉耦合转速调节器参数Kp_syn为2。电指令值大小为7.5 A时开始衰减,直至10 A时变流环滤波系数T1,2为0.01,电流参考指令限幅值为30 A,各方案控制器参数设计规则如表2所示。 表2 控制器设计参数Table 2 Controller design parameters 现给定系统空载条件下0.4 s到达1 rad的阶跃位置指令信号,得到各方案下系统状态响应曲线如图5,6所示。 图5 空载阶跃位置指令响应曲线Fig.5 Response of the step position command with no load 从以上的阶跃位置信号响应图可以看出,在空载条件下,以反步积分非奇异终端滑模(BINTSM)控制器为核心的新型双电机同步消隙伺服系统能得到更快的响应速度,比常规PID型双电机同步消隙伺服系统提高约2 s的到位时间;从电流信号的变化也可看出,BINTSM控制方法能得到更快的力矩响应,到达稳态时2种方式下两侧电机电流值大小均为5 A,符合消隙控制器的设计要求。 图6 空载阶跃位置指令电流响应曲线Fig.6 Current response of the step position command with no load 现再给定空载条件下周期4 s幅值为1 rad的正弦位置指令信号,得到的系统状态响应如图7,8所示。 从图7可以看出,BINTSM控制方法具有更快的跟踪速率,且位置曲线变化平滑,不受齿隙的影响。 图7 空载正弦位置指令响应曲线Fig.7 Response of the sinusoidal position command with no load 在保持同样的阶跃位置指令输入后,在2 s时给系统施加周期4 s幅值为1 000 N·m的扰动力矩,可得到系统的响应曲线如图9,10所示。 图8 空载正弦位置指令电流响应曲线Fig.8 Cur r ent response of the sinusoidal position command with no load 图9 正弦扰动力矩作用下位置速度响应曲线Fig.9 Position and velocity response curve under sinusoidal disturbance torque 从周期扰动力矩加载实验可以看出,PID算法位置波动范围为0.84~1.15 rad,PID+ESO算法位置波动范围为0.96~1.03 rad,BINTSM+ESO算法位置波动范围为0.997~1.002 rad。从速度变化曲线可看出,在施加周期扰动后,BINTSM+ESO算法速度变化范围始终在零速较小区间范围内变化,而PID+ESO算法速度曲线与零速有较大的偏差值。从以上加载仿真实验电流曲线也可看出,本文所设计的BINTSM+ESO算法电流响应较快,且与其他控制算法相比,电流变化范围一致,未出现滑模控制常见的抖动情况。 图10 正弦扰动力矩作用下电流响应曲线Fig.10 Current response curve under sinusoidal disturbance torque 本文在反步控制理论的基础上,设计了一种双闭环结构的新型双电机同步消隙伺服系统控制方案,在控制器设计过程中引入了积分非奇异终端滑模面,并利用扩张状态观测器对系统未建模动态及扰动进行补偿,仿真实验结果证明: (1)采用反步积分非奇异终端滑模控制理论对双电机同步消隙伺服系统进行设计,能简化系统的控制结构,并提高系统的响应能力;积分非奇异终端滑模面的引入能减小滑模控制常见的抖动问题,采用指令滤波的方式避免了控制器设计过程中求导过程导致的输出控制量过大。 (2)利用扩张状态观测器对系统总扰动进行补偿,增强了双电机同步消隙伺服系统的鲁棒能力,且相较于PID+ESO的扰动补偿方案,本文提出的BINSTM+ESO的控制策略有明显的优越性。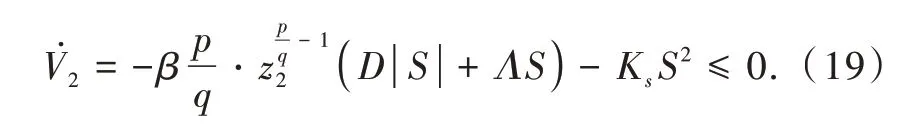

2.3 基于扩张状态观测器(ESO)的扰动补偿







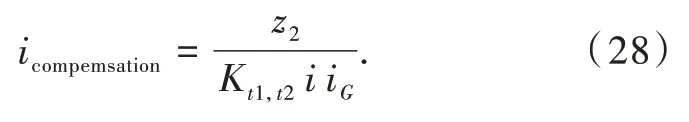
3 系统仿真实验
3.1 系统仿真模型建立

3.2 空载阶跃信号仿真实验


3.3 空载正弦信号仿真实验

3.4 正弦干扰力矩加载仿真实验



4 结论
