大城市交通出行链模型发展路径辨识
——以武汉为例
2022-05-18佘世英李延新向燕陵
郑 猛, 佘世英, 曾 浩, 李延新, 向燕陵
(1.武汉市交通发展战略研究院, 武汉 430017;2.深圳市城市交通规划设计研究中心股份有限公司, 深圳 518000)
0 引言
基于出行的四阶段模型(Trip-based Model,4SM)作为城市交通模型主流架构方法,自1950年代诞生,1980年代末期传入国内,至今已经有近70年历史. 由于其在如何使用不同子模型的行为参数上缺乏稳定性和一致性[1](陈先龙). 很难反映由于社会经济发生变化或科技提升导致的出行需求变化[2](张晓东等),当涉及交通需求管理政策,如出行定价政策的评估时,四阶段法的独立性假设经常被视为致命缺点[3](CuauhtemocAnda等),亟需突破和创新. 国内学者陈必壮等[7]、陈先龙[1]、全波[4-6]、魏贺等[8]、马毅林[9]等围绕交通模型未来发展进行了全面而深入的思考;张天然[10]、赵再先[11]等、Cuauhtémoc, A.等[3]、邓进[12]、陈先龙[13]亦从大数据的角度提出了传统模型改进方法和建议. 随着城市的发展,国内对基于活动的模型研究也日益深入,并将其视为新一代模型发展的重要方向. 李民[14]、宗芳[15]、褚浩然[16]、万涛[17]、王树盛[18]、杨敏[19]、王迎[20],分别从出行方式选择、目的地选择模型、居民出行链特征和需求分析等角度比较系统全面的介绍了国外基于活动的建模理论,从单个子模块或局部算法的角度进行了改进. 隽志才[21]从基于活动方法的协作性限制出发,研究了主要家庭成员活动与出行选择和时间分布之间的相互影响模式. 徐文强等[22]结合随机效用理论,以活动链方式进行网络配流建模. 此后杨励雅[23]对出行方式与出行时间联合选择模型展开了研究、林早[24]则从出行生成—分布组合模型入手展开研究. 但以上研究大多停留在理论层面,鲜有工程实践领域的研究和应用. 文献[25-28]分别从国际交通模型60年发展历程[25]、ABM模型[26]、AgBM模型[27](Agent-based Model)以及大数据在模型中的应用[28]等最新进展进行了全面介绍和剖析. 研究表明,经过近30年的快速发展,美国虽然已经有30余个都市规划组织[6](Metropolitan Planning Organization MPO)开发完成或者正在开发基于活动链的模型(Activity-based Model,ABM),但仍存在诸多障碍,特别是在美国以外的应用仍然非常有限,而我国尚持观望态度[7].
综上所述,四阶段模型在理论上的缺陷以及适应当前城市发展转型在应用方面的局限性已经广为共识,而活动模型代表了今后出行分析技术的发展方向,如何在工程实践领域寻求一条科学可行的现实发展之路是亟待研究突破的重大课题. 本文首先对活动模型的基本概念进行了辨析和分类. 在深入比较四阶段模型、出行链模型和活动链模型这3种典型建模方法基础上,提出了一种基于集计出行链的模型架构方法,并结合武汉实践探索进行了剖析,最后基于武汉市千万人口、3 400余个交通小区和复杂交通场景实证分析,测试了该方法的工程实践可行性和先进特性,以期为国内外同行借鉴和参考.
1 基本概念辨析与模型分类
1.1 基本概念界定
在讨论活动模型的时候,笔者发现,很多概念并未统一. 在英文翻译过程中,不同的学者也各有差异. 如同样是ABM,有翻译为基于活动的模型,也有称之为基于行为的模型;对于出行链和活动链,二者亦常常混淆. 为此,本文首先做如下界定:
活动链(Activity Chain)特指出行者一日活动顺序链接的组合. 出行链(Tour)则表征出行者从某个起点出发,最后回到该起点的一系列出行顺序链接的组合. 因此出行链往往亦等同于活动链. 为以示区别,本文将出行链界定为特指由若干顺序链接的出行所构成的独立往返单元,即1个出行链有且仅有1个主活动和1个独立往返单元. 其中主活动的地点定义为主目的地,主活动之外的其他次要活动地点称之为中途停留点. 每个出行链都由去程和回程2个部分组成. 对于部分出行链,由于在1个统计周期内(如24 h)不能构成完整往返结构(只有去程或者回程),称之为半程出行链(Half Tour). 因此,1个活动链可包含1个或多个出行链,即出行链∈活动链. 出行链在去程或回程过程中可有1个或多个中途停留点,比如基家工作出行链在上班途中(去程)送小孩上学,下班途中(回程)顺便在商场购物后回家. 本文将去程和回程途中均不含停留点的出行链称之为基本出行链.
按照以上的概念界定,实测数据显示,武汉市2020年11—12月共开展1.5万户居民活动出行调查,经过清洗、校核后,筛选出有出行、且以家为初始起点并最终回到家的样本,共统计得到活动链种类344种,出行链类别153种. 从聚类的角度而言,出行链的分类方式较活动链在数量上降低了55.5%. 从有无中途停留点的角度,无停留点的基本出行链样本占比86.9%,较活动链分类方式提升了9.4%. 因此,以出行链为基本单元进行建模比按活动链方式建模可显著降低模型复杂度.
1.2 模型分类浅析
从基于出行的四阶段模型到基于活动的模型,按照演化路径从简单到复杂的顺序来看,大致可划分为混合模型、集计出行链模型、活动链模型和基于智能体的模型四大类,如图1所示.
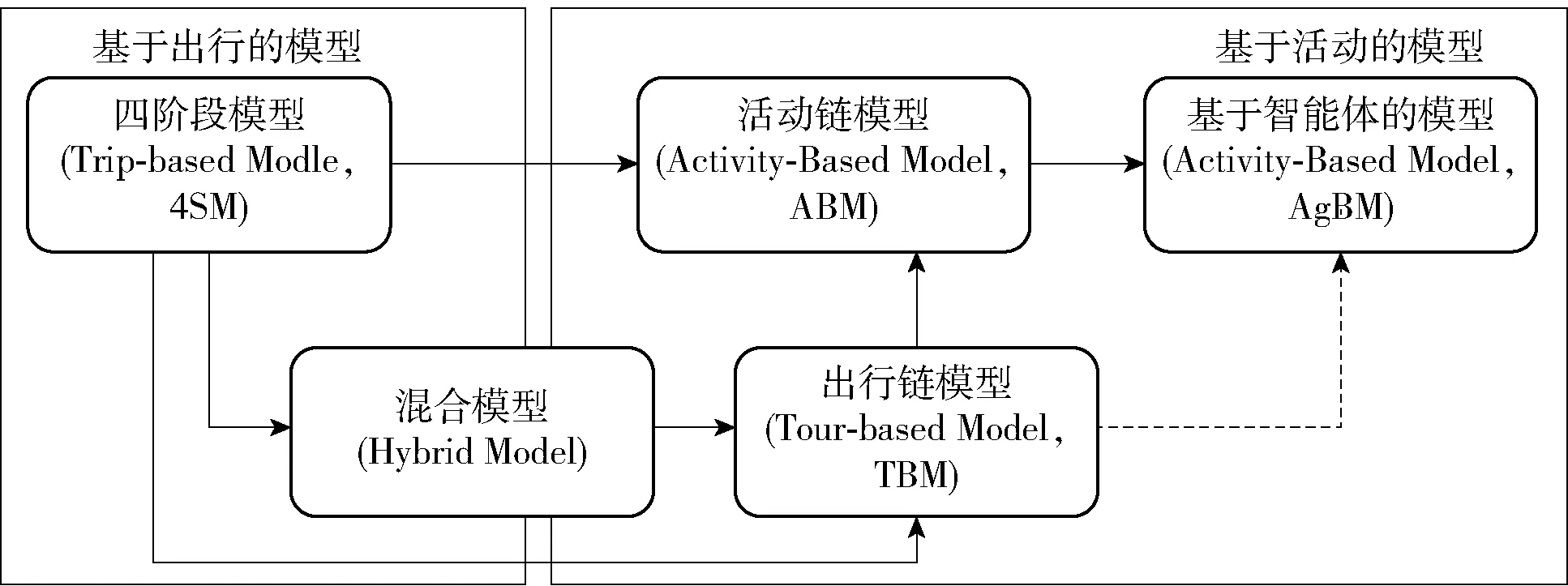
图1 交通模型演化路径及基本分类
为便于理解,以图2为例,假如①为某个体一日实际的活动,其早上07:30从家(H)出发,开车上班(W),途中送小孩上学(C), 07:50离开学校;中午12:25从公司乘地铁去购物(S),13:40乘地铁返回单位;17:30下班后开车回家;晚上19:10乘出租车去大剧院看演出(T),21:15演出结束后乘出租车返回. ②③④分别代表了四阶段模型、出行链模型和活动链模型3种典型的解析方式. 由于AgBM尚属于前沿探索领域,而混合模型创新性不足. 本文重点围绕②③④3种典型模型架构展开剖析.

图2 典型模型架构比较
四阶段模型最为粗糙,仅提取了出行起终点和交通方式这两类要素,以出行(Trip)为基本分析单元,牺牲了时间这一重要的维度,亦割裂了各出行之间的内在联系. 而活动链模型从理论上几乎真实地还原了个体实际活动,但由于模型抽象和计算能力的制约,亦做了适当的简化. 以Bowman和Ben-Akiva提出的日活动计划方法[30-31]为例,其将活动的出发时间用时间段T来代替(T可按小时、15 min或者其他颗粒度划分),活动选择和活动安排则基于不同个体(家庭)的社会经济属性和日活动计划予以制定,其活动目的地在空间上的投射可是交通小区、亦或颗粒度更小微区. 部分模型还考虑了家庭成员之间的相互影响,如家庭只有1辆车,某成员自驾出行,则另外的成员在活动安排和交通方式选择方面就无法选择自驾或者与自驾相关的活动. 这一理论架构和建模方式为精准刻画和研究居民出行行为提供了丰富的要素组合与想象空间. 但活动链模型当前最大的问题是复杂性障碍,除了较高的资金投入、较长的开发周期和精细化的数据基础支撑之外,模型运算时间超长且缺乏收敛机制亦是现实实践中难以推广的主要原因. 如纽约出行链模型最初版本在服务器主机上运行1次需要1周时间, 后来改进后仍然需要3 d时间[29]. 加拿大约克地区ABM模型在Z440服务器(Intel Xeon E5-1603v3、128G内存)上运行1次需要30~35 h[35],这对于仍处于快速发展的大多数国家城市而言,几乎是难以接受的.
出行链模型可视为活动链模型的简化和抽象,其核心思路是将相互链接的活动解析为单个独立的往返出行单元——出行链. 在单个出行链内部,模型保持了出行主体在活动选择、交通方式和出行时间以及关联活动中的一致性,既可采取集计的建模方式(不考虑各出行链之间的相互关系或采取变通的处理方式)以提升运行效率;又可采取非集计的建模方式,从而灵活切换到活动链模型. 因而相比活动链模型,出行链模型具有更大的弹性.
2 出行链模型路径辨识与探索
2.1 出行链模型发展路径辨识
截至目前,较有代表性的出行链模型包括英国交通部支持开发的DIADEM[36]、ATKINS公司团队在英格兰开发的GBMF[37],但均仅仅考虑了基于家的通过PA实现的出行链近似计算,对于非基于家的出行链仍然按照四阶段出行建模;没有考虑出行链往返行程的混合出行方式;没有考虑中间停留点的目的地选择建模;出行主方式只考虑了私家车和公共交通,没有考虑慢行等其他方式. PTV公司在20世纪初亦提出了一套出行链建模方法[38],但缺乏完整清晰的数学定义和描述,模型输出完全是独立的出行Trip,输入出行链结构被打断,无法重构分析整体出行链的行为特征,亦缺乏活动持续时间的定义和描述.
2015年,RSG公司从理论基础、实际应用、政策敏感度3个维度24项指标对四阶段模型、出行链模型(原文表述为混合模型,包含高级四阶段模型、混合出行/出行链模型以及集计出行链模型)和活动链模型(包含非集计出行链模型)3种典型建模方法进行了综合对比,本文进行了量化转换,如表1所示[25]. 分析显示,出行链模型和活动链模型在理论和政策敏感性方面较四阶段模型均有显著优势,充分体现出二者作为替代升级方面的巨大潜力和诱人的前景;而出行链模型的短板主要体现在时间一致性、人的一致性、空间解析度、使用便捷度等方面,这些恰恰反映了当前研究的不足,亦是本文需要着重阐述的关键点.

表1 三种典型模型架构性能对比
2.2 集计出行链模型架构探索
综合考虑前述分析,提出了一种新的集计出行链模型方法(Aggregate Tour-based Mode,ATBM),该方法以基本出行链为分析单元,以人群为对象按照集计的方式进行模型构建,充分考虑各出行链在去程和回程时间、交通方式以及主目的地选择和中途停留点选择的时空制约因素和内在一致性. 总体架构如图3所示,共分为6个部分.
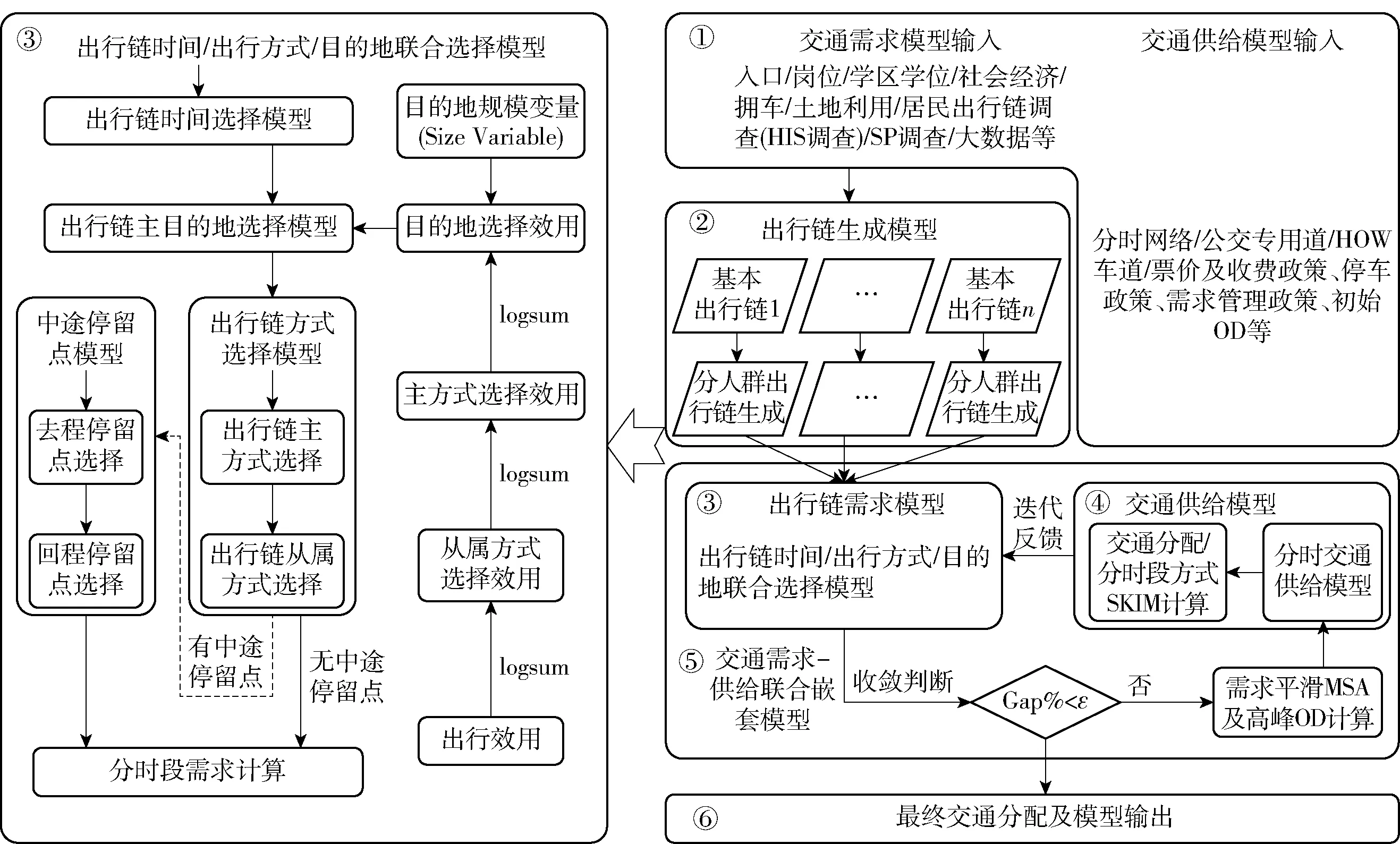
图3 集计出行链的模型系统架构图
第1、 2部分用于模型输入和出行链生成. 基于人口、岗位、学区学位、经济及拥车、土地利用、综合交通调查及大数据等,对人群进行类别划分、在空间层面进行人口合成计算,根据人群和基本出行链,进行交叉分类,得到各交通小区基于“人群+出行链”的生成量. 为提高模型对交通需求管理政策、建成区环境以及慢行交通等敏感性,在交通小区层面,可细致到地块级别、人群分类亦可根据交通需求管理政策对群体的影响进行更细致的类别划分.
在基本出行链的分类方面,共划分为5大类,前3类为基家的出行链,包括基家工作出行链、基家上学出行链和基家其他出行链,后2类分别为基于工作地的出行链和基于其他的出行链(主要针对流动人口和对外集散点建模). 按照从简单到复杂的次序,建模过程中先进行基本出行链建模,然后在此基础上考虑有停留点情形建模. 该分类包含了通勤和通学两大稳态活动单元,以及生活、工作和商旅3个半稳态活动单元,融合了出行链、活动单元和时空约束3个层次的关系. 而基家工作出行链、基家上学出行链等还可基于POI大数据和岗位/学位数据等引入职住、学区空间关系约束,以提高生成阶段的精准度. 对基于其他的出行链,如酒店旅馆、机场火车站等对外枢纽等,多数情形下采取半程出行链的方式. 在确定了对外枢纽、酒店旅馆位置、发生/吸引量之后,同样可采取类似基于家的其他和基于工作地的出行模型方法建模,因而形成完整的出行链模型体系.
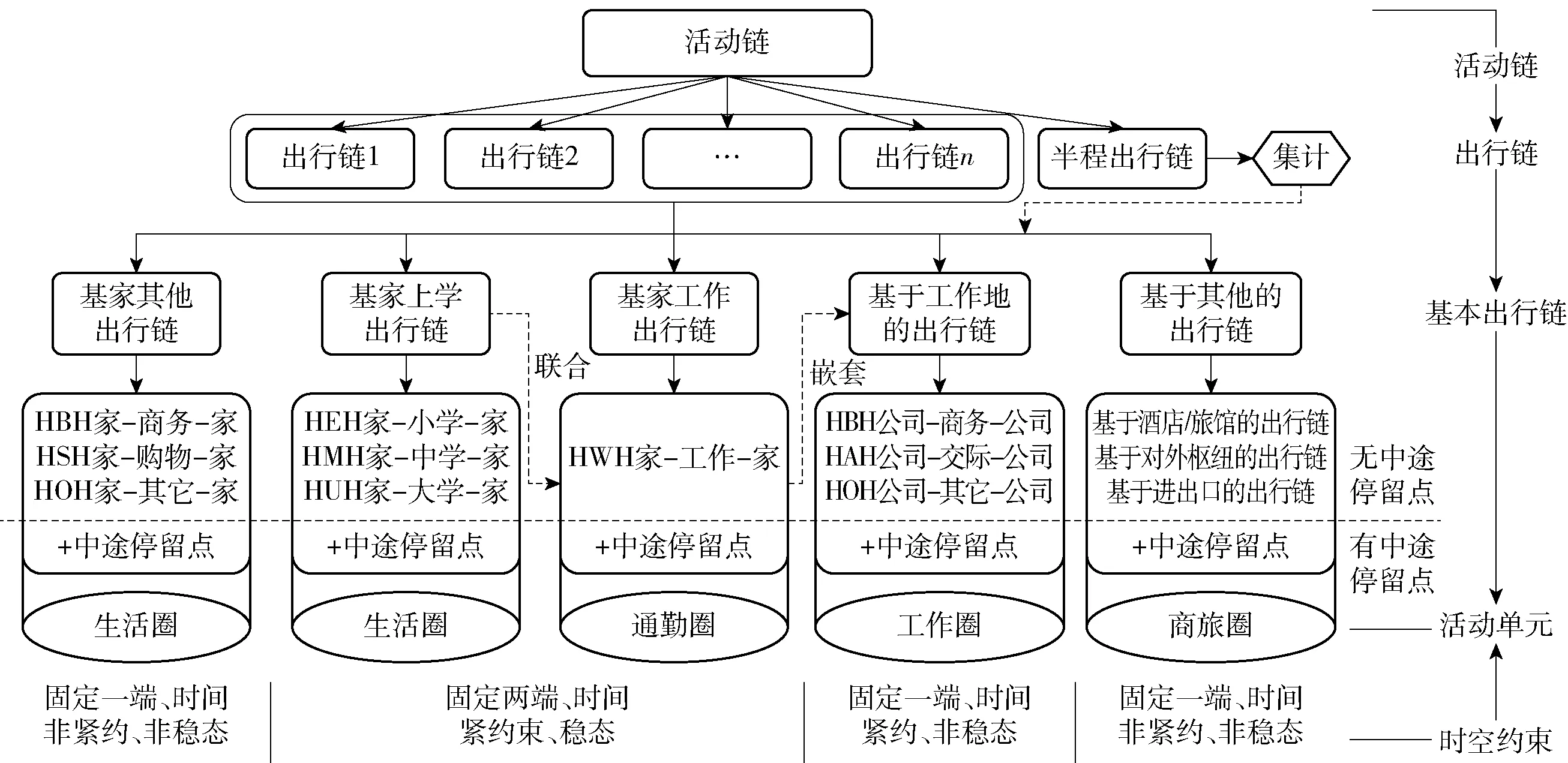
图4 活动链解析与基本出行链分类体系
第3部分侧重于出行链时间、出行方式和目的地及中途停留点联合嵌套选择建模,最右边的分支用于自下而上的可达性对数和,中间的分支用于自上而下的需求计算,最左侧的分支中显示了出行链中往返行程中间停留点建模. 该部分可基于不同的时段划分与“人群+出行链”类别进行并行计算,在去程回程中充分考虑交通方式的可变性、中途停留点的数量及方式等,以灵活适应多种情形. 底层效用除了计算通常的广义阻抗,也可考虑区域差别化停车收费,按照出行链的活动时长分布和用地类型进行细分. 同时,引入距离的对数函数以考虑时间价值随距离增加的阻尼特征. 上层效用计算保证纵向一致, 如目的地选择效用矩阵基于下层方式选择的对数和,并同时考虑土地利用的影响,如基家上班上学出行链采取双约束目的地选择模型,其他出行链适用于单约束目的地选择模型. 出行链时序解析综合考虑了不同人群和出行链组合往返行程时序组合的概率.
第4、5部分分别为交通供给模型和交通需求—供给联合嵌套模型. 第6部分用于出行OD计算、交通分配和模型输出. 其中第5部分通过引入WebTAG供需差距函数(Gap),以检验模型的收敛特性,基于迭代计算和MSA以实现供需模型之间的迭代反馈并确保模型快速收敛至可接受的水平,从而确保模型结果的稳定性. 整个模型架构都可基于Python开发实现,在供给模型阶段调用EMME4等商用软件实现数据交换.
2.3 模型架构特性分析
1)能对基家工作出行链、基家上学出行链、基家其他出行链以及基于工作地的出行链、基于其他的出行链(主要针对流动人口和对外集散点建模)和半程出行链等多种不同类型的出行链进行建模,每一种出行链类别都可进行细类扩增,以灵活适应国内从特大城市到中小城市各类情形. 对于诸如上下班途中接送小孩上学放学等不同出行链的联合与嵌套情形,本模型架构亦可轻松应对和建模. 基于武汉市的实测数据,各出行链分类汇总关系如表2所示.
2)模型充分考虑了出行链去程/回程在时间段上的连续性要求. 模型将全天分为不同的时间段,去程和回程所处的时间段满足先后顺序的约束,并通过参数化的方式使得行程时间易于调整,如表2所示. 以5个时段为例,每个人群和出行链类别分别有15种时序组合,每个时序组合对应于1种活动持续时长分布概率,因而可较为细致地模拟区域差别化的停车收费政策,避免了在出行链的阻抗中直接增加停车费用;亦支持结合出发时间和出行时长对不同的公交出行费用测试,同时从运营效益最大化的角度评估不同收费模式对出行的影响. 在基于区域或境界线的拥堵收费政策研究方面,亦具有更强的分析能力.

表2 武汉市基于出行链的调查统计分析
3)模型充分考虑了出行链去程/回程在方式选择上的连续性/一致性要求. 模型对可变方式出行和不可变方式出行进行了专门的定义. 如,驾驶小汽车设为不可变方式,在回程过程中必须和去程保持一致;任何去程使用可变方式的出行链,在回程阶段不允许切换到驾驶小汽车的方式. 若出行链去程为可变交通方式,则回程基于可变交通方式集合,通过效用对数和以计算其子方式选择概率. 去程和回程交通方式组合示例如表3所示.

表3 出行链往返出行时间段组合关系

表4 出行链中的去程- 回程交通方式组合
4)使用多约束的目的地选择来满足供需平衡:同时使用了可达性变量(下层效用的logsum)和结合用地的规模变量(size variable)作为目的地选择过程中的输入;通过二维矩阵形式的IPF算法(rectangular IPF)实现基家工作出行链的双约束平衡;通过二维方阵形式的IPF算法(square IPF)实现基家上学出行链(小学、中学、大学)的双约束平衡. 而其余出行链则基于单约束机制.
5)对人口和用地规划的支持. 模型只需要对输入的人口分布变量进行调整,即能轻松地对不同人口增长方案进行情景测试;不同规划年的用地特性能方便地通过规模变量嵌入模型并用于测试;由于对出行链的模拟并非基于蒙特卡洛方法(Monte Carlo simulation), 因而不需要进行多次重复运算.
6)支持并行计算和多线程高效运行,实现模型快速收敛. 由于不同类型的出行链之间在模型运算过程中相互独立,在需求计算部分,模型运算使用了多线程以尽可能提升性能. 在需求与供给迭代嵌套模型中,引入差距函数和MSA算法,以加速和平滑模型收敛性能. 差距函数计算如式(1)所示.
(1)
式中,X和C分别代表当前需求矩阵和综合阻抗;D代表经迭代后的下一轮需求更新;ij分别代表交通小区起终点;p代表活动类别;c代表人群类别;m代表交通方式,T代表出行链时段划分.
3 基于武汉市的模型实证分析
基于上述模型架构,本研究以武汉市为例进行了实证分析. 建模范围涵盖全市1 200万人口,8 569 km2用地,共划分交通小区3 476个,其中主城区1 860个(平均0.3 km2/个),如图5所示. 模型考虑了共5个时段15个出行时序组合、五大类出行方式17种去程回程交通方式组合,人群分类按职业、拥车和收入情况分12类,考虑了9种基本出行链类别和68种“人群+出行链”组合. 在供给模型方面,共包含10.8万条路段,4.3万个节点,1 457条公交线路(含轨道、公交、BRT等,分上下行),并结合5个时段交通供给的差异性进行了细致的建模. 经参数标定和模型校核,运行测试显示,在Precision 7 730移动工作站(Intel(R) Xeon(R) E- 2186M,CPU @ 2.90 GHz,RAM128 GB)硬件环境下,需求与供给模型从冷启动迭代达到正常收敛水平(Gap<0.2%),模型整体运行时间约28.1 h,迭代24次;深度测试可继续达到Gap<0.1%的收敛水平,耗时约49.6 h,迭代43次,如图6所示. 测试结果论证了该模型架构的现实可行性,以及模型在收敛性和计算效率方面较ABM模型的优越性. 在实际应用场景下,模型可基于收敛情景为基础进行增量迭代(热启动),单次运行时间约1~1.5 h,因而可显著减少迭代次数和缩短模型收敛时间.
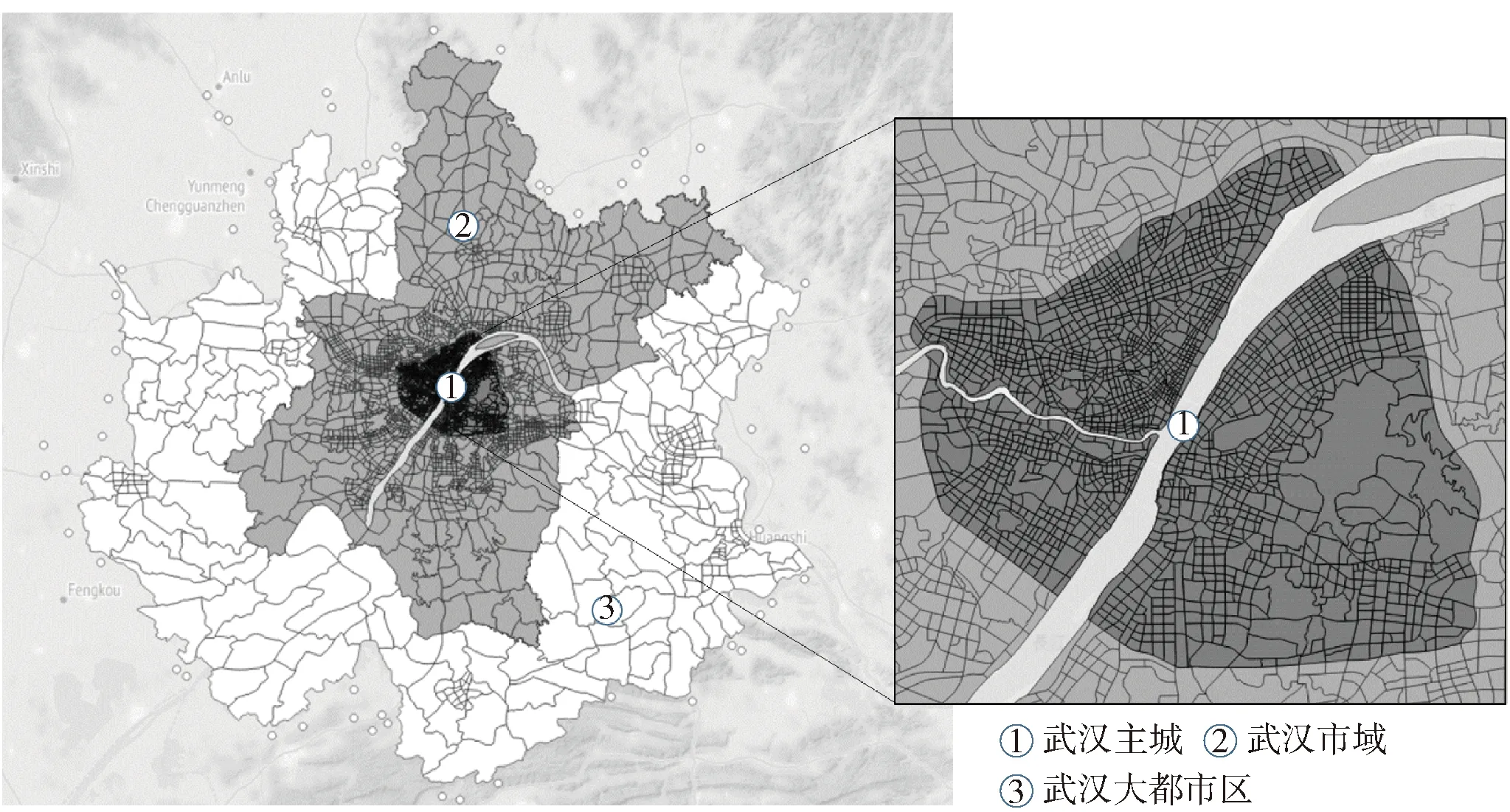
图5 案例城市交通小区划分示意图
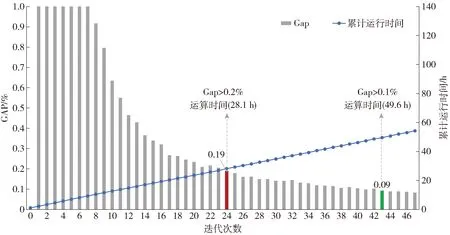
图6 模型迭代及收敛水平、运行时长分析
分别从小汽车燃油费弹性量、公交票价弹性量以及中心区计时停车费用弹性量3种情形进行了模型现实性测试(realism tests)和敏感性测试(sensitivity tests),结果显示:燃油费增长10%后,全市范围总体平均弹性值为-0.17,非刚性需求的弹性量相对较低;公交票价提高10%后,总弹性量为-0.63,基家上学出行链弹性量相对较大. 而按小时收费的停车费率增加10%后,小汽车出行的弹性量为-0.68,且主城区的弹性量为-0.9,高于全市范围的弹性量,模型亦可敏感捕捉到小汽车乘客和驾驶员对停车收费变动的影响. 测试结果亦验证了模型在复杂交通政策方面的良好性能.
4 结论与展望
本文澄清了出行链模型的基本概念,在深入比较四阶段模型、出行链模型和活动链模型这3种典型建模方法基础上,对出行链模型发展路径进行了辨识,提出了一种基于集计出行链的模型架构方法,分析了该模型架构特性,并基于武汉市进行了实证分析. 研究显示:
1)本研究提出的集计出行链模型架构有效性弥补了四阶段模型在出行时间维度的缺失以及方式划分和目的地选择方面内在不一致性,规避了活动链模型在收敛性能、运算效率等方面的应用障碍. 经过实证分析,在千万人口、3 400多个交通小区和复杂交通运行场景下,该模型相比ABM模型具有优越的运算效率和收敛性能. 分别从小汽车燃油费弹性量、公交票价弹性量以及中心区计时停车费用弹性量3种情形进行了模型现实性测试(realism tests)和弹性测试(sensitivity tests),亦验证了模型在复杂交通政策方面的良好性能.
2)集计出行链模型架构有效降低了行为建模的复杂度,具有广泛的适应性和可扩充性. 基于武汉的实际调查来看,在进行出行链拆分以后,共识别出出行链组合153种,其种类较活动链整体下降了55.5%. 且86.9%的基本出行链无中途停留点. 有停留点样本较基于活动链的建模方式下降了9.4个百分点. 因此,本研究提出的以基本出行链为单元进行模型构建可显著降低建模复杂度,同时也确保了在主体特征方面与活动链保持了一致性.
3)出行链需求建模以及需求与供给的迭代和收敛是整个模型框架的核心,模型计算确保了整个过程中出行链的完整性,因而可灵活适应不同“人群+出行链”组合的差异化交通政策分析,以适应当前“以人为本”的规划研究诉求. 对于出行链需求模型达到收敛后,将出行链需求矩阵结合时序选择模型进行分时OD转化,纳入供给模型进行最终交通分配,此步骤在传统四阶段模型中亦相对成熟,可充分发挥既有优势,因而模型易于升级与维护. 由于篇幅的关系,本文对集计出行链核心算法、模型校核校验及参数标定未做详细解析,这些都有待于后续研究予以充实和扩展.
