鲁西牛生长发育规律研究
2022-05-18张珂菁成海建姜富贵宋恩亮蓝贤勇
毕 谊,张珂菁,成海建,,陈 宏,姜富贵,宋恩亮,蓝贤勇*
(1.西北农林科技大学动物科技学院,陕西 杨凌 71200;2.山东农科院畜牧兽医研究所,济南 250100)
我国养牛业历史悠久,养牛遍及全国各地,其中黄牛数量最多,分布面积最广[1-2]。鲁西黄牛是我国著名的役肉兼用品种之一,具有许多国外某些品种不可比拟的特征和特性[3-6]。除体躯高大、役用能力强、适应性好外,还具有肉用性能好、皮薄肉细嫩鲜美、早熟等特点,而且鲁西牛的屠宰指标甚至接近国外一些著名的肉牛品种指标。目前,鲁西牛牛主产区为菏泽地区和济宁市西部,具有发展畜牧业的优势[7-10]。
体尺指标与家畜的生理机能、生产性能、抗病力以及对外界生活条件的适应能力等密切相关。研究牛的生长发育规律便于养殖场制定科学合理的饲养管理方案,同时有助于更好地组织生产和管理,并指导选种和选配[11-14]。本研究对鲁西牛的体重与各体尺性状间进行相关性分析和通径分析,并建立体重与各体尺间的最优回归模型,期望为后续鲁西牛生长发育方面的改良工作提供科学资料。
1 材料与方法
1.1 样品采集及数据整理
试验选取鲁西牛为研究对象(n=51),所有试验牛均处于相同的生长环境,且处于健康状态。根据采样时间,将试验牛分为群体I(2012年11月采集于菏泽地区牛场,n=32)和群体II(2021年8月采集于菏泽地区牛场,n=19)。其中,群体I中的试验牛包含体尺性状如体重(Y),体高(X1),体长(X2),胸围(X3),管围(X4),腹围(X5),头部(X6),鬐甲(X7),肩部(X8),腰部(X9)和肩厚(X10)。群体II包含体尺性状如体高(X1),胸围(X3)和腹围(X5)。
1.2 数据分析
根据群体I的鲁西牛体尺性状数据,利用SPSS 26.0软件中的Pearson法计算所有鲁西牛体尺性状间的相关系数,并统计其平均值,标准误差和变异系数。以体重Y为因变量,体高(X1),体长(X2),胸围(X3),管围(X4),腹围(X5),头部(X6),鬐甲(X7),肩部(X8),腰部(X9)和肩厚(X10)为自变量进行通径分析,利用Excel 2022解析多元一次方程组,并分解体重与各体尺性状间相关系数。利用SPSS 26.0软件对体重与个体尺性状进行逐步回归分析,构建最优回归模型。紧接着,根据鲁西牛群体I得到的最优回归模型及群体II的体尺性状预测其体重。最后,合并鲁西牛群体I和群体II为群体III,统计其表型数据,并进行相关性分析和通径分析。
2 结果与分析
2.1 鲁西牛群体I表型数据统计及各体尺间相关性分析
利用SPSS 26.0统计鲁西牛群体I表型数据(n=32),并分析其平均值和标准误差。根据其平均值与标准误差分析总体平均值相关的变异程度,结果(表1)显示,体重(Y)、体高(X1)、体长(X2)、胸围(X3)、管围(X4)、腹围(X5)、头部(X6)、鬐甲(X7)、肩部(X8)、腰部(X9)和肩厚(X10)的变异系数分别为19.45%,4.39%,7.80%,6.36%,3.06%,8.03%,17.13%,21.12%,13.41%,15.74%和21.12%。
鲁西牛各体尺性状间相关性分析结果(表2)显示,所有体尺性状均与体重间存在显著相关性(P<0.05),其中头部与体重呈负相关,其余性状均与体重呈正相关。根据相关程度由大到小排序为X3>X5>X7>X8>X10>X1>X6>X4>X2>X9,体重与胸围和腹围相关程度最高,相关系数分别为0.911和0.904。
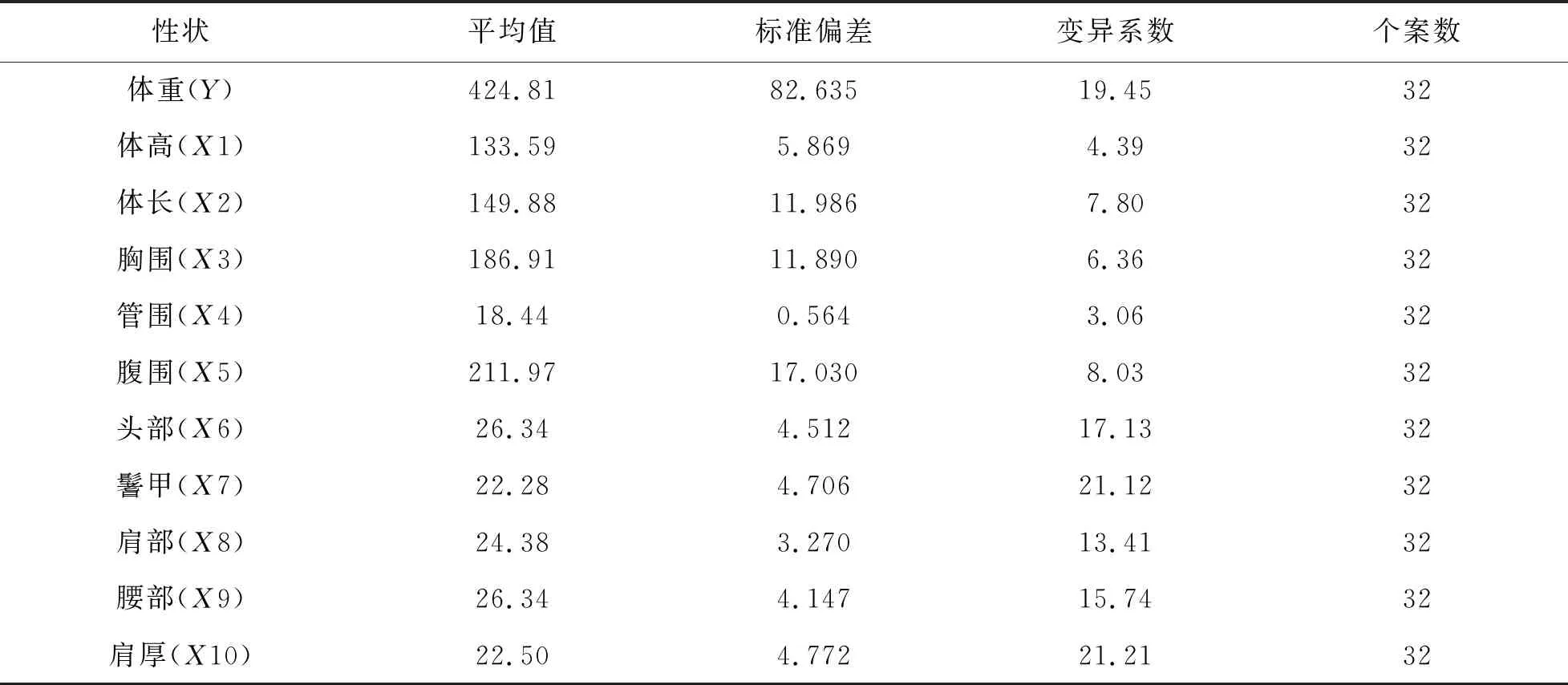
表1 鲁西牛群体I表型数据统计
2.2 鲁西牛群体I体重与各体尺性状的通径分析
对鲁西牛群体I中的体重和各体尺性状间进行通径分析,得到以通径系数(P)为变量的多元一次方程组如下。
0.536=P1+0.556P2+0.546P3+0.318P4+0.312P5-0.434P6+0.401P7+0.328P8+0.152P9+0.064P10;
0.433=0.556P1+P2+0.364P3+0.223P4+0.470P5-0.548P6+0.431P7+0.084P8+0.292P9+0.118P10;
0.911=0.546P1+0.364P2+P3+0.477P4+0.846P5-0.521P6+0.610P7+0.576P8+0.343P9+0.590P10;
0.493=0.318P1+0.223P2+0.477P3+P4+0.444P5-0.365P6+0.268P7+0.205P8+0.209P9+0.299P10;
0.904=0.312P1+0.470P2+0.846P3+0.444P4+P5-0.475P6+0.638P7+0.546P8+0.456P9+0.617P10;
-0.521=-0.434P1-0.548P2-0.521P3-0.365P4-0.475P5+P6-0.547P7-0.094P8-0.100P9-0.254P10;
0.628=0.401P1+0.431P2+0.610P3+0.268P4+0.638P5-0.547P6+P7+0.555P8+0.312P9+0.603P10;
0.616=0.328P1+0.084P2+0.576P3+0.205P4+0.546P5-0.094P6+0.555P7+P8+0.254P9+0.566P10;
0.413=0.152P1+0.292P2+0.343P3+0.209P4+0.456P5-0.100P6+0.312P7+0.254P8+P9+0.341P10;
0.569=0.064P1+0.118P2+0.590P3+0.299P4+0.617P5-0.254P6+0.603P7+0.566P8+0.341P9+P10。
随后,对多元一次方程组求解得到如下通径系数:P1=0.226,P2=-0.107,P3=0.211,P4=0.025,P5=0.622,P6=-0.091,P7=-0.065,P8=0.106,P9=0.035,P10=-0.004。
2.3 鲁西牛群体I的体重与体尺性状相关系数分解
对相关系数进行分解,结果显示腹围对体重的直接作用最大(P=0.622),体长对体重的直接作用最小(P=-0.107)。各体尺性状的直接作用由大至小排序为腹围(X5)>体高(X1)>胸围(X3)>肩部(X8)>腰部(X9)>管围(X4)>肩厚(X10)>鬐甲(X7)>头部(X6)>体长(X2)。各体尺性状的间接作用由大至小排序为胸围(X3)>鬐甲(X7)>肩厚(X10)>体长(X2)>肩部(X8)>管围(X4)>腰部(X9)>体高(X1)>腹围(X5)>头部(X6)。综上,腹围通过较强的直接作用影响体重,而胸围和鬐甲则通过与其他体尺性状间较强的间接作用影响体重(表3)。

表3 鲁西牛群体I个体体重相关系数分解
2.4 鲁西牛群体I的体重与各体尺间最优回归模型建立
利用SPSS 26.0进行逐步回归分析,将自变量逐个引入,保留经检验后显著的自变量。同时,引入新变量后,对旧的自变量逐个检验,剔除偏回归平方和不显著的自变量。最后建立最优多元线性回归方程。得到体重与各体尺性状间的最优回归方程为:
Y=2.374X1+2.455X3+2.721X5-923.527(R=0.955),且该方程达到极显著水平(P<0.01),具有统计学意义(表4~6)。
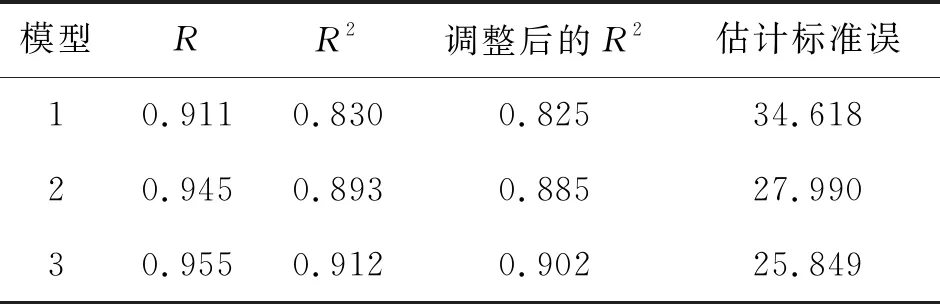
表4 鲁西牛群体I的各体尺性状对体重回归模型摘要

表5 鲁西牛群体I的各体尺性状对体重回归模型方差分析

表6 鲁西牛群体I的多元回归系数的参数估计值检验
2.5 鲁西牛群体II的表型统计及相关性分析
根据最优回归方程以及鲁西牛群体II的体高、胸围和腹围表型数据,预测其体重,并剔除预测出体重为负值的个体。随后将鲁西牛群体I和群体II合并为鲁西牛群体III(n=50),得到结果如下。其中,鲁西牛群体III体重的平均值为451.26 kg,变异系数为20.33%。体高、胸围和腹围的变异系数分别为6.73%,10.91%和11.42%(表7)。分析各体尺性状间的相关性发现,胸围与体重间相关系数最大,相关系数为0.922。根据相关程度由大至小排序为:胸围(X3)>腹围(X5)>体高(X1)(表8)。

表7 鲁西牛群体III的表型数据统计

表8 鲁西牛群体III的表型性状间相关性分析
2.6 鲁西牛群体III的体重与各体尺性状间通径分析及相关系数分解
对群体III中体重与各体尺性状间进行通径分析,建立多元一次方程组,并求解通径系数(P)。
0.630=P1+0.826P2+0.688P3
0.922=0.826P1+P2+0.886P3
0.903=0.688P1+0.886P2+P3
P1=-0.369P2=0.939P3=0.325
随后,根据各体尺性状间的相关系数及直接通径系数对相关系数进行分解,结果显示与体重相关程度最高的胸围性状对体重的直接作用最大(P=0.939),与体重间相关系数最小的体高则是通过较强的间接作用影响体重。详细地,根据对体重的直接作用由大至小排序为:胸围(X3)>腹围(X5)>体高(X1)(表9)。

表9 鲁西牛群体III的个体体重相关系数分解
3 讨 论
体尺指标直接反映家畜的体格大小和体躯结构、发育等状况,也间接反映畜体组织器官的发育情况及体重,它与家畜的生理机能、生产性能、抗病力以及对外界生活条件的适应能力等密切相关。因此,对具有优良体尺性状的牛进行选育一直是肉牛育种工作中至关重要的一环。本研究首先对鲁西牛群体I的体尺性状的表型数据进行统计,并计算标准差和变异系数,结果显示体重、头部、鬐甲、肩部、腰部和肩厚的变异系数均大于10%,属于中度变异。表明这些性状的变异幅度较大,具有较大的选择潜能;其余性状变异幅度较小,均属于弱变异。
皮尔逊相关系数是两个变量的协方差与它们的乘积之间的比率标准差,可以衡量两组数据之间的线性相关性。本研究分析各体尺性状与体重间的相关性,结果显示胸围和腹围与体重相关性最高,相关系数分别高达0.911和0.904,且为极显著正相关。除胸围和腹围外,其余性状均与体重呈显著相关(P<0.01),腰部与体重的相关系数最小。以上结果表明,不同的体尺与体重存在不同程度的相关性,同时胸围与腹围性状与体重密不可分,后续可作为优良生长性状的鲁西牛群体选育时的重要参考依据,集中选择具有较优胸围和腹围表型的鲁西牛进行培育。
通径分析是通过对自变量和因变量之间的相关分解来研究因变量或性状的相对重要性的一种技术[15-16]。而通径系数则是是变量标准化后的偏回归系数,表示变量间因果关系程度的一个指标。本研究将体重与其他体尺性状进行通径分析发现腹围对体重的直接通径系数最大,说明该性状通过较强的直接作用影响体重,其次是体高。该结果提示加强对腹围和体高表型优良的鲁西牛进行选育可能直接影响鲁西牛的体重。同时,笔者发现胸围与体重间间接通径系数最大,这表明胸围可能通过影响其他体尺性状从而对体重发挥较强的间接作用。除此之外,鬐甲、肩厚和体长性状均发挥较强的间接作用。综上,笔者发现与体重间相关程度最高的两个性状同时通过较强的直接作用影响体重,在后续鲁西牛选育过程中可作为重点考虑因素。
最优回归模型指从可供选择的所有变量中选出对Y有显著影响的变量建立方程,且在方程中不含对Y无显著影响的变量,最后求解方程建立的模型。经分析,本研究得到鲁西牛体重与各体尺性状间最优回归模型:Y=2.374X1+2.455X3+2.721X5-923.527(R=0.955),且达到极显著水平(P<0.01)。与前面结果一致的是,引入最优回归模型的变量中包含腹围和体高,这两个性状与体重相关程度最高,且对体重的直接作用最强。除此之外,最优回归模型中还引入了胸围性状,该性状通过较强的间接作用影响鲁西牛体重。根据最优回归模型,笔者推测腹围、体高以及胸围可以作为影响鲁西牛体重的主要因素和选育过程中的重要筛选指标。
根据最优回归模型以及鲁西牛群体II的体高、胸围和腹围表型数据,对鲁西牛群体II的体重进行预测。随后,将鲁西牛群体I和群体II合并为鲁西牛群体III,并统计其体重、体高、胸围和腹围表型数据,进行相关性分析及通径分析。结果显示,鲁西牛群体III的体高、胸围和腹围均与体重呈极显著正相关,相关程度由大至小排序为:胸围>腹围>体高。对相关系数进行分解结果显示,胸围对体重直接作用最强,其次是腹围和体高,该结果与鲁西牛群体I的分析结果不完全一致,这可能由于样本量不同导致。但以上结果均可表明:体高、胸围和腹围体尺性状可以作为后续鲁西牛育种过程中重要3个参考体尺指标。为此,本研究为后续合理提升鲁西牛生长发育性能提供科学资料。
