基于滑模变结构控制多机器人协同编队的研究综述
2022-05-18胡凯陈旭杨平化杨立帆胡永赞
胡凯 陈旭 杨平化 杨立帆 胡永赞
0 引言
随着社会和科技的进步,多机器人系统在众多领域获得到了广泛应用.与单个机器人相比,编队协作的多机器人系统具有更好的稳定性,各单体机器人携带的传感器将采集到的信息进行共享互补,加强了机器人的环境识别能力.另外,多机器人系统能够针对不同任务需求组成特定的队形,充分发挥出每个机器人的潜能[1].
对于多机器人的编队控制结构,一般是基于分布式控制设计的[2],包括领航-跟随法[3]、虚拟结构法[4]、基于行为法[5]、图论法[6]、人工势场法[7]等,其中,领导者-跟随法由于简单性和可扩展性成为了工程中最理想、最受欢迎的编队控制策略.在领航-跟随策略下,目前,常用的机器人控制算法有PID[8]、反馈线性化[9]、模型预测控制[10]等,但这些方法都难以调整系统参数,也无法处理系统中存在的非线性约束问题.相对于以上方法而言,滑模变结构控制(Sliding Mode Variable Structure Control,SMC)具备较快的响应速度,对参数不确定性和对外界扰动也具有良好自适应性、鲁棒性,并且更易于理解和实现,因此,在解决典型非线性、强耦合、时变性的多机器人协同控制问题中,SMC具有巨大的潜力和应用价值.
20世纪50年代,Utkin和Emelyanov首次提出了滑模变结构控制的概念.1983年,Slotine等[11]首次采用滑模控制原理设计出机器人的滑模变结构控制器,随后国内外出现大量关于机器人滑模变结构控制的研究.1991年,Utkin等[12]利用SMC原理提出了经典的机器人路径避障策略,这为以后SMC在多机器人协同控制中的应用打下了基础.SMC在多机器人协同编队中的研究可以分为两方面:一是基于常规SMC的编队控制研究;二是基于SMC和其他控制方法结合的编队控制研究.在SMC发展初期,大多数的SMC控制器是基于线性滑模面设计的,但线性滑模面一般只适用于对速度和精度要求不高的非线性系统,而对于多机器人这类复杂的非线性系统,线性滑模面存在明显的缺陷.后来,很多学者提出了以终端滑模、积分滑模等非线性滑模替代传统线性滑模的方案,保证了系统状态在有限时间收敛至平衡点.2018年,Wu等[13]针对具有不确定性的多移动轮式机器人系统,提出一种基于积分终端滑模的编队控制方法,实现了有限时间内多机器人的编队控制和轨迹跟踪.
以往的研究大多是基于运动学或动力学模型实施一般的滑模变结构控制,而在实际编队控制过程中,由于多机器人系统参数的不确定以及外界环境的影响,很难建立精准的运动学或动力学模型,并且SMC本身控制律的不连续性容易引起抖振现象,从而降低了控制性能.针对上述问题,Lian等[14]提出了一种基于径向基函数(Radial Basis Function,RBF)神经网络的滑模控制方法,削弱了滑模控制固有的抖振,提高了多机器人轨迹跟踪的精度.2018年,Huang等[15]针对神经网络不能很好地利用已有经验知识的缺点,提出了一种基于模糊神经网络的自适应滑模控制方法.模糊神经网络(Fuzzy Neural Network,FNN)结合了模糊控制与神经网络控制两者的优势,不仅具有神经网络自学习和快速并行处理的能力,还具备了模糊控制系统充分利用先验知识、以较少规则数来表达知识的优势,这种基于FNN的滑模控制器能够对多机器人模型的不确定性部分、时变外部扰动以及建模误差进行在线估计.此外,随着神经网络层数的加深,优化函数容易陷入局部最优解,并且“梯度消失”现象更加严重,基于RBF等传统神经网络的滑模控制方法越来越不能胜任于高度非线性的多机器人系统.
近年来,深度学习和强化学习得到了深入发展,不少学者尝试将深度神经网络(Deep Neural Network,DNN)与SMC相结合并应用于多机器人的协同控制.2018年,Cui等[16]设计了一种基于DNN的滑模跟踪控制器,通过深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法对抖振抑制控制器中的神经网络进行训练,在无需动力学模型的情况下保证了机器人的轨迹跟踪.在此基础上,Wang等[17]于2019年又提出一种基于DDPG的滑模编队控制策略,实现了在不同速度下多自主水下机器人(Autonomous Underwater Vehicles,AUVs)的协同控制.总之,伴随控制学科、人工智能等技术的快速发展,基于神经网络、模糊逻辑、鲁棒自适应等智能控制与SMC结合的控制器应运而生,利用智能控制的自学习、自适应、自组织等特性可使得SMC根据系统状态自动调节其控制输出,从而有效削弱抖振的影响,并且这些方法之间本身就具有较强的互补性,利用彼此的优势来改善各自缺点,这对提高多机器人协同编队控制的质量具有重要意义.本文按照结构框架在第3章详细介绍基于智能SMC的编队控制方法,特别是DNN与SMC的结合,这是当下和今后的研究热点.
1 滑模变结构控制简介
滑模控制是变结构控制的一个分支,变结构控制也称为滑模变结构控制.需要指出的是,并不是所有的变结构控制都是滑模控制,而滑模控制是变结构控制中主流的设计方法.
滑模变结构控制是一类特殊的非线性控制,其非线性表现为控制作用的不连续性.这种控制策略与其他控制策略的区别在于系统的结构并不固定.该控制特性可以迫使系统的状态被限制在某一子流形上运动,即所谓的“滑动模态”运动(滑模运动).这种滑动模态可以根据实际情况的不同而自行设计,且其与控制对象的参数及扰动无关,也使得处于滑模运动的系统具有很好的鲁棒性.此外,SMC还具有良好的暂态性能、快速响应、对参数变化和外部干扰(噪声等)不敏感等特点,适用于典型的非线性系统、多输入多输出系统,因此,SMC被广泛应用到各种工业控制对象之中.
1.1 SMC的起源发展
20世纪50年代,针对二阶线性系统的研究对象,苏联学者Utkin和Emelyanov首次提出了变结构控制的概念.20世纪60年代,关于SMC的研究主要集中在高阶线性系统在线性切换函数下控制受限与不受限及二次型切换函数的情况,虽然研究对象扩大到了高阶线性系统,但其仍然局限于单输入单输出的系统.20世纪70年代,Utkin又系统地提出变结构控制和滑模控制的方法.此后,对于SMC的研究兴趣急剧上升,并在70年代之后,伴随大规模集成电路、计算机信息技术的飞速发展,SMC相关理论也取得了长足的进步,所涉及的研究对象从简单的线性系统进入到连续与离散系统、确定性与不确定性系统、集中参数与分布参数系统等各种复杂的系统.20世纪80年代后期,SMC理论引起了国内学者的重视.我国高为炳院士首次提出了滑模趋近律和自由递阶的概念,而SMC存在一个显著的问题——抖振问题,趋近律则是一种有效抑制抖振问题的方法.90年代末,高为炳[18]还提出了通过调整趋近律的参数k和e,来保证滑动模态到达过程中的动态品质,并能够减弱控制信号的高频抖动.另外,姚琼荟等[19]、胡跃明[20]、刘金琨等[21]同样为我国SMC理论的研究和推广做出了不可或缺的贡献.
1.2 SMC的控制原理
1.2.1 滑动模态
1)当系统运动点运动到切换面s=0附近时,穿越此点而过,该点称为“通常点”,图中点A就是一个通常点;
2)当系统运动点到达切换面s=0附近时,向切换面的该点的两边离开,此点称为“起始点”,图中点B就是一个起始点;
3)系统运动点到达切换面s=0附近时,从切换面的两边趋向于该点,该点称为“终止点”,图中点C就是一个终止点.

图1 切换面上的3种特性Fig.1 Three characteristics of the switching surface
其中,只有终止点具有特殊的意义.当在切换面上某一区域内所有点都是终止点,则一旦状态点趋近于该区域,就会被“吸引”进该区域内运动.此时,在切换面s=0上所有的运动点都是终止点的区域被称作为“滑动模态”区域,系统在滑模区中的运动叫做“滑模运动”.按照滑动模态区域上的运动点都必须是终止点这一要求,当状态点到达切换面附近时,必然存在以下条件:
(1)
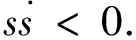
(2)
满足上述到达条件,状态点将向切换面趋近,切换面为终止点区.
1.2.2 SMC的数学定义
设控制系统状态方程为
(3)
需要确定切换函数s(x)求解控制函数u:
(4)
当s(x)=0时,其就是所谓的滑模面.u+(x),u-(x)分别为滑模面左、右两侧的控制器,由控制函数可以看出变结构控制主要体现为u+(x)≠u-(x).因此,滑模变结构控制的本质是通过切换开关使得闭环控制系统具有不同的结构,并且具备渐近稳定等良好的动态品质.
滑模变结构控制系统的响应由趋近阶段、滑动阶段和稳态阶段组成.因此,满足以下3个条件的控制才称之为滑模变结构控制:
1)满足可达条件,即系统状态在有限时间内被驱使到滑模面上;
3)滑动模态具有渐近稳定等良好的动态品质.
1.3 滑模面的设计
滑模变结构控制通常要求具有理想的滑动模态、良好的动态品质和较高的鲁棒性,在理论上这些性能可以通过选择适当的滑模面来实现.在滑模变结构控制发展初期,其研究大部分基于线性滑模面设计[22].典型线性滑模面的设计如下:
(5)
其中,x表示系统的状态向量,C是一个常数矩阵.线性滑模面的滑模变结构控制将系统的整个滑模运动分成了2个阶段:趋近和滑模.趋近阶段是系统从任意初始状态趋向切换面直至到达切换面的过程;滑模阶段是系统在滑模面上的运动过程.当系统到达滑模段后,跟踪误差会渐近地收敛至零,其收敛速度可通过选择常数矩阵C来改变.但不管怎样变化,系统的状态跟踪误差都不能在有限时间内收敛至零.
1.4 抖振问题
抖振现象(图2)是SMC存在的最显著问题,其主要是由时间滞后开关、系统惯性及测量误差等因素引起的,使得系统在滑动模态下产生小幅度、高频率的振动.抖振问题不仅会影响到控制的精度,而且可能激励起系统中高频未建模动态,破坏系统的稳定性.
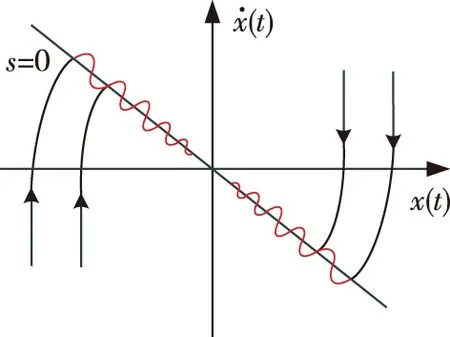
图2 抖振现象(红色曲线部分)Fig.2 Chattering phenomenon (red curves)
对于抖振问题,传统的解决手段主要包括连续函数近似法[23]、边界层设计法[24]、趋近律法[25]、滤波法[26]、动态滑模法[27]等.这些方法虽然对削弱抖振问题具有积极的作用,但每种方法也都有自身的缺点.一方面,它们在运用时具有一定的局限性,比如最常见的趋近律方法,在面对不确定性及干扰较大的情况下,其抑制抖振效果较差;另一方面,以上方法在抑制抖振的同时,也会让控制系统失去部分鲁棒性能.因此,如何既保证非线性控制系统的良好鲁棒性,又能够抑制抖振的影响,是对基于SMC多机器人编队研究的一个主要挑战[28].
2 基于SMC的多机器人协同编队
2.1 多机器人编队
多机器人编队控制是指由多个机器人组成的团队在向特定目标或方向运动的过程中,能够保持预定的队形,同时适应环境约束的控制问题.编队控制问题最初的灵感来源于动物中的鱼群、鸟群等自然现象,其在工程中应用很广泛,诸如无人机的编队飞行(图3)、无人车队的协调控制、无人艇的编队等.

图3 数百架无人机组成的编队表演Fig.3 Formation performance of hundreds of drones
近20年来,自主水下机器人(AUV)的运动控制问题在海洋工程和多机器人协同控制领域引起了广泛的关注.AUV不仅能够克服恶劣的水下环境,而且具有体积小、质量轻、成本低等诸多优点,在资源勘探、海洋监测、救援行动、反潜作战等多方面都有应用.在这些应用中,由于编队控制可以极大地提高多AUV的工作效率,降低实际成本,增强控制系统的鲁棒性,因此通过多AUV的协作来执行任务是具有重要实际效益的.
研究多AUV编队控制,首要需要对AUV的运动学和动力学模型进行分析.机器人的运动学分析主要研究机器人在运动过程中空间几何位置随运动的关系,动力学分析主要分析机器人的运动与受力之间的关系(图4).运动学分析和动力学分析是研究机器人运动的基础,也是控制机器人运动的基础.AUV一般的运动学和动力学模型,如下所示:
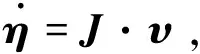
(6)
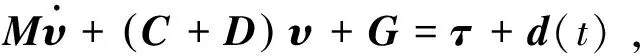
(7)
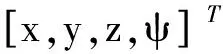
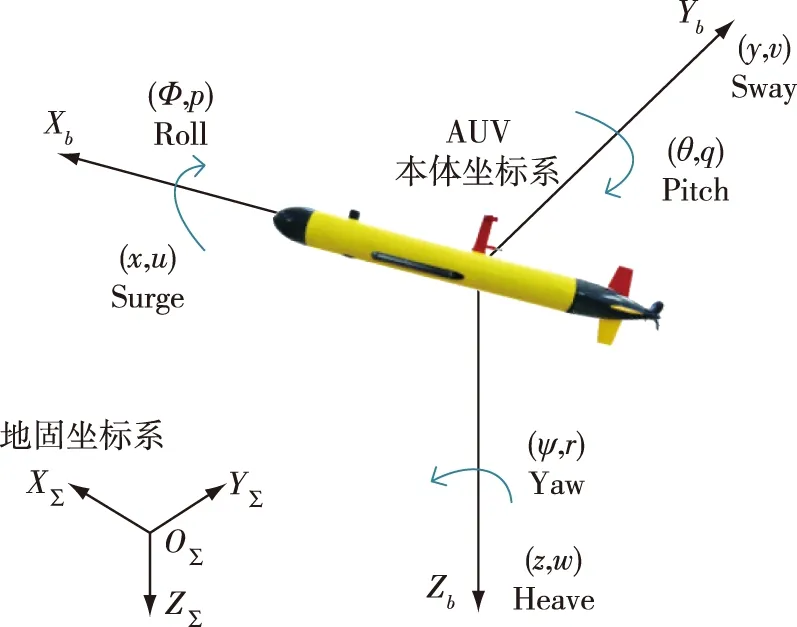
图4 AUV的坐标定义和运动变量Fig.4 AUV coordinates and motion variables
2.2 基于SMC的编队控制
由于多水下航行器是三维空间中高度非线性、耦合和时变的动态系统,并且水动力系数和外部扰动总是不确定的,这给多AUV编队控制带来了挑战.而SMC对模型不确定性和环境扰动具有较好的鲁棒性,近年来在多AUV编队控制中得到了广泛的应用[29-31].当多个AUV以编队的方式进行水中勘察等任务时,需保持期望的姿态,并遵循一定的轨迹,以便后续任务能够顺利进行.
姿态同步是指每个AUV根据控制协议,利用自身和其他AUV在交互过程中获得的信息来调整自己的姿态,使系统中所有AUV的姿态都达到期望的状态.在采用领航-跟随编队结构时,可将AUV的定点定位问题描述为利用控制律使AUV稳定到目标位置和目标姿态.2017年,Zhang等[32]基于SMC原理提出了一种分布式姿态同步控制协议的李雅普诺夫方法,其不仅虑到AUV动力学模型的不确定性以及未知的外界干扰等因素,并且能够使得所有AUV能够协调地跟踪所需的姿态信息,而所需的姿态信息只需由一个或一个子集的AUV即可实现.但以往的研究未考虑到水下存在的通信时延这一因素.针对这一问题,2018年,Liu等[33]设计了一种分布式积分滑模控制器,不仅能够实现通信时延下的AUV姿态跟踪,并且相对于一般滑模控制器,该自适应积分滑模控制律不需要知道外部干扰的上界,符合实践中干扰往往是未知的情况.文献[33]所设计的积分滑模曲面如下所示:
(8)
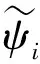
同样,轨迹跟踪问题也是AUV编队控制中的一个研究热点.SMC对建模不确定性和外部干扰具有较强的鲁棒性,因而在水下航行器的轨迹跟踪中具有良好的控制效果.但由于滑模流形的渐近收敛性,一般的滑模控制不能保证跟踪误差在有限时间内收敛至零.此外,在水下进行轨迹跟踪控制时,SMC控制器的收敛速度是一个重要指标,然而一般的滑模控制方法只能通过以大量控制输入为代价来实现,这可能会导致推进器的饱和,在实际应用中是非常不可取的.针对上述问题,2019年,Qiao等[35]提出一种快速非奇异终端滑模控制(SOFNTSMC)方案,与一般SMC方法相比,这种基于SOFNTSMC的轨迹跟踪方法具有更快的收敛速度.所谓终端滑模是指在线性滑模面的基础上引入非线性函数,当系统在控制作用下运行至滑模面上,它能够让被控系统状态在有限的时间内到达平衡点,实现系统状态的有限时间收敛.Qiao等[35]所提出的新型终端滑模面设计方案,不仅能够提升滑模面的性能,同时也避免了奇异问题.终端滑模面的一般设计和SOFNTSMC方案中滑动流形(滑模面)的设计如下所示:
s(x)=x+βxq/p,
(9)
(10)
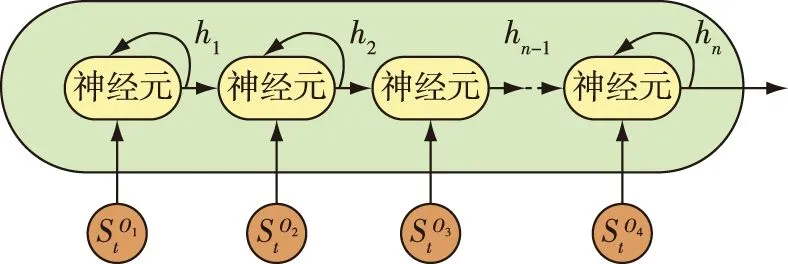
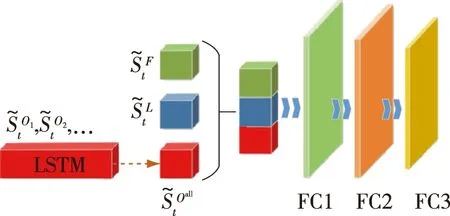
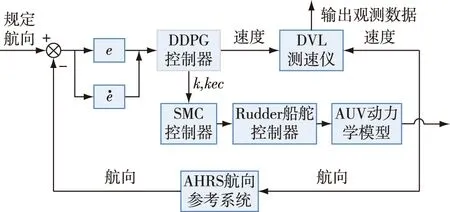
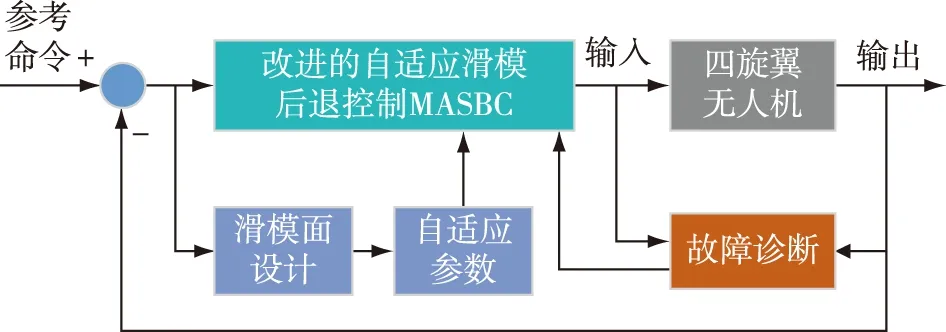
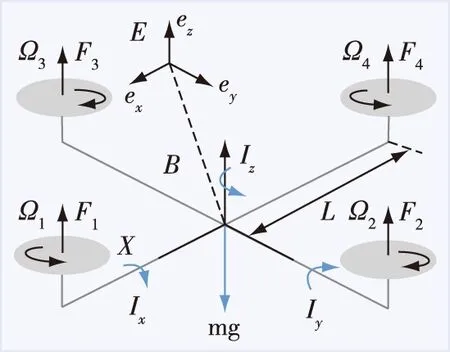
其中,x是状态向量,β是一个大于0的常数,q,p是满足q 此外,对于三维空间中高度非线性、强耦合和时变的AUV系统,单靠系统本身难以处理未知参数和不确定扰动,而后退法是一种简便有效的控制器设计方法,也是根据李雅普诺夫稳定性设计控制器的有力工具.因此,近年来,不少学者尝试将后退技术与SMC相结合,并应用于水下机器人的三维运动控制与协同[36-37].2019年,Bian等[38]给出了一种结合SMC、后退技术、领航-跟随策略的三维协调控制方案,所设计的新型控制律能够有效保证AUV在三维水下空间中轨迹跟踪的稳定性. 表1 典型滑模面设计的总结 虽然上述基于SMC的编队控制策略具有不错的控制效果,但以下几个方面值得注意:一方面,无论是线性滑模还是终端滑模、积分滑模等非线性滑模,它们还是存在一定的抖振效应,这无疑降低了多机器人系统的鲁棒性;另一方面,诸如AUV水下机器人通常在非常复杂的环境中工作,很容易受到未知的力量影响,包括海浪、潮汐、洋流以及向上或向下的水流等,这些不确定因素会造成高度耦合性、时变性、参数不确定性,极大地限制了多机器人编队控制在实际中的应用.因此,在上述研究的基础上有必要开发出一种适用于复杂实际环境下的多机器人编队控制器,并对模型动力学和可能存在的不确定性进行研究. 虽然SMC具有响应快、自适应和鲁棒性较强的优点,也能够满足机器人的非线性鲁棒控制,但多机器人系统是一类高度非线性、强耦合、时变性的复杂系统,在基于运动学或动力学模型实施一般的滑模变结构控制时,还存在以下缺陷: 1)SMC本身控制律的不连续性容易引起抖振现象,从而造成系统的不稳定; 2)SMC在实际应用中容易受到测量噪声等干扰; 3)对于非线性多机器人系统的滑模控制,等效控制的计算需要精确的数学模型,这就增加了SMC对系统模型的依赖性. 以上问题都降低了SMC的控制性能,因此,SMC存在的不足促使其与其他控制方法相结合.相对于一般滑模而言,这样的结合以及改进使得系统在保持对摄动和外部干扰具备更强鲁棒性的同时,尽量消除抖振现象的发生. 目前,智能控制与SMC的交叉研究已取得了一定的实际成果和应用,这对于解决复杂非线性、不确定性的多机器人编队控制问题具有十分重要的意义.当然,各类智能控制方法也都存在各自的长短处,需要针对具体控制问题进行具体研究分析.比如,模糊控制不仅不需要建立精确的数学模型,还能将不连续的控制信号进行平滑处理,从而抑制滑模变结构控制中所固有的抖振现象,但是模糊控制本身的设计缺乏系统性,其模糊规则的选择多采用试凑法,这对复杂控制难以奏效;同样,神经网络控制一方面具有较强的自学习能力,可以充分逼近任意复杂的非线性,但另一方面,其学习速度较慢,不易判别稳定性.因此,在面对复杂的多机器人编队控制问题时,需要以上各种控制方法的结合与补充,这样才能达到理想的无抖振滑模控制效果.表2对比了3种常见的智能控制方法. 神经网络具有较强的学习能力和较高的并行计算能力,且能够逼近任意复杂的非线性关系.虽然SMC具有简单、快速和鲁棒性等优点,但在非线性系统中仍存在一些重要的局限性,比如抖振现象、对不匹配不确定性的敏感性和选择最优不连续增益等[39-40].其中,抖振现象被认为是最显著的问题,利用神经网络能够有效抑制SMC固有的抖振问题.从20世纪末开始,许多专家将目光投向于SMC与神经网络结合的研究工作. 表2 3种常见的智能控制方法 3.1.1 常规神经网络滑模编队控制 神经网络在SMC中的应用主要分为两大类:一类是利用神经网络调整SMC的系统参数,实现SMC参数的自适应;另一类是将神经网络运用到SMC中,用来处理系统中的不确定性因素,计算等效控制. 第1类.SMC的抖振大小是由其控制器切换项的增益决定的,采用神经网络可对切换项的增益进行优化调节,能够在保持SMC强鲁棒性的前提下降低SMC的抖振.2012年,Gao等[41]就通过梯度下降法调整神经网络的权值,以此实现RBF神经网络优化滑模控制器的切换增益,从而有效抑制了抖振现象.但由于目前大多数神经网络都是基于梯度下降法的,因而对于非凸的优问题,它往往容易陷入局部最小点.为进一步提高神经网络的全局优化效率,2016年,Zhao等[42]提出了一种基于遗传算法优化的神经网络自适应滑模控制策略,通过遗传优化算法解决了隐藏层神经元节点数和各参数取值的问题,提升了滑模控制器的性能. 第2类.目前用于函数逼近的神经网络主要包括RBF和BP(Back Propagation)网络,其中RBF网络的学习速度和逼近精度都比BP网络强大,能够估计不确定性的上界,并对未知参数和非参数扰动进行补偿,因此RBF网络在处理多机器人编队参数不确定问题中的应用更为广泛.文献[43-45]涉及了多种不确定性环境下AUV编队控制的策略,但从收敛时间来看,这些控制策略并不理想.2019年,Cui等[46]提出一种基于非奇异快速末端滑模和RBF网络的新型控制器,它利用RBF神经网络技术对海洋恶劣环境引起的不确定性动力学和力进行近似分析,与传统控制策略相比,该控制方案具有更强的鲁棒性,并已成功应用于多AUV编队的轨迹跟踪. 3.1.2 深度神经网络滑模编队控制 到目前为止,人们提出了RBF、BP等多种神经网络模型,虽然这些神经网络能够提升SMC的控制性能,但其本身也存在一定的缺陷,特别是随着神经网络层数的加深,优化函数越来越容易陷入局部最优解;同时,随着网络层数增加,“梯度消失”现象更加严重.基于此,Hinton等[47]在2006年提出利用预训练方法缓解局部最优解的问题,将隐含层推动到了7层,神经网络真正意义上才有了“深度”,由此也揭开了深度学习、强化学习等先进学习算法的热潮. 深度学习(Deep Learning)和强化学习(Reinforcement Learning)虽是两种学习算法,但深度学习可以用到强化学习上,并称为深度强化学习(DRL).DRL将深度学习的感知能力和强化学习的决策能力相结合,可以直接根据输入的信息进行控制,是一种更接近人类思维方式的人工智能方法.目前,DRL算法已被应用于多个领域,例如多机器人控制技术:创建能够进行“学会学习”的智能体(agent),这种agent能够泛化处理以前从未面临过的复杂控制环境.同时,引入DRL算法能够为解决SMC固有的抖振问题提供新思路.文献[48]提出了一种基于强化学习策略的自适应积分滑模控制器,该控制器在较低抖振时能够获得奖励,在较高抖振时得到惩罚,以此减小了滑模切换引起的抖振效应. 需要指出的是,虽然DRL与SMC在编队控制领域的结合研究还处于起步和理论阶段,但近年来取得了一些突破,可以预见的是未来其发展具有很大的潜力.2018年,Sangiovanni等[49]提出了一种DRL算法与SMC结合的新型机器人运动控制方案,该方案结合经典的SMC概念和AI元素,为解决复杂的多机器人协同控制提供了一个新颖思路.上述文献所提方案具有集中式和分散式两种控制结构,其一方面利用积分滑模(Integral Sliding Mode,ISM)控制器对由于未建模的动力学或耦合效应而产生的匹配扰动和不确定项进行补偿.基于ISM控制的滑模面和控制律方程如下所示: (11) uISMj(t)=-Kjsgn(Σj(t)), (12) 其中,σj代表实际滑动变量,uj代表控制器的输入量,m是一个正常数,e2j代表误差参数,sgn()是符号函数,Σj(t)代表辅助滑动变量.另一方面,他们设计了一个基于DRL的决策机制,其工作原理是利用DRL算法训练神经网络,根据机器人性能的要求,选择适当的奖励函数,以选择两种控制结构中一个最优的解决方案.其中,奖励函数(切换规则)如下所示: (13) DRL和SMC在机器人碰撞避免策略方面具有很大的潜力,但在以往的研究中,往往只考虑了碰撞因素,而未将其进一步拓展到编队控制领域.基于这一问题,2019年,Sui等[50]提出了一个学习行为策略的两阶段训练方案,并设计了一个评估状态值的价值网络.其学习任务主要分为两个阶段,具体来说,第一阶段采用模仿学习方法,提出基于共识和最优交互避碰的引导方法,生成初始化行为策略的演示轨迹;第二阶段采用强化学习方法,细化策略,在设计RL中的奖励函数时,综合考虑到了编队因素和碰撞因素.此外,该方法还采用LSTM神经网络去感知环境中任意数量障碍物的信息,网络框架如图5所示. 图5 LSTM神经网络的模型[50]Fig.5 Model of LSTM neural network[50] 如图6所示,绿色的方块代表follower的状态,蓝色的方块代表leader的状态,红色长方体表示处理障碍物状态的LSTM模块.而红色的立方体是LSTM的最后一个隐藏状态,它表示障碍物的编码信息,并将跟随者、领导者和障碍物的状态合并起来,然后送入3个全连接(FC)层.最后,网络输出当前状态的估计值. 图6 系统网络的结构[50]Fig.6 Network architecture to deal with formation control[50] 在对多机器人进行编队控制时,还应考虑到自然物力的影响,例如AUV的运动速度对水中阻力和升力系数的变化十分敏感,在不同速度下固定SMC参数又很难实现对AUV的精确运动控制,如果参数完全依赖于手动调整,那么工作将是繁琐的,也不能保证良好的鲁棒性.目前,主流的参数整定方法有模糊逻辑法[51]、基于神经网络法[52]、进化算法[53],其中模糊逻辑对先验知识要求较多,存在参数优化问题;基于神经网络的方法,一般采用监督学习来优化参数,而在监督学习中指导信号难以获取;进化算法对先验知识的计算要求较少,但计算时间较长,难以实时控制.而强化学习在自适应控制领域中发挥着重要作用,它能够在外部环境没有提供清晰训练信号的情况下,通过系统与环境的相互作用有效地学习控制策略. 针对上述问题,2019年,Wang等[17]采用一种基于深度确定性策略梯度(DDPG)的滑模控制算法,实现了不同速度下AUV的协同编队控制.深度确定性策略梯度算法是由Lillicrap等[54]利用深度Q网络(DQN)扩展Q学习算法的思路对确定性策略梯度(DPG)方法进行改造,所提出的一种基于Actor-Critic框架的算法,可适用于传统DQN算法解决不了的连续动作空间上的DRL问题.该方案中DDPG包含两个神经网络,一个是在当前时间步长的情况下,引入一个批评家神经网络来评估所设计控制的长时间性能,另一个是在相应状态下输出连续动作的动作神经网络.同时,为提高学习效率、防止局部最优,创建了一个样本库存储历史样本,每次随机选择一定数量的样本进行再训练.这种基于无模型强化学习算法的控制策略,不仅保证了AUV编队在不同速度下的协同控制,并且其稳定性、收敛性和精确度都得到了提升.DDPG滑模控制策略的结构如图7所示. 图7 基于DDPG滑模控制法的结构[17]Fig.7 Structure based on DDPG sliding mode control method[17] 文献[17]所提出基于DDPG的滑模控制方法,虽然在仿真结果中验证了该方法在水下航行器航向控制中的抗干扰性和跟踪能力,然而,该方法的收敛速度受到诸多因素的影响,其实际应用还没有得到充分的验证.在今后的工作中,需要进一步提高该方法的收敛速度和稳定性,使其能够应用于水下航行器的实际航行实验控制中. (14) 其中,s,a分别代表智能体的状态和动作,μ是贪婪策略函数,P(s|θp)是一个与状态相关的正定方阵.与以往的避障算法相比,该方案是一种无模型方法,因此可大大减少建模和实现阶段的时间.表3为几种典型深度强化学习算法的总结. 模糊逻辑控制(Fuzzy Logic Control,FLC)的基本思想是把专家对特定控制对象过程的控制策略总结为“IF,THEN”式表达的控制规则,通过模糊推理得到的控制作用集,作用于被控对象或过程. 传统控制方法一般是基于模型的控制,而多机器人系统相对于其他被控系统难以用精确数学模型来描述.与其他基于模型的方法不同,FLC的设计主要依赖于专家的知识和经验,对系统模型没有依赖性,因此,对于具有不确定性的非线性系统,FLC是一种有效的控制策略.此外,FLC能够保持SMC在滑动模态阶段对参数不确定以及信号扰动的鲁棒性,利用FLC的输出代替SMC中的符号项,能够对控制信号进行平滑处理,从而有效削弱抖振. FLC与SMC结合的原理主要分为两方面:一方面是滑模控制器为主控制器,模糊系统起辅助作用[57-58];另一方面就是模糊系统直接用于设计滑模[59-60].同时,FLC与SMC结合的应用方式通常有:常规模糊滑模控制、自适应模糊滑模控制、基于模糊神经网络的滑模控制、基于优化算法的模糊滑模控制等. 无人机(Unmanned Aerial Vehicle,UAV)因具有能够在各个方向移动、低速盘旋、垂直起飞和降落等特点,已广泛应用于目标侦察、支援救灾、机动巡逻、农业植保等领域.对于无人机的编队控制,通常还需要考虑实际环境中负载变化、参数摄动、测量噪声、传动系统的非线性及外部扰动等不确定性因素的影响.许多研究结果表明,将SMC和FLC技术相结合应用于UAV等多机器人编队控制中,不仅可以减轻SMC本身抖振效应、减少模糊规则数量,还能保证UAV编队系统对外界不确定因素的抗干扰能力. 在FSMC(模糊滑模控制)控制器设计时,趋近律设计是一个重要的组成部分.其中,幂趋近律是应用最多的趋近律之一,与其他趋近律相比,其优点是当系统处于接近滑动面的状态时,趋近速度会逐渐减小,这就使得幂趋近律具有较好的消弱抖振的性能,但缺点是当系统状态远离滑动面时,到达速度较慢.针对这一问题,Xi等[61]提出了一种基于模糊趋近律的滑模控制策略,设计了兼顾抖振抑制和位置跟踪的模糊趋近律,该控制律对外部扰动不敏感,既能有效地控制抖振,又能实现UAV的快速跟踪.如图8所示,FSMC的设计步骤一般可分为模糊化、建立知识库、去模糊化三步(在模糊滑模控制中输入不再是跟踪误差e,而是滑模函数s). 此外,Xi等[61]还给出了模糊规则和模糊关系,如表4所示. 表3 DRL经典算法的总结 图8 FSMC的结构[61]Fig.8 Architecture of FSMC controller[61] 表4 模糊关系表[61] 表4中,PS、ZR、PM、PB分别是对模糊控制输入|s|和输出k的语言值定义即负小(positive small)、零(zero)、正中(positive medium)、正大(positive big).相应的模糊关系(A,B分别是|s|和k的模糊子集): Ri:if|s|isAi,thenkisBi,并进一步得到模糊控制的趋近律: (15) (16) 从式(16)可看出趋近律满足滑模趋近条件,说明该模糊滑模控制满足稳定性要求. 目前,常规FSMC的设计仍然是基于经验的,系统参数在控制过程中没有自适应和自学习能力,而且在很多情况下有效经验的获取并不容易.基于此,2019年,Eltayeb等[62]提出了一种自适应模糊增益调度的滑模控制器(Adaptive Fuzzy Sliding Mode Control,AFSMC),除了能够和常规FSMC一样对跟踪误差和不确定性部分进行补偿,其特色还在于切换增益比常规FSMC要小很多,有效地减少传统SMC的抖振,并可用于四旋翼无人机的轨迹跟踪. FNN(模糊神经网络)由于结合了模糊控制与神经网络控制两者的优势,不仅具有神经网络自学习和快速并行处理的能力,而且具有模糊控制系统能够充分利用先验知识、以较少的规则数来表达知识的优势.近些年,很多学者将FNN-SMC研究工作的重心放在了控制器的简化上.2017年,Zeghlache等[63]提出了一种基于区间型模糊神经网络控制器的滑模控制方法,该控制方案避免了建模困难,不仅减小了SMC的抖振效应和FLC控制器的规则数,还有效保证了UAV编队的稳定性.2019年,Ferdaus等[64]在文献[63]的基础上,利用FNN系统以较少的学习参数来发展一个精简控制器(Reduced Parsimonious Controller,RedPAC),这种RedPAC智能控制器与传统FLC或基于FNN的智能控制器不同,它没有前提参数,因此大大减少了参数的数量,从而消除了控制器设计过程中的繁琐问题,并利用SMC技术来适应RedPAC的后向参数,基于SMC的辅助补偿控制项能够保证四旋翼UAV跟踪误差的一致渐近收敛为零. 对于典型非线性的多机器人控制系统,模糊滑模控制器的设计在本质上可视为一个多参数的优化问题,同时,很多研究证明了遗传算法(Genetic Algorithm,GA)是自动化模糊控制规则库和成员函数定义的强大工具,可以利用GA来寻找控制器的最优规则和隶属函数.在过去的数年里,GA的优点也扩展到了设计模糊滑模控制器的各种方法.Babaei等[65]提出了基于遗传算法的模糊滑模控制方法,采用GA算法以优化输入输出比例因子等参数以获取更好的控制效果,提升了常规模糊滑模控制器对不确定性和外部干扰的鲁棒性,并应用于不确定、非线性的UAV系统.利用遗传算法还能够有效抑制SMC固有的抖振现象,2019年,Vahidi-Moghaddam等[66]针对多输入多输出、不确定非线性的UAV系统,在文献[65]的基础上设计了基于干扰观测器的模糊终端滑模控制器,利用GA优化的观测器保证了干扰估计误差在有限时间内收敛指至零,并有效抑制了抖振效应. 多机器人系统是一个存在不确定性的复杂系统,针对不确定性问题常有两种控制策略.一是自适应控制,通过对控制规律的及时识别、学习和调整,可以达到一定理想的控制性能指标.然而,在20世纪80年代,研究人员发现,当控制系统的参数发生变化或存在外部干扰时,传统的自适应控制难以保证系统的稳定性.二是鲁棒控制,它可以在不确定因素的一定变化范围内,保证系统稳定和维持一定的性能指标,是一种固定控制,易于实现.因此,鲁棒控制与自适应控制的结合可以取长补短. 鲁棒自适应控制即鲁棒控制与自适应控制的结合,是一种具有很好控制系统性能的智能控制方法,其中鲁棒项可对系统外部干扰进行抑制,自适应律可保证滑模切换增益实时调节.因此,将鲁棒自适应控制与滑模变结构控制相结合也就成为了一个研究热点[67]. 与固定翼飞机相比,四旋翼飞机由于体积较小,可垂直起飞、着陆、悬停,并能够在室内、室外等多种环境下飞行,因此,在军事、民用领域如多无人机作战、环境监测等方面具有巨大的潜力. 近年来,各种四旋翼飞行器姿态稳定控制研究得到了飞快发展.但四旋翼无人机在室外环境下进行编队飞行时,很容易遭受不可控的外部环境扰乱,会导致执行器发生故障,从而对UAV编队的稳定性造成挑战,而PID等控制策略并不能保证四旋翼无人机在飞行任务中遭受严重外部环境和执行器故障时的优良性能.因此,容错控制(FTC)成为了UAV姿态控制器设计的一个重要因素. 一般来说,容错控制分为被动容错控制(Passive Fault Tolerant Control,PFTC)和主动容错控制(Active Fault Tolerant Control,AFTC).以往的研究主要集中在PFTC,比如基于反馈线性化[68]、H∞的自适应控制方法[69]等,虽然这些方法对故障补偿有一定的效果,但在系统矩阵不准确的情况下,对扰动和不确定性的鲁棒性较差.为了克服这个问题,Gong等[70]提出一种基于积分滑模和鲁棒自适应技术的固定时间容错控制器,该控制器的切换控制结构限制了系统的抖振现象,并通过ISM解决了四旋翼无人机容错姿态的稳定控制问题.2019年,Nguyen等[71]提出了一种改进的自适应滑模反步控制方案(MASBC).如图9所示,首先通过一个故障诊断单元来估计执行器故障的大小,并在此基础上将故障估计与自适应滑模反步控制相结合,设计了MASBC控制器来适应执行器故障,克服了执行器的饱和限制和干扰.与以往方法相比,该方案还具有更好的跟踪性能和更快的补偿速度. 图9 基于MASBC的控制结构[71]Fig.9 Control structure based on MASBC [71] 文献[71]还给出了四旋翼无人机的动力学方程,如图10所示,它建立在惯性坐标系B和地球坐标系E中. 图10 四旋翼无人机的受力矩[71]Fig.10 Torque of quadrotor [71] 此外,四旋翼无人机的控制器参数是根据恒载和外部干扰因素进行调整的.然而,无论是在军事领域还是民用领域,四旋翼都会遇到各种负载情况,如投掷武器、快递等,变负载作为一个大的内部扰动因素,导致控制不稳定.为此,Liu等[72]于2019年提出了一种新型的鲁棒滑模控制器设计方法,在控制抖振的同时,在变负载条件下对期望轨迹进行实时跟踪.该控制器由基于学习率的滑模曲面和基于滑模反双曲函数的滑模趋近律组成,将z轴方向方程作为动力学方程,代入滑模面得到控制输入,所提出基于学习速率的滑模曲面设计如下: (17) (18) 还有一点需要注意的是,多机器人编队中各个机器人的通信依赖于网络,所以在实际控制中还需要考虑到网络引起的时延、数据包丢失和数据包无序等通信约束.针对这一问题,Li等[73]提出了一种基于观测器和二阶离散自适应滑模函数的鲁棒自适应滑模控制方法,它不仅实现了滑动运动的可达性,还结合网络预测控制法实现了对通信约束的补偿. 总之,虽然鲁棒自适应滑模控制可对系统外部干扰进行抑制并消除抖振问题,但实际上想要同时兼顾自适应和鲁棒性的最优控制比较困难,这些问题还有待解决. 本文阐述了滑模变结构控制的原理、发展起源以及存在的问题,然后将滑模变结构控制与神经网络控制、鲁棒自适应控制、模糊控制等先进智能控制方法相结合,分析了这些常规滑模控制与智能滑模控制策略在多机器人协同控制中的应用现状,并对以上各种方法进行了总结. 根据对已有研究成果的论述分析,下面对该研究领域的未来进行展望.多机器人协同控制系统是一门集计算机信息、通信技术、自动控制以及人工智能的复杂学科,代表了当今科技领域的前沿,对多机器人协同控制的研究是潮流所趋,其价值已得到学界的广泛认同.同时,基于SMC的多机器人协同编队控制研究,虽然已取得不少成果,但在复杂的实际工程应用中,仍存在以下几方面的问题有待探索: 首先,在网络化多机器人集群编队控制中,其后期的主要问题是网络问题,携带多种传感器、控制器、执行器的agent之间的信息交互主要依赖于良好的通信网络,以此构成一个反馈控制系统.然而,在实际中网络由于自身原因以及受到外界环境的干扰,存在通信延迟、数据丢包、数据包混乱等问题,因此,采用连续时间滑模控制的方法不切实际,而离散时间滑模控制(Discrete Time Sliding Mode Control,DSMC)控制与连续时间滑模控制系统不同,DSMC具有不变性,能够对不稳定的通信信号进行优化.目前,关于SMC在离散时间系统的研究相对较少,所以基于DSM的多机器人协同编队研究仍有很大潜力待挖掘. 其次,人工智能与控制学科的交叉本就是一个艰巨的任务,人工智能相关算法的更新迭代速度很快,基于神经网络滑模控制等智能滑模编队控制的算法在收敛性和稳定性方面仍有提高空间,特别是DRL与SMC的结合在解决典型非线性多机器人协同控制问题上具有良好的效果,但相关研究仍处于起步阶段.因此,如何更合适地利用深度神经网络与滑模变结构控制,也是多机器人协同编队控制领域未来的研究热点和重点突破方向. 此外,伴随社会和科技的发展,将来必然会出现集群规模更庞大,人机共融的异构多机器人协同进行作业,来完成更加复杂的任务.其中,共融机器人是未来机器人发展的必然趋势,也是“中国制造2025”计划的核心.共融机器人是指能与作业环境、人和其他机器人自然交互、自主适应复杂动态环境并协同作业的机器人.要实现大规模、异构多机器人的共融,这对于控制系统的性能要求更高,对于从事SMC和多机器人控制等相关研究的学者来说,也是一个巨大的挑战.正因如此,我们才需要进一步探索能够满足大规模、智能化、多类型异构的机器人群体协同控制策略.
3 基于智能SMC的编队控制
3.1 基于神经滑模控制的多机器人编队
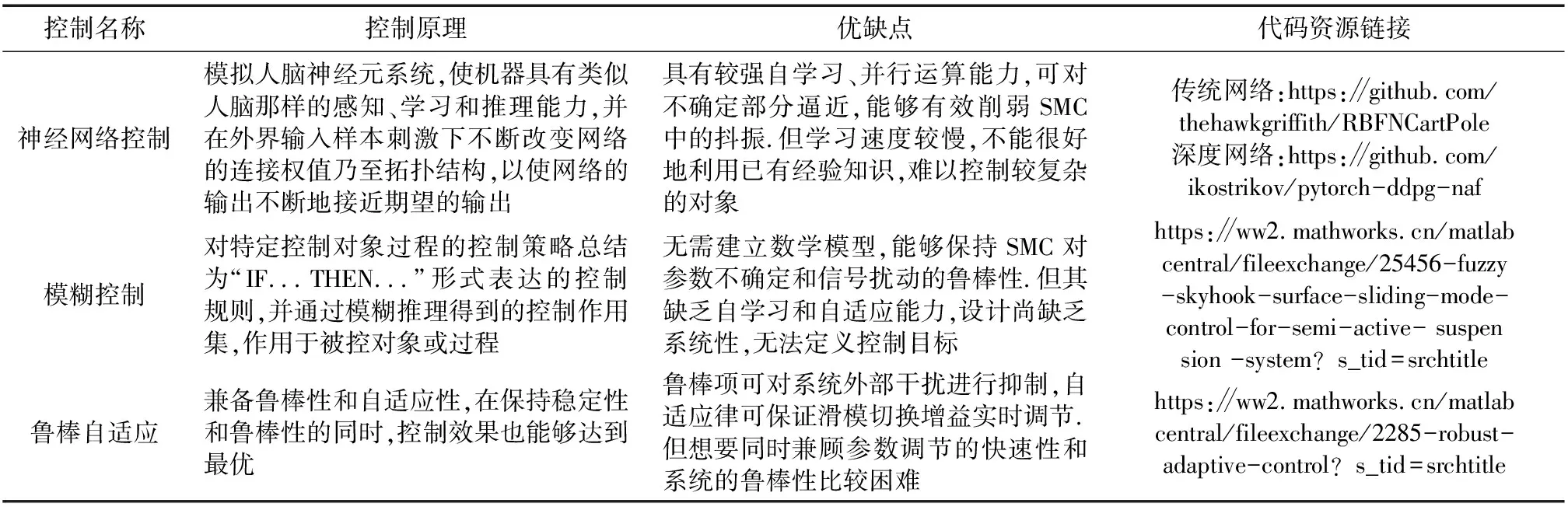
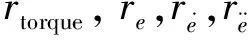
3.2 基于模糊滑模控制的多机器人编队



3.3 基于鲁棒自适应滑模控制的多机器人编队
4 结论与展望
