多波束卫星通信系统波束干扰下的资源分配策略研究
2022-05-18司闯李鹏史传胜葛旗伟
司闯 李鹏 史传胜 葛旗伟
0 引言
基于卫星的物联网系统正受到各个领域研究人员的密切关注,但物联网多连接、低功耗的特点给传统的卫星通信系统带来了巨大的挑战[1].万物互联通信将会是未来物联网时代的重要组成部分[2-3].利用资源分配技术,多波束卫星系统可以满足物联网日益增长的通信业务需求.然而在多波束卫星通信系统中,星上资源非常有限,当面对海量的通信业务请求时,功率带宽等资源便显得尤为珍贵.如何合理有效地分配星上资源,从而最大化地满足业务需求,成为卫星通信领域研究的热点.
针对多波束卫星通信系统中资源分配的问题,文献[4]提出两种资源优化模型,一种是在功率和频谱分配中寻求折中,另一种采用优化带宽来提高传输速率;文献[5]提出一种低轨卫星的多波束资源联合分配方案,但没有考虑业务时延的问题;文献[6]提出一种不考虑波束间干扰的下行链路功率分配模型;文献[7]建立了基于卫星链路的容量计算模型来对功率进行优化.其中,文献[5-7]仅是优化功率,没有考虑到带宽的灵活分配,对带宽资源造成了一定的浪费.文献[8]构建了一种资源分配模型对功率和频带做联合优化;文献[9]和文献[10]在基于点波束干扰的前提下,分别提出一种功率和带宽联合分配算法,把最小化业务需求量与所分配容量差值平方数作为优化目标,但均未考虑存在时延的实际情况.在多波束卫星系统中,点波束之间的干扰问题不可忽视,文献[11]研究了多波束卫星系统上行与下行链路中的同频波束干扰.
由于星地距离较远,信号传输会有时延的情况存在,并且卫星传输过程中产生的干扰功率会影响地面网络的通信质量.因此,对于存在点波束间干扰和有时延限制的多波束卫星通信系统,本文提出一种以二阶业务未服务量[7]作为优化目标函数的功率带宽联合优化算法,约束了卫星的最大传输时延和干扰功率,优化系统容量,逼近业务需求量,并且利用拉格朗日对偶理论和次梯度下降法获得了此算法的最优解.
1 系统模型
多波束卫星通信系统如图1所示.该系统由对地静止地球轨道卫星、多个点波束以及多个卫星用户组成,系统返向业务信道采用频分多址(Frequency Division Multiple Access,FDMA)体制.由于卫星用户有实时业务需求,所以相关点波束的业务需求是高度动态的.假设此系统中多波束卫星共有N个波束,第i个点波束覆盖的系统容量为Ci,用户业务需求量表示为Ti;系统的总功率资源为Ptotal,分配给第i个点波束的功率为Pi;系统的总带宽资源为Wtotal,分配给第i个点波束的带宽为Wi.

图1 多波束卫星通信系统Fig.1 Multi-beam satellite communication system
利用多波束天线和频率复用方案,卫星系统可以在同频信道中同时发送多个信号,但在这种情况下,使用相同频率的点波束之间会产生干扰,如图2所示.为了表示系统的波束间干扰,引入波束间干扰矩阵H:
(1)

(2)
其中,N0是每个点波束的噪声功率谱密度.从式(2)中可以得出,第i个点波束的容量Ci的大小和分配给此点波束的功率Pi以及带宽Wi成正比.然而由于存在波束间干扰,Ci会随着分配给其他点波束的功率增加而减少.所以,每个点波束的容量的大小不仅仅取决于分配给它的功率以及带宽,还取决于分配给其他点波束的功率和带宽.

图2 卫星下行链路的同频干扰Fig.2 Co-channel interference in satellite downlink
2 功率带宽联合分配算法
在多波束卫星通信系统中,不同用户的通信业务需求也不同.其中语音、视频等实时业务有严格的时延要求.若用Ai表示产生新的业务需求增长速率,Ui表示由于通信业务完成导致的业务需求下降速率,为了保证系统的通信服务保持稳定,系统需要满足下列条件:
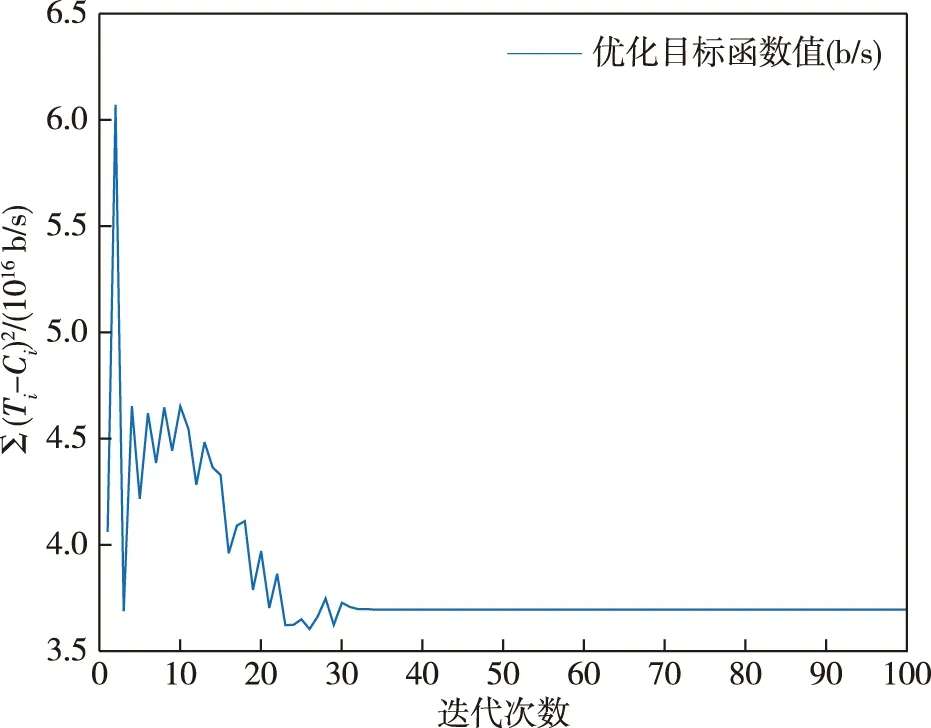
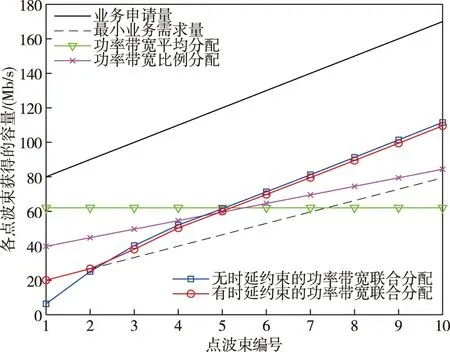
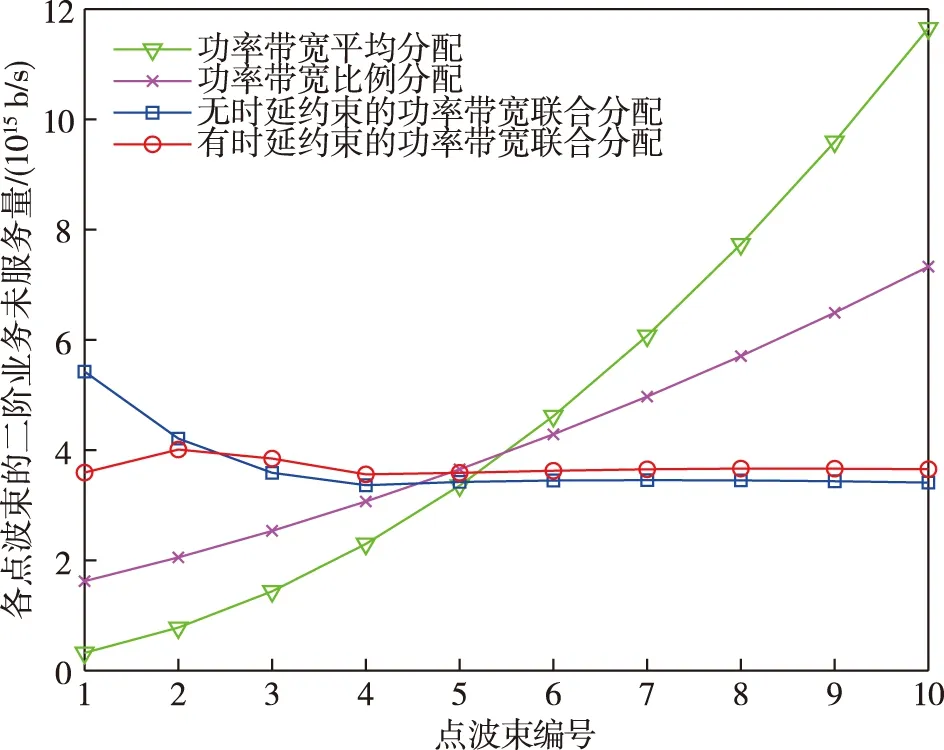
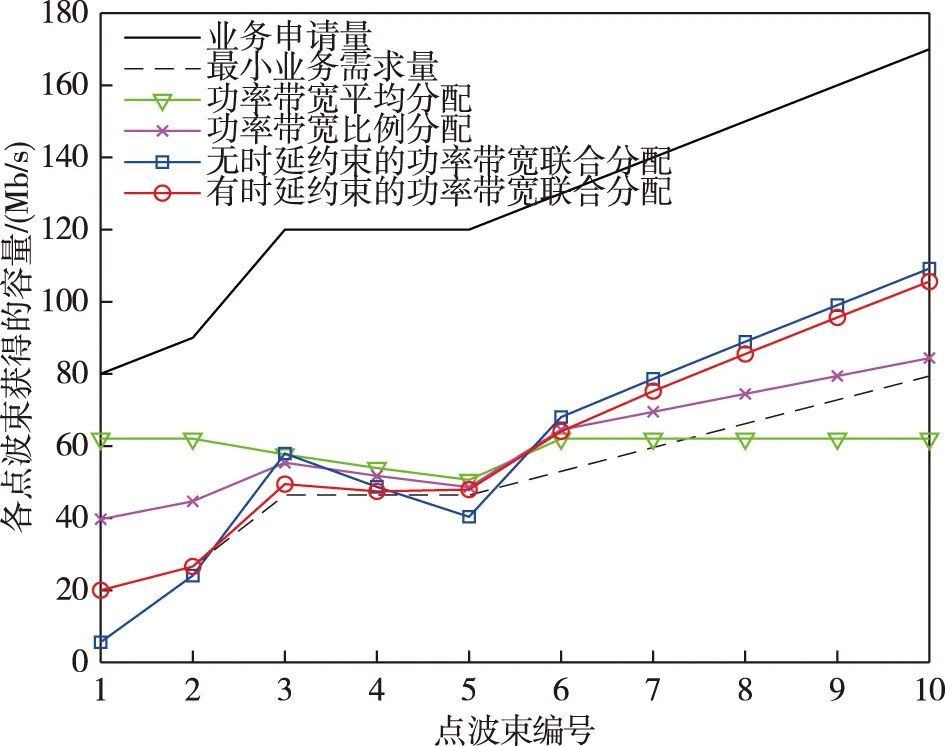
Ti<∞,Ai (3) 第i个点波束在系统稳定状态下的时延di[12]可以表示为 (4) 其中,ei是第i个点波束下行链路的误包率,ei<1.对于有严格时延限制的通信服务,用Di表示第i个点波束的最大时延限制,所以系统的时延di应该满足条件: di≤Di. (5) 与式(4)结合,可以得到: (6) 即: (7) 其中,(1-ei)Di>1.根据式(7),可以将时延约束转化为最小业务需求量的约束,即每个点波束的最大时延限制决定它的最小业务需求. 为了评估分配算法的性能,选择合理的评判指标至关重要.本文的最终优化目标是点波束所分配到的容量最大程度接近它们的业务需求.基于以上约束条件,本文采用二阶差分函数作为优化目标来最小化它们的差距[9].为了量化业务需求与实际所分配的系统容量之间的差距,将二阶业务未服务量函数定义为(Ti-Ci)2,其中Ti是第i个点波束的业务需求量,Ci是分配给i个点波束的容量. 假设本文多波束卫星系统有N个点波束,为了最大化满足每个点波束的通信需求,分配给点波束的容量应与它的业务需求量接近,因此可以根据上述条件建立如下数学模型[13-14]: (8) s.t.Ci≤Ti, (9) (10) (11) (12) (13) 其中,i∈(1,2,…,N).式(9)表明点波束的容量不能大于它的业务需求量,避免造成资源浪费;式(10)表明分配容量的下限与时延有关,每个点波束都受到最小业务需求的限制;式(11)和(12)分别表明分配给每个点波束的功率之和与带宽之和不能大于系统的总功率与带宽资源;式(13)中,Pint是保证地面间网络通信服务质量的最大干扰功率,gi是第i个点波束的信道增益,此约束可以确保卫星通信产生的干扰不会影响地面网络通信的服务质量. 当各点波束相互之间不存在干扰时,点波束干扰矩阵中的每个元素都为0,上述问题便是凸优化问题.但此资源分配模型中考虑了点波束间的相互干扰,优化变量Pi是相互耦合的,此优化问题不属于凸优化问题,因此可以从对偶问题的角度来获得联合优化问题的最优解. 引入非负对偶变量ρ,λ,μ和ν,可以得到联合优化问题的拉格朗日函数为 L(P,W,ρ,λ,μ,ν)= (14) 其中,ρ=(ρ1,ρ2,…,ρN),P=(P1,P2,…,PN),W=(W1,W2,…,WN). 从式(9)可以得到拉格朗日对偶函数为 f(P*,W*)=d*, (15) 其中,d*是原问题约束条件下的最优解,可以通过拉格朗日对偶理论和次梯度下降法获得. 具体说明,原优化问题可以分解为以下3个子问题: (16) (17) 其中 E= (18) 3)子问题3(更新对偶变量):利用次梯度下降法对对偶变量进行迭代更新: (19) 其中,[x]+=max{0,x},n是迭代次数,Δn是迭代步长.只要Δn的值选择适当,则次梯度下降法可以保证对偶变量快速收敛到最优解. 本文提出的算法步骤具体描述如下: 步骤1.为对偶变量ρ,λ,μ,ν和迭代精度ε设定适当的初始值,设定最大迭代次数n.令每个点波束的初始带宽Wi=Wtotal/N,i∈(1,2,…,N). 步骤6.资源优化分配完成. 根据上述过程,如果步骤2中计算单个点波束分配功率的数值方法复杂度为O(S),则步骤2、步骤3和步骤4的计算复杂度分别为O(SN)、O(SN)和O(2+N),其中N是点波束的个数.因此,该算法的总计算复杂度为O(2KSN+2K+KN),其中K为迭代次数.此算法的复杂度与点波束的数目成线性关系,表明该算法在实际应用中具有可行性. 算法流程如图3所示. 图3 资源优化分配算法流程Fig.3 Flow chart of the optimized resource allocation algorithm 在本文多波束卫星通信系统模型中,共有10个点波束.系统总功率资源为200 W,总带宽资源为500 MHz,每个点波束的噪声功率谱密度N0为0.2×10-6W/Hz.根据文献[4],点波束干扰矩阵中元素的值设为 (15) 通过仿真对比以下4种算法,验证本文所提出算法的性能: 1)本文提出的考虑时延约束的功率带宽联合分配算法,时延约束可转换为最小业务需求量约束,如式(6)和(7)所示. 2) 不考虑时延约束的功率带宽联合分配算法[9]. 3) 功率带宽平均分配算法[7]:Pi=Ptotal/N,Wi=Wtotal/N. 4)功率带宽比例分配算法[16]:Pi=PtotalTi/Ttotal,Wi=WtotalTi/Ttotal. 所有点波束的信道条件相同时,假设每个点波束的业务需求量以步长10 Mb/s从80 Mb/s递增到170 Mb/s,最大迭代次数n=100.目标函数迭代过程数值变化如图4所示,经过有限次数的迭代,优化目标函数值收敛到了稳定值,收敛速度的快慢取决于对偶因子迭代步长的大小. 图4 总二阶业务未服务量的收敛情况Fig.4 Convergence of unserved quantity of total second-order service 图5为4种算法分配容量的仿真结果.由图5可以看出:平均分配算法[7]将功率带宽平均分给每个点波束,业务需求量较小以及业务需求量较大的点波束的容量大小相同,导致资源浪费;比例分配算法[16]按照业务需求量的比例进行资源分配,无法满足每个点波束的最小业务需求,系统总容量较低;无时延约束的联合分配算法[9]给点波束3~10分配的容量较高,但分配给点波束1的容量极低,不具有公平性,且系统总容量不能达到最优;本文提出的联合分配算法可以满足每一个点波束的最小业务需求,给业务需求量较高的点波束分配较多的容量,并且得到的系统总容量较其他3种算法更大,提高了资源利用率.4种分配算法的系统总容量如表1所示. 图5 相同信道条件下各点波束获得的容量Fig.5 Capacity of each spot beam under the same channel 表1 4种算法分别得到的系统总容量 信道条件相同情况下4种分配算法得到的二阶业务未服务量如图6所示:平均分配算法分配给每个点波束的资源相同,因此二阶业务未服务量与业务需求量成正比增长;比例分配算法在点波束1~4得到的二阶业务未服务量较低,但随着业务需求量的增长仍呈现上升趋势;无时延约束的联合分配算法在点波束1产生的二阶业务未服务量最大,不具有公平性;利用本文提出的联合分配算法业务需求量较高的点波束可以得到较低的二阶业务未服务量,从表2中可以得到,此算法最终得到的总二阶业务未服务量最小,即优化目标函数能够达到最优,体现了本算法的公平性与有效性. 图6 相同信道条件下各点波束的二阶业务未服务量Fig.6 Unserved quantity of second-order service for each spot beam under the same channel 表2 4种算法分别得到的总二阶业务未服务量 在信道条件不同的情况下,对信道条件不同的点波束设定相同的业务需求来分析4种分配算法的性能.假设10个点波束的噪声功率谱密度分别为0.2、0.2、0.25、0.3、0.35、0.2、0.2、0.2、0.2和0.2,业务需求量分别为80、90、120、120、120、130、140、150、160和170 Mb/s.4种算法的仿真结果如图7所示.平均分配算法给不同信道条件的点波束分配的资源较少,给业务需求量较低的点波束分配了较多的资源,造成资源浪费;比例分配算法同样给不同信道条件的点波束分配较少的资源;无时延约束的联合分配算法分配给点波束3的资源较多,分配给信道条件最差的点波束5的资源较少,且无法满足点波束1、2和5的最小业务需求;本文提出的分配算法对信道条件不同而最小业务需求量相同的点波束分配大小相近的资源,同时可以满足每个点波束的最小业务需求,但略微降低了点波束4和5的容量,把资源分配给业务需求量较大的点波束.在信道条件不同的情况下本文提出的算法仍然具有较好的公平性. 图7 不同噪声功率谱密度信道条件下各点波束获得的容量Fig.7 Capacity of each point beam under different noise power spectral density channels 图8是4种算法在不同信道条件下得到的二阶业务未服务量.从图8中可看出:平均分配算法和比例分配算法以及无时延约束的分配算法随着点波束3~5的信道条件变差,二阶业务未服务量都呈较快增长的趋势,无时延约束的算法在点波束5的二阶业务未服务量最大,以上3种算法的性能受到信道条件的影响较大;本文提出的算法在点波束3~5处的二阶业务未服务量的变化趋势较为平缓,受信道条件的影响较小,表现出较好的公平性. 图8 不同噪声功率谱密度信道条件下各点波束的二阶业务未服务量Fig.8 Unserved amount of second-order service for each spot beam under different noise power spectral density channels 卫星通信系统中的星上资源稀缺,为了提高星上资源的利用率,本文建立了多波束卫星系统下行链路的容量分配模型,考虑了点波束间的干扰、时延限制、对地面网络的功率干扰等条件,提出一种以二阶业务未服务量为优化目标的功率带宽联合分配算法,利用拉格朗日对偶和次梯度下降理论,将资源分配问题分为3个子问题,最终得到最佳资源分配方案.与已有的几种算法相比,本文提出的分配算法能够最大化减少业务需求与实际分配容量之间的差距,并且提高了系统容量;在信道条件不同的情况下仍能保持较好的公平性,具有更好的性能.
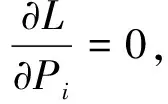
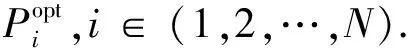
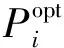
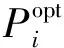
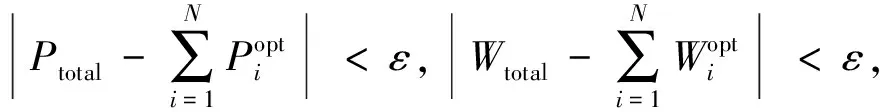

3 算法仿真与分析



4 结束语
