基于CNN-Attention-BP的降水发生预测研究

吴香华 华亚婕 官元红 王巍巍 刘端阳

0 引言

吉林省位于中国东北地区中部,大部分地区属于温带季风气候,降水、气温和气象灾害的时空分布差异较大．吉林省是我国重要的粮食和农产品生产地,稳定的农业生产环境是保证粮食产量的根本因素[1]．研究降水预测,对预防气象灾害、稳定农业生产和经济发展具有重要的战略意义[2]．

近年来,基于现代统计方法的人工智能理论和应用迅速发展,相关技术被广泛应用于降水预测中．运用现代统计模型和人工智能方法改进传统的降水发生模型,提高预测精度是科研和业务中提升管理水资源决策可靠性的迫切需求[3-4]．在运用Logistic模型对全国范围内强降水的研究中,引进主成分分析和Bootstrap抽样技术能进一步改善模型过拟合的问题[5]．将随机森林应用到降水发生的预测,并与C4.5决策树和SQIL决策树进行比较,发现随机森林的准确度高于其他类型的决策树,但建模所需时间远大于其他方法[6]．Ortiz-Garcia等[7]使用支持向量机(Support Vector Machine,SVM)预测降水量,与决策树、极限学习机等方法比较,并评估不同资料的可靠性,发现随着样本量的增加,SVM的核函数映射维度提高、计算量增加从而影响模型的时效性．

BP神经网络具有较好的非线性映射能力,比传统统计方法更加适合非线性的降水研究．在对不同环流型下的降水观测资料进行降尺度预报的研究中,发现BP神经网络对暴雨预测的相对偏差指数最小,预测效果最优[8]．在预报中心地区和周围地区运用多层感知机(Multilayer Perceptron,MLP)建立不同地区与降水之间的关系以预测3 h降水,比日本气象厅数值模式的均方根误差降低了1.5 mm[9]．针对较长时间尺度的历史数据,神经网络方法能够快速学习到数据的主要特征．李增[10]基于长达56年的东北地区气象观测数据进行干旱预测,结果发现,深度学习的神经网络模型比MLP的预测性能提高24.19%,且明显优于传统的统计预测模型．

卷积神经网络能快速捕捉降水数据的非线性关系并缓解过拟合问题,能够显著改善降水预报模型的效果[11]．当输入数据的向量维度过大,易出现维数灾难问题而降低模型的学习效率．Attention机制是一种有效获得良好结果的机制,其关键是对重要信息提高注意力,利用注意力机制确定气象因素对降水预测的影响权重．在卷积神经网络中加入Attention机制,通过对中间层神经元分配不同的概率权重,使得神经网络模型更加关注对降水发生影响较大的信息,减少甚至忽略对降水预测影响较小信息的关注[12]．

本文提出将Attention应用于卷积神经网络(Convolutional Neural Networks,CNN)中,加入BP神经网络(Back Propagation,BP)对整个组合模型进行调参．将预处理后的降水影响因素作为输入向量,进行神经网络降维．在 CNN隐藏层中,引入Attention机制来捕捉气压、风速、气温和相对湿度的特征对降水发生影响的重要程度．将经过CNN层和Attention层降维后的特征向量输入BP神经网络进行降水发生预测,并对模型性能进行评估分析．

1 研究数据与预处理

1.1 数据来源

本文的数据来源于国家气象科学数据中心(http:∥data.cma.cn)的中国地面气候资料日值数据集(V3.0)．根据不同的气候类型,选取吉林省的长春站、白城站、延吉站为研究站点,各站点信息见表1．选用1961—2020年夏季6—8月的20—次日20时本站平均气压(hPa)、平均风速(m/s)、平均气温(℃)和平均相对湿度(%)为物理协变量,降水发生与否为研究的目标变量．

1.2 数据预处理

对研究数据进行质量控制.为了加快模型的收敛速度,减少离群点的影响,对数据记录中的物理协变量进行归一化处理[13],公式如下:

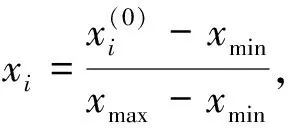
(1)

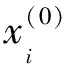
2 方法介绍

2.1 卷积神经网络原理

卷积神经网络是一种前馈式神经网络,由输入层、卷积层、池化层、全连接层及输出层构成,结构如图1所示．卷积层和池化层专门用来数据预处理,任务是过滤输入数据、提取有用的信息用作输入．卷积层在原始输入数据和生成新特征值的卷积核之间进行卷积运算．这种技术最初用于从图像数据集中提取特征[14],输入数据必须是结构化的矩阵形式．

相对于输入矩阵,卷积核(滤波器)被认为是一个小窗口,包含矩阵形式的系数值．这个窗口滑动整个输入矩阵,对输入矩阵中的指定窗口遇到每个子区域进行卷积运算．所有数据经过操作后的结果称为卷积矩阵,表示由系数值和应用滤波器的尺寸大小所指定的特征值[15]．通过对输入数据应用不同的卷积核,可以生成多个卷积特征,这些特征通常比输入数据的原始特征更重要,从而可以提高模型的性能．池化层从卷积特征中二次采样,提取特征值并产生低维矩阵,以减少网络的参数,提高模型的鲁棒性．通过上述类似的过程,与卷积层上执行的操作一样,池化层利用最小滑动窗口,将卷积特征的每个子区域的值作为输入并输出一个新的值．

表1 研究站点的地理特征和降水频率

图1 卷积神经网络的结构Fig.1 Architecture of convolutional neural network

2.2 注意力机制原理

将Attention机制(图2)加入神经网络中,考虑过去状态不同的影响因子,捕捉与日降水量相关的最重要部分．为了充分利用过去的状态信息,本文提出的CNN-Attention-BP组合模型在CNN层上增加一个注意力层,目的是降低甚至忽略与降水发生无关的信息,改变对重要信息的注意力．关键是对神经元分配不同的概率权重,使得模型更加注意到影响分类预测较大的数据信息以提高预测准确率[16]．

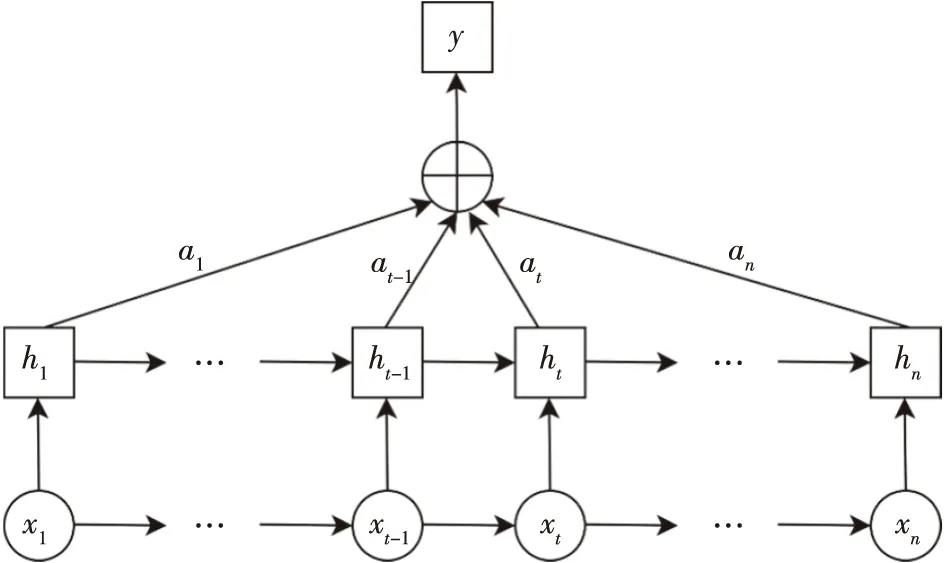
图2 注意力机制的结构Fig.2 Architecture of attention mechanism

2.3 BP神经网络原理

反向传播神经算法(Back Propagation Neural Network)简称BP神经网络,是一种基于误差反向传播的多层前馈网络．BP网络包括输入层、隐藏层、输出层,训练过程由网络信号的正向传递和误差的反向传递组成[17],结构如图3所示．前者为信号的前向传递,传递正方向计算输出值;后者采用梯度下降法调整权值和阈值来计算目标函数的最优值[18]．

2.4 CNN-Attention-BP组合模型

本文提出的组合模型结构主要分为Input层、CNN层、Attention层、BP层和Output层,流程如图4所示．

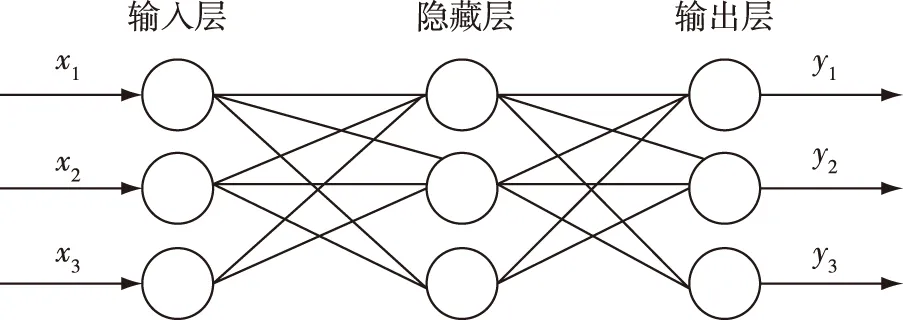
图3 BP神经网络结构Fig.3 Architecture of BP neural network

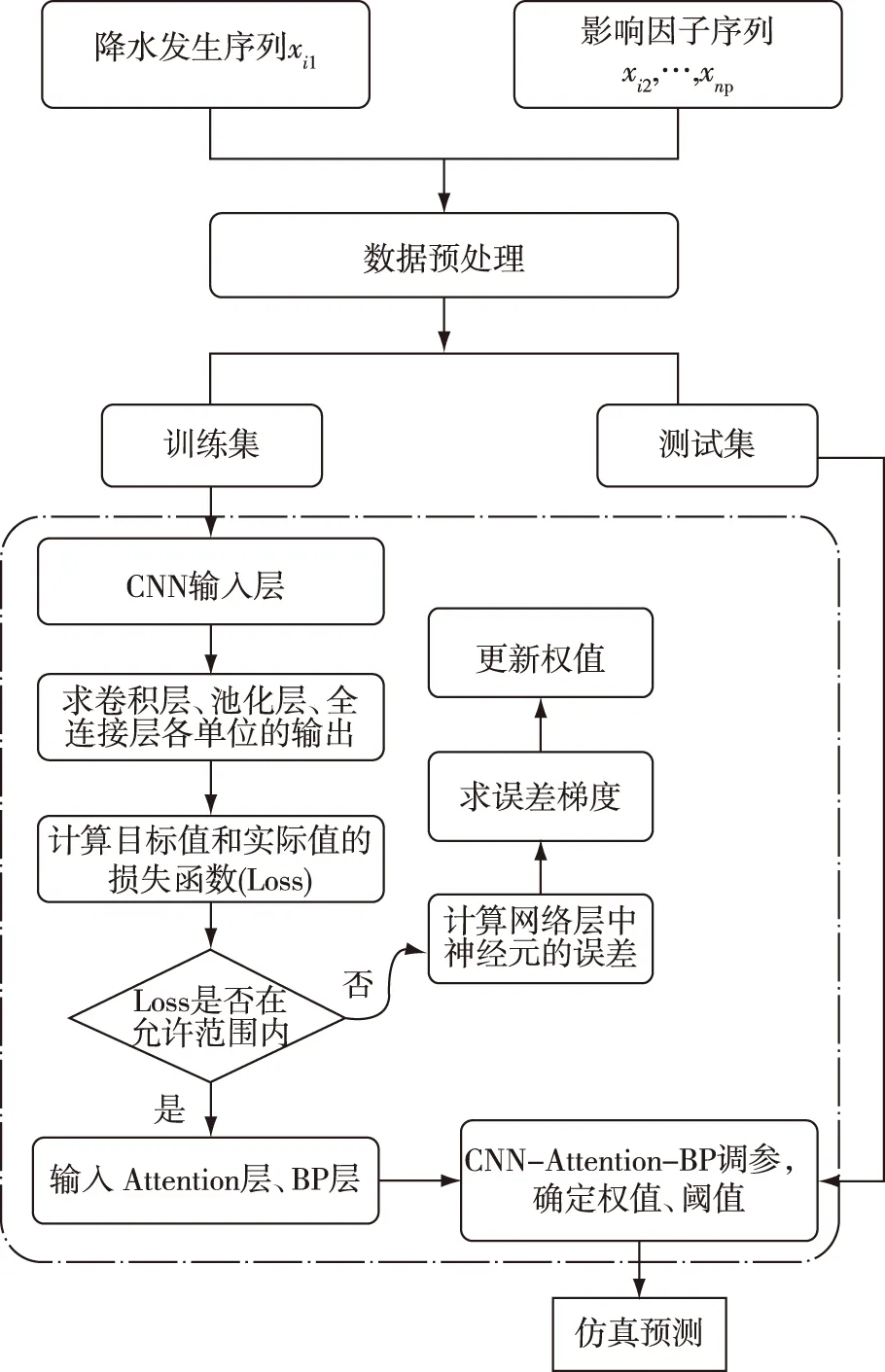
图4 CNN-Attention-BP组合模型流程Fig.4 Flow chart of the CNN-Attention-BP model

将降水相关的历史数据

作为组合模型的输入,xi1表示降水发生的标签值,i=1,…,n;xi2,…,xnp表示第p个影响因子归一化后的序列．首先经过卷积层连接一个非线性激活函数ReLU,然后选取常用的最大值池化进行运算,即提取池化层中元素的最大值．经过卷积层和池化层后原始数据被映射到隐层特征空间,再搭建选用Sigmoid激活函数的全连接层将其转换输出以解决降水分类问题,最后得到输出的特征向量[19]．

首先,将CNN层的输出特征向量Yc表示为

Z1=f(X⊗W1+b1)=ReLU(X⊗W1+b1),

(2)

F1=max(C1)+b2,

(3)

Z2=f(F1⊗W2+b3)=ReLU(F1⊗W2+b3),

(4)

F2=max(Z2)+b4,

(5)

Yc=f(F2×W3+b5)=Sigmoid(Z2×W3+b5),

(6)

式中:Z1,Z2分别为第1层和第2层卷积的输出;F1,F2分别为池化1层和2层的输出;W1,W2,W3为权重矩阵;b1,b2,b3,b4,b5为偏差;⊗和max()分别为卷积运算和最大值函数;CNN层输出的长度为t;Yc=[Yc1,Yc2,…,Yct]T．

然后,将经过CNN隐藏层激活处理后的向量Y作为Attention层的输入,经非线性转化成et表示第t个样本经过CNN层输出向量ht的特征状态矩阵,如式(7):

et=utanh(wlht+b),

(7)

u和wl为权重矩阵,b为偏置矩阵．其次,对每一个变量赋予初始权值,再通过softmax层进行归一化得到注意力权重,计算方式如下:

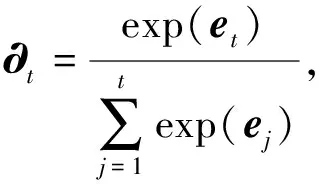
(8)

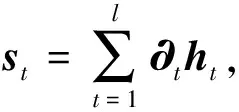
(9)

其中,∂t为注意力向量,st为Attention层在第t时刻的输出．

将经过CNN、Attention层后的输出向量记为Xc=[xc1,xc2,…,xcl]T,表示l维的BP神经网络输入向量,Y=[y1,y2,…,ym]T表示预测值,初始化权重值Wpq,Wqk以及隐含层阈值aq和输出层阈值bk后,进行前向传播与后向传播．本文在BP各隐含层节点使用Sigmoid激活函数,则神经节点l输入表示为

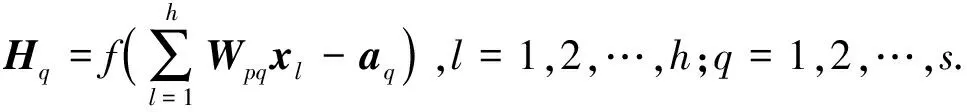
(10)

式中l为隐藏层节点数,f为隐藏层激励函数．经过隐藏层得到预测模型的输出:

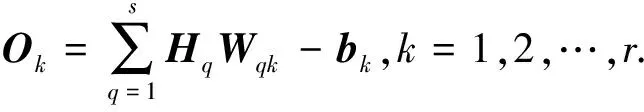
(11)

当Yk为实际值,有误差函数:

ek=Yk-Ok.

(12)

最后,计算输出目标向量和实际值的误差．若全局误差比设定的误差值小,固定当前的权重和阈值各参数值,学习结束,输出预测向量Y=[y1,y2,…,yf]T;若不在误差范围内,误差值进行反向传递以更新权值和阈值．

3 实例分析

3.1 组合预测模型的步骤

基于CNN-Attention-BP组合模型进行降水发生预测的过程可划分为两个阶段．第一阶段为 1960—2000年6—8月的训练阶段,第二阶段为2001—2020年6—8月的预测阶段．以长春站为例,改进后的卷积神经网络模型步骤如下:

Step1.将归一化后的长春站降水数据划分为训练集和测试集．

Step2.将已清洗的与降水相关的气象数据作为输入变量,实际降水标签值为输出变量,使用卷积神经网络方法进行训练．将训练周期(Epoch)设定为1,初始化的学习率为0.1,Batch_Size表示训练一次选取的样本数,初始设定为32,捕捉降水相关序列的特征．

Step3.在CNN隐藏层引入Attention进行训练,提取与降水发生相关性较强的气象数据．

Step4.再将Attention层的输出结果输入到BP神经网络中,实现对整个神经网络进行调参,输出预测向量和实际值的误差;若不在误差范围内,返回Step2再次计算误差梯度,更新权值,直至在误差范围内,训练结束,固定各参数值．随着Epoch的增大,准确率开始下降,所以选取准确率最高时的Epoch为9．由于批次过大会产生过拟合现象,故本文设定Batch为32、64、128和256.经过前期训练,当Batch为128时训练误差最小.更新学习率为0.000 1.具体见图5、图6．此时,BP的训练次数为10,学习率为0.002,批次大小为50．

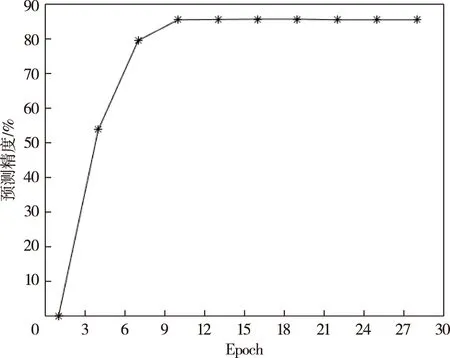
图5 模型在不同训练周期下的预测精度Fig.5 Forecast accuracy of the model with different epochs

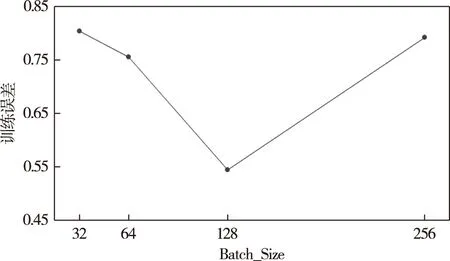
图6 模型在不同批次下的训练误差Fig.6 Training loss of the model with different Batch_Size

Step5.利用参数优化后的模型对测试集数据进行建模,完成对降水发生模型的预测．改进后的神经网络方法的参数设置如表2所示．

表2 改进的神经网络方法的参数

3.2 模型评价指标

本文在组合的预测模型训练过程中,选取 Adam (Adaptive moment estimation)[20]算法最小化目标函数,对神经网络参数进行优化．Adam算法能够基于训练数据迭代更新神经网络的权重,使损失函数输出值达到最优．同时,使用交叉熵损失函数(Cross-Entropy Loss Function)作为评判指标,即:

(1-yi)·log(1-pi),i=1,…,f,

(10)

式中,floss表示交叉熵损失函数,yi为样本的期望输出,pi为样本的实际输出．交叉熵其实是实际输出概率与期望输出概率的距离,即交叉熵的值越小,两个概率分布就越接近,损失就更小．

仅使用交叉熵损失函数不能充分评估模型的性能,故选取可表明模型稳定性的准确率(A)以及评估模型泛化能力的F1-score(F1):

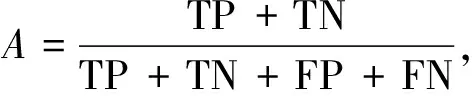
(11)

其中,TP表示正确预测为有降水的样本数,TN表示正确预测为无降水的样本数,FP表示错误预测为有降水的样本数,FN表示错误预测为无降水的样本数．

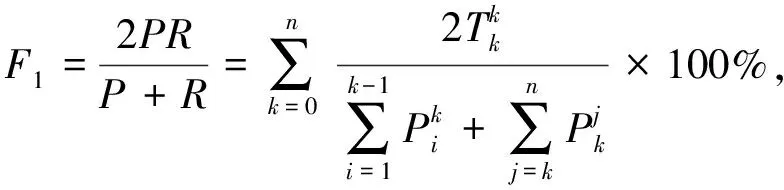
(12)

其中:

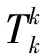
3.3 预测结果与分析

本文选用吉林省1961—2020年夏季6—8月的20—次日20时降水量、平均本站气压、平均风速、平均气温和平均相对湿度数据来进行组合模型的训练和测试．根据不同的气候类型选择具有代表性的长春站、白城站、延吉站为研究站点,使用SVM、MLP、单一的CNN和组合的CNN-Attention-BP方法分别对降水发生模型进行预测．其中,1961—2000年6—8月的气象数据作为训练样本,2001—2020年6—8月观测资料用于预报效果的检验．

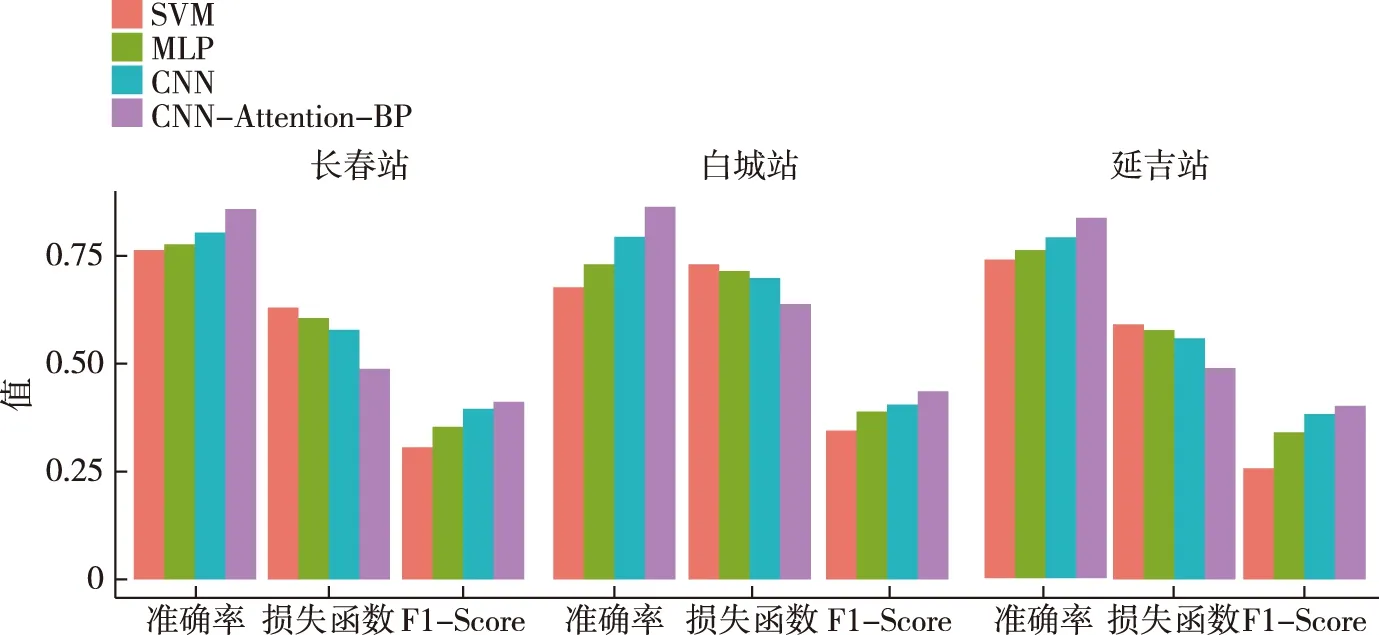
图7 代表性站点不同模型的性能Fig.7 Performance comparison of different models for the studied stations

将上文提到的SVM、MLP、单一的CNN和CNN-Attention-BP方法的评估结果进行对比．从图7可见:改进后的CNN组合模型相较于其他单一的模型具有更高的预测精度,准确率均大于80%;在损失函数直方图中,CNN-Attention-BP具有更小的损失,尤其在可表明模型综合性能的F1-score指标中,本文提出的方法具有更高的神经网络模型的质量．在不同站点,新的组合模型准确率更高,损失更小,效果明显优于单一模型．

根据定义可知,准确率越高表明模型具有更好的预测精度．从表3的预测结果中,延吉站的CNN-Attention-BP组合模型的准确率最高达到88.4%,相对于其他单一模型至少提高4.9个百分点.交叉熵损失函数的值越小,损失就更小,表明实际输出概率与期望输出概率的距离越近．延吉站组合模型的交叉熵损失函数最小为52%,相较于其他方法最多降低10.5个百分点;F1-score综合考虑模型的精准率与查全率的计算结果,在SVM中F1-score最低达到27.4%,MLP、CNN以及CNN-Attention-BP对应的F1-score分别为35.9%、40.1%、42.4%．CNN-Attention-BP组合模型的F1-score最高,表明优化后的CNN质量更高．

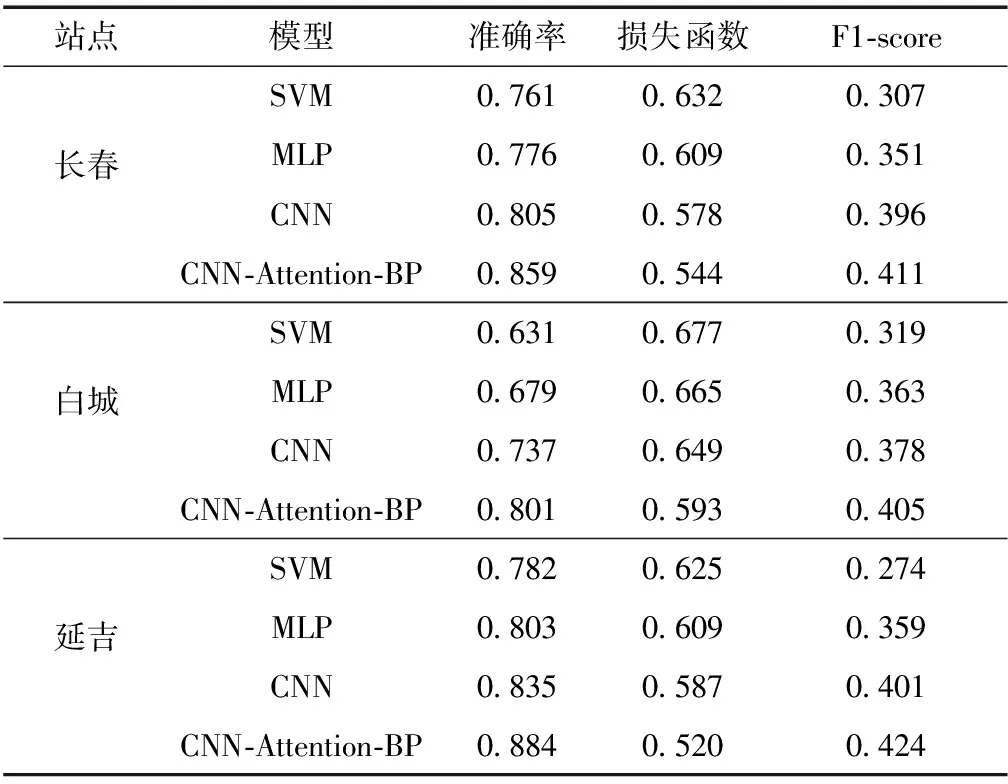
表3 代表性站点不同模型的预测性能

对于长春站的夏季降水发生模型,CNN-Attention-BP组合模型的准确率最高可达85.9%,相较于SVM方法提高9.8个百分点,相较MLP方法提高8.3个百分点,相较CNN方法提高5.4个百分点;交叉熵损失函数最高可降低8.8个百分点;在F1-score方面,组合的CNN-Attention-BP模型最稳定为41.1%,SVM最低为30.7%．

在白城站,CNN-Attention-BP的准确率最高达到80.1%,相对于单一的CNN模型提高6.4个百分点．此站点的准确率比其他站点低,是因为白城属温带大陆性气候,降水整体偏少,降水频率只有0.36,表明无降水与有降水的总天数存在不平衡,即正负样本数量的不均衡,导致传统的统计模型不能较好地学习其降水特征,而优化后的卷积神经网络可以快速地学习降水数据特征并找到重要信息进行训练.交叉熵损失函数相对于其他方法至少降低5.6个百分点;F1-score在SVM中最低为31.9%,MLP、CNN以及CNN-Attention-BP对应的F1-score分别为36.3%、37.8%、40.5%．综合分析,改进的卷积神经网络方法的预测准确率较为稳定,在交叉熵损失函数和F1-score指标上都有明显的改进,表明组合的降水发生预测模型具有更好的性能．

4 结论与讨论

由于降水发生事件的不确定性,本文提出一种基于CNN-Attention-BP的组合模型,将复杂的降水发生预测任务进行分解．先采用卷积神经网络有效地学习与降水有关的气象信息进行特征提取,进而利用Attention机制对重要的信息进行权重分配,最后,使用BP对整个网络进行参数调整以达到最优的预测结果．对吉林省代表性站点的夏季降水发生进行预测,结果表明:基于不同气候类型的夏季降水发生相关序列,在温带大陆性气候、降水频率为0.36的白城站,本文提出的CNN-Attention-BP组合模型在准确性方面,准确率最高可提高17个百分点;在衡量降水发生和不发生概率分布距离的损失函数指标中,最高降低8.4个百分点;代表模型泛化能力的综合性指标,F1-score至少降低2.7个百分点．在降水频率近0.5的长春站、延吉站,准确率最高可达88.4%,损失函数最低为52%,F1-score最高为42.4%．比较代表性站点的性能评价指标,新的组合模型在降水发生预测方面稳定性和准确性更好,具有较好的适用性．