耦合MBSs三量子点输运性质研究

秦 芳

(河北民族师范学院 物理与电子工程学院，河北 承德 067000)

Majorana费米子是一种遵循Non-Abelian统计的任意子，极适合构建量子比特,应用于拓扑量子计算，此外Majorana费米子还可能是暗物质的一种备选粒子。因此从提出起就引起人们的广泛关注。遗憾的是至今仍然没有发现以单粒子形式存在的Majorana费米子。理论预言在拓扑超导体的涡核或同时存在超导性和强自旋轨道耦合的纳米线末端存在着一种性质类似于Majorana费米子的准粒子—马约拉纳束缚态(MBSs)[1-2]。但大多数拓扑超导体都需在很低的温度下实现，难以制备异质结构。近期，Zhang、Wang等人发现铁超导体FeTe0.55Se0.45表面满足拓扑超导电性的必要条件，在这种超导体中，通过观察由外部磁场引起的漩涡核心处的零偏压电导峰，可以更简单地观察到MBSs[3-4]。Liu等也通过隧穿谱中的零偏压电导峰发现 (Li0.84Fe0.16)OHFeSe可作为研究MBSs的理想平台[5]。由此可见，零偏压电导峰的存在是产生MBSs 的有力证据。此外，人们还利用4πJosephson效应、非局域量子隧穿等方法来探测MBSs。

理论上常将MBSs与量子点体系相耦合，通过耦合前后体系输运性质的变化来证明MBSs的存在[6-8]。文献[6]研究了耦合MBSs 单量子点体系的输运性质。结果表明，MBSs强烈影响通过量子点的电导。零温时，若纳米线处于拓扑相，电导峰值为e2/2 h；若纳米线处于平庸相，电导峰值为e2/h；若体系耦合一普通费米子，电导峰值为0。在文献[7]中，作者研究了两种模型的电导，在量子点—MBSs—量子点体系中，发现零费米能处电导等于e2/h，不随体系众多参量的变化而改变；研究量子点—量子点—量子点—MBSs体系发现，当量子点为偶数(奇数)时，零费米能处电导等于2e2/h(e2/h)。文献[8]将MBSs耦合到T型量子点体系的末端。研究表明，零偏压电导峰始终等于e2/2 h，该数值不随量子点的数目改变。

对比于单量子点和双量子点结构，三量子点作为耦合多量子点体系的最小结构单元有多种构型，不仅可以通过参量的设置实现单、双量子点体系的全部信息，还可以获得单、双量子点体系无法实现且有实际应用价值的输运性质，因此更具研究价值。本文将三个量子点排成一列，一对MBSs耦合在量子点1、2间，将这两个量子点各自与正常金属电极相连，利用非平衡格林函数的方法重点研究体系参量变化时MBSs对反射系数的影响。

1 模型

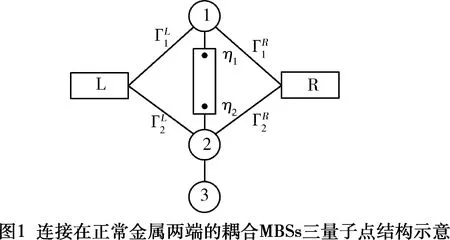
如图1所示，具有强自旋轨道耦合的半导体纳米线的两端分别与量子点1、2相连，并将该纳米线置于s-波超导体上，且沿纳米线的方向施加一均匀外磁场，则在适当的条件下两个局域的MBSs将会出现在在纳米线的两端[9]。两正常金属电极分别连接到量子点1、2 的两侧，量子点3与量子点2耦合。体系哈密顿：

H=Hdots+HLeads+HT+HM

(1)

其中：

(2)

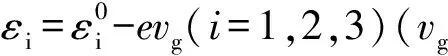
(3)

利用非平衡格林函数技术、Fourier变换及Keldysh公式可得从左电极流入的电流：

(4)

(5)

由于零温下系统的电导[10]

(6)

所以在接下来的讨论中只画出了反射系数随费米能的变化曲线。

2 结果与讨论

仅考虑ε1=ε2=ε3=ε0，εM的情况。

固定量子点1与MBS的耦合强度λ1，量子点2与MBS的耦合强度λ2取不同的值时反射系数随费米能的变化如图2(b)～(d)所示。图(a)为未耦合MBSs时反射系数曲线，图中出现三个峰值等于1的反射峰，分别位于E=0、E=±t处。这是由于此时量子点未与MBSs连接，因此没有拓扑超导体与之量子点相连，所以体系没有Andreev反射发生，TA=TH=0，图中出现的反射曲线仅由单电子遂穿产生。图(b)～(d)分别为λ2<λ1、λ2=λ1及λ2>λ1时的反射曲线，其中紫色和红色曲线分别为局域Andreev反射和交叉Andreev反射，蓝色曲线为单电子遂穿，黑色为系统总反射。当λ2<λ1时，Andreev反射出现5个反射峰，分别位于E=0、E≈±λ1和E≈±λ2处。由于同电极的Andreev反射TA贡献了两次，所以在对电导的贡献中这一项前乘以了系数2，恰好是交叉Andreev反射的2倍。当λ2=λ1时，Andreev反射仅余E=0一个峰。而当λ2>λ1时，其余两对峰再次出现。三种情况下零点Andreev反射峰的形状和大小始终没有发生变化，一直固定在0.25。TE曲线恰好与Andreev反射曲线的峰谷相反，即由于量子点与MBSs相耦合，单电子遂穿在Andreev反射峰位置发生了反共振，并且E=0处单电子遂穿系数恰好等于Andreev反射系数。这是由于量子点1、2分别与一个MBS(即“半个费米子”)相连，所以反共振并未使透射系数变为零，而是降为1/4。值得注意的是当量子点与MBSs耦合后，零点反射值始终等于1，不随λ2的改变而发生变化，体现了MBSs不受局域扰动的特性。为了进一步研究MBSs的这一特性，我们分别改变体系其它参量观察反射曲线的变化。

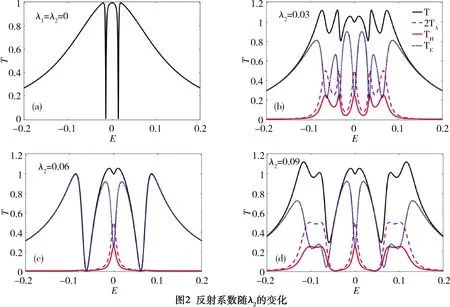
图3为反射系数随体系与电极间的耦合强度λ2的变化曲线。由图可见，T—E曲线呈现四个反射峰，主要由单电子遂穿导致，峰值位置不变，各峰宽度随着λ2的增加变宽。零点Andreev反射峰的变化与之相反，随着λ2的增大，一个尖锐的峰将该位置原有的平台取而代之。零费米能处反射系数仍然一直固定在1。

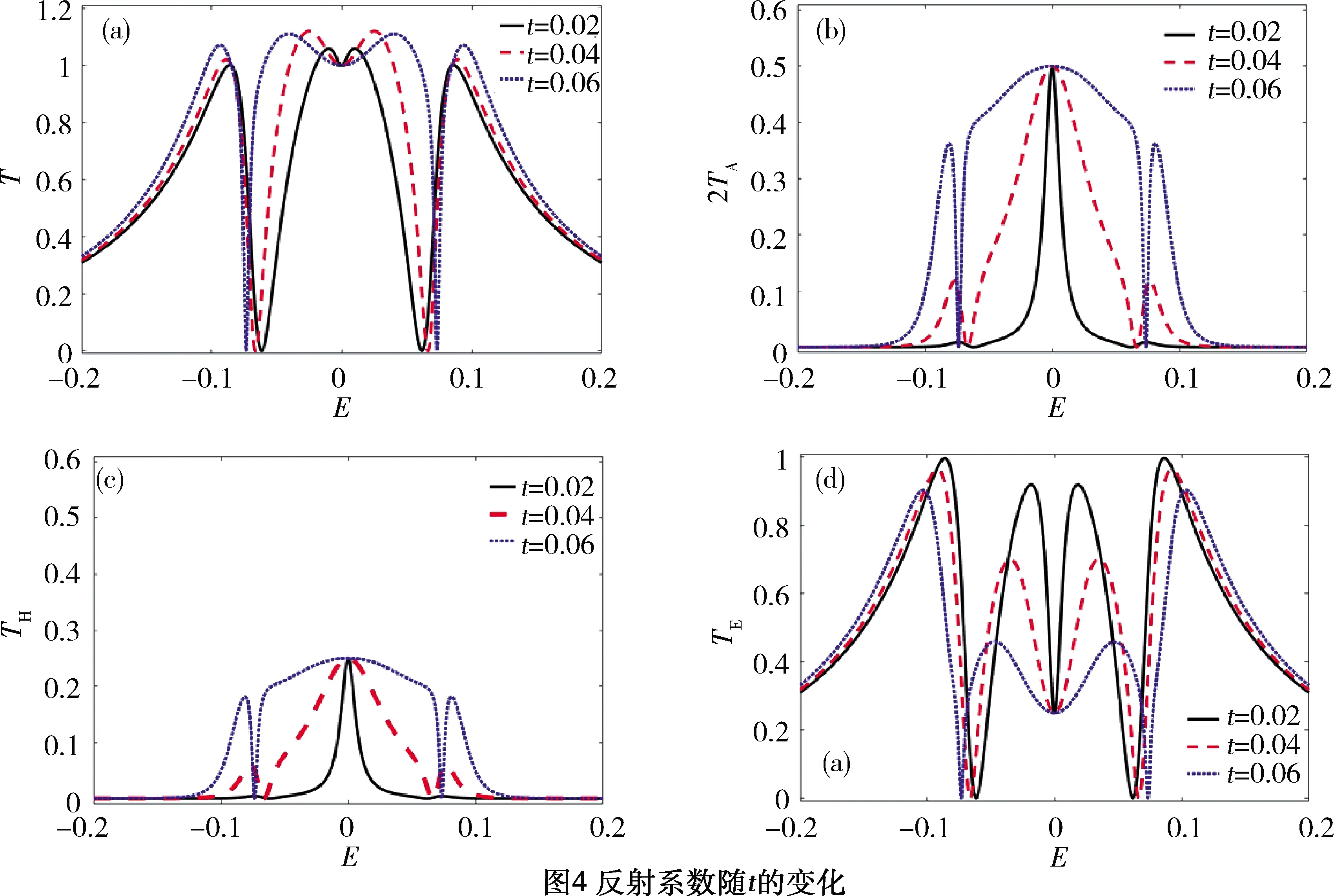
量子点2与量子点3间的耦合能t对反射系数的影响如图4所示。由图(a)可见，t对反射曲线的影响主要集中在零费米能附近，E=0两侧的峰值随着t的增大变宽。由图(b)、(c)可见，t对Andreev反射峰的影响明显，随着t的增大零点反射峰显著变宽，在其两侧一对新的对称反射峰逐渐出现，原本位于零费米能两侧的反射峰峰值变大，并分别向远离零点的两侧对称移动。单电子遂穿曲线的变化与Andreev反射曲线恰好相反，各峰值随着t的增大减小，峰值位置向偏离零费米能的左右两端稍有偏移。由此可见，随着量子点2与量子点3间的耦合能的增大，Andreev反射作用逐渐增强，由于单电子遂穿减弱，总反射曲线的各峰值几乎没有变化。零费米能处的各反射系数均没变化。

图5为改变量子点能量时反射曲线的变化。该组曲线明显不同于前面三组。首先，随着λ2的增加，反射曲线呈现出不对称的特点，观察图5(b)～(d)发现这一情况由单电子遂穿导致。在单电子遂穿曲线中零费米能的左侧出现了两个明显的Fano共振。其次，随着λ2的增加，零费米能处的Andreev反射值减小，而单电子遂穿反射值增加，由于二者变化的幅度相同，所以该点的总反射值依旧始终等于1。充分体现了MBSs的鲁棒性。

3 结论

本文利用非平衡格林函数方法研究了耦合MBSs的正常金属/三量子点/正常金属模型的反射系数随费米能的变化规律。结果表明，当体系耦合MBSs后，改变体系λ2、Γ和t，曲线呈对称分布，并且无论这些参量如何变化，总反射系数始终固定在1，Andreev反射系数始终等于0.5，是交叉Andreev反射系数的2倍，充分体现了MBSs的鲁棒性。当改变参量ε0时，由于单电子遂穿曲线中出现了两个明显的Fano共振峰，反射曲线呈现出不对称的特点。因此耦合MBSs后三量子点体系反射曲线新的特征可作为判别MBSs存在的重要依据。