基于机器学习的筒仓动态侧压力预测模型及概率分布研究
2022-05-18余汉华徐志军赵世鹏刘婷婷
余汉华,徐志军,赵世鹏,刘婷婷,原 方
河南工业大学 土木工程学院, 河南 郑州 450001
目前,在我国主要使用房式仓、筒仓等仓型储存粮食[1]。筒仓以其占地面积小、容量大、成本低、机械化程度高等优点在粮食仓储中有着广泛的应用。然而,筒仓损坏或倒塌的事故在国内外不断发生,其原因是在设计过程中没有充分考虑筒仓侧壁压力[2]。筒仓侧壁压力分为储存物料时的静态侧压力以及卸料时的动态侧压力。研究发现筒仓的动态侧压力大于静态侧压力,动态侧压力是导致筒仓结构失稳的重要原因[3-4]。
众多学者在对筒仓动态侧压力的研究中取得了许多有意义的成果。原方等[5]利用PIV技术观测了在卸料过程中粮食颗粒的细观运动,从理论上揭示了仓壁动态侧压力增大机理。Kobyka等[6]使用离散元法(DEM)模拟了粮仓的初始卸料,研究了稀疏-压缩波的传播,结果表明稀疏-压缩波是应力脉动的形成原因。Wang等[7]利用有限元方法(FE)预测料斗卸料中的动态侧压力,得出压缩波传播是应力脉动的原因。Wang等[8]通过有限元方法模拟了带有圆锥形料斗的筒形筒仓内壁的法向应力,研究表明,垂直、会聚过渡处的应力波动幅度大得多,同时提出这主要是由主应力从垂直方向到会聚方向引起的。刘克瑾等[9-10]通过数值模拟技术研究发现筒仓卸料时动态侧压力的增大与动态起拱有很大的关系。
然而,影响筒仓动态侧压力的因素较多,而各种影响因素之间存在着错综复杂的非线性关系。传统的研究方式,譬如Jassen公式,只考虑某一种或少数几种影响因素。因此建立一种能够考虑多种影响因素、高效、准确的动态侧压力的预测方法尤为重要。近年来,由于AI的快速发展,基于机器学习的方法在许多领域都获得了有益的成果。例如,作为机器学习的3个关键算法,随机森林算法、BP神经网络算法和支持向量机算法都可以进行数据分类和回归分析,以处理非线性、不确定性和小样本问题,在土木工程中具有良好的应用[11]。因此,作者利用支持向量机、BP神经网络和随机森林方法,提出了考虑多因素和非线性影响的筒仓动态侧压力预测模型。对3种预测模型的预测结果进行了比较分析,得出动态侧压力的最优预测模型。利用该模型研究了筒仓动态侧压力的概率分布。研究成果可为筒仓动态侧压力预测提供一种新方法,推动可靠度理论在筒仓结构中的应用。
1 机器学习理论
常见的机器学习主要包括监督学习、非监督学习、半监督学习以及强化学习,监督学习主要包括分类和回归2种任务。常用的回归方法有支持向量机算法、BP神经网络算法和随机森林算法等。
1.1 支持向量机算法
支持向量机算法是基于统计理论的,这种方法的优点是采用结构风险最小化的原则,其模型可以用式(1)表示[12]。
f(x)=ω·φ(x)+bf(x),
(1)
式中:x为输入特征向量;f(x)为输出值;φ(x)为映射到高维特征空间的非线性函数;ω为超平面的权重向量;b为偏置向量。
为了解决非线性回归问题,支持向量机就是求式(2)中函数的最优解[13]。
(2)
式(2)满足约束条件:
(3)
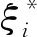
通过引入拉格朗日公式和Karush-Kuhn-Tucker条件,利用其对偶问题得到最优解。
(4)
式(4)满足约束条件:
(5)
式中:αi和αi*为拉格朗日乘子。
引入核函数K(xi,yj),可以解决支持向量机算法中的高维计算问题。径向基函数具有良好的预测精度,选用径向基函数作为核函数,给出核函数的表达式。
(6)
式中:σ为样本方差。
在式(4)满足式(5)的条件下,结合式(1)和式(6),则得出支持向量机的最终回归拟合函数。
(7)
本文采用LIBSVM工具箱[14]实现支持向量机预测。
1.2 BP神经网络算法
BP 神经网络(Back propagation neural network)是在神经网络的基础上发展起来的一种算法。目前,它主要应用于求解高维非线性问题。学习过程主要包括输入信息的正向传播和误差的反向传播。BP神经网络本质是一种多层前馈神经网络,也称为多层感知器。它是一种既没有规律也非线性的函数。输入层分别对应影响筒仓动态侧压力的9个影响因素(X1,X2,…,X9);输出层对应筒仓动态侧压力(Y)。BP神经网络的结构见图1,Wij和Vij表示权重。
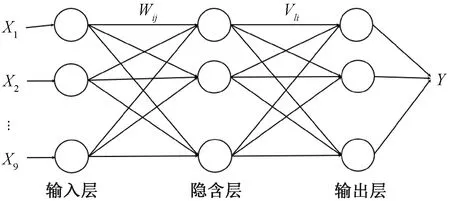
图1 BP神经网络结构
原始数据集决定了BP神经网络的输入层与输出层的神经元节点数,目前,一般使用经验公式来确定隐含层的节点数,主要经验公式有3种[15]。
(8)
h=log2m,
(9)
h=2m+1,
(10)
式中:h为隐含层神经元节点数;m为输入层神经元节点数;n为输出层神经元节点数;a为0~10之间的整数。
合适的隐含层节点数对BP神经网络的预测精度有着重要的影响,当隐含层节点数量较大时, BP神经网络的复杂度会增加,算法的整体学习效率会降低。
1.3 随机森林算法
随机森林算法的原理是针对原始数据集,采用Bagging算法进行不放回抽样,得到多个新的样本集,然后通过新样本集进行回归性决策树的构建。每棵决策树从训练样本的特征变量中选择一部分作为分裂标准,这些特征变量将被划分为多个设定的单元,每一个单元对应的是一个输出结果,再将建模过程中的样本集合进行分类,最终得到决策树的回归结果。在求解回归问题时,将所有计算结果的平均值作为随机森林回归预测模型的最终预测结果。
基于CART算法和Bagging算法的随机森林算法有2个独特的优势:第一,确定决策节点不需要历遍所有的样本数据,只需要从中选择一部分作为特征变量,利用平均绝对误差(MAE)和均方误差(MSE)确定最优分割节点;第二,Bagging算法在一定程度上降低了训练样本之间的相关性,既有效提高了随机森林回归预测模型的泛化能力,又减少了过拟合现象的发生,在决策树生长的过程中不需要进行剪枝的过程。因此,随机森林在进行回归预测时比传统的线性回归方法具有更高的运算速率、更快的分类速度、更少的参数调节等优点,特别是在求解高维非线性问题方面具有独特的优势。具体回归操作流程见图2。
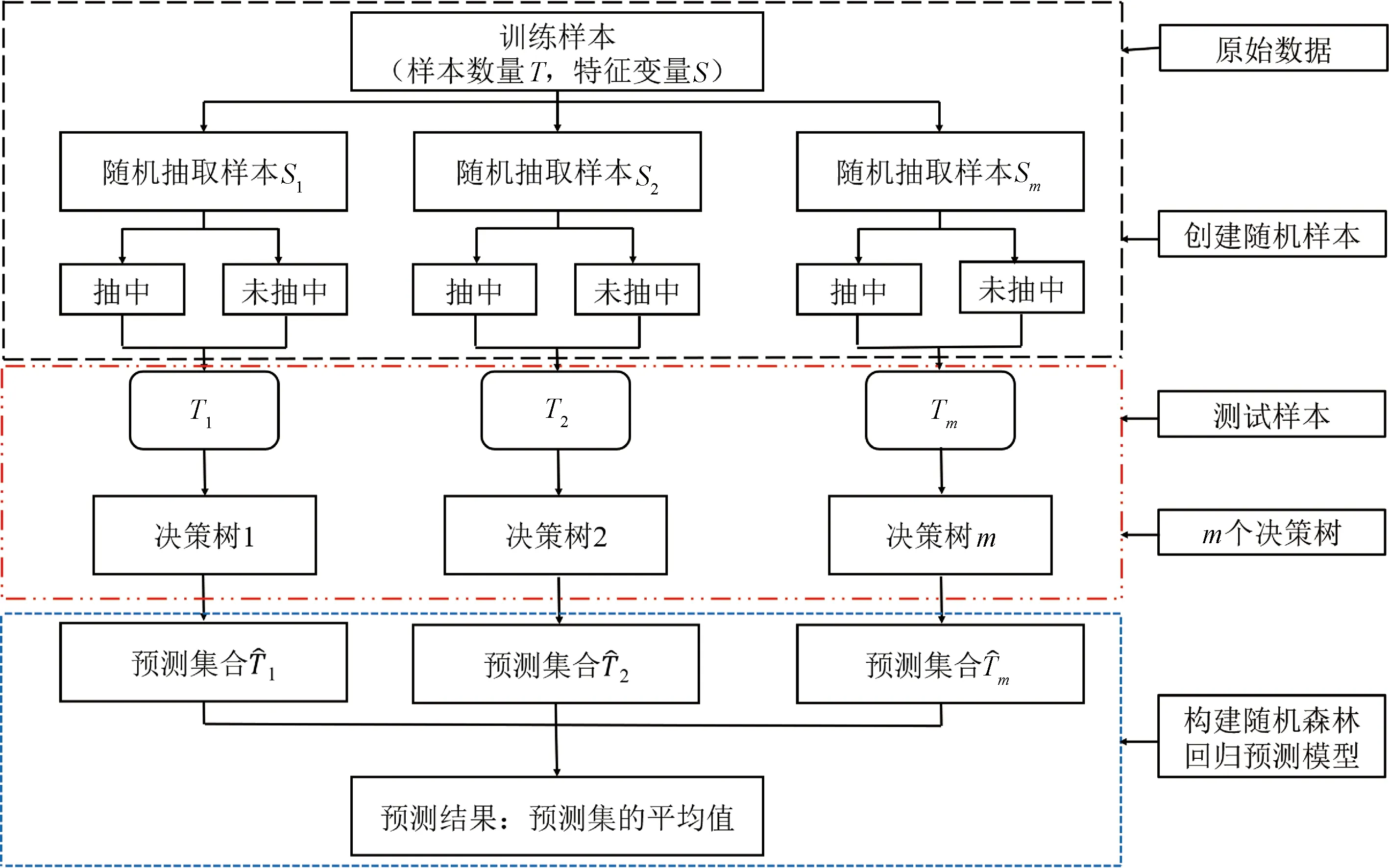
图2 随机森林回归预测模型操作流程
2 基于机器学习的筒仓动态侧压力预测模型
2.1 数据来源
PFC数值模拟数据能够作为筒仓设计和动态侧压力研究的依据。本文选用文献[16-23]中532组PFC模拟数据供机器学习预测模型选择,相关参数见表1。
2.2 数值模拟
机器学习的预测精度受数据量的影响,为了尽可能地扩大数据样本,除了从文献中采集的数据以外,基于表1数值,进行了24组模型筒仓卸料模拟,其中1~12组选择稻谷为贮料,13~24组选择大米为贮料,每组模型筒仓设置20个测墙共获得480组数据。建模时的相关参数见表2。

表1 相关参数
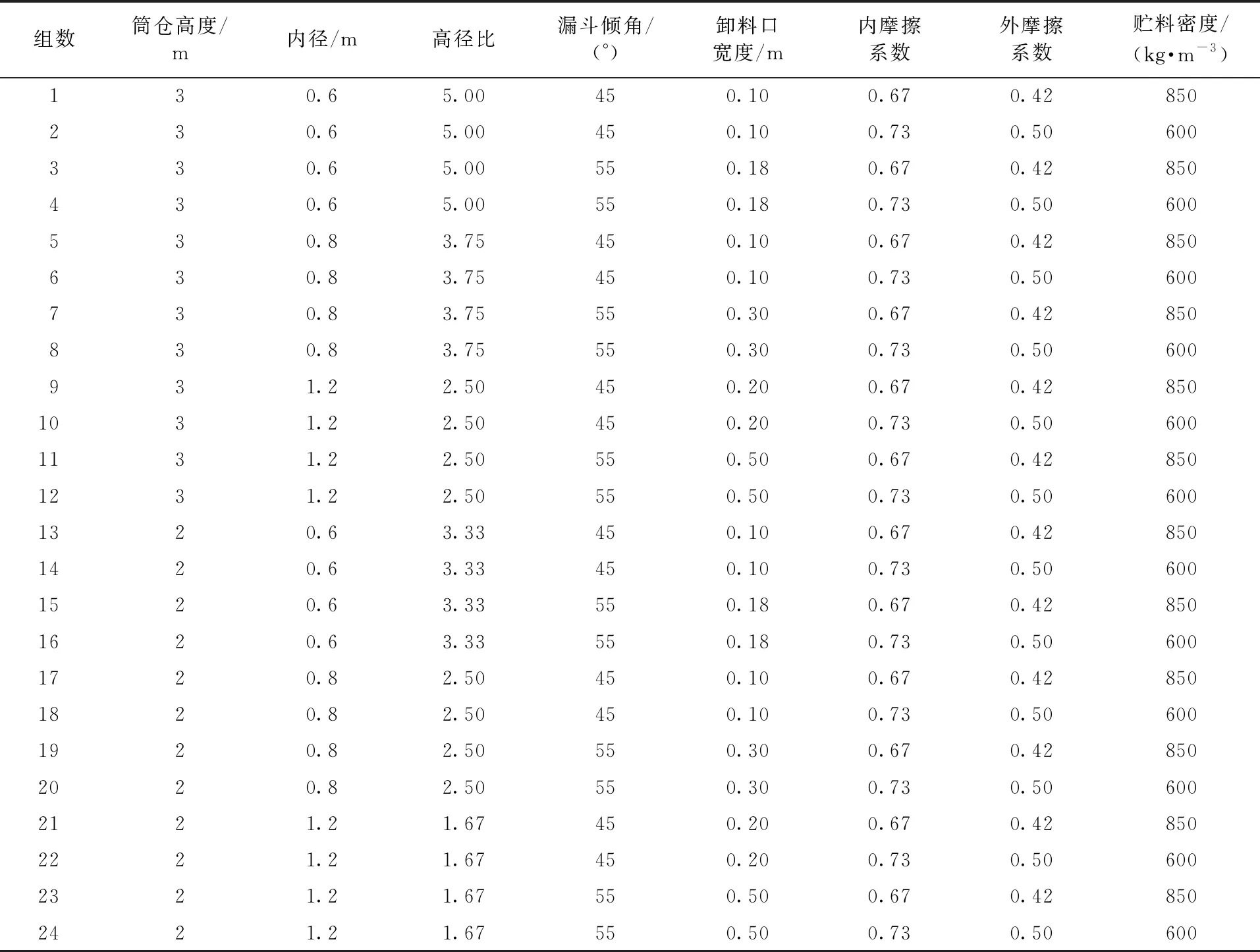
表2 来源模拟的相关参数
2.3 数据预处理
在进行机器学习前,数据需要进一步归一化。利用式(11)将文献搜集数据和数值模拟数据集中的输入变量和输出值归一化到[0, 1],900组数据作为预测模型的训练样本,其余数据作为测试样本。
(11)
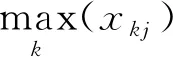
2.4 构建预测模型流程及参数设置
筒仓动态侧压力预测模型的输入量为筒仓高度、内径、高径比、卸料口宽度、漏斗倾角、内摩擦系数、外摩擦系数、贮料密度以及测点位置,输出量为每个测点处的最大动态侧压力值。分别采用支持向量机、随机森林和BP神经网络3种机器学习方法建立了筒仓动态侧压力预测模型。模型构建流程如图3所示。
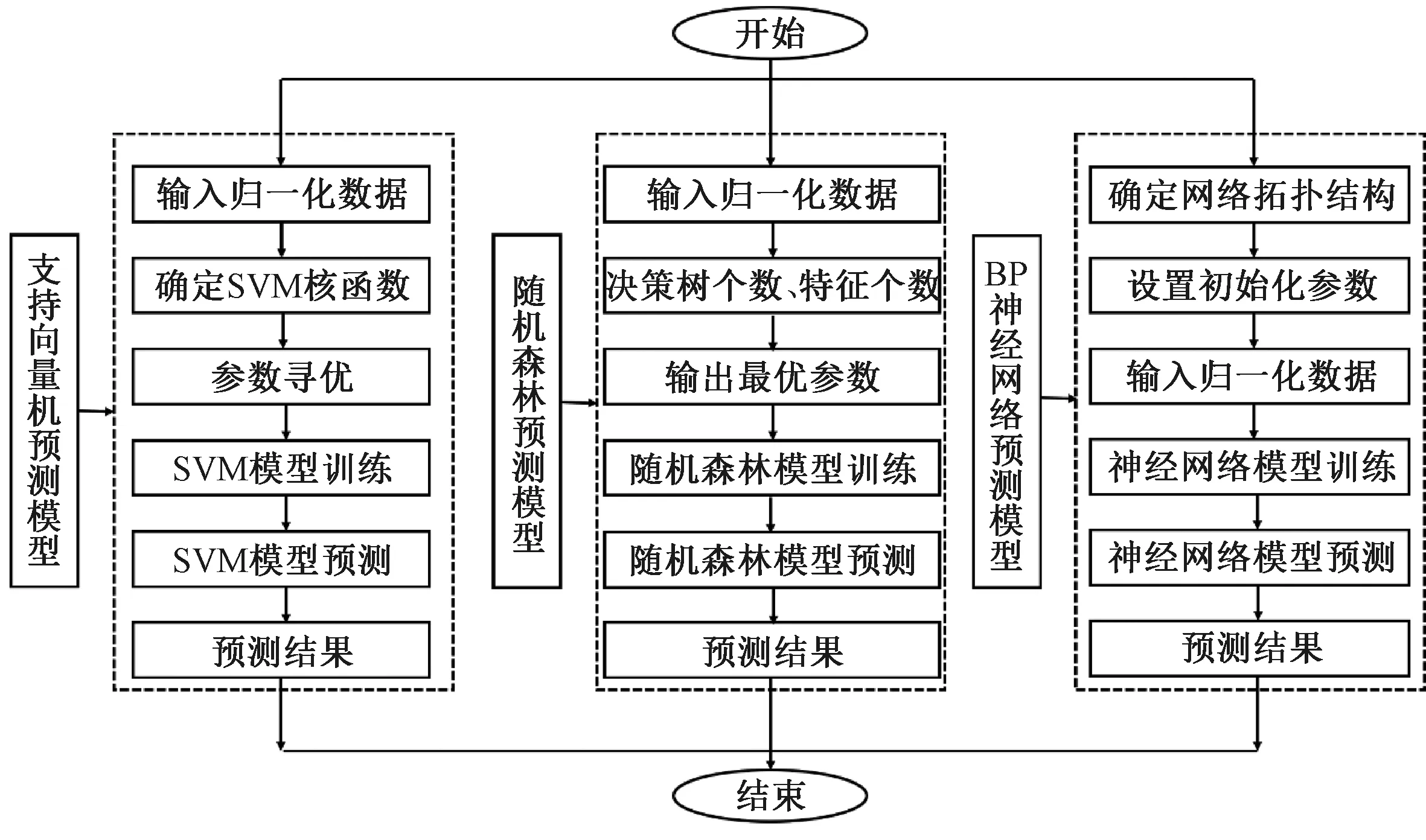
图3 基于机器学习的筒仓动态侧压力预测模型流程
预测模型的重要步骤是确定模型的相关参数。设置支持向量机惩罚参数为2.828 4,核函数为8;设置随机森林决策树个数为5,特征个数为500;神经网络设置激活函数为“Tansig”函数,学习率为0.001,期望误差为0.001,训练次数为1 000,隐含层神经元节点数为8。
2.5 预测结果
对相关参数进行设置后,分别代入3种预测模型,为了验证3种模型最终的预测能力,将76组试样的预测值与真实值进行对比,结果如图4—图6所示。
基于表1和表2中的数据及图4—图6,对3种算法的绝对误差进行计算,见图7。
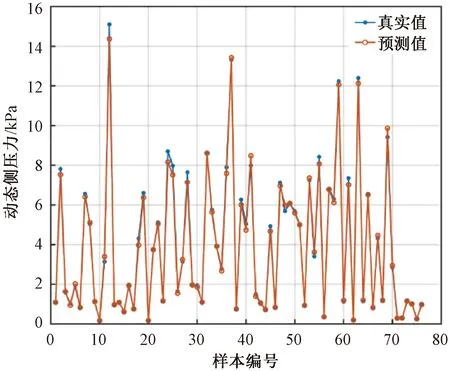
图4 基于支持向量机的筒仓动态侧压力预测模型的回归拟合
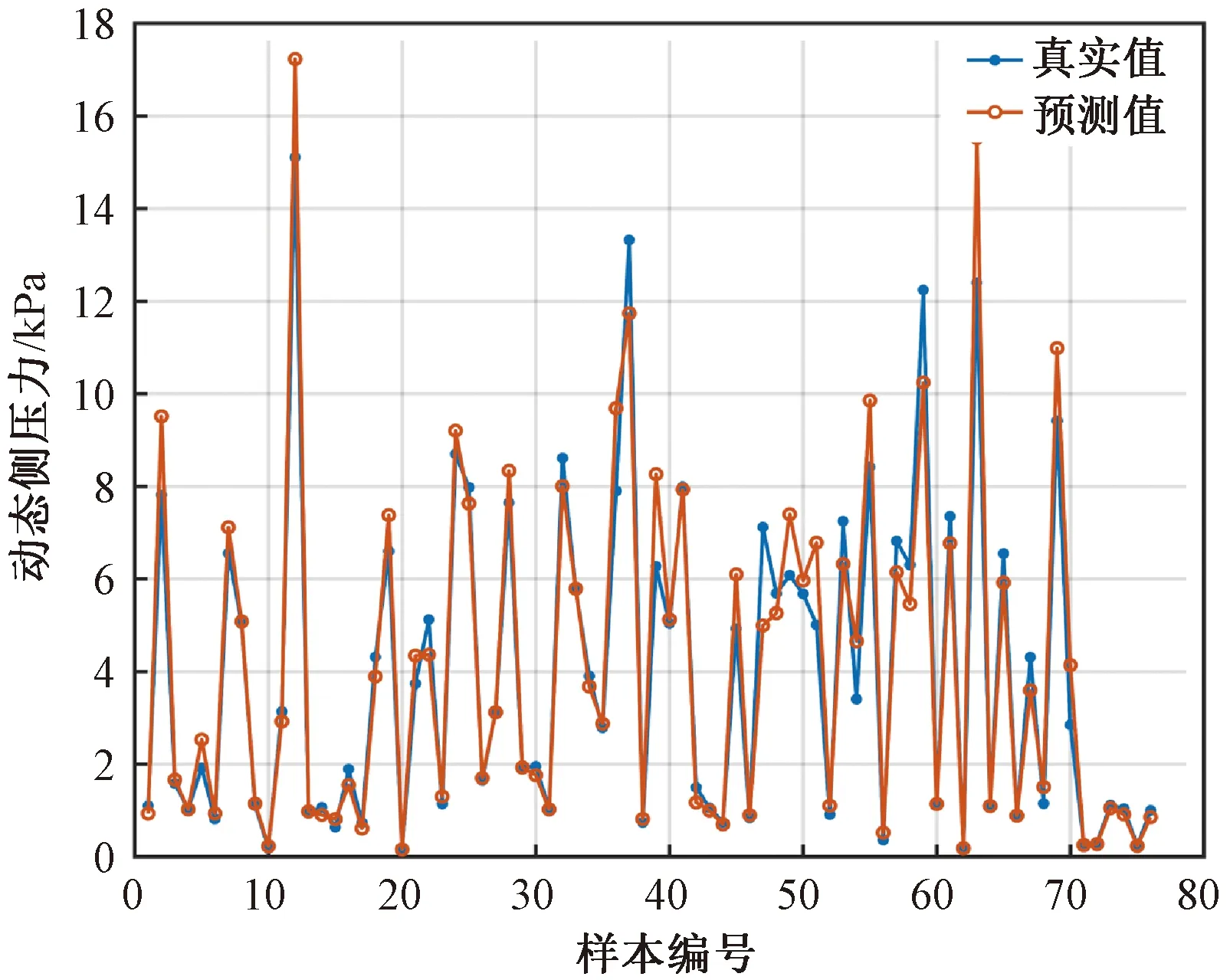
图5 基于随机森林的筒仓动态侧压力预测模型的回归拟合
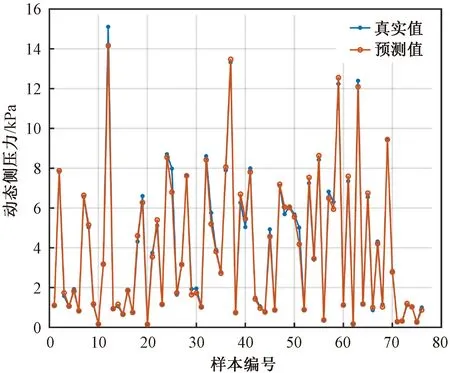
图6 基于BP神经网络的筒仓动态侧压力预测模型的回归拟合
从图7可看出,基于支持向量机的筒仓动态侧压力预测模型的数据绝对误差值较为集中,离散的点较少。基于BP神经网络的筒仓动态侧压力预测模型的数据绝对误差离散点较多。基于随机森林的筒仓动态侧压力预测模型的数据绝对误差较前2种预测模型较大,突出的离散点最多。因此,基于支持向量机的筒仓动态侧压力预测模型误差最小、精度最高。本文采用支持向量机对筒仓动态侧压力的概率分布进行了研究。
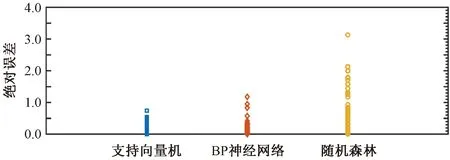
图7 3组模型数据绝对误差对比
3 基于支持向量机模型预测
3.1 生成随机数
本文选用小麦的物理属性进行研究。根据规范可知,小麦的密度介于681.5~804.0 kg/m3,平均值为750 kg/m3,小麦的密度可以作为随机变量。随机数的生成采用均匀分布的方法,该过程主要通过MATLAB计算中的Rand函数来实现。最终得到1 000组小麦密度的随机数,随机数服从均匀分布且平均值为750 kg/m3。
3.2 预测结果
筒仓卸料过程中,筒仓高度为5 m,内径为2 m,高径比为2.5,卸料口宽度为0.06 m,漏斗倾角为45°,内摩擦系数为0.4,外摩擦系数为0.4,测点位置为筒仓底部1/3处。将以上固定值代入上述的支持向量机预测模型中,同时将已编号的1 000组小麦密度的随机数代入上述模型,得到的预测结果见图8,图中的1个小圆代表一组数据。
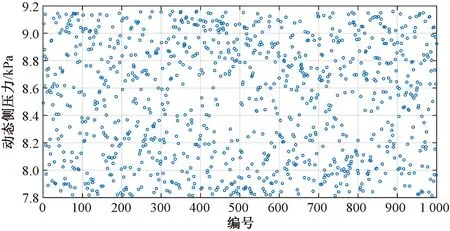
图8 支持向量机预测结果
筒仓设计规范中将小麦的密度规定为800 kg/m3,通过Janssen公式得到此时的动态侧压力为9.13 kPa,因此将9.13 kPa视为筒仓能够承受的最大动态侧压力。由图8可知,1 000组数据中有39组数据大于9.13 kPa,在小麦密度规范取值范围内,不安全的概率为0.039,安全概率极高。因此,在筒仓符合设计规范的情况下,符合粮食规范的小麦不会引起筒仓事故。因此,预测结果可用于研究筒仓动态侧压力的概率分布。
3.3 Easyfit拟合概率分布函数
选择Easyfit软件对1 000组筒仓动态侧压力预测结果进行分析,步骤如下:1)首先将支持向量机预测的1 000组数据输入Easyfit软件的数据栏中,并点击对应的命令图标。2)选择自动拟合分布函数,选择Easyfit软件中的Beta分布。3)通过Easyfit软件将Beta分布的概率密度曲线与动态侧压力直方图进行绘制,结果见图9。初步得出筒仓动态侧压力服从Beta分布。
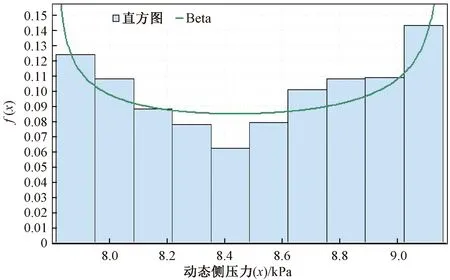
图9 直方图与Beta分布概率密度曲线
综上所述,支持向量机的预测结果能够用于筒仓动态侧压力概率分布的研究,为筒仓的可靠性分析提供一种新的思路与研究基础。
4 结论
建立了基于支持向量机、BP神经网络和随机森林的筒仓动态侧压力预测模型,结果表明:基于支持向量机的筒仓动态侧压力的绝对误差范围最小,说明基于支持向量机的筒仓动态侧压力预测模型的泛化能力最好,且预测精度最高。
在固定其他影响因素的条件下,获取1 000组均匀分布的小麦密度的随机数,利用构建的支持向量机预测模型获得1 000组预测结果。其中动态侧压力最大值大于筒仓规范计算结果9.13 kPa,在小麦密度规范取值范围内不安全的概率为0.039。
通过Easyfit软件进行拟合分布与优度检验,得出筒仓底部1/3处的筒仓动态侧压力最优概率分布为Beta分布,为筒仓可靠性研究奠定了一定的理论基础。
