集成学习方法的已实现波动率预测和偏度信息含量研究

王云润，乔高秀

(西南交通大学 数学学院，成都 611756)

0 引言

金融资产的波动率是衡量市场风险的重要指标，在资产的定价和分配、风险管理和货币政策制定方面都起着重要作用。因此，对波动率的预测在金融计量学研究中受到了极大关注。Bollerslev［1］提出了广义自回归条件异方差(GARCH)模型，该模型能捕捉到波动率聚集效应等，但其估计大多基于日数据。随着对日内高频数据的可获取，Andersen 等［2］提出将已实现波动作为对高频波动率的度量，以便更好地观测和评估波动率。为了刻画已实现波动的长记忆性，Corsi［3］引入异质性自回归(HAR)模型，该模型由于结构简洁、估算容易在研究界被广泛使用。Byun 等［4］将风险中性偏度直接作为解释变量加入HAR 模型，发现风险中性偏度包含已实现波动和隐含波动率中没有包含的信息，这些信息有助于波动率预测。其中，隐含波动率是由期权的市场价格倒推出的波动率，反映了投资者对标的资产未来波动率的预期。Mei 等［5］将已实现偏度加入HAR 模型中，发现已实现偏度对未来的波动率有明显的负面影响。样本外结果表明，已实现偏度有助于中长期预测，但无法提高短期预测的准确性。郑振龙等［6］在比较偏度和峰度对波动率的影响时，发现期权隐含偏度所包含的信息要多于基于历史信息的已实现偏度，对波动率的影响更显著。

在金融预测领域，传统研究假定经济系统是稳定的。但是，受到政治、经济和环境等多方面因素的影响，金融市场数据可能因为一些极端事件引起结构突变，使得时间序列的数据特征受到影响，从而导致参数不稳定性和模型不确定性。在数据存在结构突变时，通常使用突变后的数据进行预测，而数据有限使得模型存在较高的不确定性。因此，金融预测研究的最大挑战来自于考虑市场发生结构突变时存在预测模型的不确定性和估计参数的不稳定性。Pesaran 等［7］认为这可能不会使均方预测误差最小化，故在参数不确定性建模时，Dangl 等［8］和Zhu 等［9］使用时变参数模型，允许参数随时间变化;Wang 等［10］提出时间加权最小二乘回归方法，通过为距离预测时间越近的样本赋予越高的权重来解决参数不稳定性。Zhang 等［11］继Pesaran 等［7］和Pesaran 等［12］之后，使用窗口平均预测方法(AveW)，将在不同估计窗口长度上计算的同一模型进行平均，通过与其他预测方法比较发现，该方法能提高股票收益预测效果，在参数不稳定和结构突变情况下具有简单而可靠的特点。

尽管已有文献考虑到将偏度引入HAR-RV 模型，但尚无研究系统地比较过不同偏度指标所包含的信息差异和对波动率的预测能力。本文中主要探讨风险中性偏度，基于日内高频数据和日数据的不同偏度指标对已实现波动预测能力的信息差异，从这一新的角度对已有研究进行补充。在预测方法上，首先基于单个机器学习方法［13］预测已实现波动。考虑到市场结构突变导致的模型不确定性和参数不稳定性，且已有研究提出基于时间维度的改进方法来提高收益率预测效果［10-11］，因此将这一思想应用到数据驱动的机器学习算法中，充分考虑金融时间序列数据的时间维度特征，对距离预测点越近的样本给予更多的关注，并与传统的集成学习方法［14］相比较，从而提出具有更高预测精度的集成学习方法。

本文结构安排如下:第2 节介绍各种偏度指标和扩展模型以及研究方法;第3 节为实证结果，包括相关性分析、参数估计结果、每个方法的预测结果等;第4 节为稳健性检验，通过调整训练集长度来验证方法是否具有稳健性;第5 节为结论。

1 方法和模型

1.1 已实现波动和波动率的偏度指标

根据Andersen 等［2］的方法，通过将相应的高频日内平方收益相加得出每日已实现波动，计算式如下:

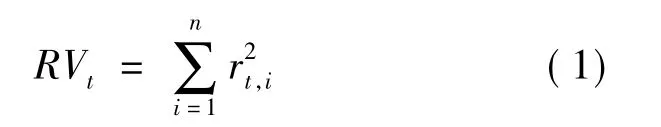
其中:rt，i表示第t 天，第i 次交易的对数收益。

Andersen 等［15］证明了已实现波动有以下极限结果:

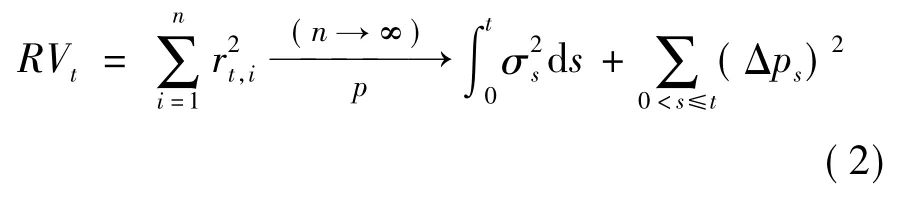
其中:Δps=ps-ps-表示在s 时刻跳的大小。

根据Barndorff-Nielsen 等［16］的研究，将已实现波动分解为已实现上半变差和已实现下半变差，定义如下:

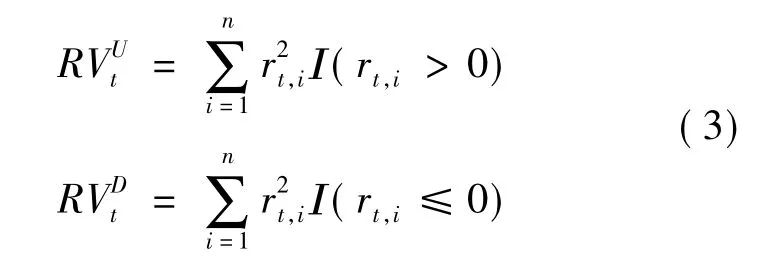
并且证明了:

其中:I(*)表示示性函数，易知已实现波动RVt=。

使用4 种不同的方法来刻画波动率偏度:

1)参考郑振龙等［6］的研究，利用m 个交易日的日对数收益率滚动计算已实现偏度(RSt)，计算式如下:

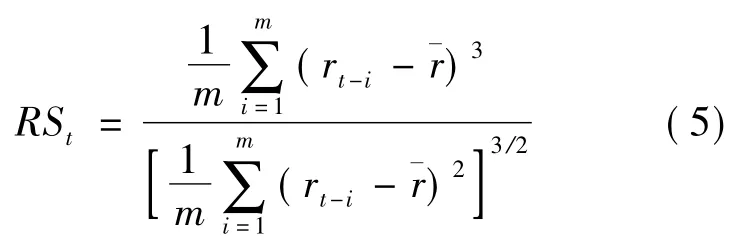
其中:rt为第t 天的日对数收益率;为m 个交易日的收益率均值，m 取值为22。

2)根据Chen 等［17］的研究，基于日收益率滚动计算负偏度(NRSt)为:

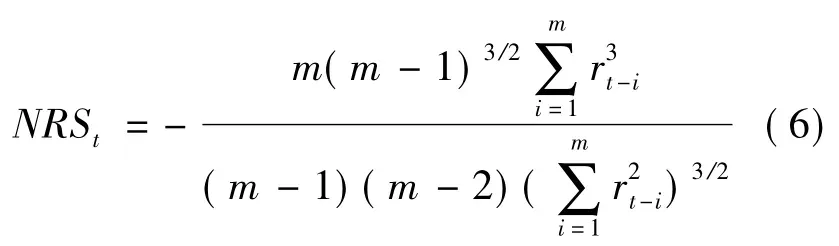
其中:rt定义和m 的取值同上。

3)参考Amaya 等［18］的研究，基于日内高频收益计算已实现偏度为:

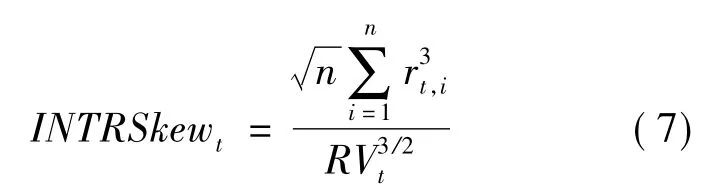
Barndorff-Nielsen 等［16］和Mathieu 等［19］的研究结果表明:

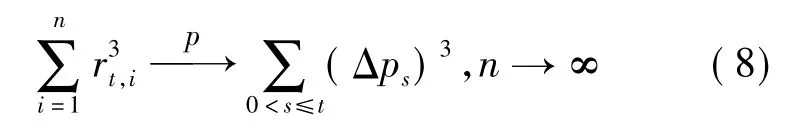
根据Feunou 等［20］提供的理论支持，可将已实现上半变差与已实现下半变差之差看作是上述已实现偏度(INTRSkewt)的一种度量，记为波动率偏度(RSVt)。计算如下:

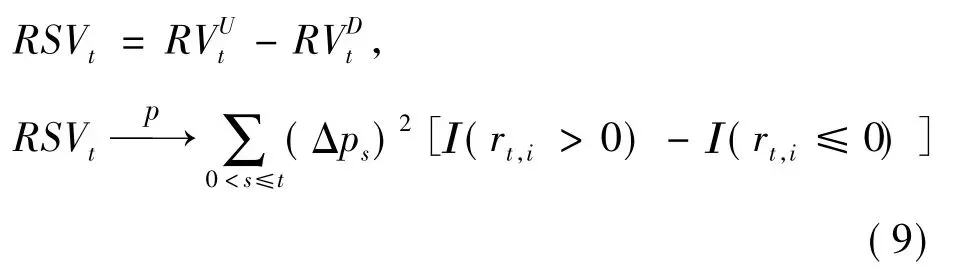
当RSVt＜0 时，收益率分布是左偏的;当RSVt＞0时，则分布是右偏的。

4)芝加哥期权交易所(CBOE)于2011 年推出风险中性偏度指数，记为QSt，计算如下:

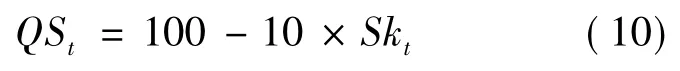
其中:Skt=，表示风险中性偏度;为S＆P 500 对数收益;μ=，σ=分别是其在风险中性测度Q 下的期望和标准差，其具体计算方式参考文献［21］。可以看出，RSt越小，左偏越明显;而NRSt和QS 越大，左偏越明显。

1.2 模型设定

使用由Corsi［3］提出的HAR 模型研究已实现波动的预测。由于该模型能很好地刻画资产收益波动率中的长记忆特性，且模型仅包含代表日、周和月效应的3 个变量，易于处理，因此该模型是已实现波动预测最受欢迎的模型。本文中采用对数回归，模型设定为:

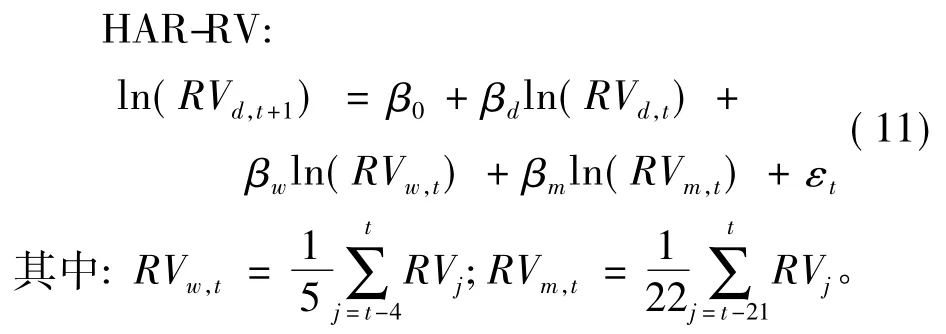
为了比较以上几种偏度指标包含的信息对已实现波动预测的差异性和准确性，分别将上述4种偏度指标加入HAR-RV 模型，设定如下:

1.3 研究方法

1.3.1 支持向量回归

传统的线性回归方法只要真实值与拟合值不相等就计算误差，而在支持向量回归［22］方法下，仅当二者之差的绝对值大于某个正数ε 时才计算损失，相当于以拟合值为中心，构建了一个宽度为2ε 的间隔带。若训练样本落入间隔带中，则认为是预测正确。

支持向量回归的求解表示为:

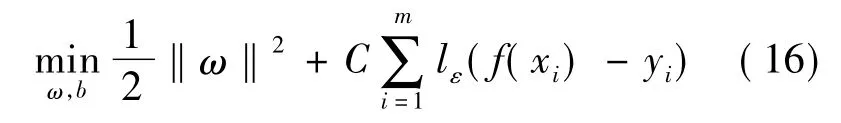
其中:C 为正则化常数;lε为ε-不敏感损失函数，表示为:

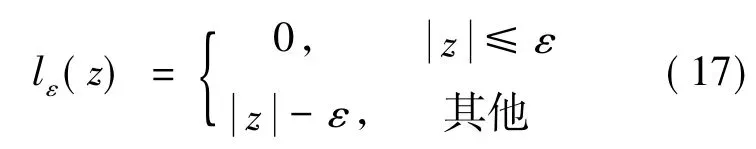
通过拉格朗日乘子法和对偶问题可以得到SVR 的解为:

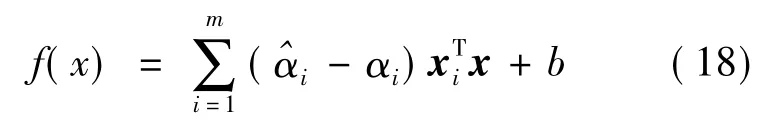
若考虑到特征映射形式，则对应的核函数SVR 解形式为:

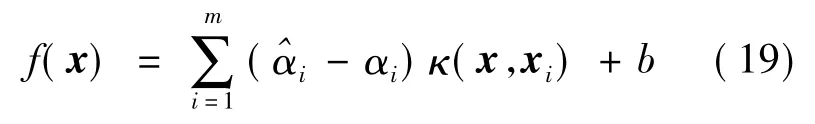
其中κ(xi，xj)=φ(xi)Tφ(xj)为核函数，φ(x)表示将x 映射后的特征向量。本文中选取的核函数为径向基(RBF)核函数，其定义为κ(x，z)=。采用五折交叉验证法和网格搜索法相结合来选取最优参数组合［23］。

采用同模型(11)—(15)一致的输入变量和输出变量构建SVR 模型。以模型(11)为例，具体形式如下:

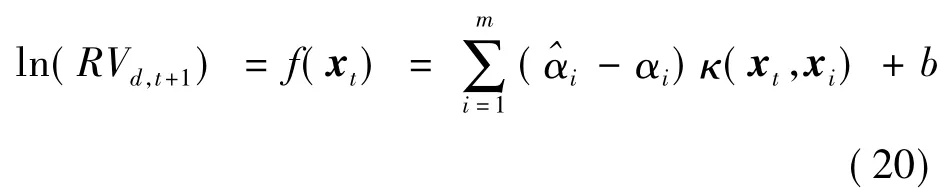
其中:x·=［(ln(RVd，·)，ln(RVw，·)，ln(RVm，·)］T。

1.3.2 带惩罚项的线性回归

在普通最小二乘回归基础上，引入带惩罚项的线性回归来解决简单回归分析可能产生的过拟合问题，即在最小化损失函数中加入惩罚函数φ(β)，形式为:

根据φ(β)的不同，采用岭回归(ridge regression)和弹性网络方法(elasticnet)［24］，φ(β)形式分别表示为:

其中:λ 为正则化参数，控制着模型的复杂度，λ 过大容易欠拟合，太小容易过拟合;α 为0～1 的正数，控制着L1 和L2 范数的比重;当α=1 时，此时弹性网络退化为套索回归;当α=0 时，则退化为岭回归。由此可见弹性网络结合了岭回归和套索回归的共同特点。

1.3.3 集成学习

集成学习先通过已有的学习算法从训练集中训练得到个体学习器，再将若干个这样的个体学习器通过某种方法结合，最终得到一个强学习器。根据个体学习器之间是否存在强依赖关系，分为串行生成的序列化方法和可同时生成的并行化方法，二者的代表方法分别是Boosting 和Bagging。

1)Adaboost 方法

本文中采用Boosting 族算法中最具代表性的Adaboost 方法［25］，并在处理回归问题时用平方误差来衡量误差率。在最后进行个体学习器集成时，用各个体学习器的预测结果乘以各自权重再求和作为最终结果。算法过程如下:

步骤1初始化训练数据的分布权重:D1=(w11，w12，…，w1i，…，w1m)，w1i=，i=1，2，…，m;

步骤2使用某个学习算法训练具有权重D1的训练集，得到第1 个基本学习器;

步骤3计算基本学习器T1(x)在训练集上的预测误差率e1:

Ⅰ)计算训练集上的最大误差:E1=，i=1，2，…，m。

Ⅱ)采用平方误差，计算每个样本的相对误差e1i=，i=1，2，…，m。

Ⅲ)计算回归预测误差率:e1=。

步骤4计算基本学习器T1(x)的投票权重α1，并更新第2 轮训练集的权重D2:

步骤5对第2 轮权重样本再次训练得到第2个基本学习器，重复上述过程N 次，得到N 个基本学习器T1(x)，T2(x)，…，TN(x)和相应的权重α1，α2，…，αN，则:

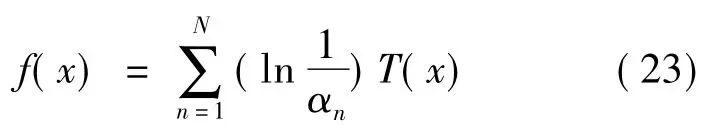
其中:T(x)是所有αnTn(x)的中位数(n=1，2，…，N)。

Adaboost 方法的本质是不改变训练数据，改变训练数据权重分布，每一轮训练提高前一轮误差大的样本权重;最后加权平均得到预测值，误差率越低的基本学习器权重越高。

2)Bagging 方法

Bagging 方法［26］是并行式集成学习方法中最著名的代表。采用自助采样法，即从包含n 个样本的数据集中随机取出一个样本放在采样集中，再将该样本放回数据集，使之在下次采样时仍有机会被选中，这样随机放回采样m 次，然后重复N次该过程，即可得到N 个含有m 个训练样本的采样集;对每个采样集训练得到一个基本学习器，对于分类问题用简单投票法，对于回归问题用简单平均法。

3)窗口平均预测法

除上述2 种集成方法外，本文中采用窗口平均预测方法(AveW)［7，11］。该方法可以看作是固定取样的Bagging。Bagging 集成预测方法在获得采样集时，由于自助采样法的随机性，对于时间序列预测来说可能并不是最优选择。而AveW 方法在不同估计窗口上拟合相同模型，并对模型的预测结果求平均。即终止日期相同，根据起始日期的不同获得若干个窗口长度不同的训练集，在这些训练集上训练得到基本学习器，将这些基本学习器的预测结果简单平均作为最终结果。窗口平均预测法的优势是充分考虑数据在纵向时间维度上的特征，时间越近的样本利用率越高，信息挖掘越充分。

以SVR 的窗口平均为例(记为 SVR +AveW)，用数学语言描述为:将给定的训练集作为最长的观测窗口W=，其中m是训练集长度，xt与2.3.1 部分提到的一致。首先，将W 分为N 个训练窗口:

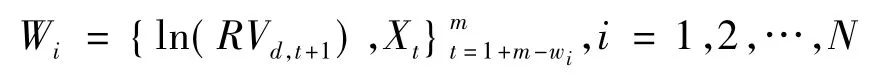
其中:wi=wmin+，wmin为给定的最小的训练窗口。Wi由最小窗口逐步递增到最大窗口。

然后，在每个Wi训练窗口上利用SVR 进行拟合，得到N 个拟合结果，i=1，2，…，N。则SVR+AveW 预测结果为:

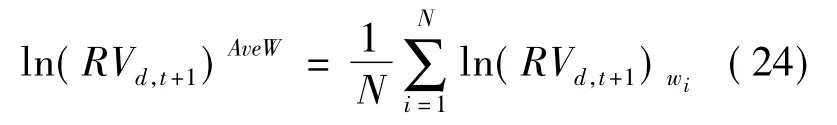
传统的OLS 背后假定经济系统是稳定的，Zhang 等［11］在预测股票收益率时考虑市场系统结构发生突变时模型的不确定性和参数的不稳定性，发现窗口平均预测方法能有效提高股票收益率的预测效果。与Zhang 等［11］的研究不同，本文中分别在线性OLS、带惩罚项的线性回归和非线性SVR 方法预测的基础上采用窗口平均集成预测方法来研究已实现波动预测。采用固定窗口大小的滚动估计，对于每个估计窗口，都用窗口平均预测法来向前一步预测已实现波动。

2 实证分析

2.1 描述性统计

数据选取标准普尔500 指数从2000-02-04 到2019-12-31 共4 983 个交易日数据。数据来自https://realized.oxford-man.ox.ac.uk/，风险中性偏度数据来源于芝加哥期权交易所网站。由于QS 的数值全部大于100，由式(10)可知，式中S 均小于0，因此QS 实际上刻画的是左偏风险。由于左偏风险与市场崩盘风险更直接密切相关，也为了与QS 保持一致，本文中对其余3 个偏度指标进行处理，提取RS 和RSV 中小于0 的部分并取绝对值，大于0 的部分赋值为0;对NRS 中小于0 的部分赋值为0，保留其大于0 的部分。RS-、RSV-和NRS+分别表示按上述处理之后的偏度;RS、RSV和NRS 分别表示未经处理的偏度。

表1 给出了处理后的各个偏度指标和已实现波动自然对数的描述性统计结果。RS-和NRS+均为基于每日收益的偏度指标，可以看出，二者在数量级上相比于另外2 个指标差别不是很大，差异主要由指标本身计算公式引起，即由中心化调整和前面系数的调整引起，在数据特征上均呈现右偏厚尾;RSV-的量级由于基于已实现波动数据本身的原因，仍然是右偏厚尾，而QS 则是右偏瘦尾。由JB统计量可知，所有指标均不服从正态分布。

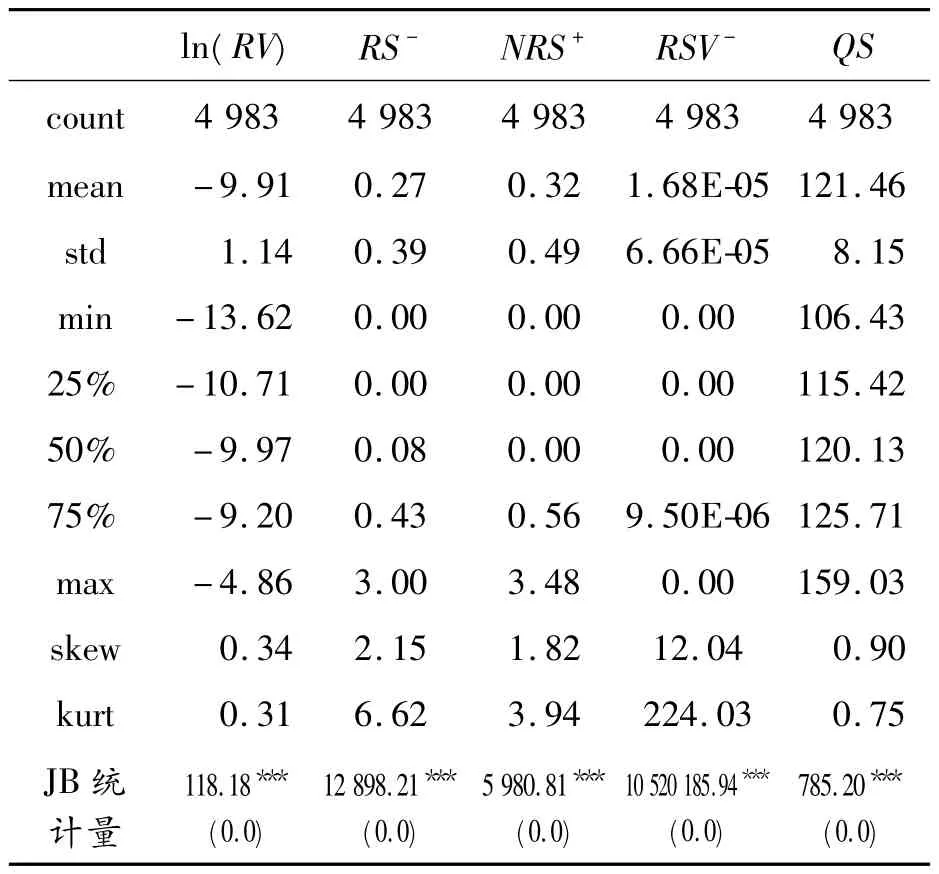
表1 各个变量的描述性统计结果

通过表2 得知，已实现波动与4 个偏度指标均存在一定相关性，但相关性方向不尽相同，证明偏度指标所包含的信息也存在一定的差异。

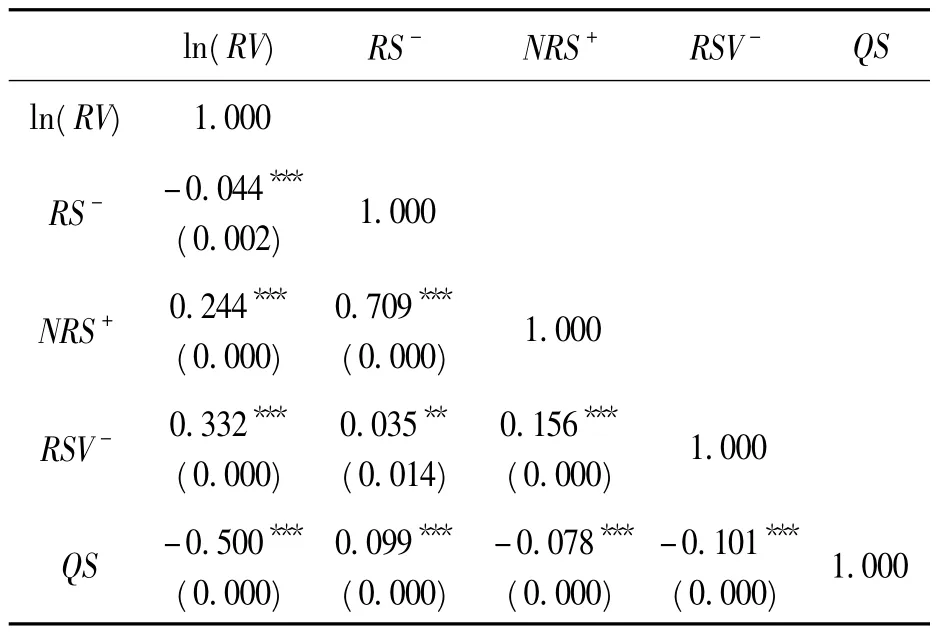
表2 各个变量间的皮尔逊相关系数

2.2 参数估计结果

表3 给出了式(11)—(15)的最小二乘估计结果，在进一步放宽显著性水平和有效位数的前提下(即可近似认为在10%显著性水平下RS-对已实现波动有显著影响)，可以确定各个偏度指标对已实现波动预测确实有显著性影响，但QS 的回归系数与其他3 个偏度指标的回归系数方向不同，因此QS 对已实现波动的影响与基于历史数据的3个偏度指标的影响不同，进一步证实了各个偏度指标包含着不同的信息。后续将考虑用不同方法来比较不同偏度指标对已实现波动的预测能力。

表3 普通最小二乘回归(OLS)参数估计结果

2.3 多种机器学习方法与波动率预测

本文研究中，重点关注不同方法对样本外已实现波动的预测效果。因此，将前70% (3 488个)的数据(2000 年2 月4 日至2014 年1 月16日)作为样本内数据，用于训练模型;将2014 年1月17 日至2019 年12 月31 日的1 495 个数据作为样本外数据，用于预测。采用以下2 个损失函数来评估模型的预测能力:

1)平均绝对误差:

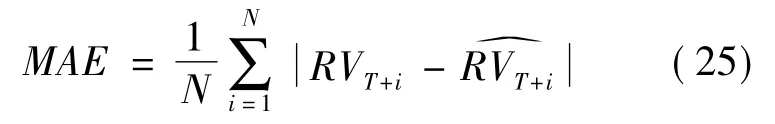
2)均方根误差:

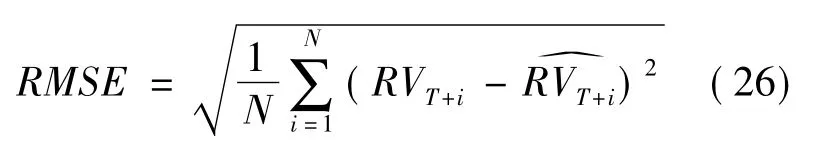
其中:T 表示样本内的观测点个数;N 是样本外滚动窗口的长度;和RVT+i分别表示波动率的预测值和真实值。

表4 给出了OLS、Ridge、ElasticNet 和SVR 估计方法的预测误差。由于带惩罚项的线性回归没有表现出比OLS 更好的预测效果，因此表4 中集成方法只给出在基于OLS 和SVR 的Adaboost、Bagging 以及窗口平均(AveW)的预测误差。方法上，对相同偏度的不同方法预测中，可以看到SVR的预测误差明显低于ElasticNet、Ridge 和OLS，说明非线性的SVR 方法优于本文所选取的3 种线性回归方法;在基于OLS 和SVR 的集成方法中，窗口平均预测法均有明显提升，其中基于SVR 的窗口平均预测效果最佳。比较不同偏度的预测能力时，综合比较各个方法得出:QS 对已实现波动的预测能力最强，基于日数据和日内高频数据的偏度指标对已实现波动预测没有特别明显的改善;仅将QS 加入HAR-RV 模型时，模型性能才有提升，说明QS 包含已实现波动中没有的信息，并有利于预测。

表4 测试集长度比例为30%时不同方法下各个偏度模型的预测误差

2.4 MCS 检验

采用MCS 检验来进一步验证上述结果。MCS检验常用于评价不同模型的预测能力［27-28］，根据Hansen 等［29］的研究，其检验统计量为:

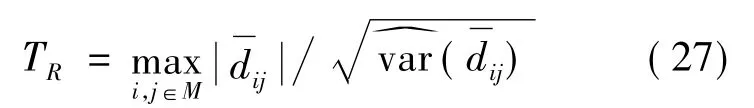
其中:模型i 与模型j 是来自模型集合M 任意2 个互异的模型;dij表示其损失差，表示模型i 与模型j 的平均损失;的自举估计。MCS 检验程序为初始设置中的每个模型分配P 值。对于给定的模型i，MCS 的P 值确定模型是否属于MCS 的阈值置信水平，当且仅当≥α 时(i∈，α 为显著性水平)，越大的模型预测能力越强。

表5 给出了测试集长度比例为30%时的MCS检验结果。MCS 检验的模型集合M 分为2 种情形:①相同方法之下，5 个不同HAR 模型预测误差所组成的模型集合(见Panel A);②相同模型之下，10 种方法的预测误差组成的模型集合(见Panel B)。由A 部分可以看出，在2 种误差标准下，对于单个方法而言，除了基于OLS 的Bagging方法是HAR-RV 模型最优外，其余9 种方法均为加入风险中性偏度(QS)的结果最优。因此，将风险中性偏度(QS)加入到HAR-RV 模型能提高模型对已实现波动的预测能力，而基于历史信息的偏度对模型几乎没有提升作用;B 部分表示在2 种误差标准下，对于不同的模型，其结果均为基于SVR 的窗口平均预测方法最优。可以看出，MCS检验结果与上述表4 的预测结果一致。

表5 测试集长度比例为30%时2 种情况下的MCS 检验结果

3 稳健性检验

上述结果基于测试集长度占样本总长度的30%得到。为了验证其是否具有稳健性，表6 给出了测试集长度比例为50%时不同方法下各个偏度的预测误差。以MAE 为衡量标准时，不同方法的最小误差均出现在QS;以RMSE 为衡量标准时，QS 在OLS、Ridge、ElasticNet 这3 种方法下预测误差小于NRS+，而其余7 种方法则是NRS+的预测结果略优于QS。因此，综合2 种标准可认为QS 的结果略优于NRS+。

表7 给出了MCS 检验结果。由A 部分可以看出，以MAE 为衡量标准时，除SVR+Bagging、SVR+AveW 外，其余8 种方法下，均为HAR-RVQS 模型明显优于HAR-RV-NRS+模型;而以RMSE 为衡量标准时，同理可以得出，HAR-RVNRS+略优于HAR-RV-QS，但综合比较A 部分的2个误差标准可知，HAR-RV-QS 模型表现优越的情况居多，因此认为当测试集长度比例为50%时，QS 的结果要略优于NRS+。由B 部分可以看出，在2 种误差标准下的最佳方法仍为基于SVR 的窗口平均(SVR+AveW)，MCS 检验结果和表6 预测误差结果一致。

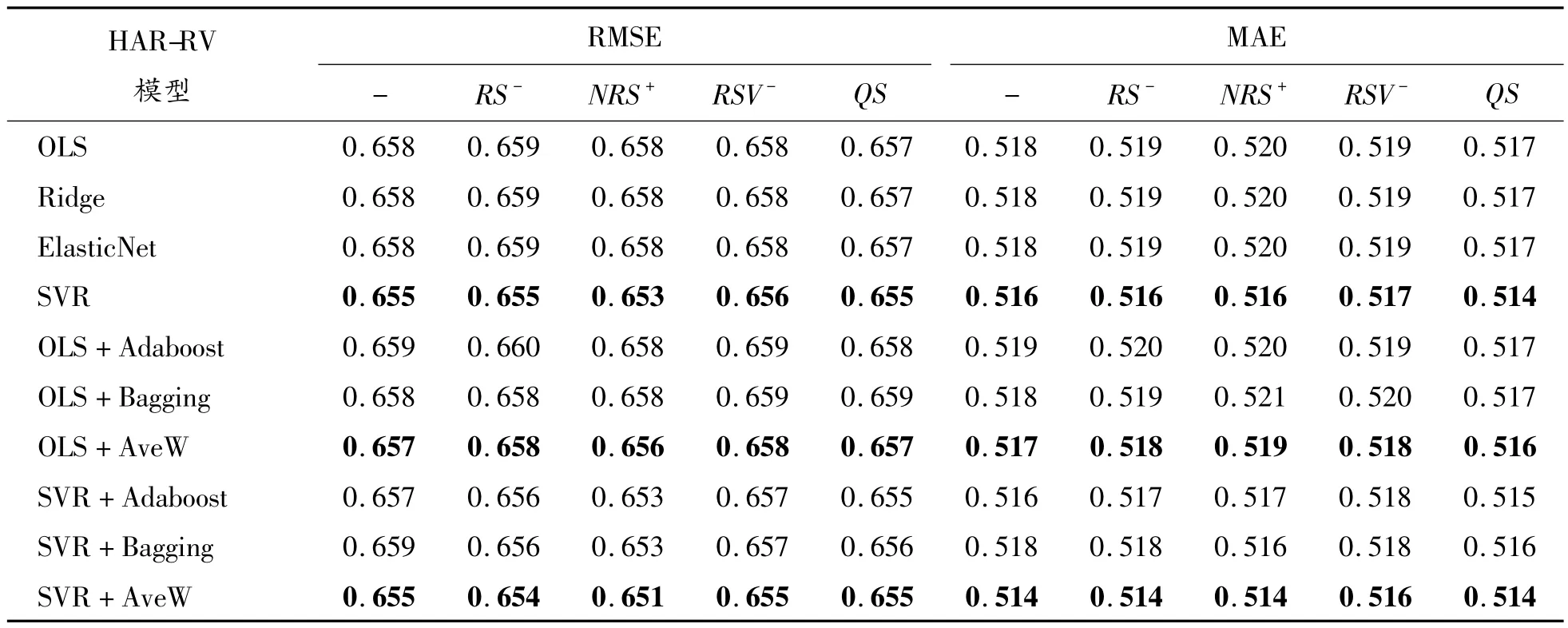
表6 测试集长度比例为50%时不同方法下各个偏度的预测误差

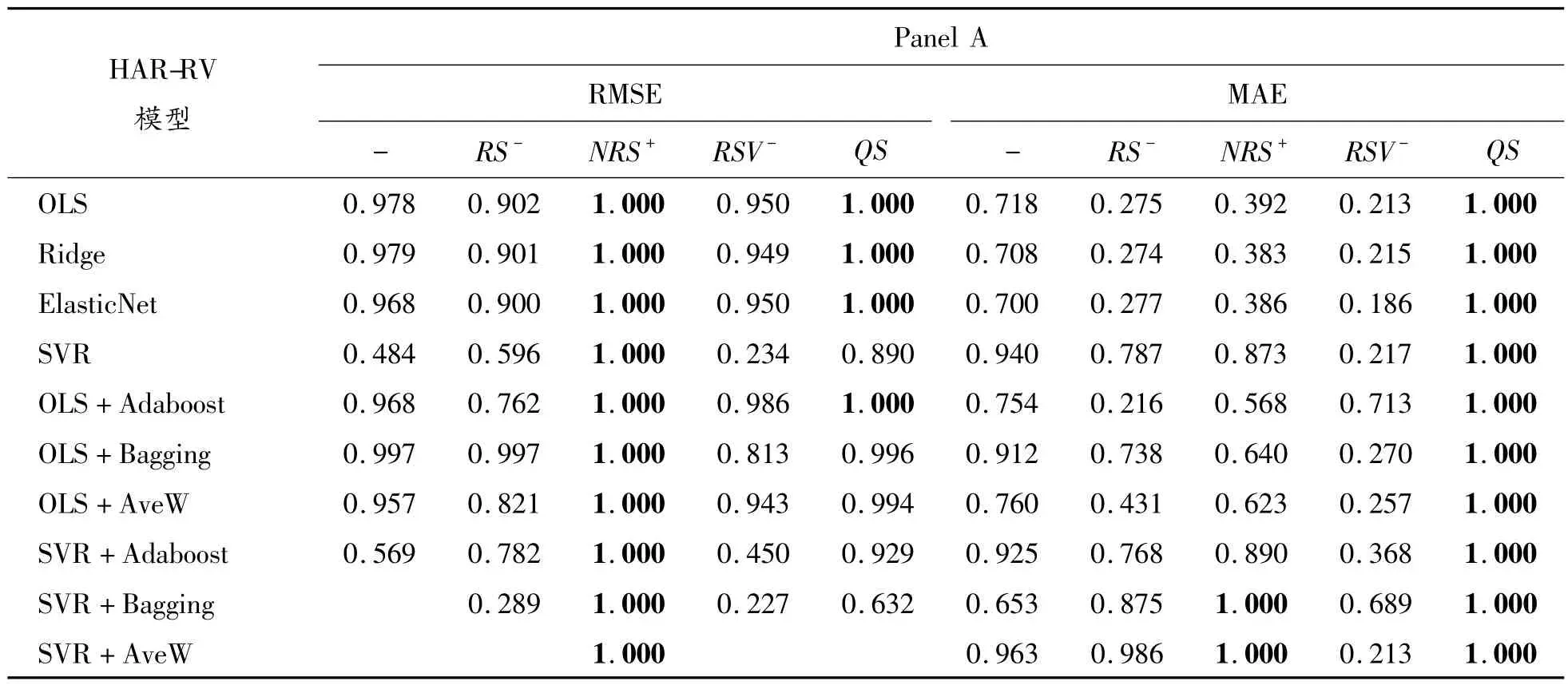
表7 测试集长度比例为50%时两种情况下的MCS 检验结果

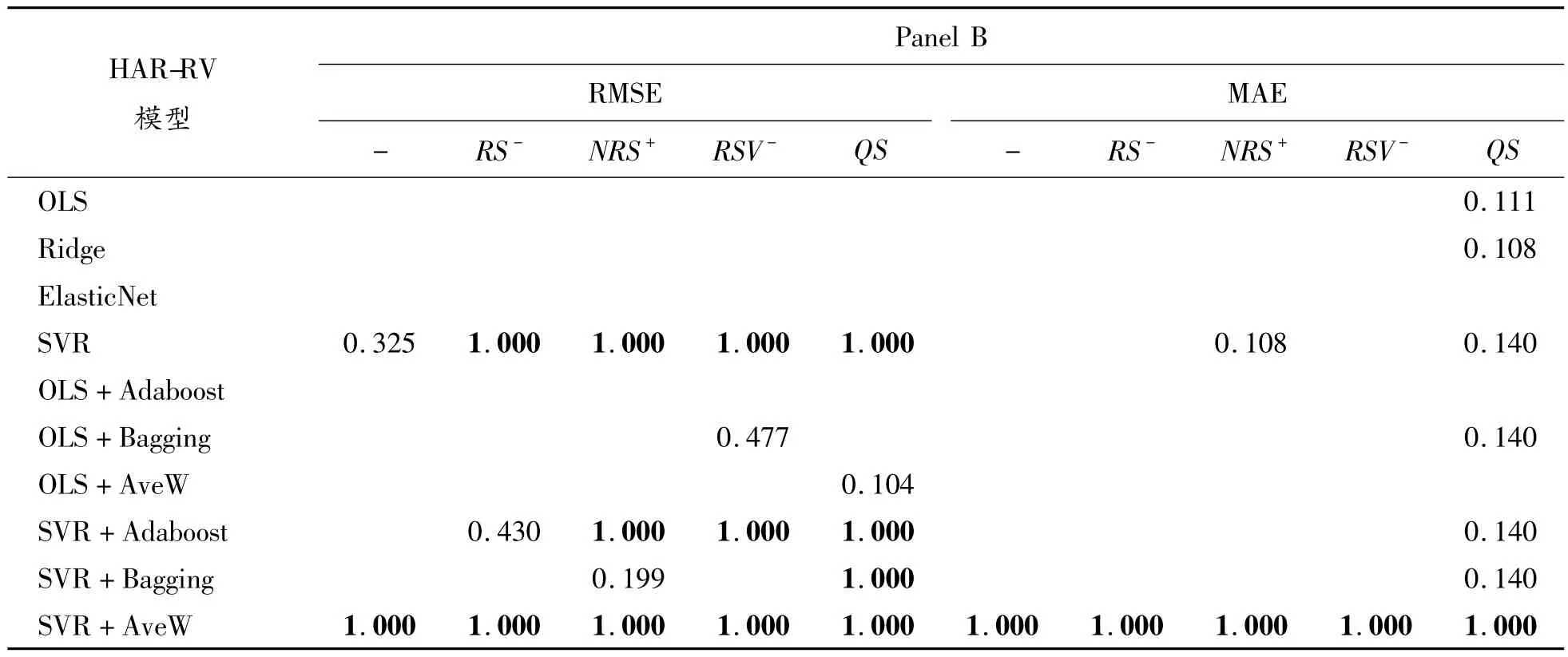
续表(表7)

4 结论

研究了风险中性偏度、基于日数据和日内高频数据的偏度指标所包含的信息差异，通过机器学习方法比较不同偏度对已实现波动的预测能力。经实证发现，随着训练数据的增加，风险中性偏度的预测能力逐渐增强，且优于基于日数据和日内高频数据的偏度指标。在预测方法上，非线性的支持向量回归(SVR)优于普通最小二乘回归(OLS)、岭回归(Ridge)以及弹性网络(Elastic-Net)。在对OLS 和SVR 进行集成学习时，窗口平均预测法能明显改善模型的预测能力，基于SVR的窗口平均预测法的预测能力最强。本文的研究方法和结论对我国金融市场风险管理具有借鉴意义。