基于混合传递路径的摩托车手把振动研究

黄泽好，童 勇，杨峻懿，李晓灵

(1.重庆理工大学 车辆工程学院，重庆 400054;2.力帆科技(集团)股份有限公司，重庆 401122)

0 引言

摩托车手把振动是导致骑手疲劳，影响驾乘舒适性，降低消费者体验的主要原因之一，研究摩托车手把振动舒适性对提升产品竞争力具有重要意义［1-2］。摩托车手把振动是由发动机、路面等多个激励源从不同路径传递至手把处后叠加而成［3］。为此，可同时考虑激励源和传递路径来提升摩托车手把振动舒适性。摩托车行驶时主要受到来自路面和发动机的激励，摩托车手把固有频率一般高于路面最高激励频率，且悬架系统能大幅度衰减路面振动，故发动机为主要激励源［4］。由于摩托车发动机以单缸为主，其振动能量主要通过发动机总成悬置传递，因此需准确识别主要振动传递路径，确定传递特性，为提升摩托车手把振动舒适性提供依据。传递路径分析(transfer path analysis，TPA)方法，是一种基于“激励源—路径—接收者”模型的分析方法，该方法可快速有效追踪摩托车手把振动发生的根本原因。与有限元方法相结合的混合传递路径分析方法(hybrid transfer path analysis，HTPA)，既有传统TPA 方法的高质量，又有有限元方法的灵活性［5-7］。

针对某摩托车发动机激励对手把产生的振动舒适性问题，采用试验与仿真相结合的方式，应用混合传递路径分析方法，识别发动机激励对手把振动影响较大的传递路径，为提升摩托车手把振动舒适性奠定基础。

1 HTPA 模型的建立

试验发现发动机转速6 500 r/min 时手把振动较大。应用加权加速度1/3 倍频程分析，在6.3～400 Hz 范围，手把总加权加速度均方根值为6.68 m/s2，大于标准界限［8］6.30 m/s2，判断手把振动舒适性较差。

为找出导致手把振动的原因，文中采用混合传递路径分析方法。将激励源(发动机)视为主动子系统，把传递路径和“接收者”(手把)视为被动子系统，摩托车发动机主动端一侧与车架被动端一侧的边界处以悬置结构相连接，悬置与车架的连接点为路径点，即振动传递路径的起始点。发动机振动通过悬置结构传递至路径点，随后从路径点在车架上沿不同路径传递至手把处。摩托车振动系统一般是线性时不变系统，各路径传递至手把处的振动的总贡献量为:

式中:Hi(ω)为第i 条路径的结构传递函数;Fi(ω)为第i 路径的工作载荷。

由式(1)可知，手把处的振动总贡献量的确定需要传递函数和载荷两类数据。

发动机总成由左右两侧各3 个悬置与车架连接，每个悬置按照x、y、z 3 个方向传递振动，忽略转动，共18 个路径输入端。以左手把振动为例进行研究，振动方向考虑x、y、z 3 个方向平动，忽略转动，共3 个输出端。各路径以“字母:方向”的形式加以区分。由此，建立的整车振动传递路径模型如图1 所示。

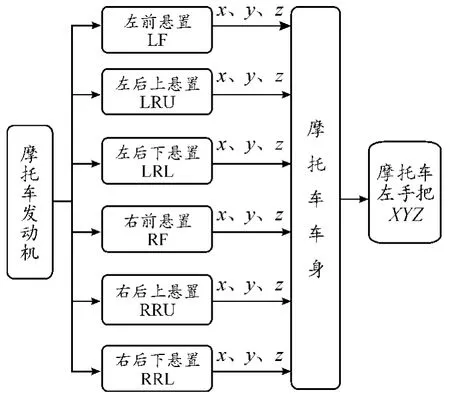
图1 整车传递路径示意图

2 传递函数的获取

传递函数为结构固有特性，是输入位置单位激励力引起的输出位置的响应。获取结构传递函数方法主要有试验法和有限元分析法。有限元法求取模型传递函数，可以避免试验法工作量巨大，实际空间结构狭小难测量，激励源需拆卸等问题［9-10］。

为获取传递函数，建立摩托车整车有限元模型。由于整车有限元模型复杂，模型与实际结构完全一致较为困难，因此，构建主要部件如车架、手把总成、前后减振器总成、后平叉总成、前后脚蹬等有限元模型，适当简化对振动影响较小的部件，例如电池、仪表盘、空滤器、车身覆盖件等，以集中质量代替，然后组集成整车模型

车架有限元模型如图2 所示。单元类型为shell 单元和seam 单元，材料为Q235 钢。车架有限元模型包括92 994 个单元，99 443 个节点。

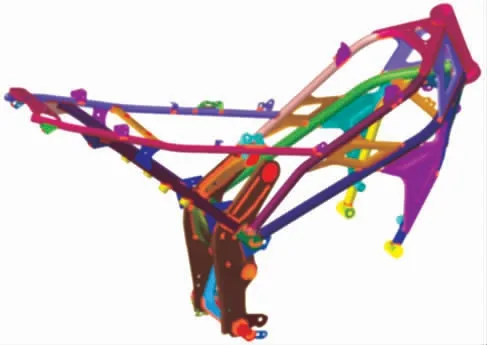
图2 车架有限元模型示意图

通过试验模态分析验证车架有限元模型的可行性，限于篇幅，列出第一阶、第二阶振型，如图3—6 所示。

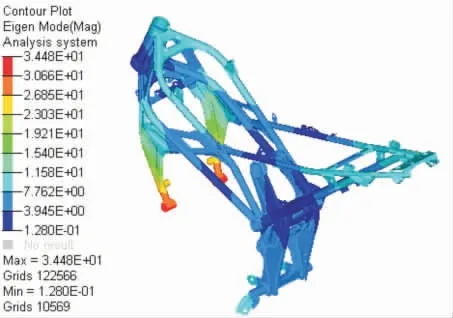
图3 第1 阶计算模态振型示意图

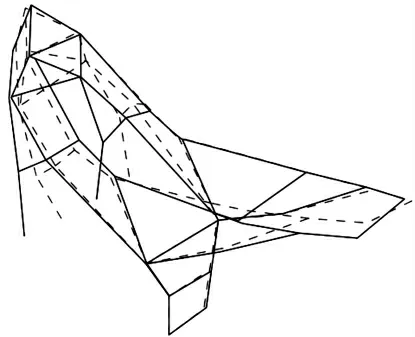
图4 第1 阶试验模态振型示意图

图5 第2 阶计算模态振型示意图

图6 第2 阶试验模态振型示意图

试验模态振型与计算模态振型基本一致，两者模态频率如表1 所示，其误差小于5%，可接受［11］，判断车架有限元模型可行。

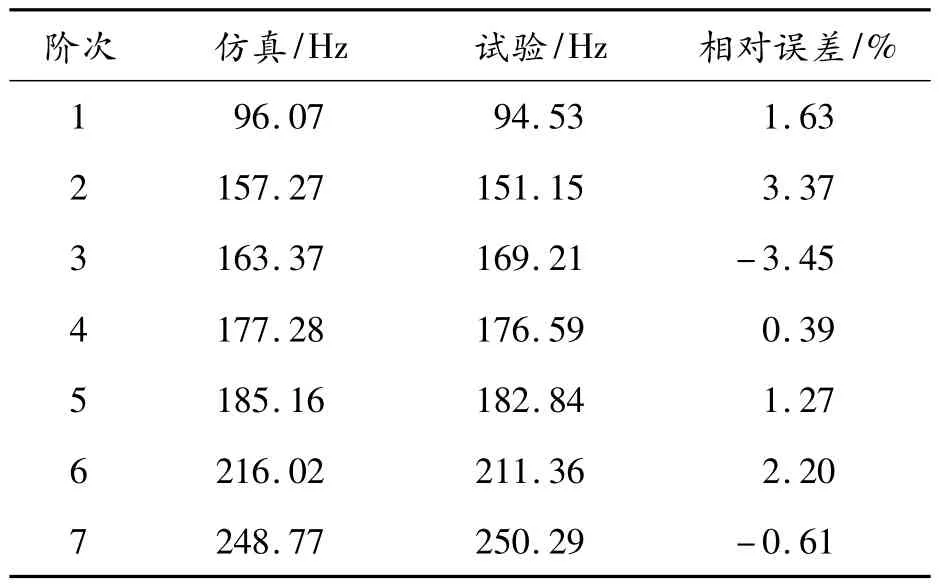
表1 试验与仿真模态

同理，建立手把总成、前后减振器总成、后平叉总成、前后脚蹬等零部件有限元模型。为避免激励力通过发动机作用到其他结构路径上，拆除发动机总成。整车有限元模型如图7 所示。

图7 摩托车整车有限元模型示意图

将Nastran 计算得到的模态文件导入Virtual Lab 中，利用模态叠加法计算出路径点至手把处的结构传递路径，以及用于发动机激励识别的传递函数矩阵。

3 发动机激励的识别

发动机激励一般通过间接方法获得，如悬置动刚度法、单路径求逆法、逆矩阵法以及各种方法混用等［11-12］。摩托车发动机悬置比较简单，为橡胶衬套通过螺栓与车架连接。考虑到悬置动刚度曲线难以获取、结构载荷之间的耦合性以及悬置理论建模的难度，采用逆矩阵法识别发动机激励，为:

式中:am为第m 个指示点的加速度;为指示点之间的逆广义传递函数矩阵;Fn为第n 个路径点的激励力。为获得更多线性无关的方程，以提高激励的识别精度，超定因子取为2［12］，即m=2n。

在指示点，即发动机悬置以及附近各布置一个三向加速度传感器，共12 个，采集发动机转数6 500 r/min 时指示点的加速度数据。为后续验证路径点至手把振动传递函数的可用性，采集左手把的三向振动加速度数据。在Virtual Lab 中计算出指示点之间的广义传递函数矩阵，通过奇异值分解法获得其逆矩阵，根据式(2)识别发动机激励［F］18×1，该车发动机为单缸四冲程，其激励主要表现为往复惯性力的基频、1.5 倍频、2 倍频，而二阶以上的影响很小［5］，故仅考虑300 Hz 内的激励，如图8 和图9 所示(以左前悬置LF激励力为例)。

图8 左前悬置LF 激励力幅值

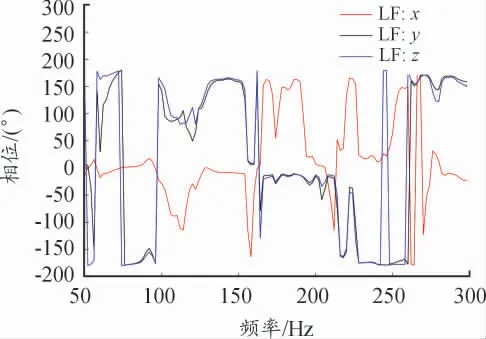
图9 左前悬置LF 激励力相位

4 传递函数的验证

为验证由整车有限元模型得到的传递函数的可用性，用试验载荷仿真得到手把振动加速度，与试验结果进行比较。如图10—12 所示。

图10 左手把x 向振动加速度

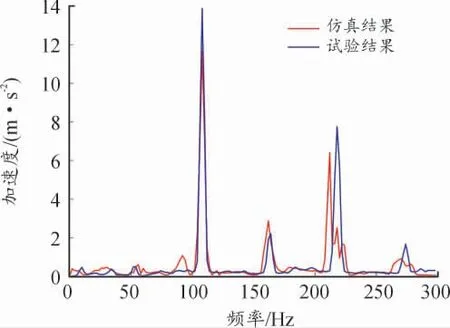
图11 左手把y 向振动加速度

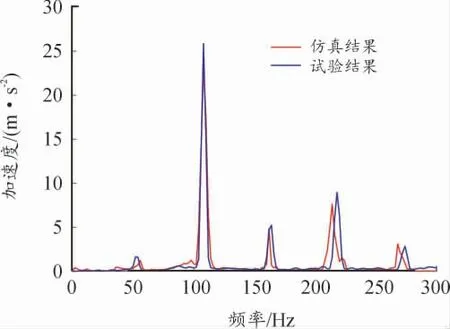
图12 左手把z 向振动加速度

最大峰值频率均为108 Hz、最大加速度幅值误差为15.9%，如表2 所示。仿真与试验结果误差可接受［11］，表明了发动机激励力识别的有效性，同时也证明利用摩托车整车有限元模型计算得到的传递函数可行。

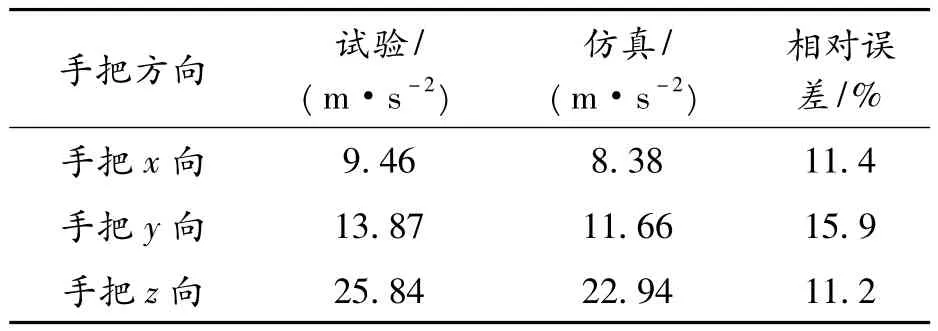
表2 最大峰值

5 振动贡献量分析

由手把三向振动加速度可知，手把在发动机往复惯性力基频(108.3 Hz)激励下振动突出。根据ISO 5349 标准［13］，人体对手把的低频振动更为敏感，故以108.3 Hz 手把振动为例进行分析。应用HTPA，得到各个路径传递至手把处的振动贡献量。考虑各传递路径贡献量存在相位关系而部分抵消，为避免降低或消除某路径贡献量反而增大响应点的振动［14-15］，同时考虑各路径贡献量的相位关系，如图13 所示。

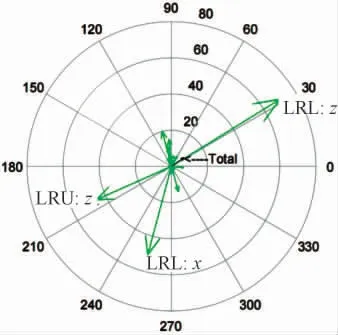
图13 左手把x 向振动贡献量的相位图

各传递路径的综合贡献量为:

式中:Ci为第i 条传递路径的综合贡献量;Ai为第i 条传递路径的贡献量幅值;αi为各传递路径贡献量与总贡献量之间的相角，相角以总贡献量矢量为起始轴，逆时针为正向。

计算各路径点至左手把x 向的综合振动贡献量，如图14 所示。

图14 手把x 向的综合振动贡献量

同理，计算手把y 向和z 向的综合振动贡献量以及相位关系，如图15—18 所示。

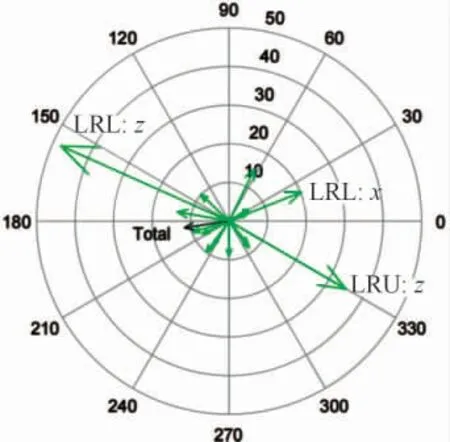
图15 手把y 向振动贡献量的相位图

图16 手把y 向的综合振动贡献量

图17 手把z 向振动贡献量的相位图

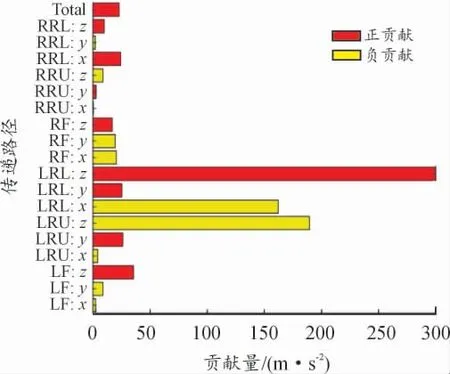
图18 手把z 向的综合振动贡献量

结合振动贡献量以及相位关系，摩托车手把于108.3 Hz 时x、y、z 3 个方向的振动主要由左后上悬置z 向(LRU:z)、左后下悬置x 向(LRL:x)、左后下悬置z 向(LRL:z)贡献。相对于总贡献量，左后下悬置z 向(LRL:z)为正贡献，为增强手把振动;左后下悬置x 向(LRL:x)、左后下悬置z 向(LRL:z)为负贡献，为抑制手把振动。判断手把振动是分别由激励源、振动传递路径，还是二者共同作用所贡献。计算发动机6 500 r/min 各路径点在108.3 Hz 下的激励力以及主要路径的传递函数。如图19—22 所示。

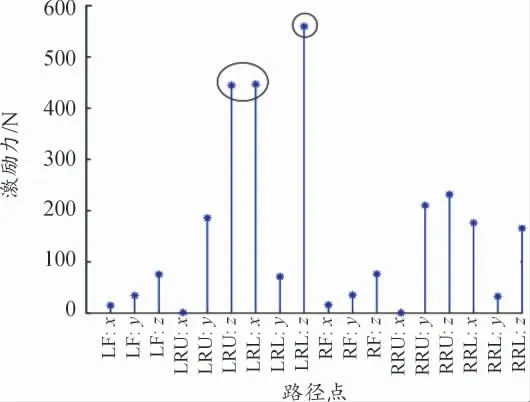
图19 路径点激励力

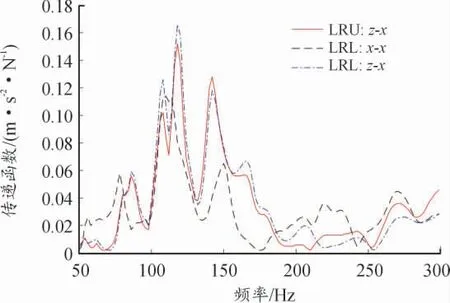
图20 主要路径至手把x 向传递函数

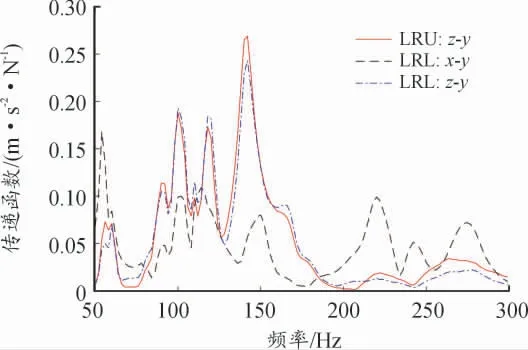
图21 主要路径至手把y 向传递函数

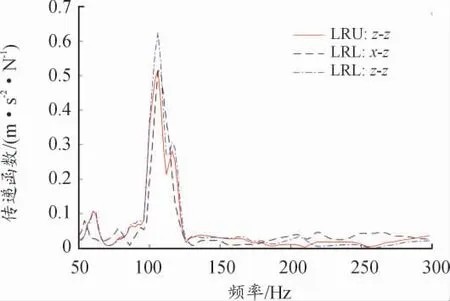
图22 主要路径至手把z 向传递函数

由图13—16 可以得出，主要路径左后上悬置z 向(LRU:z)、左后下悬置x 向(LRL:x)、左后下悬置z 向(LRL:z)的激励力显著，且其至手把3 个方向的传递函数在108.3 Hz 处幅值较大，判断摩托车手把振动超标是激励力与主要路径共同作用导致。考虑左后下悬置z 向(LRL:z)的综合贡献量最大且对手把振动有增强作用，为提升手把振动舒适性，可作对左后下悬置z 向(LRL:z)的隔振性能进行改进，同时也可对手把添加动力吸振器等。

6 结论

建立了摩托车发动机悬置被动端为路径输入点，左手把为输出端的18 个路径输入端和3 个路径输出端的振动传递路径分析模型。利用有限元模态叠加法获取结构传递函数，应用逆矩阵法从台架试验获取的工况数据中提取问题工况的发动机激励。应用混合传递路径分析方法，综合考虑贡献量幅值和相位，识别出导致摩托车左手把振动的主要传递路径，通过激励源与路径传递函数分析，得出手把振动是激励与路径共同作用导致。为降低手把振动提供了工程决策依据。