考虑车尾流动结构的被动减阻方法研究

周海超，陈青云，李慧云，秦润芝

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

0 引言

近年来，随着人们对汽车燃油经济性重视程度的不断提高，如何提高汽车燃油消耗率成为热点研究。有研究发现，当汽车车速达到80 km/h时，汽车行驶过程中75%～80%的阻力来自于气动阻力，而车身前后表面的压差阻力占汽车外部阻力的85%，黏性阻力占比达到15%［1-2］。Ahmed 等［3］提出了模拟汽车尾部构型的简化模型，以研究车尾的流动结构，指出车尾产生的分离区对汽车压差阻力占主要贡献。因此，为了降低空气阻力，研究者针对尾部Ahmed 模型尾部开展了一系列减阻控制方法研究。

气流流经斜面顶边缘和流经垂直面顶边线时发生流动分离，在模型尾部形成涡流尾迹区。国内外学者将合成射流技术、脉冲射流技术等引入Ahmed 模型的主动流动控制研究中，通过给尾流注入能量、改变流动结构达到减阻的目的。Wang等［4］针对25°Ahmed 模型尾部斜面上顶盖设置射流孔，采用合成射流的方法，研究不同射流频率下的减阻效果，发现减阻率最高达13.6%;Krentel 等［5］以25°Ahmed 模型为研究对象，采用闭环脉冲射流方法对其进行减阻控制，最终实现了5.1%的减阻率。张英朝等［6］以35°Ahmed 模型为基础，利用定常射流的方法研究射流孔的位置、速度等因素对尾部流场的影响，实现了最高超过6%的减阻效果。

国内外学者也对Ahmed 模型尾部开展了一系列被动减阻控制方法研究。Wang 等［7］在25°Ahmed 模型尾部安装导流板，并探究不同导流板宽度的减阻效果，发现最高减阻率可达11.8%。Tian 等［8］通过在Ahmed 模型斜背两侧加装襟翼，打破斜背两侧产生的纵向涡，获得最佳减阻21%的效果。郭鹏［9］在35°Ahmed 模型斜背上放置门字型隔板抑制两侧拖曳涡的发展，最终实现了8.39%的减阻效果。Mohammadikalakoo 等［10］通过在Ahmed 模型尾部垂直面增加连接两侧的通道，将气流从高压区吹向低压区来减小尾流，从而降低气动阻力，最高可减少5%的气动阻力。Thacker 等［11］在25°Ahmed 模型顶部与斜背连接处采用圆形边缘连接，防止气流从斜背分离，最终降低了10%的气动阻力。

上述对Ahmed 模型尾部减阻方法的研究中，总体思路是采用不同结构或能量输入来改变尾流结构，最终实现减阻目的，但这些减阻措施在工程实践应用中会一定程度上增加额外的设计成本或受加工条件的限制。由于Ahmed 模型斜背与车顶和尾部后垂直面相接触的边缘是锐利的直线，气流流经35°Ahmed 模型尾部时发生完全分离，故可通过改变斜背与车顶以及尾部垂直面的连接方式，抑制车体尾部的分离，进而改变车尾流场结构以起到减阻的作用。因此，选择35°Ahmed 模型为对象，对车体背面尾部边线进行圆滑过渡处理以推迟流动分离，进而探究不同边线圆角半径对尾流结构和流动阻力的影响，最终确定改善的最佳过渡半径。

1 仿真方案设置及模型验证

1.1 CAD 模型

Ahmed 模型由钝形前端、尾部斜面和垂直面以及4 根立柱组成，由于结构简单，能有效捕捉车尾周围流场结构而被广泛研究。以35°Ahmed 模型为基础，对车尾斜面顶端边线a 与车尾斜面底部边线b 进行圆滑过渡处理，从而抑制尾部流动分离，改善尾流结构，最终达到减阻效果。a、b 两边线位置如图1 所示。

图1 a、b 两斜边位置示意图

Ahmed 模型长1 044 mm，宽389 mm，高288 mm，距地面高50 mm，同步设定边线a 和b 的过渡圆角半径分别为0、25、50、75、100 mm。汽车模型几何参数如图2 所示。根据不同的圆角半径，将所有的模型分为5 个方案。本文中所有三维建模工作均在三维软件-Solidworks2019 中完成。

图2 汽车模型几何参数示意图

1.2 计算域及边界条件设置

所有模型被放置在一个长方体计算域中。为了排除地面效应对数值计算结果的影响，模型前端距离计算域入口为车身长L 的1.5 倍，后端距离计算域出口为车身长L 的5.5 倍，计算域宽度为模型宽W 的7 倍，计算域高为模型高H 的4 倍，计算域的长×宽×高分别为8.352 m×2.723 m×1.352 m，阻塞比为3.1%，满足计算要求。计算域尺寸如图3 所示。计算边界条件见表1。

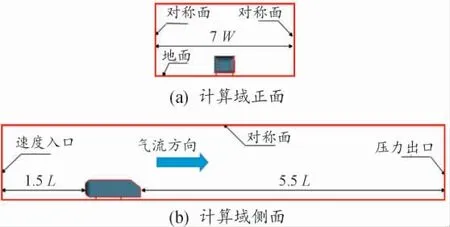
图3 计算域尺寸示意图

表1 边界条件

1.3 数值模拟方法

数值计算均基于商用CFD 软件STAR-CCM+15.02。DES 方法是RANS-LES 混合方法，在近壁面区域以及湍流长度尺度小于最大网格尺寸的区域采用RANS 方法求解，当湍流长度尺度超过网格尺寸时，区域使用LES 方法求解。此方法能保证较高的计算精度，有效减少计算量，因此采用DES 方法进行计算。采用的IDDES 模型的控制方程为:

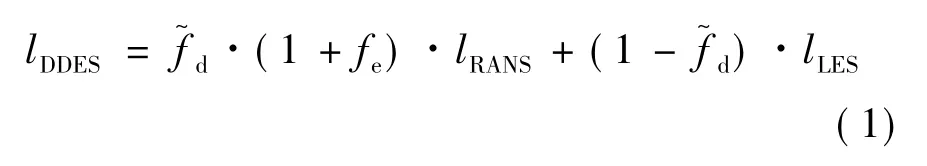
计算过程分为定常计算和非定常计算。定常计算采用SST K-omega 模型对模型进行定常求解，迭代4 000 步后满足收敛残差0.000 1;之后将定常计算结果作为非定常计算的初始流场。非定常计算采用SIMLEC 算法耦合压力与速度场，离散格式为二阶迎风格式，计算时间步长为1×10-3s，单位时间步内迭代5 次，非定常计算时长为2 s，总计算时间步为10 000 步。

1.4 网格生成及验证

为节省计算资源，保证数值计算有较高的精度，采用STAR-CCM+自带的多面体网格生成器生成的多面体网格。汽车近壁面受到气流黏性作用的影响，分为黏性底层、过渡层和对数层。为确保车身近壁面流动处于黏性底层，引入量纲为一参数Y+评价第1 层网格高度，其定义为［12］:

其中:ρ 为气流密度;μτ为壁面摩擦速度;y 为边界层厚度;μ 为气流速度。一般认为，当Y+＜5时，流动处于黏性底层，即第1 层网格高度满足DES 方法对数值计算的要求。本文中设计了一套网格方案以满足湍流模型对Y+值的要求，模型网格划分情况见表2。

为确保数值模拟结果的可靠性，在表2 参数设定范围内，基于初始的35°Ahmed 模型分别设置了粗网格、中等网格和细网格等3 套方案，不同方案的仿真结果与Meile 等［13］的试验结果见表3。从表3 中可以看出，随着网格不断加密，仿真精度不断逼近试验值，细网格方案Cd 值与试验值仅有0.7%的误差。

表2 模型网格划分

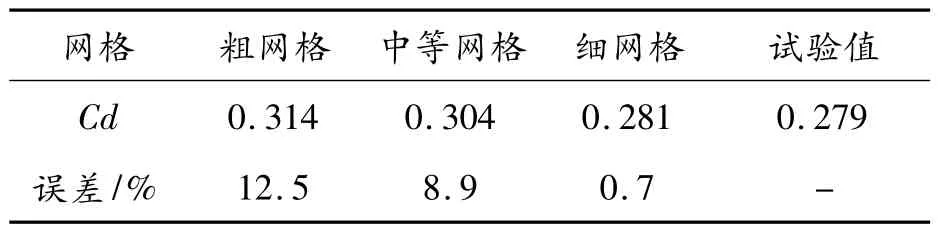
表3 不同网格的仿真结果

图4 反映了仿真与试验在对称平面上的流向速度分布，其速度分布有较好的一致性。因此，采用细网格方案为所有数值计算模型加密。图5 显示了细网格划分方案下Y=0 对称面上的网格结构。图6 是模型外壁面Y+值云图，整体Y+值符合计算要求。

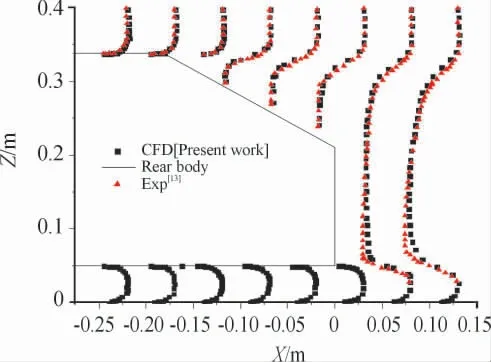
图4 流向速度曲线

图5 初始35°Ahmed 模型网格示意图

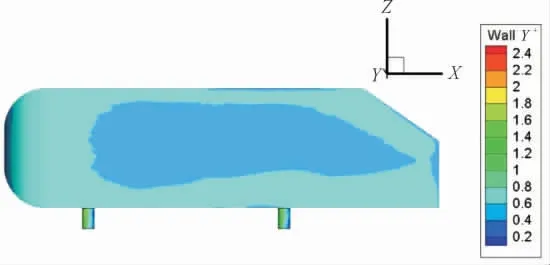
图6 壁面Y+云图(以初始35°Ahmed 模型为例)

为确保上述模拟方法的精确性，对尾部倾角分别为0°和25°的Ahmed 模型采用上述同样的模拟方法进行计算，计算结果与Ahmed 等［3］试验结果如表4 所示。可以看出，在不同尾部倾角下，仿真值与试验值的误差较小，证明本文的仿真计算方法是精确可靠的。

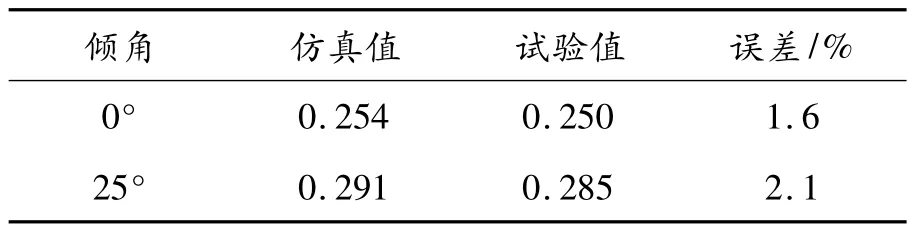
表4 不同倾角下的阻力系数

2 仿真结果分析

基于上述细网格划分方案，表5 列出了不同圆角过渡参数下的空气阻力系数，以及相对于初始35°Ahmed 模型计算空气阻力系数的减阻率。从表5 中可以看出，对斜面边线进行过渡处理能有效降低空气阻力系数，最大降幅为6.4%。

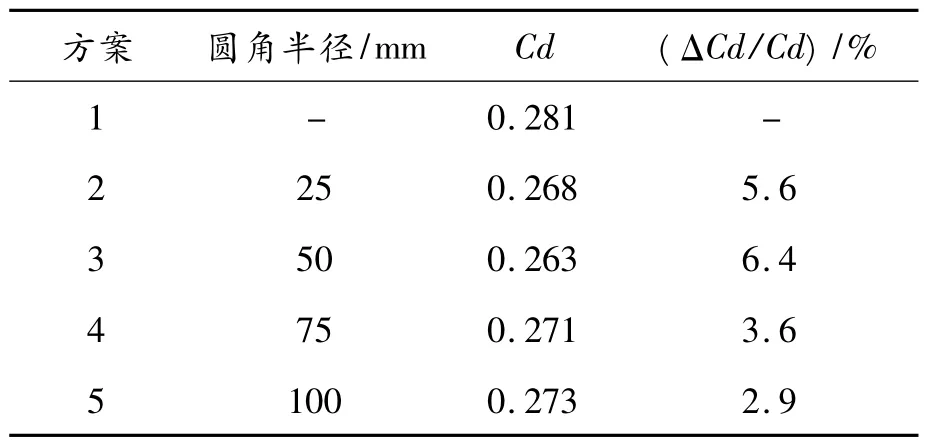
表5 不同圆角半径下的减阻率

2.1 尾流瞬态速度分布

通过对比对称平面内沿气流流向的速度分布得到不同方案下尾流速度的变化，如图7 所示。气流从斜背上方分离，一部分气流从斜背上方向下游流动，与车底的上卷气流在尾部垂直面后相互作用，形成尾部回流区，导致尾部压力降低，带来较大的气动阻力。从图7(b)—(c)可见，适当增大过渡圆角半径，沿斜背下洗气流增多，缩小了斜背中下方回流区的面积，抑制了此处的流动分离;而在图7(d)中，圆角与斜背过渡不够平顺，导致气流在两者连接处再次出现明显的流动分离现象;在图7(e)中，继续增大过渡圆角半径，实现了圆角与斜背的平滑连接，最终回流区继续收缩。应注意到的是，过渡圆角半径对尾流速度分布有着重要贡献。总地来说，对边线a 和b 采用圆角过渡后，沿斜面下洗气流明显增多，提高了尾流的速度梯度，这表明沿斜面下洗气流对降低尾流的能量耗散、增强尾流的稳定性具有积极意义。

图7 对称平面内尾部气流流向速度等值线图

2.2 尾部压力系数分布

气流流经模型尾部产生的流动分离影响了尾部表面压力系数分布，这是造成模型前后产生压差阻力的重要因素。模型尾部表面压力直接关系到整车模型的压差阻力，各模型尾部表面压力系数分布如图8 所示。从图8(b)—(c)中可以看到，随着过渡圆角半径的增大，进入斜面的气流增多，斜面两侧拖曳涡在斜面上诱导出较大的低压区;同时提高了斜背上方气流的动能，增强了斜面边界层抗逆压梯度的能力，提升了斜背表面和垂直面的压力，尾部表面静压总体回升，整车气动阻力系数由此降低。相反，在图8(d)中，由于进入斜面的气流减少，斜面顶部及两侧压力回升，但斜面底部与垂直面处回流区扩大，导致斜面底部与垂直面处的压力明显降低，气动阻力系数开始回升。在图8(e)中，进入斜面上方的气流开始增多，斜面顶部以及两侧的低压区域明显扩大;而斜面与垂直面接合区域上方的气流动能增加，抑制了边界层的流动分离，导致这一区域压力有一定上升，尾部压力总体降低，这就是圆角半径超过50 mm后气动阻力系数迅速回升的原因。

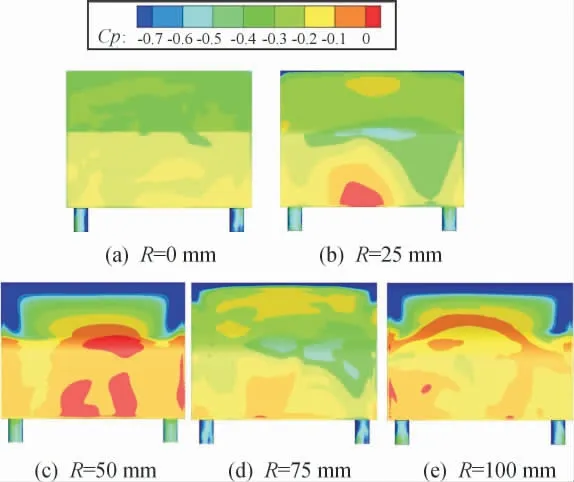
图8 尾部表面压力系数分布云图

2.3 尾部涡量分布

图9 是Ahmed 模型在Y=0 对称面内涡量分布云图。从图9(a)可以看到，初始Ahmed 模型尾部流动结构主要由一对反向旋转的涡N1、N2以及由N1诱导产生的分离泡组成。气流流经模型顶部以及尾部垂直面底边时，在模型顶部和底部产生了2 个涡量集中区，其中顶部涡量区所占空间较大，对斜面和垂直面后部流动影响较大。尾部产生的分离涡沿来流方向向后输运，改变了尾部涡量分布，最终影响尾流的流动稳定性。

从图9(b)—(c)可以看出，对模型尾部采用圆角连接方式后，沿圆角进入斜面上方的气流随着圆角半径的增大而增多，涡N2尺度有一定减小并且向后推移，涡N1尺度明显减小且逐步向尾部垂直面靠近，受到涡N2诱导产生的逐渐分离泡消失。这对模型尾部斜面下端以及垂直面的表面压力回升起到积极作用，与图8(b)—(c)的结果相符合。同时，尾部斜面上方的涡量明显减少且向斜面倾斜，沿斜面下洗气流的增多也加强了与流经车底气流的相互作用，使模型底部涡量缓慢上升。总地来说，逐步增大圆角半径能有效抑制尾部的流动分离，尤其是斜面顶部的分离，减少了尾流能量耗散，有利于降低尾流的不稳定性。

从图9(d)中，一部分气流在圆角和斜面接触处发生分离，导致沿斜面下洗气流减少，模型尾部再次形成较大的回流区，此时涡N1尺度明显增大且位置明显上移，并诱导了斜面边界层分离产生分离泡，导致斜面表面压力有一定下降，这对整车的气动阻力系数上升有一定的影响。另外，这也导致斜背上涡量有所增长并且逐渐远离斜背。由于较少的气流进入回流区与车底气流掺混，导致涡N2消失，尾部垂直面后的涡量有所降低。

在图9(e)中可以看到，圆角与斜面的平稳过渡将一部分气流引入斜面上方，尾部回流区明显缩小，涡N1的尺度随之减小，斜背上方的涡量相对图9(d)有一定减小。此外，从斜面下洗气流与车底气流混合形成涡N2，增强了垂直面后的涡量。涡N1的削弱表明斜面与垂直面接合区域压力有一定上升，而涡N2的重新出现意味着相应区域压力降低，这与图8(d)—(e)中的结果一致。

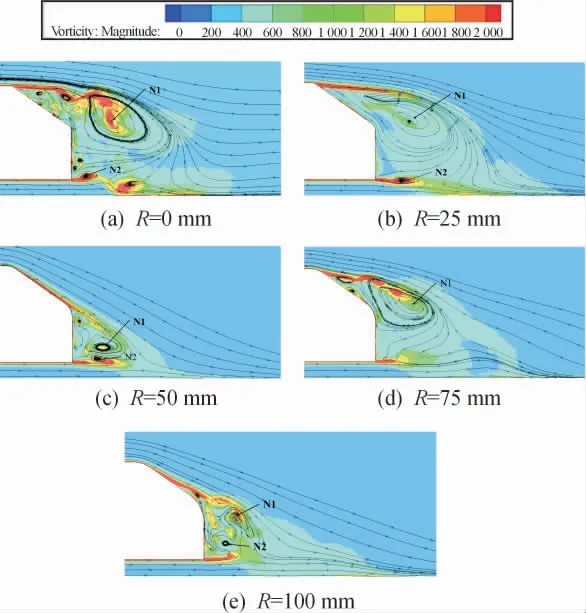
图9 对称面内尾部涡量分布云图

2.4 尾部涡系结构分布

Q 准则由Jcr 等［14］提出，定义如下:

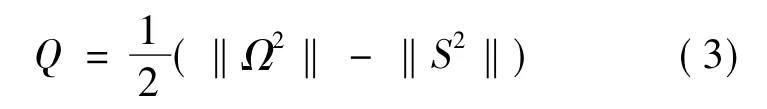
式中:Ω 为旋转张量;S 为应变张量。当Q＞0 时，表示旋转程度大于变形程度，认为此处存在漩涡。Q 准则通过影响剪切层来有效识别流体运动的涡结构，本文中采用Q 准则识别Ahmed 模型尾部空间涡系结构。

不同方案的Ahmed 模型尾部涡系结构如图10 所示。Ahmed 模型尾部涡系结构主要由3 个部分组成，即尾部斜面上的分离泡、斜面顶部两侧的拖曳涡、尾部垂直面底端的回流区［15］。从图10(a)—(c)中可以看到，由于尾部斜面过渡圆角半径增大，在沿斜面上方向下流动的气流以及侧边气流的卷吸作用下，斜面顶端两侧剪切层卷起形成的拖曳涡逐渐伸长，增强了尾流能量的耗散，但也抑制了斜背上分离泡的产生及回流区的流动分离，气动阻力系数随之明显降低。在图10(d)中，由于沿圆角进入斜面上方的气流减少，斜面两侧拖曳涡强度有所减弱，在壁面黏性作用下斜面中下部抗逆压梯度能力下降，斜面上产生较多的分离涡，提高了模型的气动阻力系数。从图10(e)中可以看出，过渡圆角半径持续增大，斜面两侧拖曳涡增强，抑制了斜背表面边界层的分离，同时加强了与斜面底部气流的掺混，这是导致垂直面后方横向涡增多和气动阻力继续升高的原因。

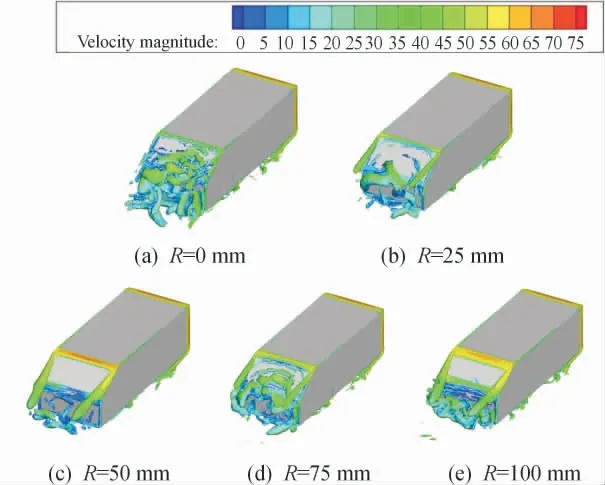
图10 Q 准则等值面(Q=15 000)下不同方案的模型尾部涡系结构图

3 结论

1)尾部圆角半径从0 mm 增加到50 mm 时，改善了尾流结构，有效提升了模型尾部的表面压力，减少了模型的压差阻力，最终实现了较好的减阻效果;当圆角半径继续增大至75 mm 和100 mm时，斜面顶部两侧表面压力持续降低，最终导致尾部总体的表面压力降低，减阻效果逐渐变差。

2)尾部斜面两侧卷起的拖曳涡直接影响尾部流动形态。适当增加圆角的半径能延长拖曳涡的强度，减小斜面后方涡N1和涡N2的尺度，并抑制由涡N1诱导产生的分离泡，减少尾流的能量耗散，提高尾流的流动稳定性，达到改善尾流结构、降低气动阻力的目的。