基于P-NAEKF 算法的汽车行驶状态估计
2022-05-18戴凌宇冯张棋马成宇胡子添
戴凌宇,冯张棋,马成宇,胡子添
(1.南通大学 电气工程学院,江苏 南通 216000;2.江苏大学 汽车与交通工程学院,江苏 镇江 212013;3.江苏大学 汽车工程研究院,江苏 镇江 212013)
0 引言
近年来,自动驾驶技术飞速发展,其安全性被社会广泛关注。随着自动驾驶技术离开实验室走向社会,将面临更加复杂的交通状况,为了确保车辆自身的安全性,它需要准确感知面临的环境并做出合理决策[1]。目前很多高精度的传感器因为产品价格问题不能普及到所有的汽车,有些关键状态参数难以直接量测,所以需要使用一些较为廉价的传感器先获取一部分状态信息,利用这些信息对不宜直接测量的关键车辆状态进行估计,有效保障汽车安全自动驾驶[2]。
目前针对汽车的状态估计的方法主要有:扩展卡尔曼滤波、无迹卡尔曼滤波、容积卡尔曼滤波、粒子滤波、滑模观测器和神经网络的方法[3-8]。赵强等[9]考虑车辆侧向运动、横摆运动和侧倾运动,建立非线性模型,设计了扩展Kalman滤波器来过滤噪声追踪实际值;方贤生等[10]将模糊控制引入到无迹卡尔曼滤波算法中,提出了一种模糊自适应无迹卡尔曼滤波算法完成车辆状态参数估计;邢德鑫等[11]针对车辆状态估计中的强非线性、噪声非高斯问题设计了一种自适应容积粒子滤波状态估计器。以Kalman 滤波理论为基础的车辆状态估计方法是当前研究的主流方向[12]。
郝亮等[13]基于3 自由度的车辆模型采用标准的扩展卡尔曼滤波(EKF)方法对横摆角速度和质心侧偏角进行了估计,仿真验证了其有效性,但其噪声特性是通过试验和经验得到的,难以验证其准确性,影响了滤波效果;Li 等[14]提出了基于多种传感器信息融合的EKF 汽车状态估计方法,虽然考虑了多种噪声特性集合,但本质上还是假设噪声统计特性已知,适用范围有限;李静等[15]提出了一种自适应容积卡尔曼滤波,它是将标准的容积卡尔曼滤波(cubature kalman filter,CKF)与Sage-Husa 次优估计算法结合在一起,对部分车辆参数实时在线估计,虽然该方法解决了噪声协方差的估计问题,但是Sage-Husa 次优估计方法容易使噪声协方差失去正定性而导致滤波发散。
根据上述讨论,以往对于EKF 在车辆状态估计的研究中,在噪声协方差的不准确性问题上还存在一些不足,为了改善这一问题,本文分析了噪声协方差不准确给状态估计结果带来的影响,给出了2 种噪声协方差的估计方法:基于Sage-Husa的次优估计方法和基于粒子群的噪声协方差优化估计方法,分析了Sage-Husa 次优估计算法容易发散和过于依赖统计特性的不足,选择粒子群算法对不精准的噪声协方差进行优化估计,并将这一部分作为参数估计模块与传统EKF 算法相结合,提出噪声自适应的EKF 算法(P-NAEKF),该算法能在噪声协方差不准确时对其进行估计修正,大大提高了滤波精度,经过仿真验证,这种算法能够完成车辆行驶状态的准确估计。
1 3 自由度车辆模型
1.1 模型构建
构建基于纵向车速,横摆角速度和质心侧偏角的3 自由度模型[13]如图1 所示。
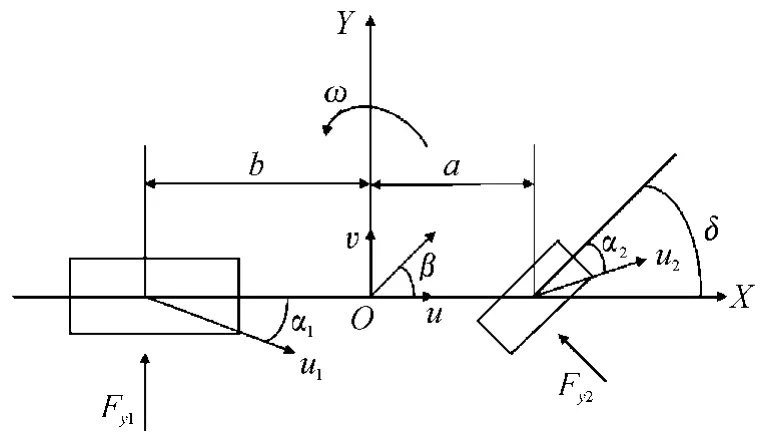
图1 3 自由度非线性模型示意图
图1 中,XOY 是以车辆质心为原点的坐标系,其中:X 轴与车辆的纵向对称轴重叠,并且选择向右为正方向;Y 轴通过车辆的质心,并选择向上为正向。选择质心侧偏角,横摆角速度和纵向速度为状态量,选择纵向加速度为量测量,选择横向加速度和方向盘转角为控制量构建如下的3 自由度非线性汽车状态方程:

式中:β 为车辆质心侧偏角;ω 为车辆横摆角速度;u 为车辆纵向速度;ax为车辆纵向加速度;ay为车辆侧向加速度;δ 是车辆的前轮转角。
1.2 模型转换
使用扩展Kalman 滤波算法对式(1)进行状态估计,假设u 在采样周期T=0.01 s 内不变,将汽车状态方程离散化:

将式(1)与式(3)联立方程组并移项可得
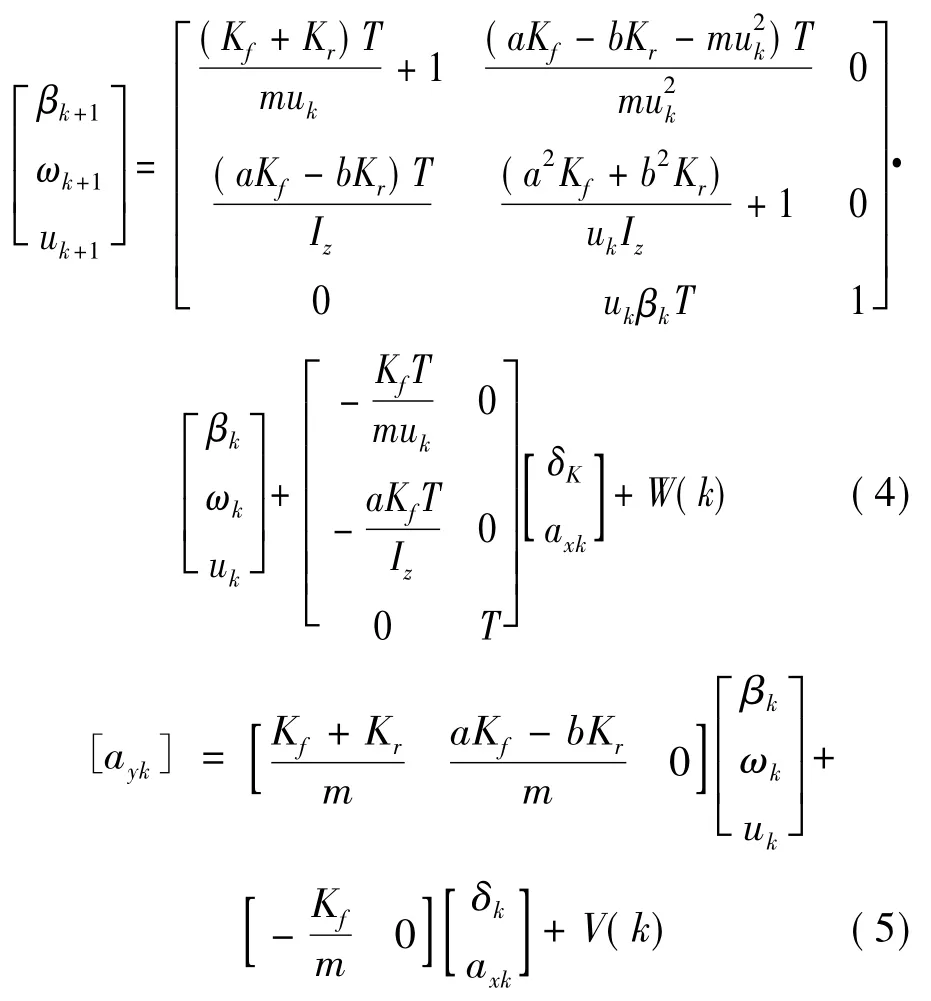
式中,相关参数值如表1 所示。

表1 车辆参数
2 传统EKF 算法及问题描述
2.1 传统EKF 算法
基于式(3)和式(4)可知状态方程和量测方程可以表示为:

式中,状态变量x=[β,ω,u]T,输出变量z=[ay]T,控制变量u=[δ,ax],wk-1与vk为互不相关的高斯白噪声,且服从正态分布。
传统的EKF 用于汽车状态估计时,噪声协方差R 和过程噪声协方差Q 往往是通过不断调试或是经验得到的[16],此时可以得到EKF 的迭代方程:

式中:A 和H 是通过求取状态x 的雅可比矩阵得到的,将式(4)和式(5)展开可得式(13)和式(14),再依据式(15)和式(16)求解得到A 和H。

2.2 性能匹配分析
在实际汽车状态估计时,复杂的路况环境是千变万化的,传感器受到干扰往往会导致噪声协方差存在误差,对滤波性能的干扰是极其巨大的[16]。当系统存在不匹配的噪声方差,可以得到:
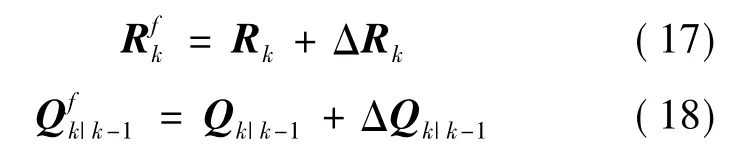
式中:Rk表示真实的量测噪声协方差;Qk|k-1表示真实的过程噪声协方差;上标f 表示实际应用假设值;ΔRk和ΔQk|k-1表示实际应用假设值和真实值的偏差。
在滤波过程中,通常用估计误差协方差来表示滤波估计的均方误差(mean squared error,MSE),根据不准确的噪声方差和乘性噪声相关系数,得到不准确的均方误差(FMSE)为:

其中
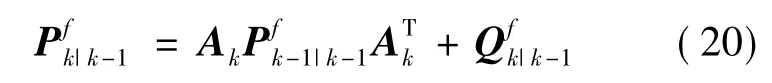
式中,上标f 表示滤波器实际的计算值,但是这个计算值与真实值存在一定的偏差,所以并不是真实的MSE。真实的均方误差(TMSE)为:
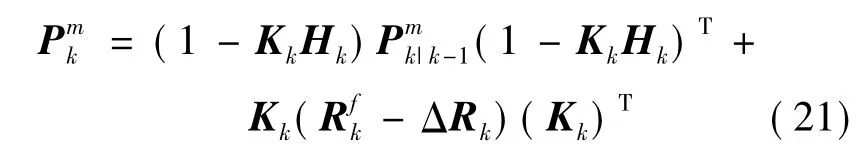
其中

对比式(19)和式(21)可以发现,当噪声协方差存在误差时,仍然使用不精准的噪声协方差来设计Kalman 滤波器,将会导致估计误差协方差与真实的TMSE 存在偏差,Kalman 滤波器的精度降低,因此有必要设计一种噪声自适应滤波算法解决噪声协方差不精准的问题。
3 2 种参数优化估计方法
3.1 基于Sage-Husa 的噪声协方差估计方法
Sage-Husa 算法[17]是一种利用协方差特性估计噪声协方差的方法,该方法已得到证明,现作简要描述:
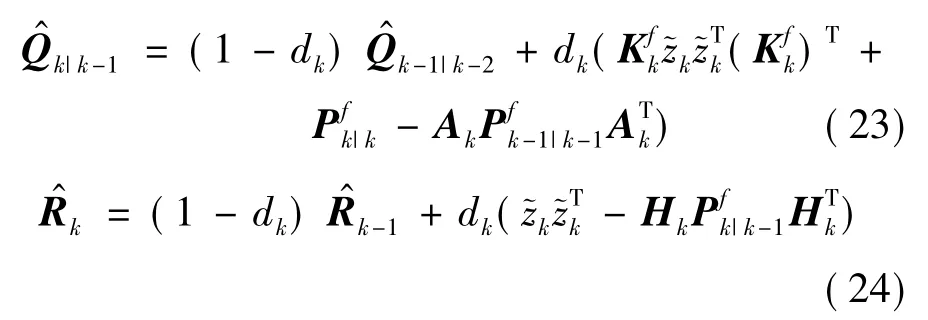
式中,dk=(1-c)/(1-ck+1),0<c<1 为遗忘因子。
但是直接使用这种算法估计噪声协方差存在一些问题:
1)式(23)和式(24)中运用了减法运算,虽然能够满足无偏估计的要求,但容易使得噪声协方差失去正定性导致滤波发散。
2)过于依赖噪声统计特性,估计效果取决于信息的好坏。
3.2 基于粒子群算法的噪声协方差估计方法
3.1 节中介绍了基于Sage-Husa 的噪声协方差估计方法,但存在一些问题,于是本小节以汽车状态估计扩展Kalman 滤波器为研究对象,针对过程噪声协方差和量测噪声协方差不精准的情况,提出一种新的估计方法即粒子群算法估计噪声协方差。
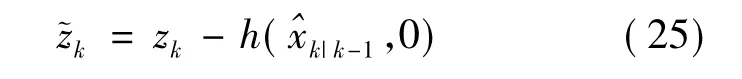
新息协方差的计算值为:
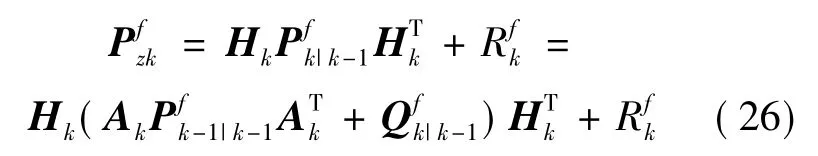
新息协方差的实际值为:

根据式(23)式(24)可以得到:

为了保证ΔRk和ΔQk|k-1尽可能小,设置适应度函数:
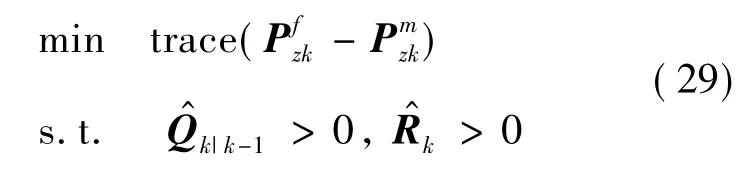
在每次迭代后,产生一组最优值,即个体最优值(gbest)和全局最优值(pbest),粒子通过最优值更新位置和速度,即:
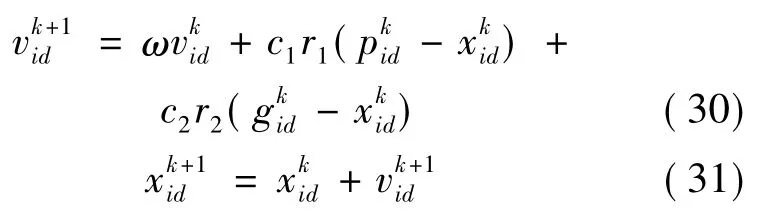
通过迭代寻优得到适应度最小的粒子位置b=(b1,b2,…,bD)T,即得到噪声协方差的估计值:

该算法与3.1 节提出的传统Sage-Husa 方法相比,保证了正定,提高了算法的收敛性。
参数估计算法流程图2 所示。
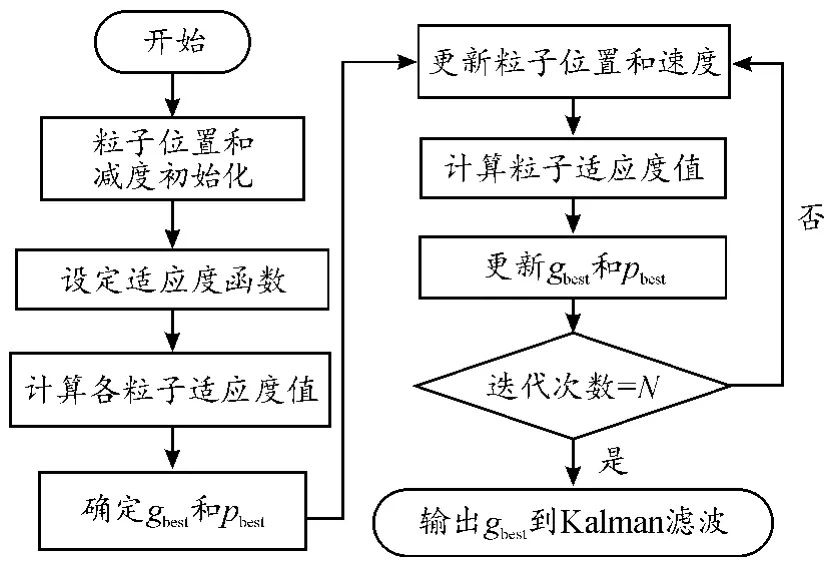
图2 噪声协方差估计算法流程图
4 P-NAEKF 算法
基于3.2 节的参数估计方法,可以得到较为准确的噪声协方差的值,将这种参数估计方法嵌入传统的EKF 算法中,可以得到P-NAEKF 算法。
P-NAEKF 算法流程如表2 所示。

表2 P-NAEKF 算法流程
5 仿真分析
5.1 Carsim 与Matlab/Simulink 联合仿真平台
在本文中,首先在Carsim 中搭建车辆模型,并设定工况[18],将其与Matlab/Simulink 中建立的传统的EKF 算法模块与本文的P-NAEKF 算法模块联合仿真,对汽车的纵向车速、横摆角速度和质心侧偏角等相关参数进行实时估计,并对比估计结果,验证P-NAEKF 算法的优越性。
联合仿真平台如图3 所示。

图3 Carsim 与Matlab/Simulink 联合仿真平台框图
工况设定:选取Carsim 中自带的双移线工况,路面附着系数为0.855,其他车辆参数见表1 所示,准确的噪声参数为:
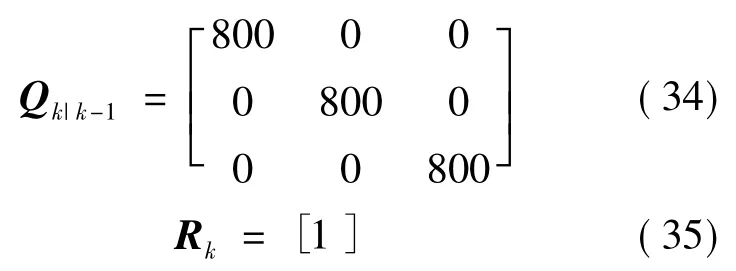
将传感器测量的纵向加速度、侧向加速度以及方向盘转角信号作为估计模块输入信号,3 个输入信号如图4—6 所示。

图4 侧向加速度输入信号

图6 方向盘转角输入信号
5.2 参数估计
本章节使用2 种参数估计方法对噪声协方差进行估计,进行50 次蒙特卡洛实验,并对估计效果进行比较,结果如图7 所示。
方法1:传统的Sage-Husa 算法,对应文中3.1节提出的方法;
方法2:基于粒子群算法的参数优化估计方法,对应文中3.2 节提出的方法。
这一部分对过程噪声协方差进行了估计,比较2 种不同的估计方法,观察图7 可以清晰地发现,方法2 的估计效果明显好于方法1,且50 次的结果均稳定在真实值附近,误差在0~±2.5 之间,仿真表明方法2 能够较好地估计过程噪声协方差。

图7 过程噪声协方差估计结果
这一部分对量测噪声协方差进行了估计,使用了方法1 和方法2 并做了比较,从图8 可以清晰地发现,方法2 的估计效果明显好于方法1,且50次的估计结果稳定在真实值附近,误差在0~0.02之间,仿真表明方法2 能够较好地估计量测噪声协方差。

图8 量测噪声协方差估计结果
综上所述,本文提出的参数优化估计方法可以在噪声协方差不准确情况上估计出准确的噪声协方差,为车辆状态估计提供保障。
5.3 汽车状态估计
为了便于描述,现对状态估计算法做如下简化定义:
算法1:传统的EKF 算法即2.1 节介绍的算法,其中噪声协方差使用不准确的固定值:


算法2:本文提出的P-NAEKF 算法,对应第4章提出的算法,其中已知不精准的噪声协方差与算法1 设置一样,实际算法采用的噪声协方差通过5.1 节的方法2 估计得到。
通过传统EKF 算法估计的纵向车速以及本文提出的P-NAEKF 算法估计的纵向车速与Carsim输出参数值进行对比分析。纵向车速的状态估计仿真结果如图9 和图10 所示。
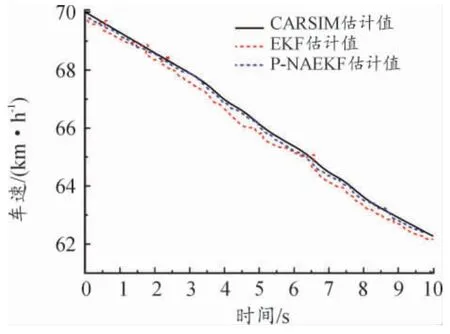
图9 纵向车速曲线
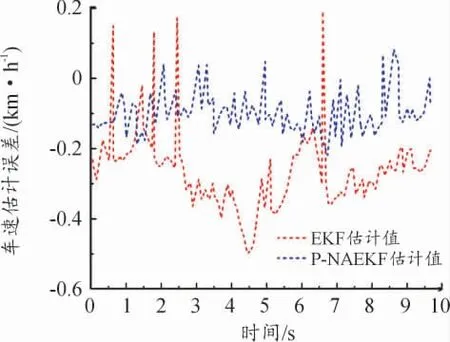
图10 纵向车速滤波偏差曲线
从图9 和图10 可以发现,P-NAEKF 算法的估计效果明显优于EKF,最大误差仅为0.2 m/s,数值波动能够处于稳定状态,且与实际数值接近;而EKF 的最大误差达到了0.5 m/s。
通过传统EKF 算法估计的横摆角速度以及本文提出的P-NAEKF 算法估计的横摆角速度与Carsim 输出参数值进行对比分析。横摆角速度的状态估计仿真结果如图11 和图12 所示。
从图11 和图12 可以发现,P-NAEKF 算法的估计效果明显优于EKF,其估计值一直处于真实值附近,误差很小,而传统的EKF 在某些时刻存在发散现象。

图11 横摆角速度曲线

图12 横摆角速度滤波偏差曲线
通过传统EKF 算法估计的质心侧偏角以及本文提出的P-NAEKF 算法估计的质心侧偏角与Carsim 输出参数值进行对比分析。质心侧偏角状态估计仿真如图13 和图14 所示。
从图13 和图14 可以发现,P-NAEKF 的估计效果大大优于EKF,传统EKF 在10 s 的时间里存在不止一次的发散现象,而P-NAEKF 算法保持较好的收敛性,其估计值位于真实值附近,最大误差仅为0.2°左右,数值波动能够处于稳定状态。

图13 质心侧偏角曲线
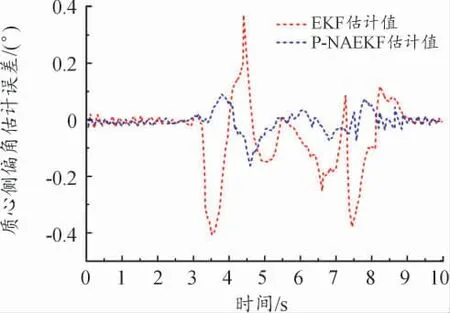
图14 质心侧偏角滤波偏差曲线
根据仿真实验,可以得到:在噪声协方差获取数值不精准的情况下,P-NAEKF 可以通过基于粒子群的参数优化估计方法对噪声协方差进行矫正,因此P-NAEKF 具有优异的估计精度和良好的收敛性,能够较好地解决噪声协方差获取不准确的情况下的车辆行驶状态估计问题。
6 结论
1)构建了基于纵向车速,横摆角速度和质心侧偏角的3 自由度模型,考虑了纵向车速和传统汽车状态参数之间的非线性关系,更严谨地解决汽车状态估计问题。
2)提出了基于粒子群算法的参数优化估计方法,并通过Matlab 仿真与传统的Sage-Husa 算法进行对比,验证了本文提出的参数估计方法的优越性。
3)提出了基于NAEKF 算法的汽车行驶状态估计方法,通过联合仿真验证了该算法在噪声协方差不准确的环境下可以提供更加准确的车辆状态估计。
